多信道有限缓存下混合业务接入控制的排队性能研究
黎锁平 徐倩毓 JAAFAR Gaber
(1.兰州理工大学电气工程与信息工程学院,甘肃兰州 730050;2.兰州理工大学理学院,甘肃兰州 730050;3.Universite de Technologie Belfort-Montbeliard,Belfort 90010,France)
1 引言
通信网络的信道通常是有限的,为了减少通信的受阻和数据的丢失概率,网络会提供一定的缓冲位置.随着通信网的飞速发展,网络拥塞(congestion)现象越来越频繁.随着网络中传输数据分组的增加,有限的节点储存容量易使网络传输性能下降,从而出现数据丢失、时延增加、吞吐量下降等现象,严重时还会导致“拥塞崩溃”(congestion collapse).
网络中每个输出端口有一定的存储空间,若一个输出端口被几个输入数据流共同使用,输入流的数据包就会在该存储空间内排队.当端口转发数据的速率低于数据包的到达速率时,会造成存储空间被占满的情形,从而引起网络拥塞.如遇地震等突发事件,语音通信业务的骤增会导致网络崩溃,引发严重后果.为了方便处理,一般的排队模型通常研究具有无限缓冲器的情况.从某种程度上来讲,存储空间的增加能够缓解输出端口的压力.但存储空间无限制的增加会导致数据包完成转发时就早已超时,而源端认为这些数据包在传输过程中被丢弃而要求重发.这不仅降低网络效率,还会加重网络拥塞.另外在实际应用中,存储容量也不可能无限制的增加.多信道有限缓存的排队系统就是为了研究此种网络拥塞而提出的.
文献[1]中讨论了带有故障的多服务器同构的排队系统,并进行了忙期分析.文献[2]研究了带有止步和中途退出M/M/C/N排队系统,并得到了系统的稳态概率和平均队长.文献[3]研究了两种入口协议下离散时间有限缓存的Geom/Geom/c消失系统,校正了模型的损失率等.文献[4–5]研究了有限缓存下单服务台的排队系统.其中文献[4]讨论了多重休假排队系统,使用嵌入马尔可夫链和补充变量法,得到系统的稳态分布等性能指标并进行了数值检验.文献[5]讨论了服务台串联排队系统,通过分解串联队列为单缓存子系统,得到了系统的吞吐量.文献[6–7]研究了带有休假的有限缓存排队模型.其中文献[7]研究了带有启动时间和可修服务台的M/M/1/N工作休假排队系统.
随着宽带网技术的高速发展,通信网不再局限于服务单一类型的业务.但不同的业务对误码率、时延和抖动等有着不同要求.通信网的业务按传输的实效性可分实时业务(如语音视频等)和非实时业务(如数据等).当信道混合传输两类业务时,为保证通信的及时性,通常认为实时业务的优先权高于非实时业务,并能够抢占非实时业务的信道.
文献[8]研究了节点优先权问题,对不同优先级节点提出了基于DI–RED的排队方案以控制网络拥塞.文献[9–10]研究了两类业务带有优先权的单服务台排队模型.文献[11–12]研究了两类业务带有优先权的多服务台排队模型.其中文献[11]利用连续时间排队得到系统的各项性能指标.
然而,综合考虑有限缓存和优先权的研究还很少(如文献[11]).通信网络中业务传输的最小单位是时隙,但对应的离散时间排队模型由于其理论研究难度更大因此并不够丰富.考虑到带有优先权业务且具有有限缓存的通信网络在生活中随处可见(如移动网络业务等),为丰富其理论研究本文讨论了有限缓存下带有优先权的多服务台排队模型.将业务按实时性和非实时性分为两类,实时性业务具有抢占优先权.并利用离散时间排队方法获得两类业务的稳态概率和性能指标,同时提出了相应的网络拥塞控制策略.
2 系统建模
本文所讨论的是无线通信网络中移动台(mobile station,MS)通过基站(base station,BS)获得多业务服务的离散时间模型.时间轴被分为时隙(slot)相同的间隔,业务到达只能发生在时隙开始,同时业务离去只能发生在时隙结束前,即系统为早到系统.
2.1 有限缓存下优先接入控制机制
假设系统中有s条信道供两类业务共同使用:第1类是时延不敏感业务(如数据业务);第2类是时延敏感业务(如:语音业务).第i类业务的到达率为λi,服务率为µi,(i=1,2).系统的优先接入机制如图1所示,其中第2类业务具有高优先权.
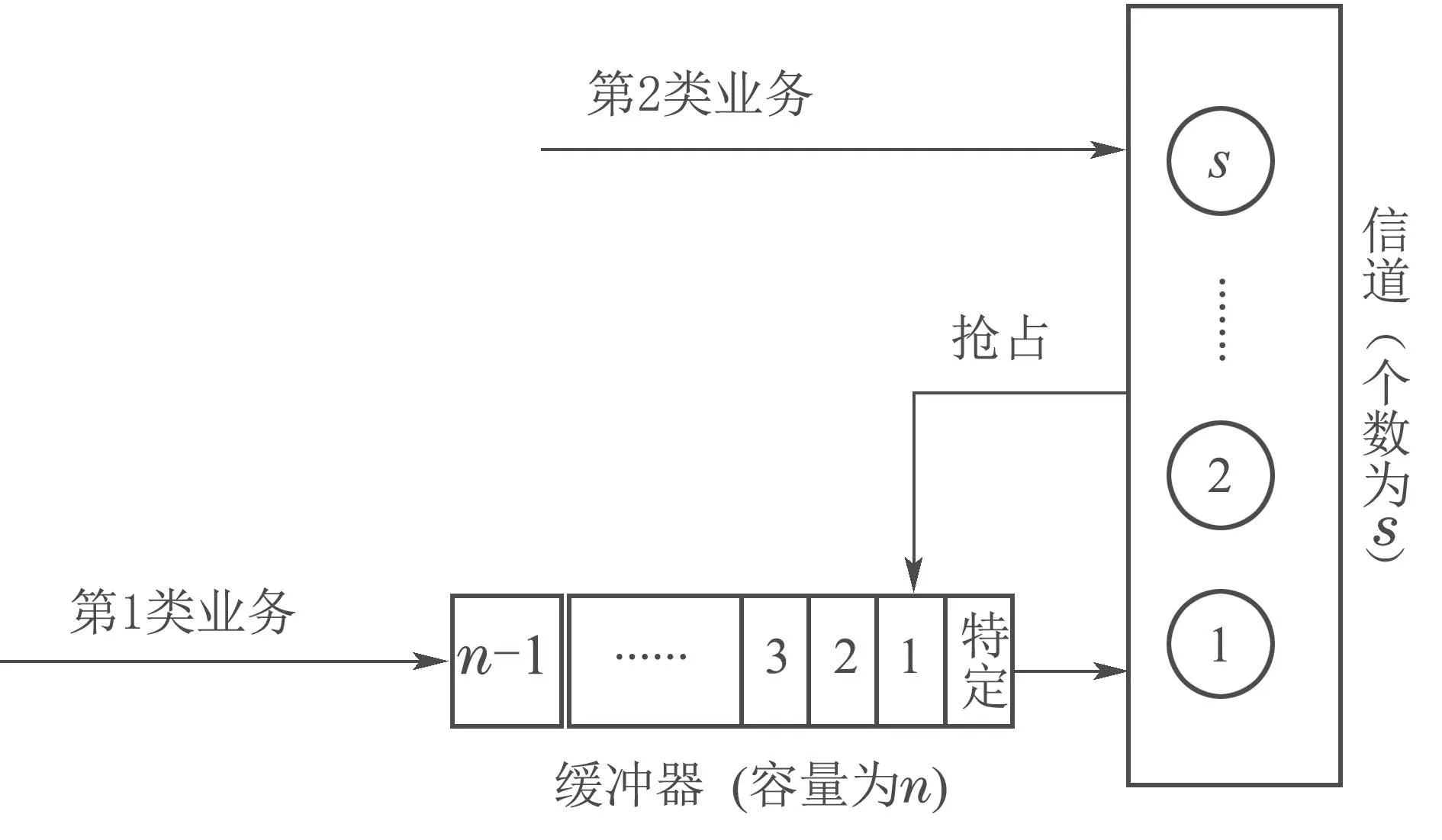
图1 有限缓存下优先接入控制机制Fig.1 Admission control scheme with priority under finite buffer
1) 如果第2类业务到达时所有信道被占用,且一部分信道服务第1类业务,则其中一个信道要立即结束对第1类业务的服务为新到达的第2类业务服务;
2) 如果第2类业务到达时所有的信道均为第2类业务所占用,则第2类到达业务被阻塞;
3) 当缓冲器未满时,刚到达系统且发现所有信道均被占用的第1类业务或者由于优先权而被排挤下来的第1类业务进入缓冲器排队等待服务.
当缓冲器已满且一部分信道服务第1类业务,新到达的第2类业务由于其优先权抢占信道,从而导致被强行终止的第1类业务丢失.为防止此类业务的丢失,本文分出缓冲器(容量为n)的一个存储空间称为特定缓冲器,用于缓存此类业务并排在首位接收信道服务.此时,缓冲器的实际容量缩小为n −1.这种系统被称为有限缓存下混合业务带有优先接入控制的多服务台离散时间排队系统,记为Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s.
2.2 系统状态转移概率矩阵
令L1(k)表示k时刻信道与缓冲器中第1类业务数之和,故L1(k)可取0,1,2,···,n −1+s;L2(k)表示k时刻信道与缓冲器中第2类业务数之和,故L2(k)可取0,1,2,···,s.则Ω={L1(k),L2(k)}是一个二维Markov链,且有状态空间{(i,j);i=0,1,2,···,n −1+s,j=1,2,···,s}.符号={(i,0),(i,1),···,(i,j),···,(i,s)}表示i水平,j称为系统的位相.系统的状态空间被分块成水平集,每个水平都有s+1个位相.系统运行可分为5种状态:
状态I(空闲状态):s条信道中全部或有一部分信道空闲,新进入的两类业务都可进入信道;
状态II(优先状态):s条信道都被占用且缓冲器未满,但系统中第2类业务数小于s,新进入的第2类业务抢占信道,因优先权而被排挤下来的第1类业务进入缓冲器的队首排队等待服务,新进入的第1类业务进入缓冲器等待服务;
状态III(阻塞状态1):s条信道都为第2类业务服务且缓冲器未满,即j=s.新进入的第2类业务被阻塞,而新进入的第1类业务进入缓冲器等待服务;
状态IV(阻塞状态2):s条信道都被占用且缓冲器已满,但系统中第2类业务数小于s,新进入的第2类业务抢占信道,因优先权而被排挤下来的第1类业务进入特定缓冲器,排在队首位置等待服务;
用s+1阶主对角阵Di,j=P{L1(k)=j|L1(k −1)=i}=diag{d0,d1,···,ds}表示第2类业务数为0,1,2,···,s下第1类业务个数从i转移到j的概率,则


Di,j的具体形式由以下4个定理给出:
定理1Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s系统中,
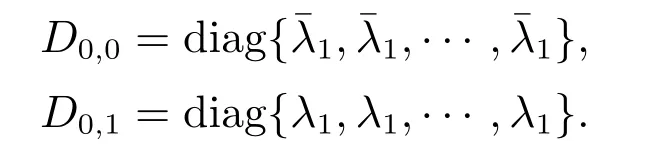
证当信道中分别有0,1,2,···,s个第2类业务时,第1类业务数从0个转移到0个,则
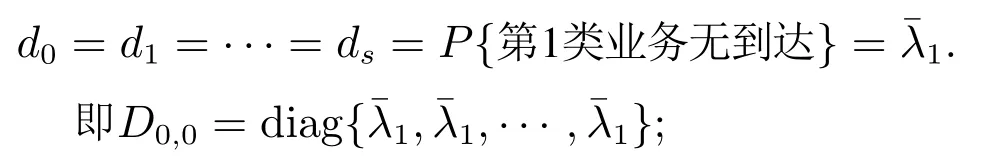
当信道中分别有0,1,2,···,s −1个第2类业务时,第1类业务数从0转移到1,此时

即D0,1=diag{λ1,λ1,···,λ1}. 证毕.
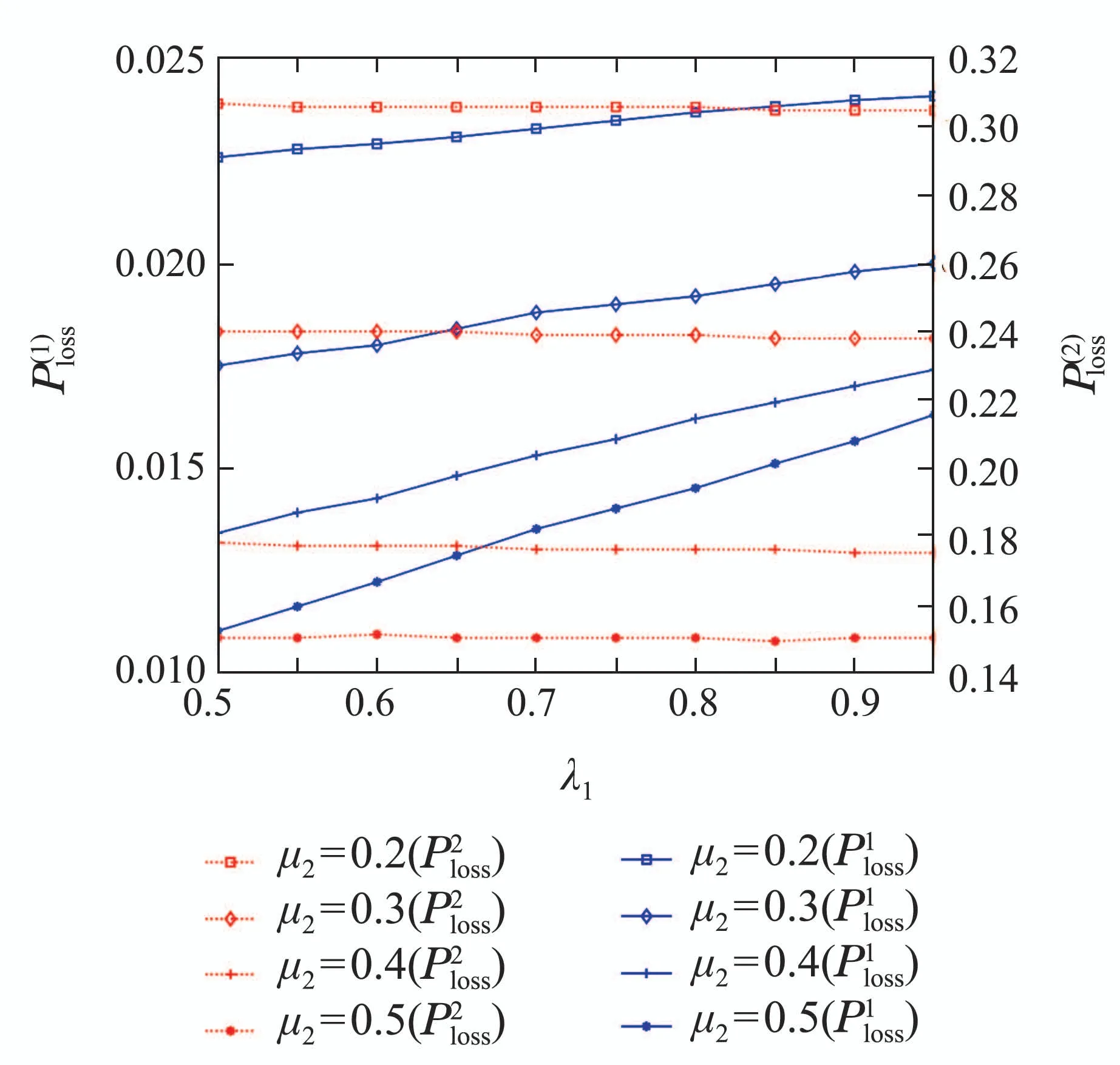
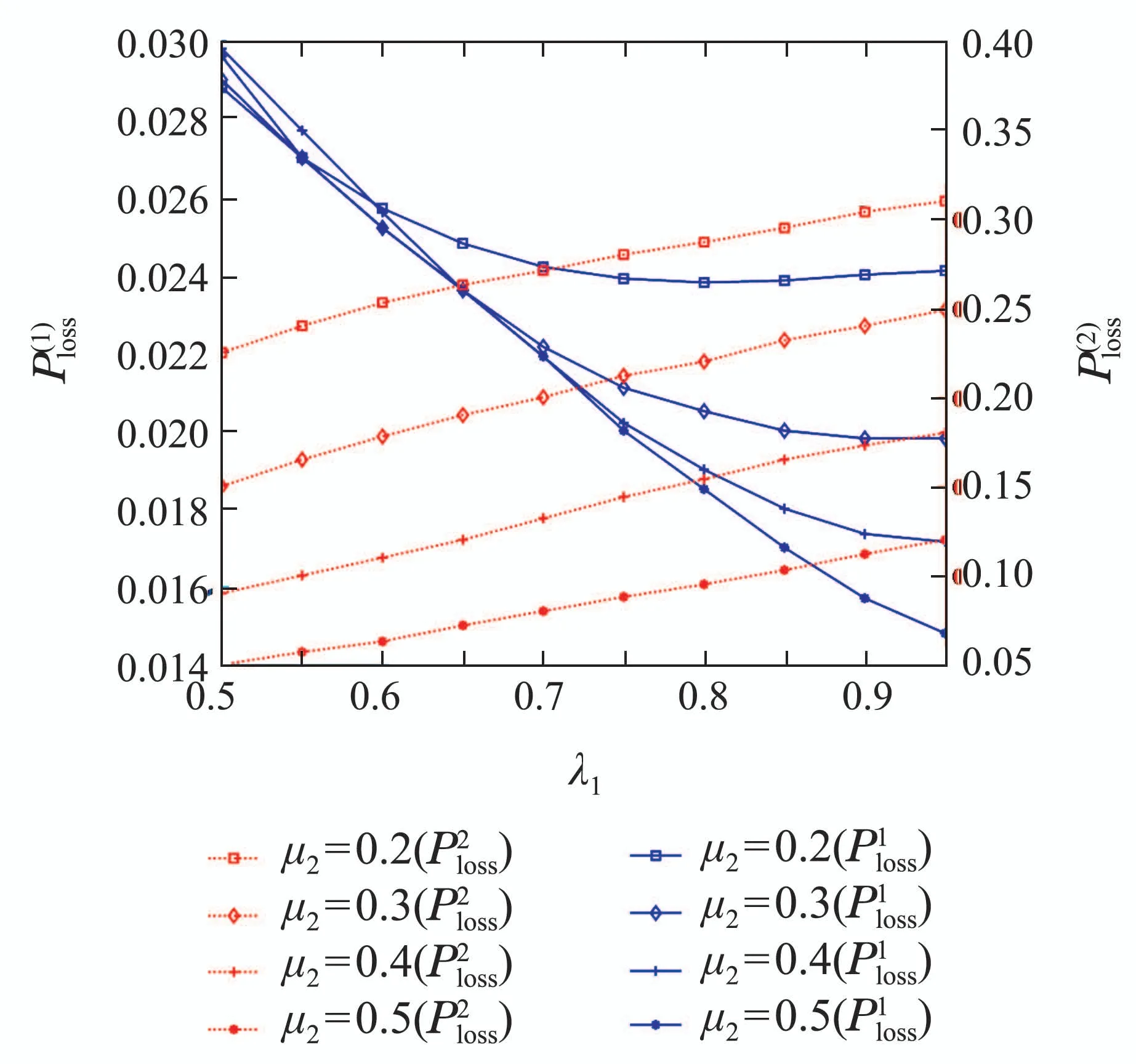
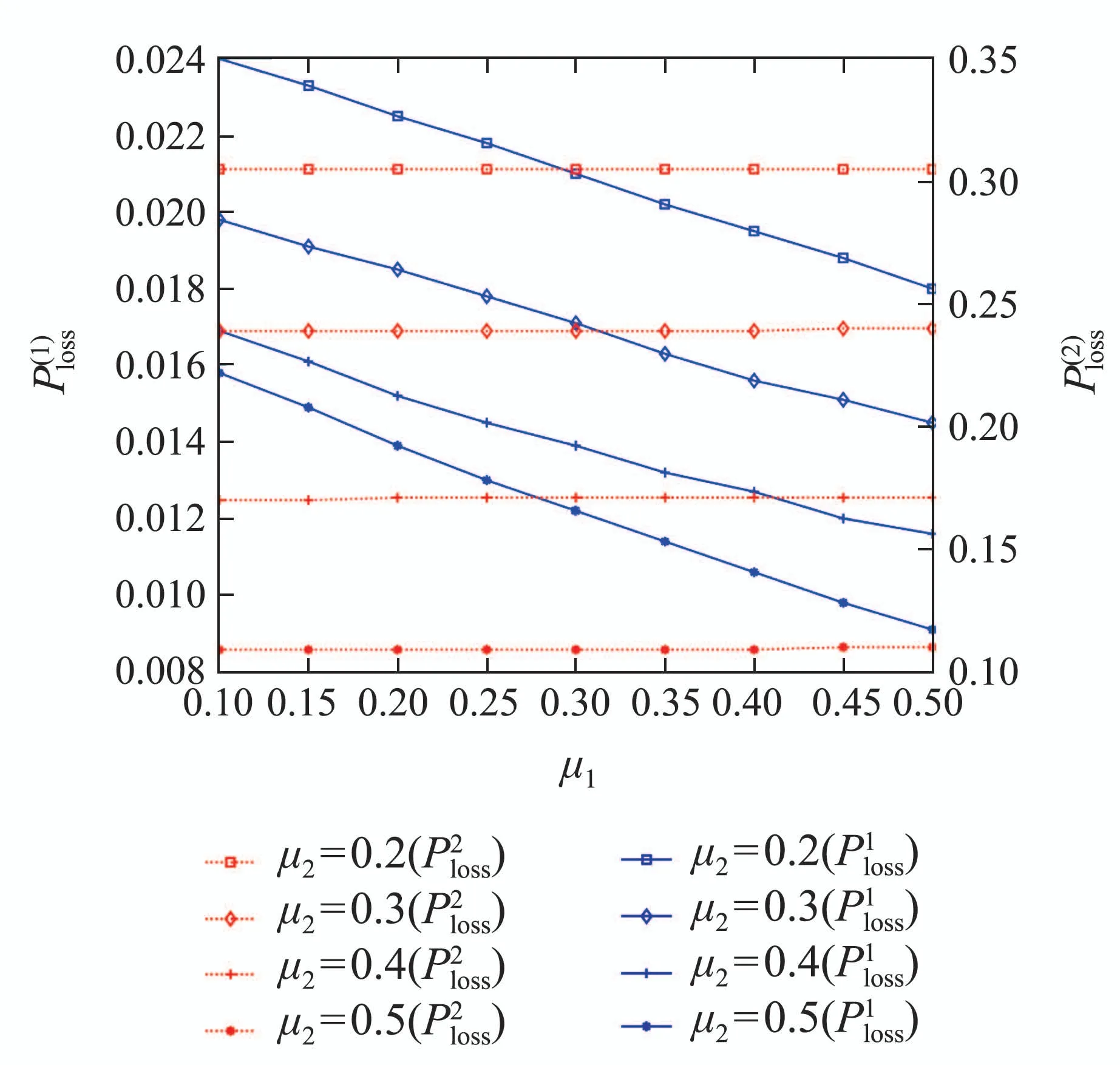
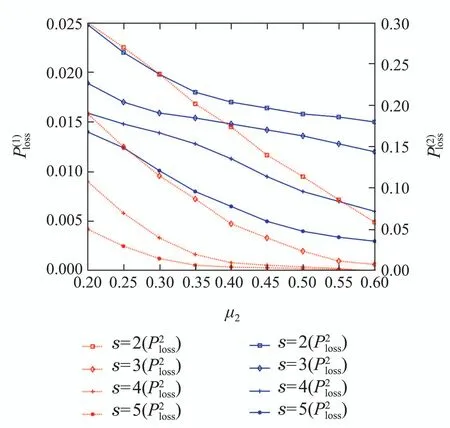
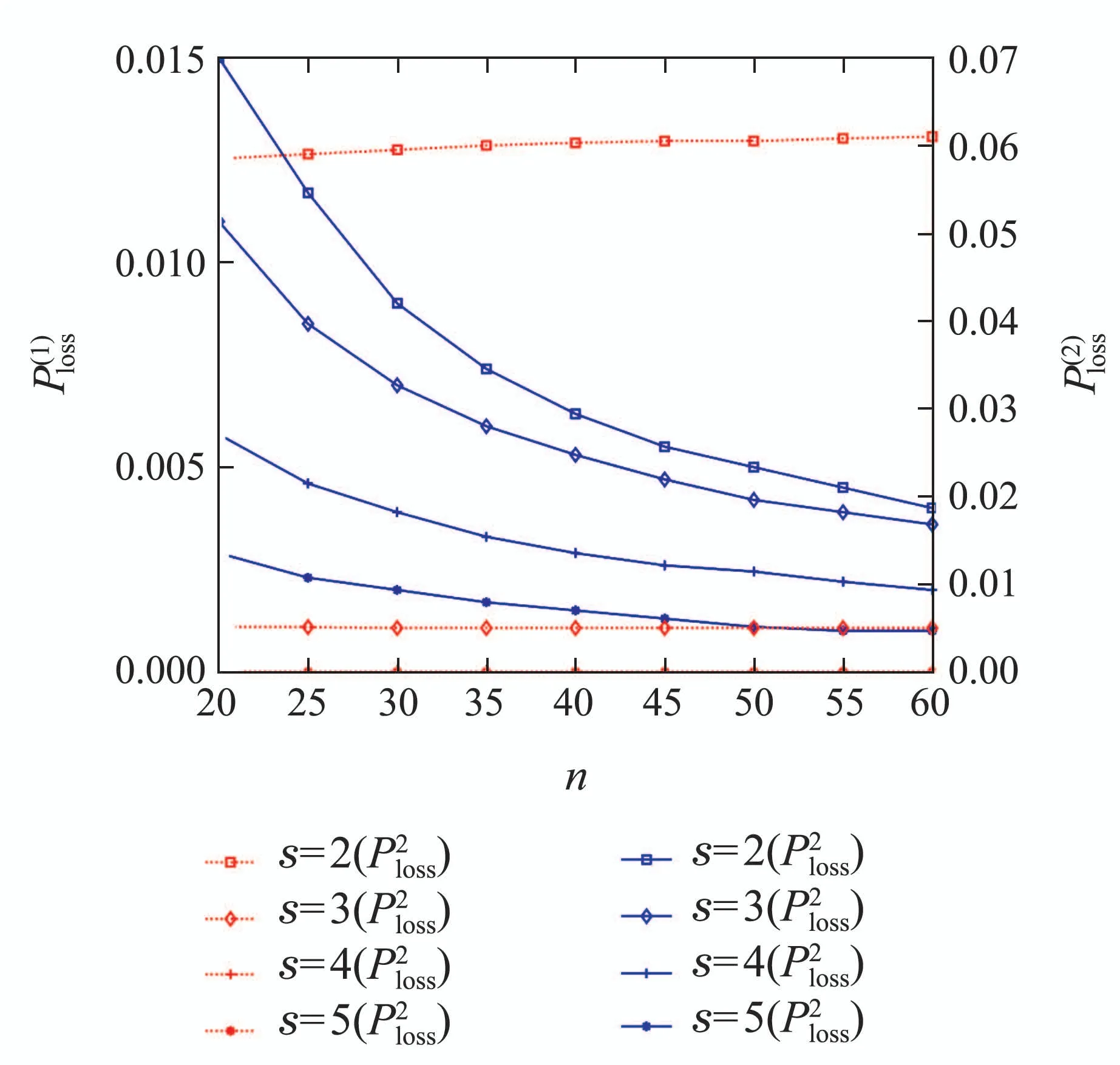
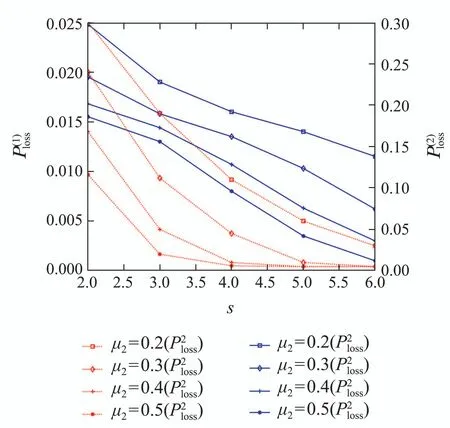
定理2Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s系统中,当1 ≤i 证1) 若第1类业务数从i转移到0,则第2类业务可 能 有0,1,2,···,s −i个,因 此,d0=d1=···=ds−i=.即 其中D表示曲线的波动偏差,len(S)表示散射参数曲线中散射参数的数量.Fi表示滤波后第i个散射参数的幅值,Si表示样本原始点所对应的幅值. 2) 若第1类业务数从i个转移到j个,当信道中分别有0,1,2,···,s −i个第2类业务时,i个第1类业务都在信道中,则 已知s+1阶主对角阵Di,j=P{L1(k)=j|L1(k−1)=i}=diag{d0,d1,···,ds}表示第2类业务数为0,1,2,···,s下第1类业务个数从i转移到j的转移概率,根据i的不同取值,得到了Di.j的通项表达式(见定理1–4).令 表示第1类业务数从i个转移到j个,同时第2类业务数从0,1,2,···,s到0,1,2,···,s共(s+1)×(s+1)种转移情况的联合概率矩阵,其中 同理可得矩阵P=(Pi,j)(n+s)×(n+s)表示共(n+s)×(n+s)×(s+1)×(s+1)种转移情况的联合概率. 证毕. 引理1有限状态不可约非周期Markov链正常返的充分必要条件是存在自然数n,使n阶转移概率阵无零元素[14]. 定理6当0<λ1,λ2<1,0<µ1,µ2<1时,Ω={L1(k),L2(k)}是一个正则Markov链. 证Ω中所有状态是互通的,故Markov链是有限、不可约的.由P=(Pi,j)(n+s)×(n+s)知Markov链是非周期的,由引理1易验证这是一个正常返的Markov链,故为正则Markov链. 证毕. 一个正则Markov过程存在唯一的平稳过程,以L1,L2表示系统中两类业务队长{L1(k),L2(k),k≥0}的稳态极限,稳态分布记为 其中:πi=(πi0,πi1,πi2,···,πis)⊥表示第1类业务个数为i的稳态概率, 表示第1类业务个数为i且第2类业务个数为j的稳态概率,从而稳态分布满足平衡方程:πP=π,πe=1, 其中Pi,j为s+1阶方阵.求解方程可确定稳态分布π. 1) 平衡条件下系统中第1类业务数的平稳概率分布为 其中e为s+1阶全1列向量.则系统中第1类业务的平均队长 因此,Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s系统中,第1类业务的损失率为 2) 平衡条件下系统中第2类业务数的平稳概率分布为 则系统中第2类业务的平均队长是 因此,Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s系统中,第2类业务的损失率为 以无线通信系统中基站(BS)的上行信道为例.假设系统中有语音和数据两类业务,语音业务具有抢占优先权;信道个数为2,3,4,5,6;数据业务到达率λ1为0.5∼1.0;语音业务到达率λ2为0.5∼1.0;数据业务服务率µ1为0.5∼1.0;语音业务服务率µ2为0.2∼0.6;通过以上参数的设定,结合式(1)(2)(4)(6)可得到两类业务的损失率. 图2为数据业务的到达率λ1与数据业务损失率和语音业务的损失率之间的关系.从左边y轴可以看出,数据业务的损失随着数据业务到达率的增加而上升,随语音业务服务率的增加而降低.同时由曲线的变化趋势可得,语音业务服务率越高,数据业务的损失率随数据业务到达率的变化越快.由4条曲线的间距可得,当语音业务服务率等间距增大时,数据业务的损失率并不是等间距减小的,其减小的间距越来越小.从右边y轴可以看出,语音业务的损失率的每条曲线接近于常值曲线,可得语音业务的损失率几乎不受数据业务到达率的影响.但会随着语音业务服务率的增加而降低.由曲线间距可得,当语音业务服务率等间距增大时,语音业务的损失率也是等间距减小的.即语言业务的损失率与语音业务的服务率呈线性关系. 图2 数据用户到达率(λ1)与数据/语音用户损失率的关系Fig.2 Relationship between arrival rate of data user(λ1)and packet loss rate of data/voice user 图3为语音业务的到达率λ2与数据业务损失率和语音业务的损失率之间的关系.从左边y轴可以看出,数据业务的损失率分别随语音业务到达率和语音业务服务率的增加而降低.当语音业务服务率等间距增加时,数据业务的损失率起初随语音业务到达率增大的趋势不大,但当语音业务到达率超过0.6后,这一趋势越来越大.从图上可以看出,语音业务服务率为0.5时,数据业务的损失率几乎随语音业务到达率的增加而线性递减.所以提高语音业务服务率可以有效降低数据业务损失率.从右边y轴可以看出,语音业务的损失率随语音业务到达率的增加而上升,随语音业务服务率的增加而降低.当语音业务费率等间距增大时,语音业务损失率减小的间距越来越小. 图3 语音用户到达率(λ2)与数据/语音用户损失率的关系Fig.3 Relationship between arrival rate of voice user(λ2)and packet loss rate of data/voice user 图4为数据业务的服务率µ1与数据业务损失率和语音业务的损失率之间的关系.从左边y轴可以看出,数据业务的损失率分别随数据业务服务率和语音业务服务率的增加而降低.当数据业务的服务率µ1为定值时,语音业务服务率等间距增大.数据业务的损失率并不是等间距减小的,其减小的间距越来越小.从右边y轴可以看出,语音业务的损失率几乎不受数据业务服务率的影响.但会随着语音业务服务率的增加而降低.当语音业务服务率等间距增大时,数据业务的损失率也是等间距减小的. 图4 数据用户服务率(µ1)与数据/语音用户损失率的关系Fig.4 Relationship between service rate of data user(µ1)and packet loss rate of data/voice user 图5为语音业务的服务率µ2与数据业务损失率和语音业务的损失率之间的关系.观察左边y轴可得数据业务的损失随着语音业务服务率的增加而降低.4条曲线对应着不同的信道个数,可得数据业务的损失随着信道个数的增加而降低.从右边y轴可以看出,语音业务的损失率分别随着语音业务服务率和信道个数的增加而降低.当信道个数等间距增大时,语音业务的损失率并不是等间距减小的,其减小的间距越来越小.即无限制的增加信道个数,对降低语音业务损失率的显著性会越来越弱. 图5 语音用户服务率(µ2)与数据/语音用户损失率的关系Fig.5 Relationship between service rate of voice user(µ2)and packet loss rate of data/voice user 图6为缓冲器容量n与数据业务损失率和语音业务损失率之间的关系.从左边y轴可以看出,数据业务的损失率分别随着缓冲器容量和信道个数的增加而降低.当缓冲器容量n为定值时,无限制的增加信道容量,对降低数据业务损失率的显著性会越来越弱.从右边y轴可以看出,语音业务的损失几乎不受缓冲器容量的影响.但语音业务的损失会随着信道个数的增加而降低.当信道个数等间距增大时,易得无限制的增加信道个数,对降低语音业务损失率的显著性会越来越弱. 图6 缓冲器容量(n)与数据/语音用户损失率的关系Fig.6 Relationship between buffer capacity (n) and packet loss rate of data/voice user 图7为信道个数s与数据业务损失率和语音业务损失率之间之间的关系.从图中可以看出数据业务的损失率分别随着信道个数和语音业务服务率的增加而降低,语音业务的损失率分别随着信道个数和语音业务服务率的增加而降低. 图7 信道个数(s)与数据/语音用户损失率的关系Fig.7 Relationship between channel number (s) and packet loss rate of data/voice user 从图示结果得到以下重要结论: 1) 增加信道个数可以有效地降低两类业务的损失率,这与控制网络拥塞时的经验方法一致,即本文给出了控制网络拥塞时的经验方法的理论依据; 2) 无限制的增加信道个数,对降低两类业务损失率的显著性会越来越弱.即信道个数增加的越多,经济成本越来越大,但是对控制网络拥塞的效果却越来越差.故在实际控制网络拥塞时不建议无限制的增加信道个数. 3) 提高优先级业务的服务率可以有效地降低两类业务的损失率. 据此本文对控制网络拥塞提出改进措施,因为无限制的增加信道个数却不能有效降低两类业务的损失,故建议选择经济成本相对节约的信道个数,努力提高优先级业务的处理效率.比如地震发生后,提醒语音用户通话时间不能超过1分钟只需交流重要信息,通过限制语音用户的通信时间从而使其快速离开信道,保证更多的语音用户进入信道,从而达到控制网络拥塞的目的. 本文对有限缓存下混合业务带有优先接入控制的多服务台离散时间排队系统Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s进行数学建模,得到两类业务的稳态分布、平均队长、损失率,以及信道的平均利用率等主要性能指标.最后,对所建模型进行数值模拟,得到各业务到达率、服务率、信道个数、缓冲器容量与各业务损失率的关系.针对网络拥塞控制,本文提出可以通过增加信道个数、提高优先级业务的服务率有效地降低两类业务的损失率.不仅给出了Geom1±Geom2/Geom1,Geom2/s,s(PP)/n+s,s,离散时间系统下网络拥塞的理论支撑,丰富和完善经典排队论的理论体系,而且对网络拥塞控制提出建议,对优化和设计网络拥塞控制具有良好的指导意义.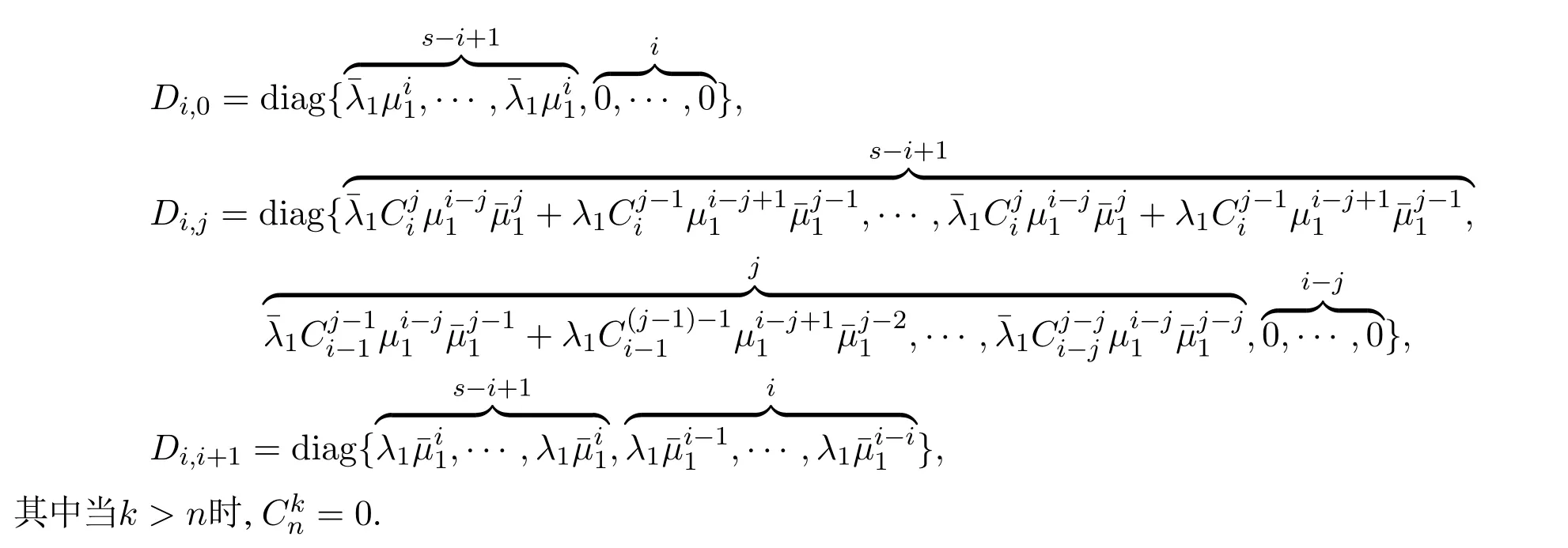
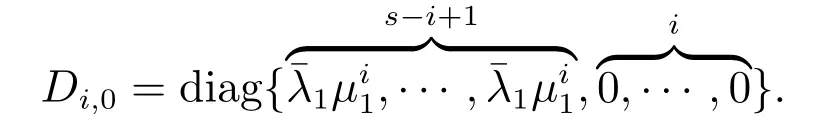
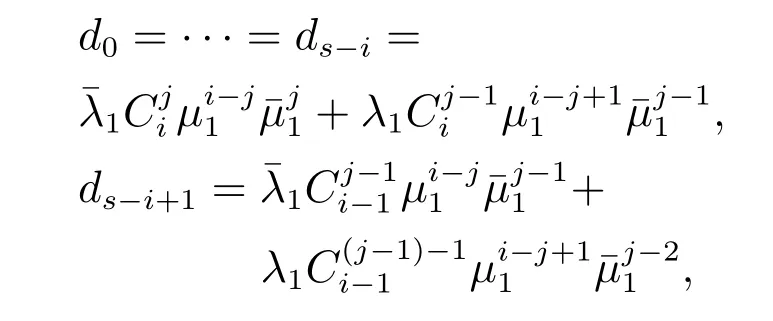


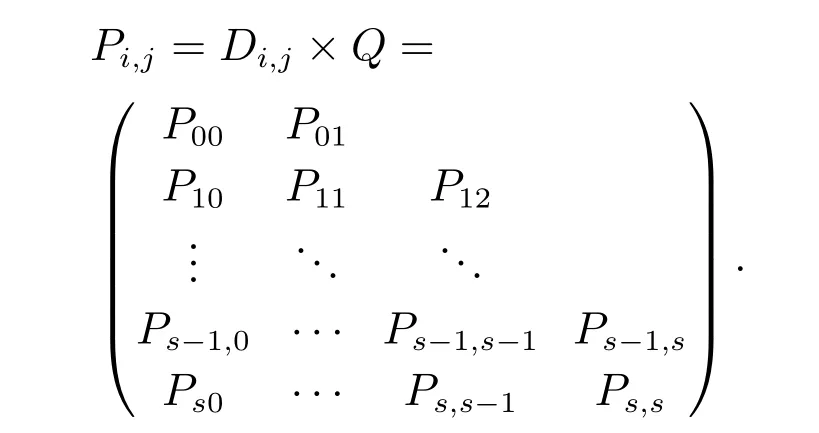
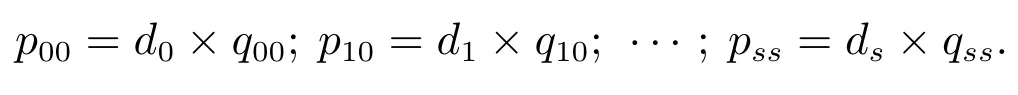
2.3 系统稳态概率分布
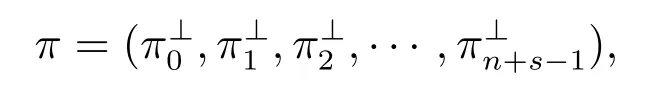
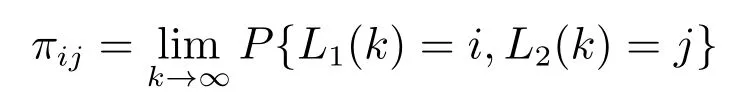

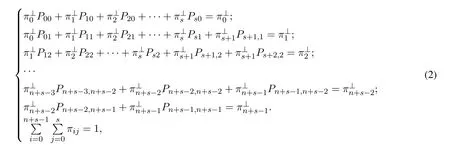
3 系统性能指标分析
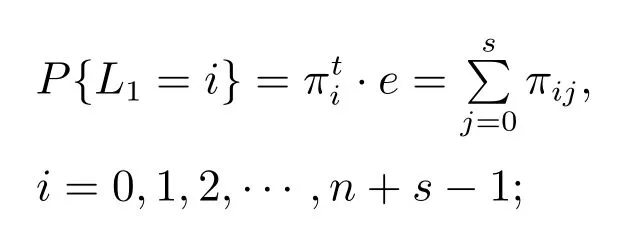
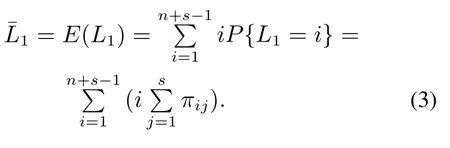
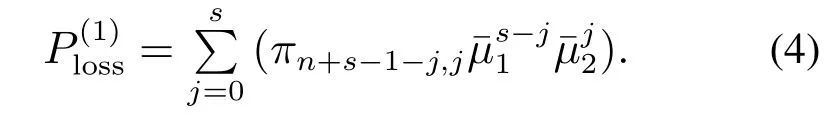
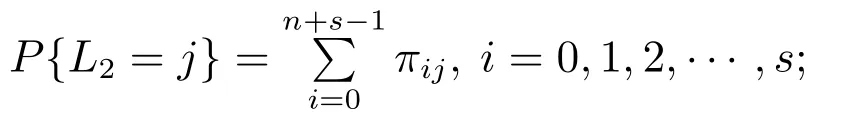
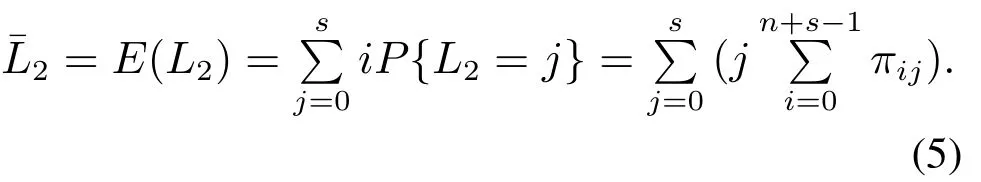
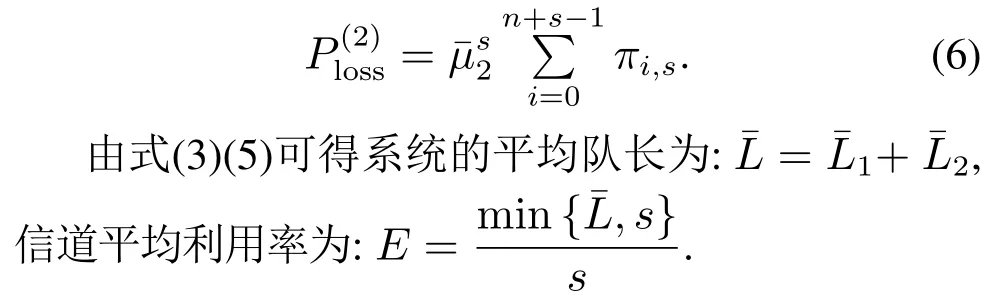
4 数值结果与仿真分析
5 结论

