六步法在二次函数图像教学中的应用

李家燕

【摘要】六步法能够有效提升初中数学二次函数的教学水平，提升初中数学教学的整体质量，培养学生的数学思维，促进学生的进一步成长.学生通过六步法能够有效解决二次函数图像与解析式转化的难题.

【关键词】二次函数;图像教学;六步法

1 六步法及其在初中二次函数图像教学中的应用价值

在进行函数图像解析时可以采用六步法，打破传统图像教学中先列表后画图的方法，更好更有效地解决二次函数取值的问题.二次函数图像教学中采用六步法也能够让学生更好地掌握二次函数的变换规律，有助于学生夯实二次函数知识，形成数形结合的知识体系.

2 例题分析

2.1 二次函数y=ax2的图像

二次函数y=ax2图像的教学难点重点在于选择合适的自变量值与相应函数值来进行函数图像的绘画.具体操作中需要考虑到第一个值应该选多大，接下来几个该如何选，将这些值从小到大进行排列，相邻两组的值间距应当取多少？取多少个值才能够画出整个图像？这些都需要学生对解析式的特征进行分析，对取值的可行性进行分析判断.学生进行取值时，教师应当引导学生通过值与点对应函数图像进行画图，采用六步法来分析y=ax2型二次函数的图像（图1所示），采用数形结合的方式来画函数图像.

学生可以在坐标系中进行自由发挥，通过计算各组的x，y对应值，在坐标图中进行定点.对取点位置采取开放不设定限制的形式，学生通过这样的方法能够总结出如何用最便捷的方法进行取点，能够更加容易定点.同时也会总结出通过取整计算的点定的越多就越准确.x值取最小绝对值，大多数学生都能够画出二次函数y=x2的对称点和顶点，通过画图来发现图像的对称特点.

学生在画图过程中遇到的难点是当（2，4）和（3，9）这两点的距离较远时，无法清晰判断点在这两点之间的走向，进行各个点连接时就存在一定难度.教师可以引导学生进行讨论，在这两点之间尝试取（2.5，6.25），也可以尝试在（3，9）和（4，16）两点间取（3.5，12.25），以此类推，根据题型需要选取中间位置的点，有助于判断点的走向.学生在进行顶点和相邻两点连接时常会选择用线段进行连接，教师可以引导学生在这两点之间取（0.5，0.25）试试.学生通过计算定出9个或者9个以上的点，进行归纳和推理能够得到一条曲线，证明二次函数的图像是一条光滑的抛物线.

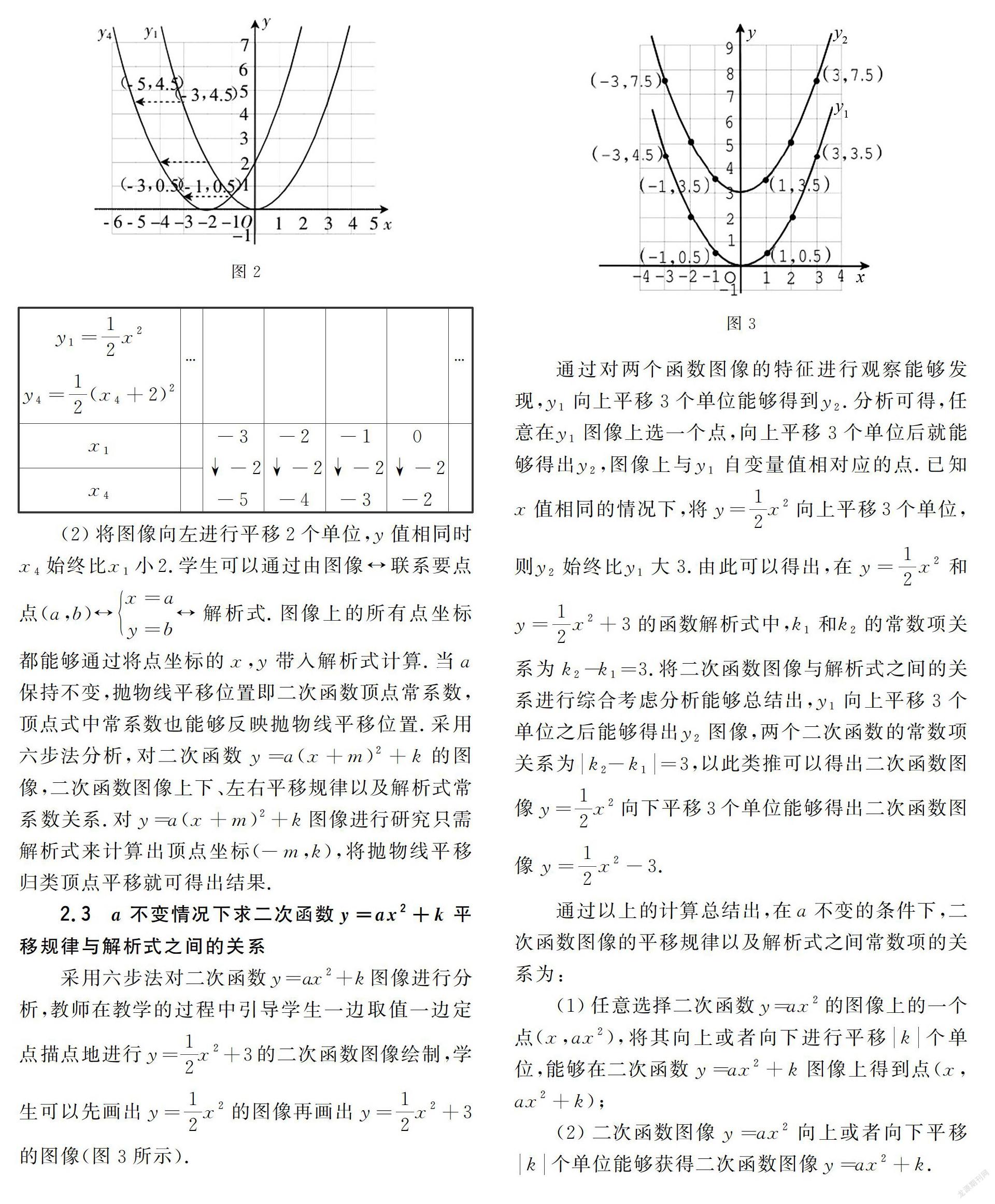
2.2 二次函数y=a（x+m）2的图像

与图像上下平移的规律进行对比后能够得出图像左右平移的规律，总结出解析式常系数之间的关系，进而画出y4=12（x+2）2的图像.左右平移规律与上下平移规律进行对比后能够总结出几点不同之处：

（1）画函数y4=12（x+2）2的图像时，教师引导学生对图形进行补全（图2所示）.

y1=12x2

y4=12（x4+2）2

…

…

x1

x4

-3

↓-2

-5

-2

↓-2

-4

-1

↓-2

-3

0

↓-2

-2

（2）将图像向左进行平移2个单位，y值相同时x4始终比x1小2.学生可以通过由图像联系要点点（a，b）x=ay=b解析式.图像上的所有点坐标都能够通过将点坐标的x，y带入解析式计算.当a保持不变，抛物线平移位置即二次函数顶点常系数，顶点式中常系数也能够反映抛物线平移位置.采用六步法分析，对二次函数y=a（x+m）2+k的图像，二次函数图像上下、左右平移规律以及解析式常系数关系.对y=a（x+m）2+k图像进行研究只需解析式来计算出顶点坐标（-m，k），将抛物线平移归类顶点平移就可得出结果.

2.3 a不变情况下求二次函数y=ax2+k平移规律与解析式之间的关系

采用六步法对二次函数y=ax2+k图像进行分析，教师在教学的过程中引导学生一边取值一边定点描点地进行y=12x2+3的二次函数图像绘制，学生可以先画出y=12x2的图像再画出y=12x2+3的图像（图3所示）.

通過对两个函数图像的特征进行观察能够发现，y1向上平移3个单位能够得到y2.分析可得，任意在y1图像上选一个点，向上平移3个单位后就能够得出y2，图像上与y1自变量值相对应的点.已知x值相同的情况下，将y=12x2向上平移3个单位，则y2始终比y1大3.由此可以得出，在y=12x2和y=12x2+3的函数解析式中，k1和k2的常数项关系为 k2-k1=3.将二次函数图像与解析式之间的关系进行综合考虑分析能够总结出，y1向上平移3个单位之后能够得出y2图像，两个二次函数的常数项关系为k2-k1=3，以此类推可以得出二次函数图像y=12x2向下平移3个单位能够得出二次函数图像y=12x2-3.

通过以上的计算总结出，在a不变的条件下，二次函数图像的平移规律以及解析式之间常数项的关系为：

（1）任意选择二次函数y=ax2的图像上的一个点（x，ax2），将其向上或者向下进行平移k个单位，能够在二次函数y=ax2+k图像上得到点（x，ax2+k）;

（2）二次函数图像y=ax2向上或者向下平移k个单位能够获得二次函数图像y=ax2+k.