APOS理论下的高三立体几何复习建议

王娜

【摘 要】 APOS理论最早是由杜宾斯基提出的，是一种科学的建构主义理论，这种理论强调了个人的重要性，个人想要得到结果，需要以旁观者的角色参与到活动中，能总结和反思活动的方法、内容、过程.在参与的过程中，能充分发挥自身的创造力，还能展现主观能动性.这可看出，APOS理论充分体现了学生在学习过程中的主体性，说明学习过程是在经历充分的总结和反思之后的结果.数学学习的重要方式和途径是个体能够在活动中有所经历，通过图式阶段、对象阶段来建构概念，在这其中，个体会产生抽象的思维，能够主动反思该階段学习的过程、方法，会意识到反思的重要性. 本文以高三立体几何复习为例，分析APOS理论在数学教学中的应用.

【关键词】 APOS理论;立体几何;高三数学

1 立体几何复习背景分析

高三的学生已经在高二完成了立体几何的学习，根据北京高考的实际情况，所有学生都学习了空间几何体、空间点线面的位置关系以及利用空间向量解决立体几何的问题.到了高三，师生们更多地关注了利用空间向量解决问题，而忽略了对学生空间想象能力的进一步培养.但是很多研究表明，学习立体几何应重在培养学生的空间想象能力，所以，在高三立体几何的复习过程中，还是要关注学生对于图形的再认识，对于点线面关系的综合认识，而后再利用空间向量作为工具来验证结论，通过“实践—反思—提炼—再实践”的学习方式，利用APOS引导学生进行有效的学习，提高学生的直观想象和逻辑推理能力.

2 “活动（Action）阶段”一一建构直观想象能力的起点

APOS理论的活动阶段是指教师根据学生已有的知识经验，合理地为学生提供感性素材，刺激他们的视觉和听觉，并对其进行感知和转换，在这里，“活动”不仅包括可看见的行为，还包括一些隐性的、能激发学生思维的活动.

在高三立体几何的复习过程中，让学生再一次重现认识的基本图形，在图形中发现并应用空间几何体点线面的位置关系或者空间向量来验证结论，这个过程就是抽象思维的操作过程.

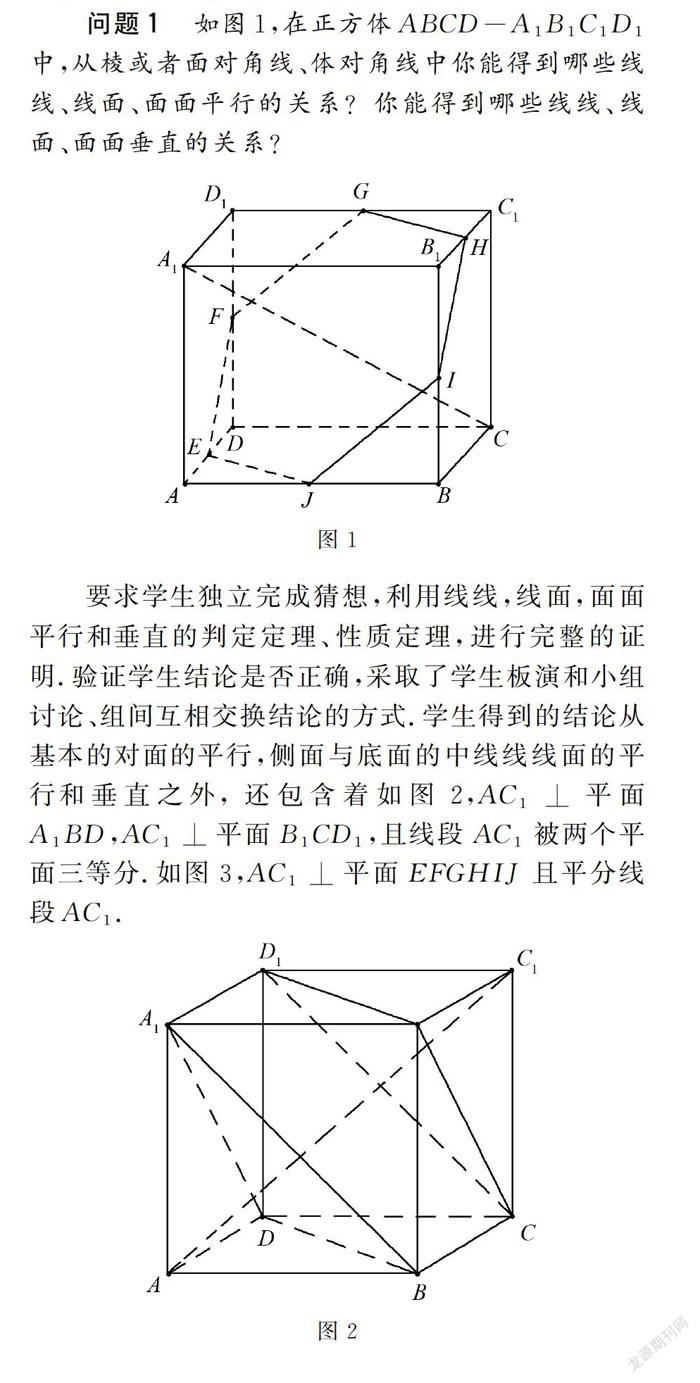
问题1 如图1，在正方体ABCD-A1B1C1D1中，从棱或者面对角线、体对角线中你能得到哪些线线、线面、面面平行的关系？你能得到哪些线线、线面、面面垂直的关系？

要求学生独立完成猜想，利用线线，线面，面面平行和垂直的判定定理、性质定理，进行完整的证明.验证学生结论是否正确，采取了学生板演和小组讨论、组间互相交换结论的方式.学生得到的结论从基本的对面的平行，侧面与底面的中线线线面的平行和垂直之外，还包含着如图2，AC1⊥平面A1BD，AC1⊥平面B1CD1，且线段AC1被两个平面三等分.如图3，AC1⊥平面EFGHIJ且平分线段AC1.

问题的设计，使学生在“活动”阶段感知到了线线线面的平行和垂直，从而将学过的定理定义再现，并且进行互相转化证明直观感知到的结论.通过感知和证明的过程使学生把接触到的数学对象通过一步步的外显性操作指令进行转换，这样有助于学生加深对立体几何整体性的把握.

3 “过程（Process）阶段”一一对于直观感知的反思和总结

APOS理论的“过程阶段”指的是同学们在真实的操作中会初步、直观地感知概念，这能让他们燃起学习的热情，他们会有强烈的学习动机.过程阶段也是整理、分析、处理感性材料的阶段，在这个阶段中，学生会经历联想、想象、观察等过程，会对所学的知识进行思考、总结、分析，将知识内化.这需要学生展示思考的过程，才能实现对问题的总体认识和反思.

问题2 如图4，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F.则下列命题中假命题是（  ）

（A）存在点E，使得A1C1//平面BED1F.

（B）存在点E，使得B1D⊥平面BED1F.

（C）对于任意的点E，平面A1C1D⊥平面BED1F.

（D）对于任意的点E，四棱锥B1-BED1F的体积均不变.

对于问题2，利用问题1的结论，可以很快判断出A，C，D是正确的，但是要求学生写出严格的证明.尤其对于选项B，可以利用反证法，假设B1D⊥平面BED1F，从而推导出B1D⊥BD1而与题目的条件产生了矛盾.

问题3 如图5，在正方体ABCD-A1B1C1D1中，若点P（异于点B）是棱上一点，则满足BP与AC1所成的角为45°的点P的个数为

对于问题3，方法1：利用问题1结论构造各棱顶点与直线AC1所成的角与450相比较，可以发现只有B1C1，C1C，C1D1上存在点P.方法2：应用空间向量设出点P在各个棱上的点坐标，利用两条直线所成角，确定点P的位置.方法3：延长D1A1到点E，使得

D1A1=A1E，由此BE//CA1，所以，点P的轨迹在以点B为顶点，BE为轴顶角为π2的圆锥底面上.通过观察图形，可以发现圆锥只与B1C1，C1C，C1D1相交，故存在点P.

类似利用问题1的一些结论，可以快速的解决正方体中的一些结论，解决问题的“过程阶段”是学生对问题1的操作活动进行反思和总结，通过观察图形、迁移到相似图形、进行判断，证明和总结等过程，对于立体几何的知识内容不断内化和压缩，抽象解决立体几何的基本方法.

4 “对象（Object）阶段”一一学习的整合阶段

APOS理论的“对象阶段”是经过上面两个阶段的学习后，学生能够在学习中形成整体思维，会独立思考问题，成为相对独立的个性，会运用整合、归纳、分析等思维让两个概念之间产生联系但又相互独立.[4]在学习立体几何时，学生要对研究的立体几何对象进行直观感知之后的自然语言、图形语言、符号语言之间的相互转换.

问题4 如图6，四棱锥P-ABCD中，AB∥CD，AB=2CD，E为PB的中点.

求证：CE//平面PAD

问题4的解决是在前两个阶段的学习之上，让学生熟练灵活应用立体几何的知识来解决问题.但是在这个过程中要揭示线面平行本质，是要找寻平面PAD内的一条直线与CE平行，这条直线是过CE的平面与平面PAD的交线.这就涉及到了平面确定的问题，不共线的三点确定一个平面，两条平行线确定一个平面.在图6上我们可以发现直线DF与直线CE构成了一个平行四边形，确定了一个平面，DF就是我们所寻找的交线.同理，在直线AB上任取一点G，点G在平面PAB和平面ABCD的交线上，由此EG与AP交于点K，CG与AD交于点H，HK是平面ECG与平面PAD的交线.通过引导学生确定平面，可以在平面PAD找到很多条符合条件的直线.在这个分析，总结，归纳过程中，既让学生应用了立体几何的基本知识，也给学生建立了如何解决问题的基本思路，培养了学生逻辑推理素养.在这基础之上，继续追问学生平面PAB與平面PCD的交线在哪里？与直线AD是什么位置关系？学生既可以利用刚刚应用的线线平行，线面平行的定理，也可以发现点P可以看成正方体ABCD-A1B1C1D1中，平面A1B1C1D1上任意一点，如图7，会很快找到交线的位置.当然还可以继续在正方体中进行割补找寻更多的位置关系.

以问题4为例，对象阶段学生已经不需要进行对具体问题过程的步骤进行具体分析了，而是将研究问题的整个“过程”看作一个整体，把在“过程阶段”得出的立体几何的线线、线面、面面平行结论进行分析和抽象，从而帮助学生体会立体几何平行问题的本质，和学生共同讨论和总结平行问题的解决方法，给出具体的明确的解决方案，才能形成完整的对象阶段.所以，对象阶段强调的是学生对一类问题的理解和总结并形成具体方案.从“过程阶段”过渡到“对象阶段”是需要学生从对具体的每一个问题的反思，总结，将这类问题进行归纳，建构系统的过程由过程，需要在教师的指导下，学生需要进行不断地反思、总结，抽象，的过程.对于立体几何中垂直关系的教学也可以这样完成.

5 结语

总之，数学的学习是需要经历“实践—反思—提炼—再实践”的过程的，这个过程与APOS理论的四个过程相吻合，所以在数学教学上应用APOS理论，使学生在学习中经历螺旋式的建构过程，对于学生的数学素养的形成有一定的帮助.在今后的实践中，笔者会继续反思和优化APOS理论的四个过程，使教学过程取得更好的效果.

参考文献：

[1]Dubinsky，E.Teaching Mathematical Inductio I[J].Journal of Mathematical  Behavior，1997（16）：187-239.

[2]乔连全.APOS理论是一种建构主义[J].全球教育展望，2001 （3）：16-20.

[3]褚艳春.如何在立体几何中用好空间向量[J].学周刊，2011（11）.

[4]唐毽香.基于APOS理论的高中立体几何概念教学研究[D].湖南师范大学.2016

[5]郭芳APOS理论下立体几何线面位置关系的教学研究[D].河南大学. 2019