“双减”政策下初中数学习题课探究
闫月静





【摘要】國家提出“双减”政策,对学校教育和课堂教学提出了更高的要求。“双减”政策的实施与落实,重点在学校教育,关键在课堂教学,课堂教学应着力提升课堂效率,让每一节课都充满趣味性和探索性,提升学生的学习兴趣,让学生动手操作、动脑思考,探究知识的形成过程。
【关键词】初中数学;“双减”政策;教学实践;正方形习题课
2021年7月24日,中共中央办公厅、国务院办公厅出台了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,明确要求校内校外共同减轻学生学习负担,构建良好的教育环境。
习近平总书记在全国教育大会上强调:“教育是民族振兴、社会进步的重要基石,是功在当代、利在千秋的德政工程,对提高人民综合素质、促进人的全面发展、增强中华民族创新创造活力、实现中华民族伟大复兴具有决定性意义。”“双减”政策颁布之后,受到了社会各界的密切关注和热烈谈论,学校教育面临着更大的挑战和调整。
在“双减”政策背景下,学校课堂教学应聚焦课堂效率,优化课堂练习,提升课堂的探索性和趣味性,让学生在学习实践过程中体验到学习的快乐和成就感,在探索实践中感悟知识、获得能力。笔者以北师大版数学八年级上《正方形的性质和判定》习题课的教学设计和实践为例,探究“双减”政策下的数学习题课。
《正方形的性质和判定》是北师大版数学八年级上第一章第三节的内容,此前学生已经学习了特殊的平行四边形的性质和判定,初步具备一定的几何认知和推理能力之后,进一步对特殊的平行四边形正方形的性质和判定进行探究与证明。本节内容是在学习过正方形的性质和判定基础上的拓展和延续,也是今后学习其它平面图形的必要知识储备。正方形的性质多、判定方法多,综合性强,所以有必要在新课之后补充习题课进行强化和整合,根据北师大教材课后习题,进行编排和整合。
一、教学背景
此前,学生已经学习了特殊平行四边形的性质定理和判定定理,具备一定的探究性学习经验。正方形是特殊的菱形和矩形,具有菱形和矩形的性质,也有自己特殊的性质,研究正方形的特殊性质要从正方形的性质出发,通过预习和复习已经学习过的性质,为本节内容打好基础。
九年级的学生,其思维正向抽象转型,对事物的感性认识也逐渐丰富。本节课程让学生在学习活动中动手实践,利用正方形的性质解决问题,从已知探索未知,从已有经验探索未知,促使学生从感性认识转向理性认识,提高学生学习数学的兴趣和成就感。
二、教学目标及重难点
(一)教学目标
1.知识与技能:通过观察图形特点和动手折叠正方形等学习活动,掌握正方形的性质,能够灵活应用正方形的性质解决问题;
2.过程与方法:经历正方形折叠的探究和性质的讨论过程,丰富数学探究学习经验,培养学生动手实践能力,发展合情推理、演绎推理能力;
3.情感态度与价值观:引导学生分析问题、合理猜想,发展学生的图形处理能力,通过归纳总结,发展学生的逻辑推理能力,激发学生的探究欲,培养学生的观察能力,提升学生数学学习兴趣。
(二)教学重难点
1.教学重点:利用正方形的性质解决数学问题。
2.教学难点:通过折叠四等分正方形的面积。
三、教学过程
1.知识回顾、复习提问
师生活动:我们学习了正方形的性质和判定,请从对称性、边、角、对角线等方面思考总结平行四边形的性质,见表1。
设计意图:通过教师的引导和提问,回顾总结正方形的性质,检验学生上一节课内容掌握情况,并为本节课学习做铺垫。
2.新课引入——分割正方形
师生活动:折一折,在一个正方形的纸片上,对折两次,使得两条折痕将正方形纸片分为四个大小、形状相同的部分,请同学们与同伴讨论并动手尝试。
设计意图:此环节从折叠游戏引入,简单易操作,引导学生从观察入手,带动学生动手操作,探索折纸的方法,在与同伴讨论交流的过程中,比较方法的异同,在学生脑海中设问,埋下伏笔。
3.探索——正方形中十字形
师生活动:(1)想一想,你是怎么折叠的,你还有其它的折法吗?(2)展示分享不同的折叠方法,观察不同的折叠方法中有什么相同的特点?不同折叠方法如图1。
设计意图:通过折叠,让学生更加深刻地感悟正方形的性质,并在探索研究的过程中,发现正方形的中心十字形,感悟正方形中心的十字形特点。
师生活动:观察一下几个图形,两条折线有什么关系?总结内容见表2。
设计意图:正方形既是中心对称图形,也是轴对称图形,图形应用灵活,综合性大,通过观察可以总结出正方形中心的十字形的特点,从而归纳总结性质。
4.演绎证明——正方形中的十字形证明
师生活动:(1)探索“分割出的四个图形面积相等,并且等于正方面积的四分之一,两条折线相等”这个结论是否正确?(2)请同学认真思考,怎样证明结论的正确性。证明过程如下:
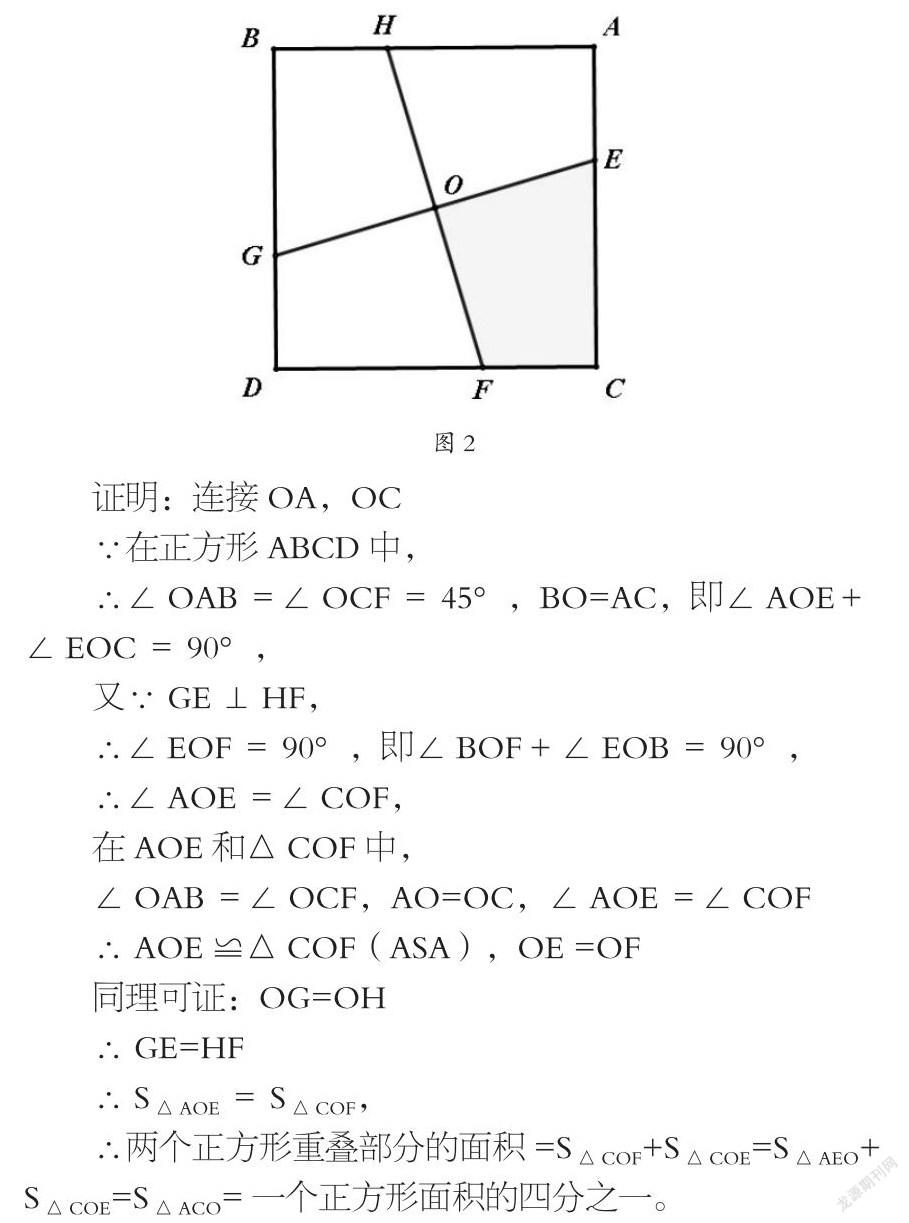
已知:如图2,正方形ABCD中,O是对角线AD与BC的交点,GE⊥HF 于O。
求证:四边形OECF的面积等于正方形面积的四分之一。
证明:连接OA,OC
∵在正方形ABCD中,
∴∠OAB=∠OCF=45°,BO=AC,即∠AOE+
∠EOC=90°,
又∵GE⊥HF,
∴∠EOF=90°,即∠BOF+∠EOB=90°,
∴∠AOE=∠COF,
在AOE和△COF中,
∠OAB=∠OCF,AO=OC,∠AOE=∠COF
∴AOE≌△COF(ASA),OE =OF
同理可证:OG=OH
∴GE=HF
∴S△AOE=S△COF,
∴两个正方形重叠部分的面积=S△COF+S△COE=S△AEO+
S△COE=S△ACO=一个正方形面积的四分之一。
由此我们得出结论:两条折线GE=HF,且分割出的四个图形面积相等,等于正方形面积的四分之一。
设计意图:通过探究得到猜想,再通过严谨的证明得出结论,并进行推广,应用到其它问题中,鼓励学生对问题独立思考,分析证明。
师生活动:通过折纸和探究活动,能够得出什么结论?
设计意图:引导学生深入思考,总结归纳,教师不急于给出结论,应让学生充分思考和总结,再由学生回答,让学生成主体,以学生为中心。在正方形中,过正方形中心的两条相互垂直的直线,将正方形的面积四等分,并且这两条直线与正方形的边相交,所得的两条线段相等。
5.巩固练习,能力提升
师生活动:如图3,正方形ABCD的对角线AC和BD相交于点O,正方形ABCD与正方形A'B'C'O的边长相等。在正方形A'B'C'O绕点O旋转的过程中,猜想两个正方形重叠部分OMCN的面积与正方形ABCD的面积有什么关系?请对你的猜想进行分析和证明。
解:∵四边形ABCD是正方形,四边形OA'B'C'是正方形,
设两个正方形的交点为M和N
∴AC=BD,OB=OC,∠OBM=∠OCN=45°,∠A'OC'=90°,
∵∠BOC=∠A'OC'=90°,
∴∠BOM=∠CON,
∴△BOM≌△CON(ASA),
∴BM=CN.
(2)∵△BOM≌△CON,
∴S△BOM=S△CON,
∴S四边形OMBN=S△OBC= S正方形ABCD.
设计意图:通过图形的变换,探究结论,让学生经历性质探究、结论证明、应用结论几个环节,形成知识,掌握能力。此题应给学生留白思考的时间,让学生完整地证明此题,书写过程,并强调几何书写的规范性。
在随堂练习的环节中,进行针对性的训练,以巩固本节课的学习内容。练习的难度应由浅入深,循序渐进,题目可以引入有趣且贴近实际的情境问题,以引发学生共鸣。此外,随堂练习可以分层训练,内容多少也可由学生程度适当选择。
6.提炼概括,回顾小结
师生活动:回顾小结:如图4,过正方形中心的十字形的特点:如果过正方形中心的两条线段互相垂直,那么它们相等并且均分正方形,分割的图形是全等形。
四、教学反思
教师依据教学设计来实施教学,关键在于学生的可能表现状态,以学生为主体,但也不能完全按照学生的状态进行,要紧紧围绕着教学目标进行,并且充分关注学生数学思维的形成,根据思维情况进行调整。在课后作业的设计上,要以分层作业为主,充分给学生个性化的发展,确切落实“双减”政策。
“双减”政策的实施与落实,重点在学校教育,关键在课堂教学。教师要研究课程标准,研究教法、教材、习题,在不增加难度、不增加課时、超赶进度的前提下,巧妙利用习题课,增加课堂的趣味性,提高内容的探索性,让课堂充实,让效率提高,让智慧叠加,让学生学有所得。
参考文献:
[1]中共中央办公厅,国务院办公厅.关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见[OL].http://www.moe.gov.cn/jyb_xxgk/moe_1777/moe_1778/202107/t20210724_546576.html.
[2]顾明远.新时代教育发展的指导思想——学习习近平总书记在全国教育大会上的讲话[J].北京师范大学学报(社会科学版),2019(1):5-9.
[3]刘蓉.初中数学课堂教学中引导学生开展探究性学习的研究[D].山东师范大学,2006.
责任编辑 陈 洋

