“变”中求“不变”，立意高又远

曾昌涛

[摘  要] 数学核心素养的关键在于提高學生的思维品质，思维的动态迁移，在“变”与“不变”中辩证统一与有效生成. 在几何图形变化过程中抓住不变的几何性质，可使解题化难为易.

[关键词] 核心素养;试题探析;立意;平移变化

试题回眸

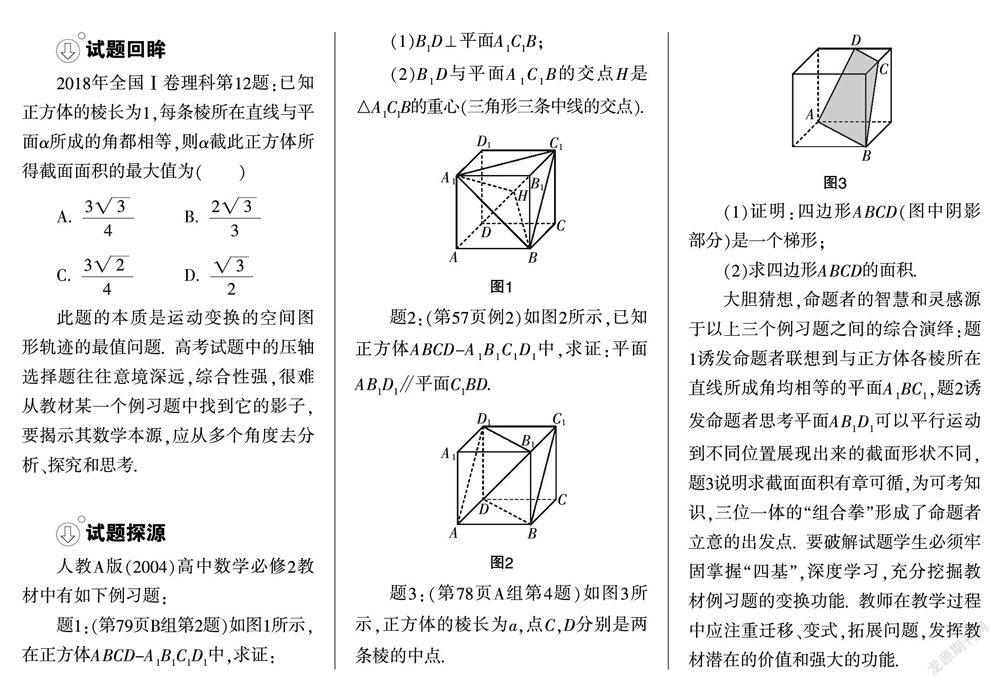
2018年全国Ⅰ卷理科第12题：已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（  ）

此题的本质是运动变换的空间图形轨迹的最值问题.高考试题中的压轴选择题往往意境深远，综合性强，很难从教材某一个例习题中找到它的影子，要揭示其数学本源，应从多个角度去分析、探究和思考.

试题探源

人教A版（2004）高中数学必修2教材中有如下例习题：

题3：（第78页A组第4题）如图3所示，正方体的棱长为a，点C，D分别是两条棱的中点.

（1）证明：四边形ABCD（图中阴影部分）是一个梯形;

（2）求四边形ABCD的面积.

2005年全国联赛试题：在正方体ABCD-A′B′C′D′中，任作平面α与对角线AC′垂直，使得α与正方体的每个面都有公共点，记这样得到的截面多边形的面积为S，周长为l，则（  ）

A. S为定值，l不为定值

B. S不为定值，l为定值？摇

C. S与l均为定值

D. S与l均不为定值？摇

问题探究

1. 图形演化

那么在所有正三角形以及六边形的截面图形中，哪一个面积最大呢？

2. 解法剖析

数学学科六大核心素养本质上反映的是数学思维品质，思维的动态迁移而非刻舟求剑[1]. 在“变”与“不变”中辩证统一，动中求静，突破思维局限，“莫让浮云遮住眼，除尽繁华识真颜”，解决考题的关键是要从图形运动变化过程中抓住不变的几何性质.

解法1：截面面积（变）？圳大圆中内接正六边形面积最大（不变）.

为什么满足条件的图形中正六边形EFHMNQ的面积最大呢？下面设计一个数学实验来解释它：

不妨设在正方体内放一个内切球，易知正方体的中心与球心O重合. 满足条件的平面α与球O所截的图形是圆，当平面α经过球心O时所得的截面是大圆（在所有圆中面积最大），借助于数学常识“圆内接n边形中，面积最大的为正n边形”可知，当平面α平移经过球心O且六边形恰为正六边形（中心为O）时面积最大.

结束语

波利亚认为：“数学问题的解决仅是一半，更重要的是解题后的回顾.”[2]提出一个问题比解决一个问题更难，问题解决后要去归纳、反思，挖掘其背后的立意出发点，品味其高妙之处.

（1）从知识层面分析：立体几何的图形载体为柱、锥、台、球，主干知识是平、垂、角、积. “平”“垂”为空间特殊位置关系，指线与线、线与面、面与面的平行和垂直关系;“角”指空间的三种角：异面直线所成角，直线与平面所成的角，二面角的平面角;“积”指几何体的面积（侧面积、表面积）和体积. 试题正是以正方体为几何载体，考查的是正方体中线面、面面平行和垂直关系，直线与平面所成的角，截面面积等重点内容，可谓一线串几珠，金玉蕴其中.

破题者将面临三道难关：一是与各棱所在直线所成的角均相等的平面α是怎样的平面？二是平面α在平移过程中的截面图形分别是何种形状？三是所有截面中为何正六边形的面积最大？特别是第三道难关，在考试过程中学生仅凭观察、猜想，代替不了严密的逻辑证明.

（2）从思想方法层面分析：试题考查了函数与方程、化归与转化、运动与变换、数形结合等重要的数学思想方法，发展和提高学生的空间想象能力、推理论证能力、运算能力等是学习立体几何的根本任务，在“变”中求“不变”，试题为教学中灵活运用立体几何知识分析问题和解决问题提供了素材.

（3）从数学核心素养层面分析：试题考查了直观想象、数学建模、逻辑推理、数学运算等核心素养. 试题立意高远，可作为典型例题去拓展、迁移、变式以达到触类旁通的教学效果，破题中没有厚重的知识沉淀和方法积累，思维深度达不到解题的终点.

参考文献：

[1]  李建国. 例析核心素养导向的高考试题——以2018年高考全国卷Ⅰ理科第12题为例[J]. 中学数学研究（华南师范大学版），2019（10）：44-45+19.

[2]  潘静. 直观固然好 论证不可少——对一道高考题的解答探究及教学思考[J]. 中学数学教学参考，2020（34）：59-60.