关于《有限长带电导体直线的电荷分布》的商榷
周群益,周丽丽,莫云飞,侯兆阳
(1. 广州理工学院 通识教育学院,广东 广州 510540;2. 赣南医学院 医学信息工程学院,江西 赣州 341000;3. 长沙学院电子信息与电气工程学院,湖南 长沙 410022;4. 长安大学 理学院应用物理系,陕西 西安 710064)
文献[1]研究了有限长带电导体直线的电荷分布规律.作者首先利用带电导体椭球面的面电荷分布公式,将其转化为旋转椭球面的面电荷公式,再在直线上用投影的方法证明了电荷线密度公式:
(1)
其中,Q是所带电量(默认Q>0),a是带电线段的半长,x是导体上的点到中心的距离.第2种方法就是利用带电椭圆面的电荷在直线上投影推导第2个电荷线密度公式:
(2)
第3种方法就是用圆环带电导线在直线上的投影推导出第3个电荷线密度公式:
(3)
3个公式都在分母中出现根函数,可称之为根式分布规律.但是各式系数不同,说明推导过程有瑕疵.有文献[2]证明:圆形导体薄板的电荷遵守根函数分布规律.我们也证明:无限长导体薄板的电荷也遵守根函数分布规律[3].我们曾经猜想:导线线段还是遵守根函数分布规律的.后来证明,这种猜想是错误的.通过等势线和电场线图形说明式(1)是错误的,因而式(2)和(3)也是错误的.
本文用多种方法推导了同一个线密度公式,证明了带电导体线段的电荷是均匀分布的.有文献[4]推导了均匀带电线段的等势线是椭圆,电场线是双曲线,但是过程不详细,也没有说明均匀带电线段是导体.本文详细地推导了等势线的方程和电场线的方程,通过等势线方程的极限情况,证明了均匀带电线段是等势线.通过电场线与线段垂直,证明了均匀带电线段就是导体.文本最后说明了电荷之外拉普拉斯方程成立,进而证明了均匀带电线段是导体.
1 用导体椭球面电荷分布公式求导体线段的电荷分布
带电导体椭球面电荷分布的面密度公式为[5-6]
(4)
其中,上标E表示椭球面,a、b和c分别是椭球面的3个半轴.椭球面方程为
(5)
设b=c=R,则椭球面变成旋转椭球面,电荷面密度为
(6)
上标R表示旋转椭球面.将旋转椭球面的方程变
形为
将其代入式(6)可得
(7)
文献[1]根据电荷等量关系认为λdx=σ2πRdx,σ=σ(R),当R→0时求得式(1).这种关系将y误作R,就是将旋转椭球面变成了旋转圆柱面,因而推导出错误的结果.严格说来,dx应该改为孤元ds,只是当R→0时,ds→dx.
旋转椭球面在Oxy平面的截面如图1所示,R是椭圆纵半轴,椭圆的参变量方程是
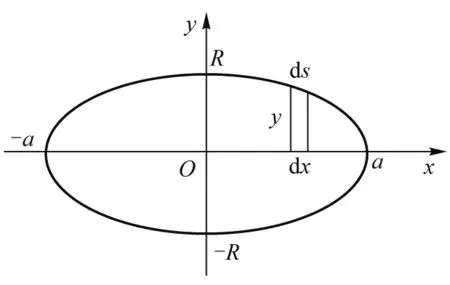
图1 旋转椭球面在Oxy平面的截面
x=acosθ,y=Rsinθ
(8)
微分为
dx=-asinθdθ,dy=Rcosθdθ
(9)
弧元是
(10)
弧元ds绕x轴旋转一周的面积元是
(11)
其所带的电荷量为
dq=σ(R)dS=
(12)
当R→0时,旋转椭球面退化为一条长为2a的线段,电荷投影在线段上,其线密度为
(13)
可见带电导体线段的电荷分布是均匀的.
2 用导体平面电荷分布公式求导体线段的电荷分布
2.1 利用椭圆的面电荷公式
在式(4)中,当c→0时,三维椭球面就退化为二维椭圆面,由于一个椭圆面是一个椭球面上下两部分重叠的结果,所以电荷的面密度为
(14)
上标P表示平面.将椭球面方程变形为
将上式代入式(14)可得
(15)
文献[1] 根据电荷等量关系认为λdx= 2σbdx,σ=σ(P)/2,从而求得式(2).这种关系将y误作b,就是将椭圆变成了矩形,因而推导出错误的结果.
椭圆面如图2所示,上半椭圆的方程为
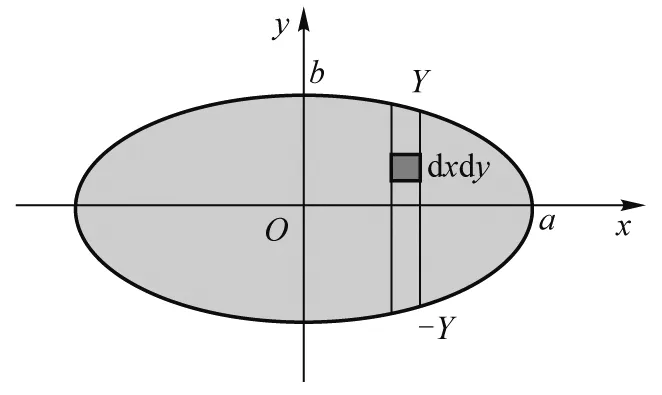
图2 椭圆面上的面积元
(16)
由式(15)可得电荷的面密度为
(17)
在椭圆面中取一个面积元dxdy,其所带的电荷量为
d2q=σ(P)dxdy
宽为dx的条形面积元所带的电荷量为
(18)
这些电荷投影在x轴上,电荷的线密度为
(19)
结果与式(13)的结果完全相同.
2.2 利用圆的面电荷公式
在式(15)中,令b=a,椭圆就变成了圆,利用圆的方程x2+y2=ρ2,可得导体圆面电荷分布公式:
(20)
上标C表示圆面.这是圆形导体薄板电荷面密度的根式分布规律,与均匀球面电荷在平面上投影的面密度公式是完全相同的[2].
利用式(20)也能证明式(19).上半圆的方程为
(21)
式(20)可化为
(22)
在圆面中取一个面积元dxdy,其所带的电荷量为
d2q=σ(C)dxdy
宽为dx的条形面积元所带的电荷量为
这个积分的形式和结果与式(18)相同,因而电荷的线密度就是式(19).
3 用导体球面电荷分布公式求导体线段的电荷分布
由于均匀带电圆环不是封闭的等势面,所以不能用文献[1]的第3种方法通过投影法求得导体线段的电荷分布公式.
设导体球面半径为a,带电荷量为Q,均匀分布在球面上,电荷的面密度为
(23)
上标S表示球面.在式(2)中,令b=c=a,并利用球面方程x2+y2+z2=a2也可以得到上式.
球面在Oxy平面的截面如图3所示,圆的参变量方程为
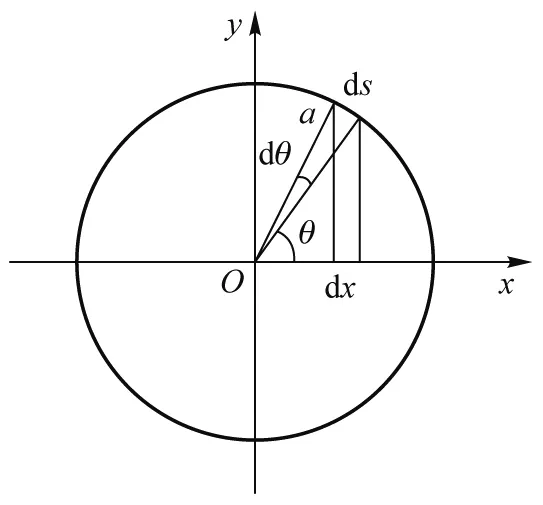
图3 球面在Oxy平面的截面
x=acosθ,y=asinθ
(24)
弧元ds=adθ绕x轴旋转一周的面积元是
dS=2πyds=2πyadθ
其所带电荷量为
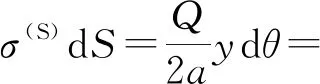
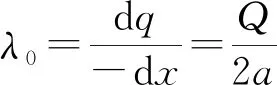
结果完全相同而方法更简单.再次证明:带电导体线段的电荷分布是均匀的.
其实,作者最初就是用这种方法证明了均匀带电线段是导体,因而对文献[1]的结果提出了质疑,进而发现了错误,从而得出正确的结论.当然,这个结论还需要通过多方面验证.
4 电荷线密度根式分布的电势和场强以及可视化
4.1 电势和场强的表达式
用(x,y)表示二维空间场点的坐标,电荷线密度根式分布式(1)可表示为
(25)
如图4所示,建立坐标系,在线段上取一线元dl,其所带电荷量为dq=λdl,线元到场点P的距

图4 带电线段的电势
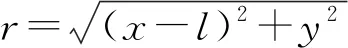
(26)
产生电势为
其中k为静电力常数.取无穷远处为电势零点,线电荷产生的电势为
注意:上式是收敛的瑕积分.设l=asinθ,则dl=acosθdθ,上式化为
(27)
当y=0时,可得
(28)
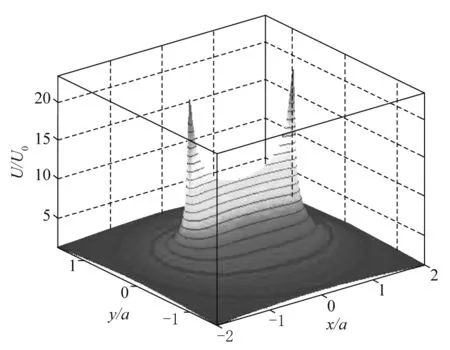
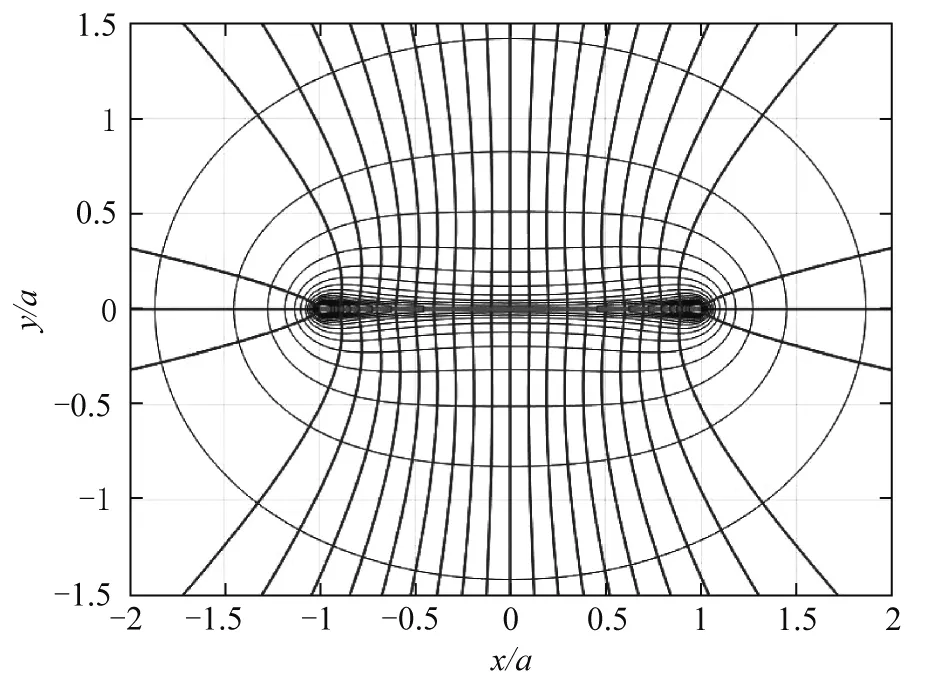
在|x| E(x,y)=-U(x,y) (29) (30) 场强也可以求数值解. 取U0=kλ0为电势单位,则根式分布电荷的无量纲电势为 其中x*=x/a,y*=y/a是无量纲的坐标. 设E0=U0/a=kλ0/a,取E0为电场强度单位,则无量纲的电场强度为 E*(x*,y*)=-*U(x*,y*) 根据数值电势可以求数值电场强度. 将公式无量纲化之后即可用MATLAB梯形求和函数trapz求电势的数值积分之值,用梯度函数gradient求电场的两个分量,用等高线指令contour画等势线,用流线指令streamline画电场线[7]. 1) 当电荷线密度按式(1)分布时,其电势U(x,y)的曲面和三维等势线如图5所示,电势在线段端点有两个尖锐的“峰”,这是因为两个端点的电势为无穷大.当电势比较低时,三维等势线是同时包围两个“峰”的对称的封闭曲线;当电势比较高时,三维等势线是分别包围两个“峰”的两条封闭曲线.两“峰”之间电势的变化十分显著.三维等势线在Oxy平面上的投影就是二维等势线. 图5 根式分布线电荷的电势面和三维等势线 2) 当电荷线密度按式(1)分布时,二维等势线和电场线如图6所示,当电势比较低时,等势线是包围线段的凸形曲线;当电势比较高时,等势线是靠近带电线段的凹形曲线;当电势很高时,等势线变成分别绕端点的曲线,这种曲线穿过了线段.后面两种情况是因为线段两端的电荷线密度比较大所造成的.电场线与等势线正交,但是明显不垂直于带电线段,说明线段不是导体,因此式(1)不可能是带电导体线段的线密度公式.由于式(2)和式(3)与式(1)只有系数不同,所以也是错误的. 图6 根式分布线电荷的等势线和电场线 电磁学教材通常都会推导均匀带电线段的电势和电场强度的公式,有的教材还画出了电场线和等势线[7].如图4所示,当电荷线密度是均匀分布时,电荷元产生电势为 线电荷产生的电势为 (31) 无穷远处是电势零点.当|x| 当电势为常数时,设c=exp(U/kλ0),c>1,则 两边平方后,化简可得 移项可得 再平方后,化简可得 (32) 这是椭圆方程,两个半轴分别为 (33) (34) 其中,c是由电势决定的无量纲参数.当U→+∞时,可得c→+∞,因此A→a,B→0,这时,等势线的椭圆退化为一条长为2a的线段,可见:均匀带电线段就是一条等势线. 电场强度的两个分量分别为: (35) (36) (37) 将式(35)和式(36)代入上式,用凑微分法可得微分方程为 积分可得电场线的代数方程为 再平方后化简可得 (38) 这是双曲线族.实半轴和虚半轴分别为 (39) (40) 其中,c是由电场线的起点决定的参数.令c=0,则得x=0,双曲线退化为一条竖直线,这就是y轴;令c=±a,则得y=0,双曲线退化为x轴上除了带电线段之外的左右两条水平射线. 取a为坐标单位,可以将椭圆的参变量方程无量纲化.在MATLAB中取无量纲的电势为向量,计算无量纲的常数c向量,将参变量θ也取为向量,用meshgrid函数化为矩阵,即可计算两个坐标,用plot指令画出椭圆曲线族.同理,取a为坐标单位,可以将双曲线的参变量方程无量纲化,c/a是无量纲的常数,用同样的方法绘制双曲线族. 均匀带电线段的等势线和电场线如图7所示,等势线是包围线段的闭合的对称曲线族,等势线的电势U从外到内依次取为(1,2,…,7)kλ0,电势越高,椭圆就越扁平,当电势U趋于无穷大时,等势线趋于线段.电场线是双曲线族,与椭圆等势线族处处正交,也垂直于带电线段,说明场强在线段表面只有垂直分量,带电线段就是导体. 图7 均匀带电线段的等势线和电场线 带电导体之外的电势应该满足拉普拉斯方程: (41) 手工计算电势对坐标的二阶偏导数十分麻烦,借助于MATLAB的符号计算,可大大提高计算效率. (42) 式(31)可化为 U(x,y)=kλ0[u1(x,y)-u2(x,y)] (43) 其中 (44) u1(x,y)对坐标的两个二阶偏导数分别为 (45) (46) 同理可得 (47) 由于均匀带电线段是在三维空间激发电场的,电势应该表示为 (48) (49) 式(48)可化为 U(x,y,z)=kλ0[u1(x,y,z)-u2(x,y,z)] (50) 其中 (51) u1(x,y,z)对x和y的二阶偏导数在形式上就是式(45),u1(x,y,z)对z的二阶偏导数为 (52) 本文指出了文献[1]中的错误和发生错误的原因,用多种电荷投影法证明:导体线段所带的电荷是均匀的.本文求出了均匀带电线段的等势线方程和电场线方程,证明均匀带电线段是等势线,电场线与线段垂直,利用等势线和电场说明均匀带电线段是导体. 画图是检验公式正确与否的最直观的方法.通过电势曲面和等势线与电场线说明根式分布的电荷不可能是导体,也通过画图显示均匀带电线段是导体.掌握MATLAB的符号计算方法可以大大提高计算和研究效率.在这类问题中最好将电势公式分解为最简形式,然后计算二阶偏导数的和,最后化简.这种方法可以检验电势是否满足拉普拉斯方程,从而判断带电体是否导体.
4.2 电势和场强的无量纲化和可视化

5 电荷线密度均匀分布的电势和场强以及可视化
5.1 等势线方程
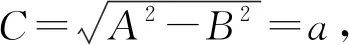
5.2 电场线方程
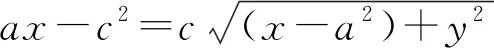
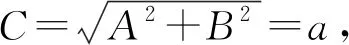
5.3 电场的可视化
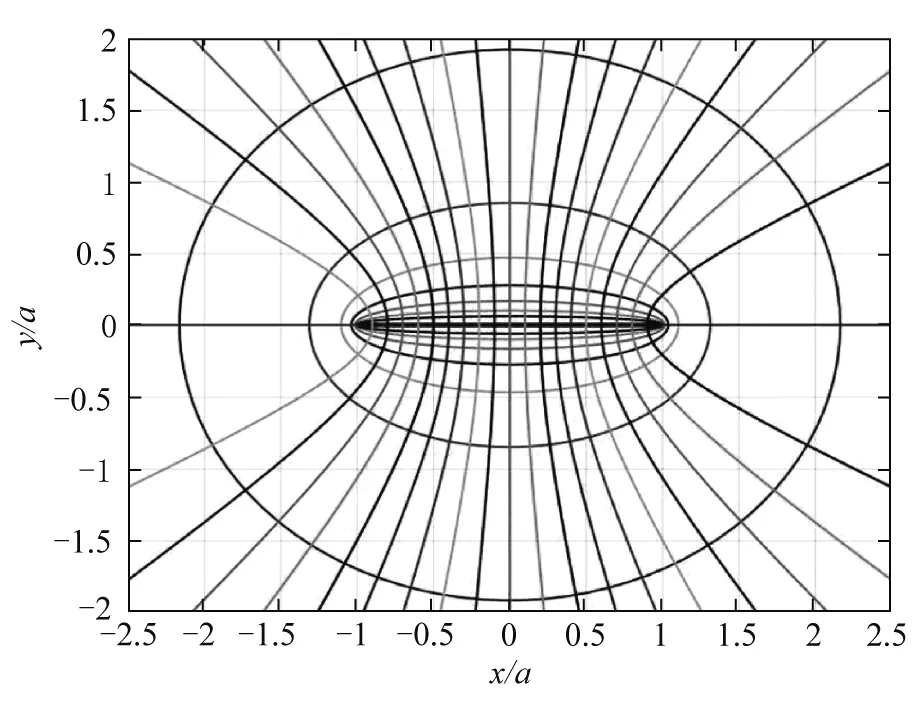
6 均匀带电线段电势的拉普拉斯方程证明

6.1 二维拉普拉斯方程问题
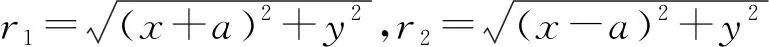
6.2 三维拉普拉斯方程问题
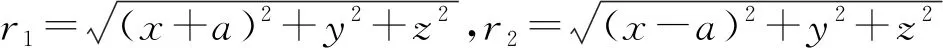
7 结束语

