均质Reuleaux多边形平板转动惯量的求解

张会均，陈 靖，蒋逢春，王世卓

( 郑州轻工业大学 物理与电子工程学院，河南 郑州 450001 )

Reuleaux三角形是德国机械工程Franz Reuleaux提出来的. Reuleaux三角形是以正三角形的三个顶点为圆心，以其边长为半径作圆，在三个圆的交汇处，由三段圆弧组成的一种特殊图形. 当它在地面滚动时，其高度始终不变，为正三角形的边长，因此也称此类曲线为等宽曲线. 高度相同的等宽曲线具有相同的周长，其中圆的面积最大，Reuleaux三角形的面积最小. 等宽曲线的应用比较广泛，例如，Reuleaux三角形钻头可钻出正方形的孔洞，Reuleaux五边形钻头则能给出正六边形的钻孔，这能满足一些特殊的工业设计需求；马自达Renesis转子发动机的转子截面是Reuleaux三角形[1]，相对于传统活塞式发动机，转子发动机体积小，质量轻，运行平稳，噪声小，相同排量的转子发动机的输出功率和扭矩更大.

转动惯量用来衡量刚体发生转动时惯性的大小，刚体转动惯量的计算是大学物理教学的一类典型题目. 本文以匀质的Reuleaux多边形刚性平板为研究对象，求解绕过质心并垂直于平板转轴的转动惯量.

1 Reuleaux三角形板

1.1 方法1：扇形+弓形

图1 Reuleaux三角形

转轴命名的规则如下，第1个字母代表转轴通过的点，第2个字母P代表垂直于平板的轴，例如OP指过质心O并垂直于平板的转轴. 求解Reuleaux三角形板绕质心轴OP的转动惯量IReu-3，可先求绕AP轴的转动惯量IA. 如图1(a)所示，将Reuleaux三角板分成3个区域，则有IA=IAI+IAII+IAIII=IAII+2IAI. 扇形区域II的转动惯量IAII以A为圆心，半径L3圆盘的1/6，有

(1)

设平板的面质量密度为σm,求解弓形区域I的转动惯量，可建立如图1(b)所示的极坐标系，圆心角为dθ的阴影区域是以A为圆心，半径为2L3cosθ圆盘的一部分,其转动惯量为

(2)

则

(3)

因此

(4)

根据平行轴定理，Reuleaux三角形板绕OP轴的转动惯量：

(5)

其中

(6)

是Reuleaux三角形的面积. 半径为R的圆盘绕OP轴的转动惯量：

(7)

由式(5)可得

(8)

即Reuleaux三角形板的转动惯量约为外接圆盘的47.1%.

1.2 方法2：正三角形+弓形

将Reuleaux三角形分为一个正三角形和三个弓形. 匀质正三角形平板绕OP轴的转动惯量[3]为

(9)

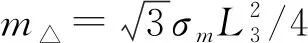
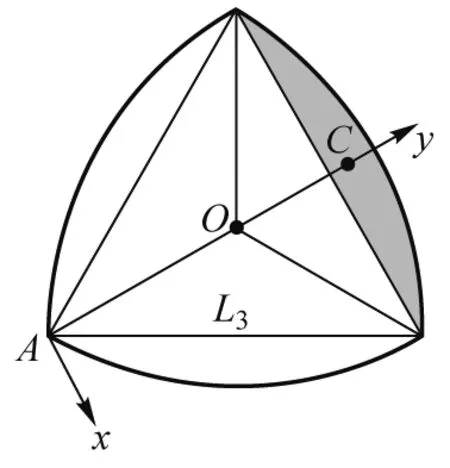
图2 弓形质心C

IOC=IC+mCOC2,

IAC=IC+mCAC2,

IA△=IO△+m△R2,

(10)

上式中IOC、IAC和IC分别是弓形绕OP、AP和其质心轴CP的转动惯量，IA△是正三角形绕AP轴的转动惯量，IAL3是以A为圆心，半径为L3的圆盘绕AP轴的转动惯量,mC是弓形的质量.

弓形质心的y坐标为

(11)

联立式(9)—(11)，并考虑

IReu-3=IO△+3IOC

(12)

可得到与式(8)相同的结果.

上述2种方法的区别主要在于对Reuleaux三角形板的分区方式. 方法1是分区积分的，由于A点不仅在扇形II的圆心处，也在弓形I、III的圆弧上，因此可以用积分的方法求解IA；方法2则是将其分为正三角形和弓形，需要确定出弓形的质心位置，并根据平行轴定理求解IOC，优点是此过程用到了IC但不涉及具体求解.

2 Reuleaux多边形板

Reuleaux多边形板转动惯量采用方法1直接积分求解有一定的困难，以图3(a)中Reuleaux五边形为例，由于A点与区域I和III有直接关系，可直接积分求解绕AP轴的转动惯量，而对于区域II来讲，A点既不是圆弧的圆心，也不在圆弧的圆周上，直接积分求解区域II绕AP轴的转动惯量有一定的困难.

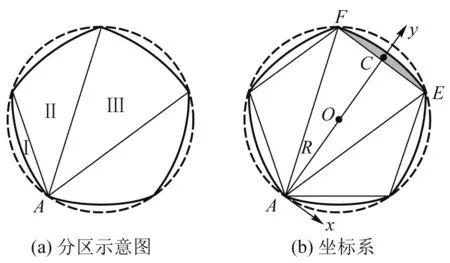
图3 Reuleaux五边形

边数为N的ReuleauxN边形可看作由内接正N边形和N个弓形组成，则ReuleauxN边形绕OP的转动惯量：

IReu-N=ION+NIOC

(13)

ION和IOC分别是正N边形[3]和弓形绕OP轴的转动惯量

(14)

其中

分别是正N边形的质量、边长和内切圆半径. 设点C是ReuleauxN边形其中一弓形[图3(b)阴影区]的质心，根据平行轴定理,有

(18)

上式中IOC、IAC和IC分别是弓形绕OP、AP和CP轴的转动惯量.IALN是以A为圆心，半径为LN的圆绕AP轴的转动惯量.IA△是三角形AEF[如图3(b)所示]绕AP轴的转动惯量.IA-2N是以A点为中心，正2N边形绕AP轴的转动惯量，其中心点A到其顶点E、F的距离是LN，LN同时也是ReuleauxN边形圆弧的半径.IA-2N的计算需要用到式(14),但要注意相关参数需要对应变化.

弓形的质心坐标：

(19)

其中弓形的质量为

(20)

联立式(13)—(20)可得到IReu-N，具体将在第3节与数值积分结果对比讨论.

3 数值积分

匀质刚体绕转轴OP的转动惯量定义如下

(21)

其中r是质元dm到转轴的距离. ReuleauxN边形绕OP轴转动时具有N重旋转对称性，所以只需要求其1/N(如图4中的阴影区域)的转动惯量即可.

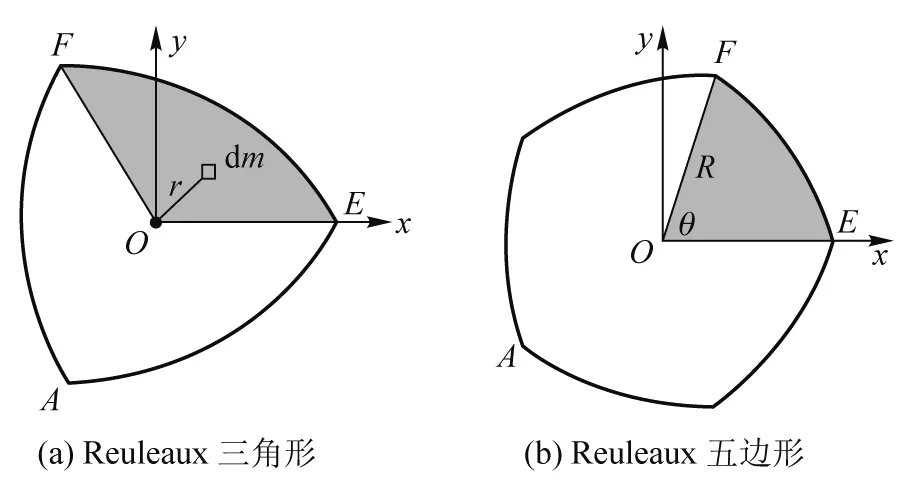
图4 坐标系

图4(a)中Reuleaux三角形的阴影区域分布在一、二象限，当边数N>3时，多边形的1/N[以图4(b)阴影区为例]仅分布在第1象限. 图4中OE=OF=R是外接圆半径. 图4(a)中阴影区坐标(x,y)的约束条件是

(22)

图4(b)中ReuleauxN边形阴影区的圆心角θ=2π/N，阴影区坐标(x,y)的约束条件是

0≤x≤R, 0≤y≤xtanθ

(23)

(24)

则基于式(21)，Reuleaux N边形的转动惯量可写为

(25)

实现式(25)所使用的编程语言是Fortran95，计算相关的物理量均设置为双精度. 取面元ds=dxdy为正方形，dx=dy是两个方向的积分步长，并取R=1(SI)，σm=1(SI). 数值求解IReu-N的精度取决于面元ds的大小，所以需要先进行面元ds的大小的收敛测试，令

(26)

为ReuleauxN边形板转动惯量与其外界圆盘的比值，显然当N→∞时有ηN→1，式(8)给出了解析结果η3=0.470 556 583 4(保留10位有效数字).

表1列出了面元ds的大小对η3的影响及相对误差，随着ds的减小，η3的结果趋向解析结果，相对误差也随之降低. 数值积分的误差一方面是因为当考虑面元到转轴的距离时，忽略了面元本身的大小，另一方面是当面元恰好在阴影区边界处时，面元的一部分是在阴影区之外的，注意，这两种误差来源均可通过减小面元来降低. 但考虑数值结果的精度和计算效率，在后续的计算中均取ds=4.00E-10(SI).

表1 η3数值解的收敛测试

计算ηN时,IReu-N分别使用解析式(13)和数值积分式(25)就得到了表2中ηN的解析与数值结果，表2中的下划线是数值解与解析解不同的部分，数值解的相对误差随着N的增大而增大，这是因为相同的ds所带来的误差在1/N的ReuleauxN边形中的占比更大，表2中的结果也表明了Reuleaux多边形板的转动惯量随着N的增大也愈趋近于其外接圆盘.

表2 ηN的解析解与数值积分结果

需要注意的是，ReuleauxN边形的边数N只能取奇数[4]. 图5中列出了ReuleauxN边形板与正N边形板的转动惯量相对于外界圆盘的比例. 当N较小时，两者相差较大，例如IReu-3是其外接圆盘的47.06%，而I△仅为其外接圆盘的20.67%；随着边数N的增大，ηN→1,此时正多边形板、Reuleaux多边形板的结果都向其外接圆盘趋近，例如，IReu-27可达外接圆盘的99.1%，正27边形板的转动惯量是其外接圆盘的98.2%.

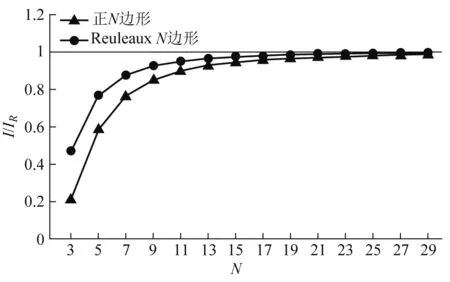
图5 转动惯量相对于外接圆盘的比例

4 结语

匀质Reuleaux多边形平板转动惯量的解析解与数值解的相互吻合，印证了求解方法的正确性，并定量地给出了一些符合理论变化趋势的结论. Reuleaux多边形是一类特殊的等宽曲线，每个圆弧边所对的圆心角相同，内嵌的是正多边形，其实只要对角线相等而边长不一定相等的奇数多边形都可形成等宽曲线. 等宽曲线型平板转动时的高度虽然不变，但其质心高度却是时刻变化的，因此并没有广泛应用在车轮上. Reuleaux多边形等宽曲线在互关联干涉成像仪的设计上也有相关应用[5].

根据等宽曲线的特征，Reuleaux多边形平板容易推广到沿各个方向滚动高度都不变的Reuleaux多面体，但与Reuleaux多边形平板不同的是，Reuleaux多边体的类型是有限个数的，其转动惯量可通过内接正多面体[6]和若干球冠的结果叠加得到.