基于自适应优化控制的车体垂向加载系统
郭璇,赫东海,张向海,许平,王倩,李成福
(1.中车长春轨道客车股份有限公司 国家轨道客车工程研究中心,吉林 长春130113;2.吉林省经济管理干部学院 机电工程学院,吉林 长春130012;3.中南大学 交通运输工程学院,湖南 长沙410075)
随着城镇化发展与城际互联互通日益加深,轨道交通的需求量日益增大,人们对轨道车辆的性能要求也越来越高,轨道车辆的安全性问题逐渐受到人们的重视。轨道车辆车体的安全性是确保轨道车辆整车安全性的基础[1]。车辆设计时的车体型式试验是确保车体安全性的重要手段。车体型式试验的目的是校核轨道车辆车体力学性能是否能满足车辆实际运营要求,主要包括静强度试验和动应力试验等[2-3]。其中,静强度试验是基础。国内外轨道车辆相关标准均对车体静强度试验做出规范[4-6]。根据标准要求,车体静强度试验的工况通常包括:垂向载荷工况、纵向拉压载荷与垂向载荷合成工况、扭转载荷与垂向载荷合成工况等。由此可见,垂向载荷是车体静强度试验各工况的基础载荷。目前,静强度试验的垂向载荷施加方式常采用传统的人工搬运重物(砝码或沙袋)至车体地板上进行加载的方式。虽然某些单位或研究机构设计了相关垂向加载装置,由于没有设计出合适的配套控制系统,实际加载效果与期望效果相差较大。因此,当加载精度要求较高时,还需回归原始的人工加载方式。出现这一现象的原因在于以下几点:1)静强度试验要求的垂向载荷通常较大,且载荷施加要求均布,使用单点设备达到载荷均布是非常困难的。相比较,分布式多点施加载荷能较易实现载荷均布,也较易实现各加载位置载荷的调节,因此,目前考虑使用分布式多点加载装置。2)若应用分布式多点加载装置,如何协调各加载点的加载力大小是准确实现载荷均布的关键。但各加载点耦合关系复杂,每个加载点对于车体整体垂向载荷的贡献较难准确给出。目前,大多依据经验估算或现场实车调节各点加载力大小,使加载力均布。这种做法直接影响了垂向加载的精度。3)由于每个车体结构不同,门窗分布不同,因此,致使加载设备的加载点分布必不相同。仅凭经验难以快速实现车体垂向载荷均布,只能使用不断尝试调节加载装置各点加载力的方法,这大大降低了试验效率。针对以上问题,本文通过软硬件整体设计,提出一种基于自适应优化控制的车体垂向加载系统,能够较好地解决以上提到的多点加载系统解耦难、加载系统适应性差的问题。该系统基于遗传算法能够实现各个加载点的最优寻解,求解各个加载点最合适的加载值;PID控制器为系统加载力的自适应调节提供了条件,通过反馈机制和遗传算法二次寻优,可最大限度地使实际加载力靠近目标加载值,从而实现自适应优化控制。当该系统能够将车体垂向载荷施加到任意自定义值时,实现车体垂向均布加载将不是问题。因此,本文以均布载荷自适应调节到自定义载荷为案例,证明本垂向加载系统设计的可行性。
1 垂向加载系统组成
本文以较为常见的A型城铁车辆为对象进行垂向加载系统设计。整个加载系统主要包括软硬件2部分,其中,硬件部分包括加载装置和液压系统。
1.1 多点加载装置设计
加载装置是整个垂向加载系统的躯干,它是载荷的直接作用单元。本加载装置设计充分考虑了目标对象结构的特殊性、施加载荷分布要求和现场可用资源情况,力求结构简单,装配及可用性最优。
如图1(a)所示为A型地铁车Mp车车体及其加载装置示意图。根据实际工况,垂向载荷需施加的载荷仅为施加在车体内地板上的重力。重力为外力,应注意的是,所施加的力不应是形成车体内部的内力,所施加的载荷应是通过力传递从外部结构传递到车体内部的外力。因此,简单地采用车体内部车顶和地板作用力和反作用力支撑加载的方式不符合载荷施加要求。
从车体结构来看,车体为封顶结构。因此,加载装置只能通过车体侧面的门窗口伸入到车体内部,通过力传递完成载荷施加。加载设备伸入的路径有对称的5个侧门口,2个端门口和对称的4个窗口。此处选用尺寸较大的门口将设备伸入,如图1(a)所示。
如图1(b)为加载装置侧视图。加载装置的力传递可概括为[7]:用螺栓将地坪的滑槽结构与加载梁紧固,使加载梁有足够向下的夹紧力;然后,向下的夹紧力通过加载梁传递到车体内液压缸上端,形成对液压缸向下的压力;当液压缸进油伸长,加载梁向下的压力迫使液压缸下部对枕木产生向下的垂向载荷,枕木的垂向载荷作用在车体地板上完成地板的垂向加载。为模拟实际工况,车体的反向支撑点均在空簧位置,也可直接选用转向架支撑。

图1 加载系统示意图Fig.1 Schematic diagram of the loading system
总结看来,本套加载装置由5个加载梁,10个加载液压缸,5套枕木,2个假台组成,共10个均布加载点,4个集中支撑点。
1.2 液压回路设计
基于上述车体加载装置,设计对应的液压回路。为精确控制加载力大小,便于单独调节和各加载点载荷解耦,各个加载点均需配置独立的液压控制模块。每个加载点加载工况相同,因此,应设计成等效的加载结构,各加载点的液压模块完全相同。
液压模块原理简图如图2所示。为便于精确控制,本液压回路采用伺服比例换向阀控制液压缸加载或卸载,调节进油量,进而调节液压缸作用力[8]。液压回路配有电驱动变量泵,变量泵也可实现液压缸载荷调节。加载时,载荷需稳定一段时间。因此,需要设计机制使液压缸保持一定压力,这里采用安全阀和比例溢流阀组成双向控制流量且反向锁紧回路,同时,起到过载保护作用。单向阀可以防止液压油回流,同时也起到稳定油压的作用。液压系统在工作时漏油明显,特别是在大压力加载时,因此,设置储能器以做油压补偿。
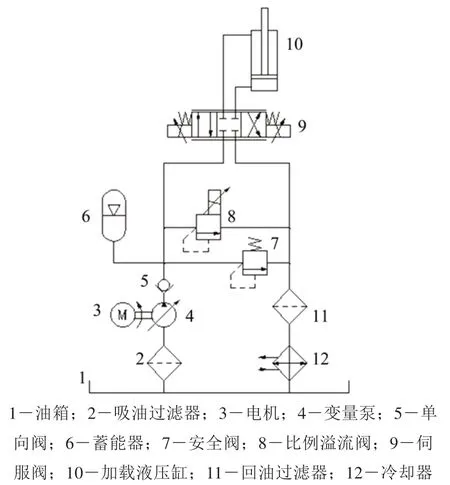
图2 液压系统液压回路图Fig.2 Hydraulic circuit diagram of hydraulic system
在进行车体静强度试验加载时,先将伺服阀工作于右位,液压系统中的电机驱动变量泵工作,变量泵输入的高压油充入加载液压缸无杆腔和蓄能器中,高压油使加载液压缸活塞杆伸出,加载液压缸活塞杆与枕木挤压,载荷作用于车体地板上产生竖直向下的力,实现车体的垂向加载。当加载力达到设定值,关闭电机以节省电能。此时,蓄能器中已充入高压油液,整个回路由蓄能器提供高压油液,进行漏油补偿和油压稳定。卸载时,将伺服阀置于左位,回路卸油,加载液压缸卸载,活塞杆收回,活塞杆与枕木脱离。由此,完成一次垂向加载试验。
2 数学模型
数学模型建模包括2部分:多点加载装置力学模型和液压系统数学模型。两者为各加载点加载力解耦提供了理论依据,为后续求加载力最优解和PID优化设计打下基础。
2.1 多点加载装置力学模型
为了解耦各加载点的加载力,即确定各加载点对支撑点的载荷贡献,本节依据上面设计的多点加载装置建立力学模型。
本文所提出的垂向液压加载系统共包含10个加载点,并通过10个对称的侧门将垂向力均匀地施加于地板上。因此,车体地板受力示意图如图3所示,图中,PL0,PL0,…,PL9为液压缸加载点,加载力竖直向下;PS0,PS1,PS2和PS3为支撑点,支撑力竖直向上。

图3 车体地板受力示意图Fig.3 Schematic diagram of car-body floor stress
定义垂直于地板竖直向下为力的正向。车体地板在加载过程中形变量和位移与车体长度和宽度相比很小,为简化模型,假设地板在有无加载力情况下均与地面平行,忽略地板受力后产生的形变量和位移。在该假设下,某一加载点加载力对支撑点的影响是线性的,即

式中:i=0,1,…,9,j=0,1,2,3;FLi为第i个加载点的加载力;FSji为第i个加载点的加载力对第j个支撑点的作用力,即加载点对支撑点载荷的贡献量;kji为FSji与FLi的比例系数。

式中:FSj为第j个支撑点的支撑力;FG为车体重力。
各支撑点的支撑力可表示为:

已定义垂直于地板竖直向下为力的正向,则车体地板竖直方向受力平衡方程为:

设xLi表示PLi与车体地板中心在x方向的距离;xSj表示PSj与车体地板中心在x方向的距离;yLi表示PLi与车体地板中心在y方向的距离;ySj表示PSj与车体地板中心在y方向的距离,由力矩平衡可得:

由式(3)~(13)可求得K,即每一加载点对支撑力的载荷贡献。
2.2 液压系统数学模型
液压系统采用四通伺服比例换向阀或变量泵控制液压缸油液压力,调节液加载压缸载荷。为简化液压系统模型,假设载荷调节仅由伺服阀完成,且伺服阀为零开口四边滑阀,液压缸同一容腔内各处压力相等;由于蓄能器的补偿作用,油源供油压力ps恒定,回油压力p0为0,忽略管路压力损失[9]。
则伺服阀的线性化流量方程可表示为:

式中:qL为加载液压缸流量;Kq为流量增益;xv为阀芯位移;Kc为流量-压力系数;pH为加载液压缸高压腔压力。
加载液压缸的流量连续性方程可表示为:

式中:Ap为加载液压缸活塞有效面积;xp为活塞杆位移;Ctp为液压缸总泄漏系数;Vt为加载液压缸总压缩容积;βe为油液有效体积弹性模量。
加载液压缸的力平衡方程可表示为:

式中:m为活塞杆等效质量;Bp为活塞杆粘性阻尼系数;Fo为加载液压缸加载力,同FL。
将上述方程进行拉普拉斯变换,可得:

由于黏性阻尼系数Bp较小,忽略Bp并进行简化,可得液压系统传递函数为

3 加载力求解与优化
本节建立多点液压垂向加载系统的软件模块。该模块主要分为2个部分:基于遗传算法的加载力最优寻解模块和基于PID的反馈调节模块。
3.1 遗传算法寻优
遗传算法在1962年由Michigan大学的Holland教授提出,它的机理主要是模拟自然界进化守则完成对目标对象的最优化处理。复杂非线性方程组最优求解问题是遗传算法能够解决的基本问题。遗传算法并行随机寻解的本质为解决多值模糊/半模糊方程组提供了条件,本文也是根据这一特点,利用遗传算法完成方程组半模糊求解,寻解最优加载力[10-12]。
设计目标是使静强度试验垂向载荷自定义分布,换言之,实现支撑点支撑力相等或可调。目前的研究难点在于各个加载点载荷对每个支撑点贡献未知,即难以确定加载力与支撑力之间关系。上一节建立的数学模型为加载力与支撑力关系提供了理论依据,加载力与支反力的关系可表示为:

式中:

方程的解不唯一。因此,这里运用遗传算法寻解最优加载力值。
遗传算法的求解步骤可简述为:初始种群定义及编码、建立约束和边界条件、遗传进化(选择、变异、交叉)、目标函数/适应函数评价、收敛终止。具体操作方法如下。
步骤1:确定寻优对象和编码方案。寻优对象为各加载点的加载力,因此,初始种群可设置为满足寻解收敛要求的一定数量种子加载力。遗传算法编码方式一般有二进制、十进制及浮点数编码等,本文选择采用二进制编码[13]。
步骤2:确定约束和边界条件。上一节各个支撑点支撑力与各个液压缸加载力之间的关系作为约束条件。另外,可增加边界条件:

步骤3:遗传算法寻解。详细操作和参数见案例中遗传算法参数表3。
步骤4:目标函数建立及适应值评价。本文采用方差评价计算加载力与目标加载力离散程度,建立目标函数,并以此作为适应值计算依据。以10个加载点的加载力为样本,则目标函数可表示为:

式中:σ2为样本方差;EF为样本数学期望。
步骤5:收敛终止。将每次遗传迭代出的计算加载力作为次代初始种群,重复步骤2~步骤4,直到适应值达到要求阈值或趋于稳定,得到的加载力为最优寻解。
3.2 PID优化控制
本节基于PID控制器反馈调节机制,整合软硬件配置,形成系统闭环控制回路,建立加载系统优化控制模型,如图4所示[14-17]。

图4 加载系统控制模型Fig.4 Control model of loading system
图中,s0~s9为遗传算法输出的目标加载力信号,i0~i9为伺服阀控制电流信号。整个闭环控制过程大体分为遗传算法计算后的初始加载和反馈优化后的调整加载。由于实际液压系统状态与数学模型表达的理想状态存在差别,因此,须在初次加载后,通过PID控制器的反馈机制进行调节,进行2~3次优化加载。首先,根据目标加载力和初始加载力,运用遗传算法控制器寻最优解,得到各液压缸加载力。然后,液压油源通过伺服阀向各液压缸提供高压油液,液压缸对各加载点产生载荷。此时,各加载点将力线性传递至各支撑点,支撑点产生实际支撑力。PID控制器采集各点实际支撑力,并与目标支撑力对比,遗传算法控制器再次计算加载力最优调整量,调整量转变为控制信号作用于伺服阀,调节液压缸加载力,最后,完成垂向载荷的最优加载。
4 算例
当该系统能够将均布的车体垂向载荷调节到任意目标载荷时,实现车体垂向载荷从非均布状态调节回均布加载将不是问题。因此,本文以均布载荷自主调节到自定义载荷为案例,证明本垂向加载系统设计的可行性。
本文以某一具有代表性的工况为案例,在MATLAB中进行仿真分析,并与实际加载值对比,验证所提出的加载系统及其自适应优化控制策略的有效性。所设计的垂向加载装置如图5所示。

图5 加载系统实物图Fig.5 Loading system
假设所设计的垂向加载系统初始加载力和实际加载值如表1所示,此时各加载力均匀分布且各支撑点支撑力相等。要实现垂向载荷的自定义加载,即各支撑点载荷不等,目标工况支撑力状态如表2所示。将目标工况代入遗传算法控制器,寻优加载力最优解,遗传算法计算参数如表3所示。计算过程中目标函数的适应值如图6所示。在迭代182次后,加载力值和适应值达到稳定,遗传算法达到停止条件。其中,平均适应值为2.72×109,最佳适应值为5.19×106。遗传算法输出结果如表4所示。

表1 仿真工况初始状态Table 1 Initial state of simulation
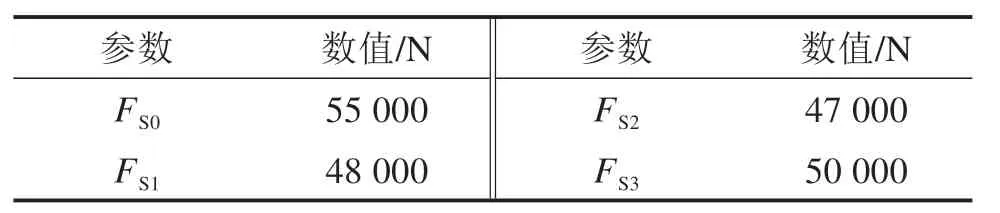
表2 仿真工况目标状态Table 2 Target state of simulation

表3 遗传算法参数Table 3 Parameters of genetic algorithm

图6 遗传算法适应值Fig.6 Fitness value of genetic algorithm calculation

表4 遗传算法输出结果Table 4 Output result of genetic algorithm calculation
将遗传算法控制器计算结果输入各PID控制器,调节伺服阀的加载力。通过仿真得到各支撑点的支撑力变化,如图7所示。由图7可知,系统经过约2.4 s达到稳定状态。

图7 支撑力变化情况仿真结果Fig.7 Simulation result of supporting force
仿真计算和试验实际系统各支撑点支撑力的稳态值对比如表5所示。仿真计算结果的支撑力稳态误差约为60 N,误差率约为0.13%,最大超调量约为425 N;现场试验实际结果与仿真结果偏差较小,试验支撑力稳态误差约为257 N,实际误差率仅为0.56%,好于传统沙袋加载的误差,满足试验误差要求。

表5 支撑力仿真与试验结果对比Table 5 Comparison of simulation and experiment results
5 结论
1)设计了一种基于自适应优化控制的轨道车辆车体静强度垂向加载系统,包括硬件加载装置、液压系统以及加载力控制软件模块,并通过试验验证其可行性。本文为较高准确度轨道车辆车体静强度垂向载荷加载系统的整体设计提供了重要参考,推动了车体静强度试验装备的自动化发展。
2)通过建立垂向加载系统力学模型和液控系统数学模型,确定各点加载力的耦合关系,为多点加载系统加载力解耦问题的解决提供理论依据。
3)该加载系统基于遗传算法,能够实现各点最优加载力快速寻解,为加载力最优解问题提供理论依据和解决思路。
4)将遗传算法与PID控制器结合,形成闭环控制系统,一方面能够实时反馈加载信息,另一方面,遗传算法的二次或多次寻优,即实现自适应优化控制,使垂向加载力最大限度接近期望值。本车体静强度垂向加载系统为该类试验装置实现加载力准确、可调和可控提供了一种设计思路。

