灾后交通网络修复与救援协同优化方法
秦进,杨康,徐玖龙,陈学伟
(中南大学 交通运输工程学院,湖南 长沙410075)
当今世界自然灾害频发,其破坏性威胁人类的生命安全,严重影响社会经济的发展,而紧急开展高效有序的应急救援行动,能够最大程度上减少人员伤亡和财产损失。由于应急救援行动通常具有时效性、突发性等特点,需要在短时间内对运送应急物资的救援队伍科学规划行驶路线。同时,必须兼顾路网节点损坏程度,修复顺序及受灾地区的物资需求量。如果未能在需求缓冲期间内将应急物资配送至指定地点,人们则会因为缺乏物资而产生焦虑、受冻、受饿等痛苦。因此,为了有效减轻救援期间内人们的痛苦程度,尽快满足受灾地区的物资需求,就必须对道路维修和物资运输路线结合考虑。近些年来,已经有许多国内外学者对灾后交通网络修复和救援协同优化问题进行了深入的研究和讨论。高学英[1]为应急救援资源布局及调度提供重要可行方法。程碧荣等[2]通过考虑服务时间窗和车辆装载能力等,保证救援关键期内应急物资供应不足下车辆路径合理规划。MAYA等[3]采用DP算法和GRASP元启发式算法解决灾后维修人员的调度和路径问题。ÇELIK[4]对有关网络重建和修复的文献进行全面的概述。WANG等[5]构建用于公路网恢复的双层编程模型,采用模拟退火算法与拉格朗日梯度投影法相结合进行求解。但在上述研究中,维修队伍与救援队伍的路径规划是分离的,导致维修队伍在不必经过或不紧急受损路段用很长的时间进行修复,使救援队伍在关键受损道路进行等候。因此,需要从系统的角度平衡两者之间的关系,减少等待时间。SHIN等[6]以时间长度最小化为决策目标,构建时空网络模型,确保在短时间内对紧急维修和救援的分配路线和时间表合理安排。ILOGLU等[7]提出对P中值问题的扩展,通过协调网络恢复人员和应急救援人员,使得紧急响应者在时间范围内与服务请求之间的累积加权距离最小化。SHIN等[6]将灾后救援队伍和维修车辆进行统一研究,建立综合调度模型。王晶等[8]以道路中断和可靠性下降来阐述灾后交通网络对物流配送的影响。现有的灾后应急救援路径选择文献的决策目标以最小化救援时间为主,而实际上,还需要更多地关注受难者在等待救济过程中承受的痛苦。HOLGUÍNVERAS等[9]将“剥夺成本”定义为人类因无法获得物资或者服务导致其痛苦所引起的经济价值,认为人道主义物流模型需要将福利经济原则考虑其中。ZHU等[10]以“相对剥夺成本”作为决策目标,更强调受难者承受的痛苦和救援公平性。SHAO等[11]对有关剥夺成本及其对关键问题讨论的最新文献进行回顾,分析当前剥夺成本的最新研究进展与研究成果。
1 问题分析及变量定义
自然灾害发生后,必须迅速开展应急救援预案,在确定受灾区域范围和交通网络受损状况以及物资需求量后,根据现有维修队伍和救援队伍的数量,以最小化受难群众累计产生的剥夺成本为目标,选择合理的路径优先修复受损节点,以保证救援队伍及时将应急物资输送至需求节点。由于途经的受损节点处在中断或者正在维修的状态,救援队伍无法通过,容易导致物资无法在短时间内运输至指定的需求节点,错过需求缓冲期,甚至有可能因为道路修复计划和物资运输路径的不协调,造成救援队伍在关键受损节点长时间等待,严重影响救援活动的开展。同时,由于受灾地点和受损节点较多且相对分散,救援队伍无法完全满足所有受灾地点在各自的需求缓冲期内将应急物资及时运送。因此,如何对有限数量的救援队伍和道路维修队伍进行协同调度,确定受损道路修复次序和应急物资运输路线,是灾后应急救援中必须首先解决的重大问题。
为了方便建立模型,定义变量如下:
V为节点集,Vd为需求节点集,Vr为受损节点集,E为路段集(i,j),∀i,j∈V,Er为受损节点对集合,W为救援队伍数量集合,∀w∈W,Z为维修队伍数量集合,∀z∈Z,so为初始起点,sd为虚拟终点,tij表示(i,j)的出行时间,∀i,j∈V,dij表示(i,j)的路程,∀i,j∈V,v表示队伍的行进速度,θ表示节点的损坏程度,θ=1,2,3,xiθ表示损坏程度为θ的情况下,节点i的修复时间,∀i∈Vr,x,i表示节点i的救济时间,∀i∈Vd,γi表示节点i的需求缓冲期,∀i∈Vd,qi表示节点i的需求量,∀i∈Vd,tarzi表示维修队伍z到达i的时间,∀i∈Vr,trzi表示维修队伍z修复i的时间,∀i∈Vr,tarwi表示救援队伍w到达i的时间,∀i∈Vd,trwi表示救援队伍w完成i的供给时间,∀i∈Vd,f2i表示i可访问的时间,∀i∈Vd,f′w表示救援队伍w完成救济服务的时间,∀i∈Vd。Ω+为救援队伍w到达之前产生的剥夺成本,Ω-表示救援队伍w到达之后产生的剥夺成本,Γiw表示救援队伍w完成i的供应后,在i累计产生的剥夺成本,∀i∈Vd,C表示所有需求节点的剥夺总成本。
另外,定义决策变量如下:


另外,结合实际情况,对问题做如下合理假设:
1)救援队伍在单次出行期间具有足够的供应能力。2)节点的损坏程度,修复时间以及路段间的距离是确定性的。3)节点之间若无连通路径,队伍均无法通过。4)队伍从同一起点出发,且行进速度相同。5)物资的需求量和需求缓冲期是确定性的。
2 模型构建
根据以上变量定义和问题描述,可以构建优化模型如下:
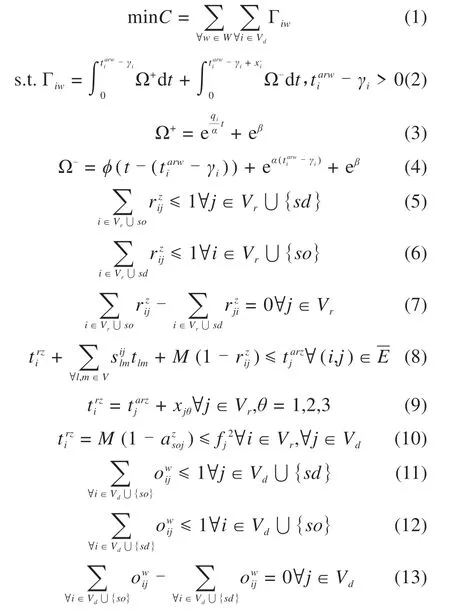
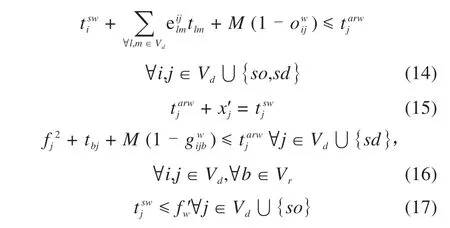
式(1)为目标函数,即总的剥夺成本最小化,其中的剥夺成本具体由式(2)~(4)计算。式(2)表示若从救援队伍w到达i的时间tarwj大于需求缓冲期γi时,Γiw为i累计产生的剥夺成本,反之Γiw=0。式(3)表示剥夺成本Ω+在等待救援队伍w到达之前呈现指数形式增长。式(4)表示剥夺成本Ω-在救济期间x'i,群众负面心理影响不会立即消失,而是以线性形式减少,直到完成救济后才完全消除。若tarwi-γi≤0,Γiw为0,即不产生剥夺时间成本。式(5)和式(6)表示确保每个受损节点i仅由维修队伍z修复。式(7)表示维修队伍z进入节点i完成修复任务后应离开该节点。式(8)是维修队伍z从已修复的i出发时间与从i到j的旅行时间之和,即达到节点j的时间tarzj。式(9)是维修队伍z∈Z完成节点j的修复时间。式(10)表示确保是在完全修复与需求节点相邻的节点i之后。式(11)和式(12)表示确保救援队伍w从i到j都仅服务一次。式(13)表示救援队伍w完成i的救援任务后应离开该节点。式(14)表示救援队伍w完成i供应后,到达j的时间tarwj。式(15)表示救援队伍w在j完成供应的时间tsjw。式(16)表示保证救援队伍w到j的到达时间tarwj不小于j的可访问时间f2j与相邻受损节点b到需求节点j之间旅行时间的总和。因此,救援队伍必须在最近的受损节点被修复之后才能访问需求节点。式(17)表示满足约束条件。
3 求解算法
本文提出了适用于该模型的二阶段蚁群算法[12]。第1阶段是对带时间窗的维修队伍进行路径规划,获得受损节点的修复顺序和修复时间。第2阶段根据修复方案对带时间窗的救援队伍进行路径规划,获得需求点的访问顺序和救济时间。每一种维修队伍的修复计划,救援队伍都能找到相对应的路径选择方案,根据救援方案的局部可行解判断其优劣性。重复上述步骤,更新和改进可行的解决方案以获得全局最优解。在该算法中,定义维修蚂蚁和救援蚂蚁。2种蚂蚁分别在各自的子网络图寻找可行的路径,可以有效地减少计算时间。本文采用Dijkstra算法确定蚂蚁行进路径的节点对是否存在于子网络图中,以便进行添加可行性检查。

4)救援蚂蚁y完成对所有需求节点的访问后,记录救援方案Uny,计算目标函数值Cy。若y=1,则令C0=Cy为初始目标函数值,令为初始救援方案。
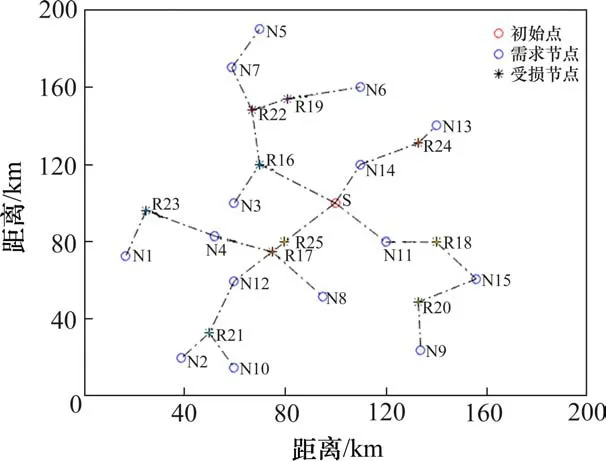
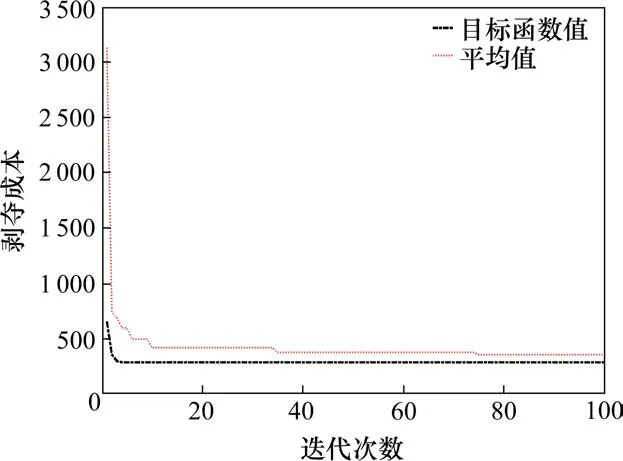
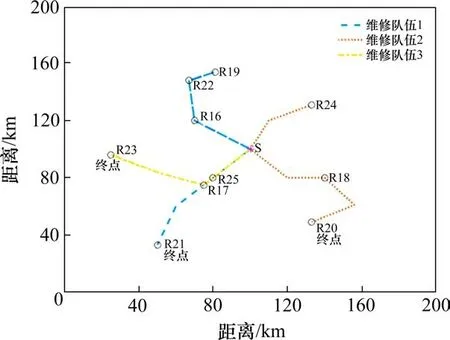
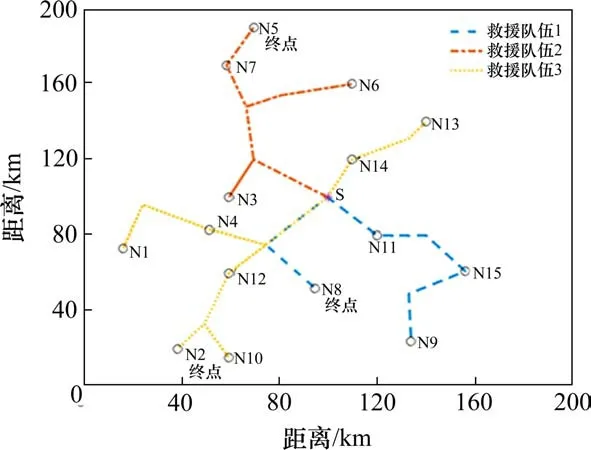
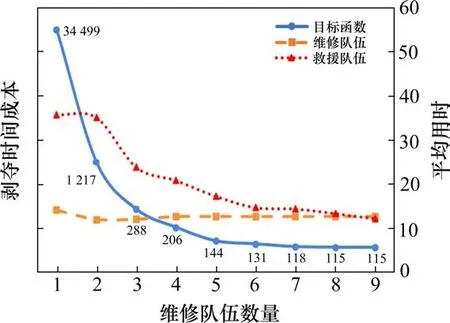
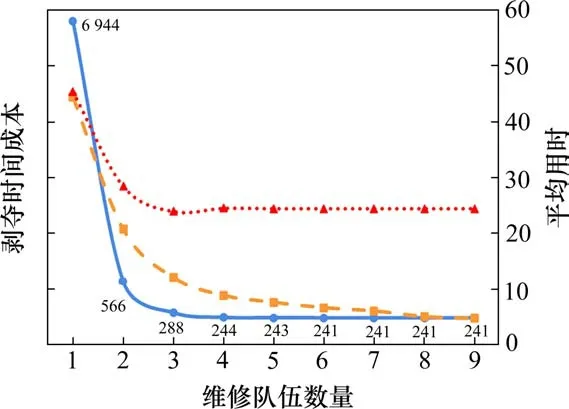
5)令y=y+1,若y Step 4令k=k+1,若k≤mr,重复步骤Step 2~Step 3;否则,转至Step 5。 Step 5信息素更新。采用带精英和排序混合策略更新信息素Δτr ij和Δτn ij。2种蚂蚁均根据目标函数值按从小到大依次排序,对排名λ位次的蚂蚁进行加权,并只考虑σ只精英蚂蚁数量。在排列中,前σ-1只蚂蚁中所经过的边获得信息素的量与该蚂蚁的排名位次成正比。此外,还采用精英策略,即到目前为止找出最优方案的蚂蚁所经过的边也将获得额外的信息素。在这样混合策略的设置中,信息素τr ij和τn ij根据下式进行更新: 表示σ-1只蚂蚁在节点对(i,j)之间根据排序对信息素的更新;如果第λ只最好维修蚂蚁经过(i,j),则Δτrλ ij=(σ-λ)Q/Cλ0,否则Δτrλ ij=0;同理可得Δτnλ ij=(σ-λ)Q/Cλ0,否则Δτnλ ij=0;如果(i,j)是找出最优解的边,Δτr*ij=σQ/C*0,否则Δτr*ij=0;同理可得Δτn*ij=σQ/C*0,否则Δτn*ij=0。其中:λ为蚂蚁排列的顺序号;Δτrλ ij与Δτnλ ij表示第λ只蚂蚁在路径(i,j)上信息素的增加量;Cλ0是第λ只蚂蚁的目标函数值;Δτr*ij和Δτn*ij是由精英蚂蚁在路径(i,j)上信息素的增加量;σ为精英蚂蚁的数量;C*0是当前最优值。 Step 6收敛性判断。若n 假设某地区发生灾害,救援中心共有1个供应点,其位置、维修队伍数量、救援队伍数量已知,如表1所示。有25个节点,包括15个需求节点,10个受损节点,其坐标及相关参数已知,如表2所示。受灾地区节点连接情况如图1所示。 图1 受灾地区需求节点与受损节点分布图Fig.1 Distribution of demand nodes and 表1 供应点位置坐标和队伍的数量Table 1 Supply point location coordinates and the number of teams 表2 节点坐标及相关参数Table 2 Node coordinates and related parameters 需求点间旅行时间如表3所示,受损点间旅行时间如表4所示。 表3 供应点与各个需求节点之间的旅行时间Table 3 Travel time/hour between supply point and each demand node h 表4 供应点与各个受损节点之间的旅行时间Table 4 Travel time/hour between the supply point and each damaged node h 本算例中,取救援队伍和维修队伍的行进速度v为30 km/h,常系数α和β分别为30和-1。在二阶段蚁群算法的求解过程中,目标函数的收敛情况如图2所示。随着迭代次数的增长,目标函数值和平均值均呈持续下降的趋势,在第5代时目标函数值收敛,C=287.8。此时3组救援队伍完成应急物资配送的时间分别为25.3,19.1和27.4 h。具体的路径方案如表5所示。 图2 目标函数值vs.迭代次数Fig.2 Objective function value and number of iterations 由表5可知,维修队伍的访问节点数量分别为4,3和3,完成修复时间分别为15,12.3和10.9 h,平均时间为12.7 h,完成修复时间相差较小。节点R21最后维修是由于N2和N10在救援过程中安排较后,因此节点R21同样被安排在较后的访问顺序中,维修队伍优先访问其他受损节点,如图3所示。同时,共有3组救援队伍均从初始点出发,访问节点数量分别为4,4和7,完成救援时间分别为25.3,19.3和27.4 h。节点N8分配给1号队伍并且最后一个访问,是由于该节点所需物资为2 t,与其他地区相比,需求量较少,且有较长的需求缓冲期,因此3号队伍可优先考虑对物资更加紧缺的需求节点,运输路线如图4所示。 图3 维修队伍路径方案Fig.3 Maintenance team path plan 图4 救援队伍路径方案Fig.4 Path plan of rescue team 表5 路径方案及时间窗Table 5 Route plan and time window 如图5所示,在维修队伍规模为3的情况下,救援队伍规模的扩大能够有效减少剥夺成本,表明救援队伍数量的增多加快物资配送的效率,以减少群众的负面心理影响。剥夺成本最终趋于稳定,是由于维修队伍数量有限,关键受损路段未能及时修复,部分救援队伍受阻。平均维修用时先降后升,最后趋于稳定,表明当救援队伍的数量少于或等于维修队伍的数量时,部分维修队伍为优先救援的需求节点所途经的受损节点进行修复,以减少救援队伍中途等待时间。由于救援队伍数量有限,规划路径下排序较后的需求节点需要等待,其余维修队伍在为这些需求节点所途经路线中受损节点维修的时间紧迫性小,但是随着救援队伍数量的增加,促使维修规划路径更合理化,维修计划用时缩短;当救援队伍的数量超过维修队伍的数量时,平均维修用时增大且维持不变,表明此时维修队伍的修复计划趋于合理化。 图5 不同救援队伍数量下目标函数及队伍平均用时情况Fig.5 Objective function and average team time under 如图6所示,在救援队伍数量为3的情况下,维修队伍数量的增加,促使多个受损节点同时进行维修,缩短了救援队伍等待的时间,使得剥夺成本和平均维修用时都在减少。平均救援用时有所上升,是由于每个需求节点存在需求缓冲期阶段,且需求量不一样,救援队伍在规划可连通路径时,更优先考虑需求节点的急需程度,而不是以救援时长最小为目的,平均救援用时趋于稳定表明救援路径方案已达到最优化;而维修队伍达到一定数量时,有部分停留在初始节点,处于待命状态,未参与维修工作,表明此时对该受灾地区中受损节点的修复能力已经达到饱和状态。 图6 不同维修队伍数量下目标函数及平均用时情况Fig.6 Objective function and average time consumption under 1)结合灾害发生后维修队伍和救援队伍存在协调欠缺而导致物资不能快速输送的特点,在假设受损节点的损坏程度及修复时间均为已知的前提下,同时考虑需求节点的物资需求量、救济时间以及需求缓冲期,以最小化累计产生的剥夺成本作为决策目标,构建了混合整数非线性规划模型。 2)设计出适用于该模型的二阶段蚁群算法,采用带精英和排序混合策略对信息素的更新进行改进,在提高解质量的同时,也加快了计算效率。最后,通过算例结果表明,维修队伍能够根据救援队伍的运输路径,优先对途经的关键受损路段进行修复,合理规划受损节点的修复次序,保证路网的畅通,减少救援队伍中途的等待时间。该方法具备合理性和可行性,能够为今后应急物流运输的相关决策提供有效的科学依据。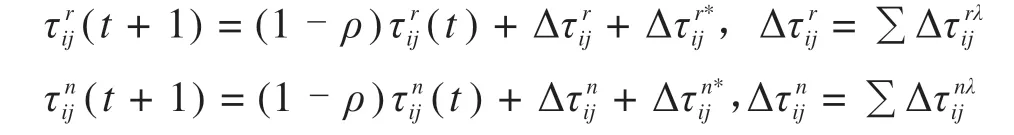
4 算例分析
4.1 算例简述

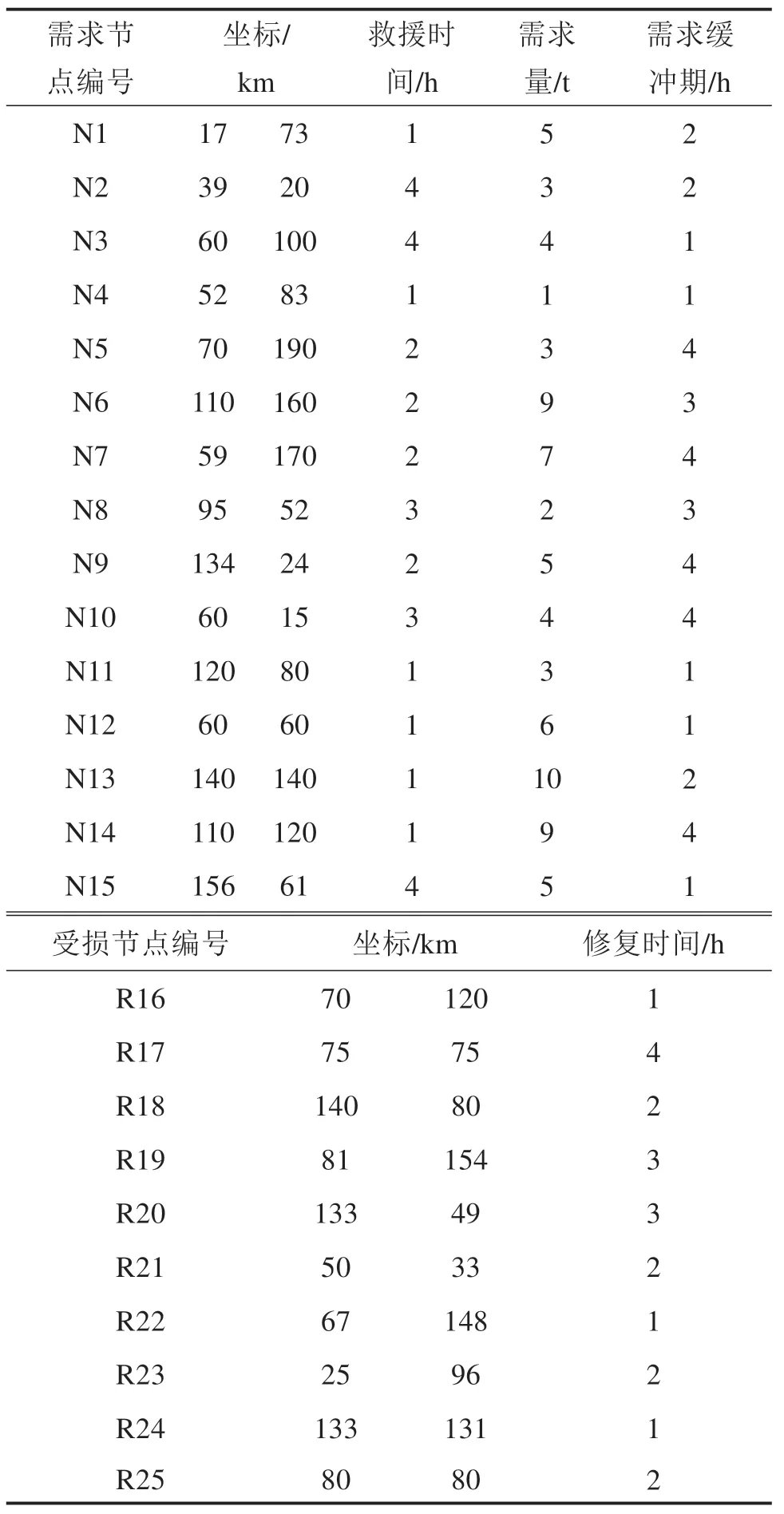
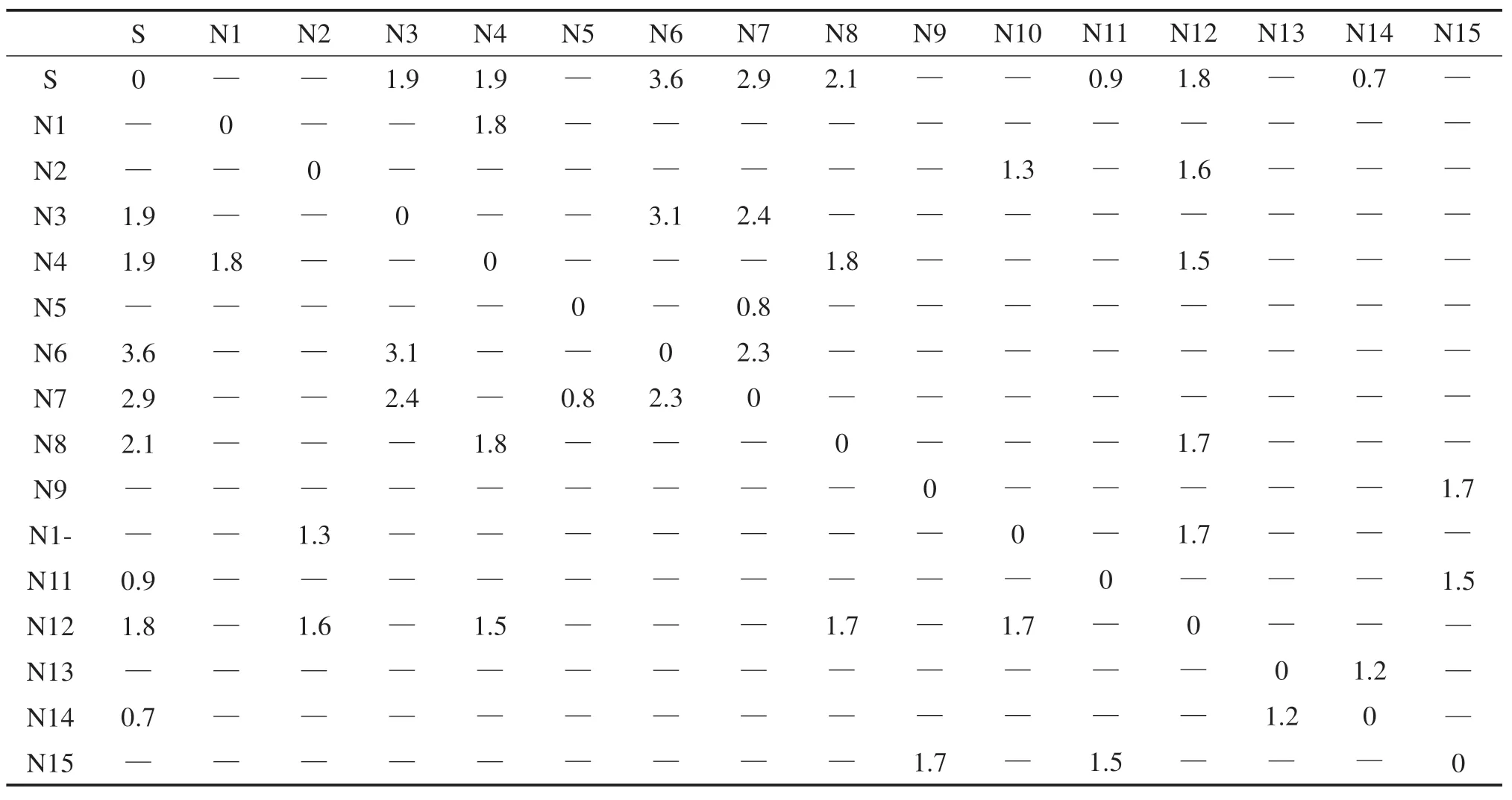
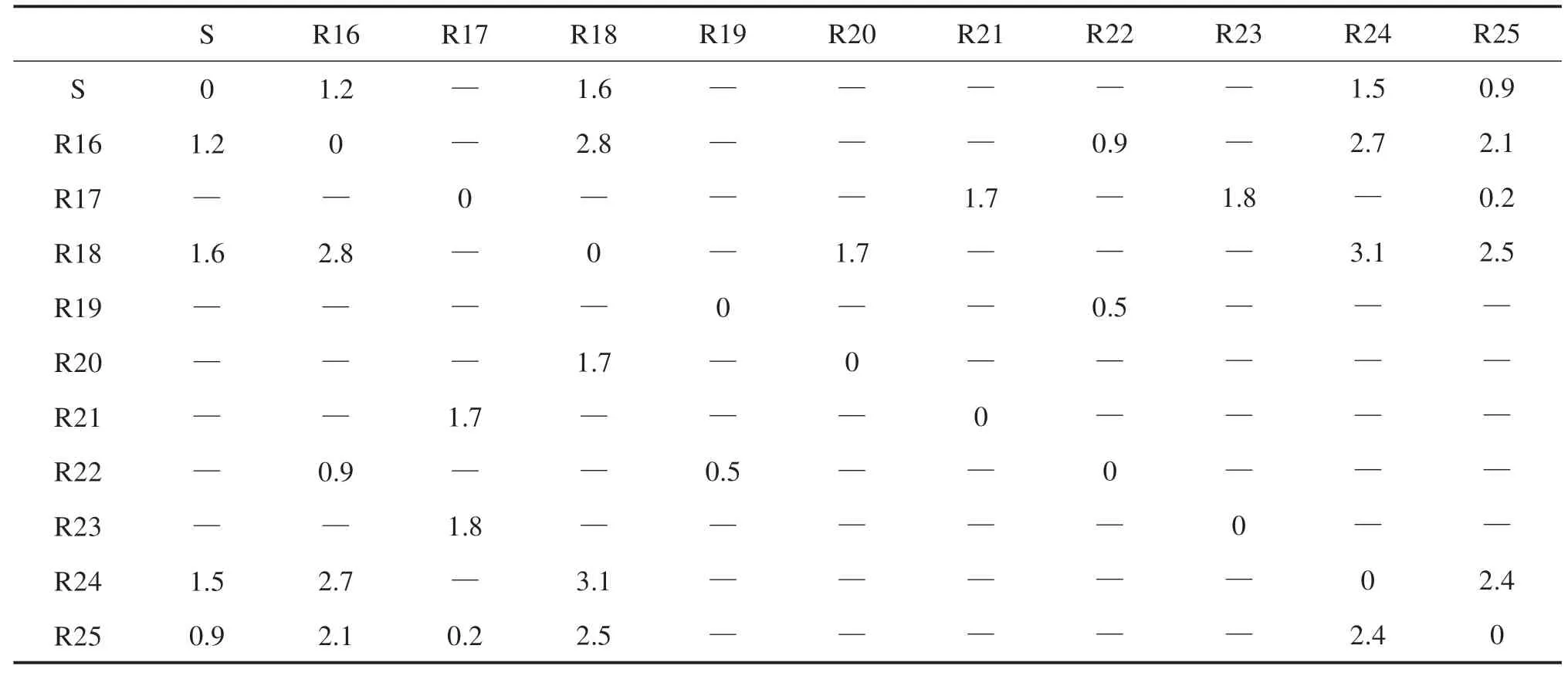
4.2 算例结果及分析

5 结论

