基于劳动力均衡的工程项目极限工期研究
彭军龙,王梦瑶,彭超,胡珂
(长沙理工大学 交通运输工程学院,湖南 长沙410114)
工程项目的施工工期始终是国内外建筑行业研究的重要内容。近年来,我国重大突发事件频发,而临时救援场所、道路桥梁恢复和应急医院等工程需要每一个建设者做出快速反应。由于事件的紧迫性,以新冠疫情下火神山医院与雷神山医院为例[1],举全社会之力提供大量资源在极限的工期内保质保量地快速建成。2座应急医院的建造速度令世界震惊,但是在大量人、财、物资源集聚,即资源宽容条件下,如何将项目的工期压缩到极限就变成了一个可研究的问题。目前,工程项目管理中,学者们研究主要集中在“资源约束−工期最短”[2-4],即在资源约束条件下,满足项目各工作间紧前紧后的关系,合理安排工作开始时间,使工程项目工期最短,这已被证明为NP-hard问题[5]。然而在国内新冠疫情及“十四五”规划中创新驱动发展[6]的背景下,从资源宽容这一新的视角,对工程项目的极限工期进行深入研究是十分必要的。研究过程中发现,即使资源宽容条件下,在管理[7-8]、技术[9-10]和环境[8,11]等方面,仍存在着许多影响项目极限工期实现的因素,而本文仅聚焦于有限工作面上劳动力均衡这一因素。这是因为在资源宽容条件下,由于工作面的限制,劳动力均衡也是影响项目极限工期实现的重要因素。基于此,本文引入劳动力均衡随机系数来衡量劳动力均衡的程度,建立以极限工期为目标的劳动力均衡模型,设计基于标准粒子群算法的模型求解方法,得到劳动力趋于均衡时工程项目的极限工期。
1 问题描述
1.1 问题假设
为了方便问题的研究,建立以下假设:
1)本文在资源宽容条件下实现项目的极限工期不影响工程项目的质量,并且为了求得极限工期的精确性,各工作的持续时间不取整,将其保留一位小数;
2)项目中各个工作的运行过程不可中断,且各个工作面上的工程量固定不变;
3)在资源宽容条件下,项目中各个工作面上劳动力分配量是相互独立的,不存在因劳动力缺失而导致某工作推迟或者无法按正常的计划进行;
4)当劳动力不均衡时,每个工作面上劳动力分配量大于或小于劳动力需求量相同单位量时对工期的影响程度相同。
1.2 符号定义
设某项目由工作V=[V0,V1,V2,…,Vn,Vn+1]组成,其中0和n+1分别表示项目的开始和结束,即表示不消耗时间和资源的2个虚工作,工作Vi(i=1,2,…,n)的持续时间和开始时间表示为di和si,且d0=dn+1=0;项目的工期T由虚工作Vn+1的开始时间sn+1表示;工作Vi中的劳动力总分配量、总需求量及产量定额分别为:Ri,Qi和Ei,其中Qi和Ei为常量;Ri为变量;工作Vi的工程量表示为Ci。
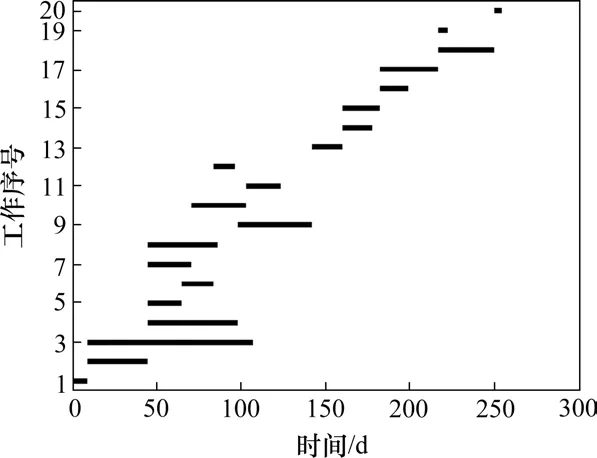
本研究中实现项目极限工期的目标是在有限的工作面上劳动力均衡的前提下,为了衡量工作面上劳动力均衡的程度,即劳动力的分配量与一定的需求量之间的偏差大小,本文引入劳动力均衡随机系数K。由于本文出现劳动力不均衡的2种情况为:Ri>Qi与Ri 其中:Ki为每个工作面上劳动力均衡随机系数,当Ki越来越接近1时,劳动力越来越均衡;当Ki=1时,即Ri=Qi时,劳动力完全均衡,达理想状态;zmax为大于1的常数,表示为能够接受的最大劳动力均衡随机系数。在有限的工作面上,考虑到安全距离及工作效率,本研究取zmax=1.5。 基于以上假设和分析,本文通过在有限的工作面上不断地优化调整劳动力的分配量,减少劳动力分配量与一定的需求量间的偏差,使资源量分配量与需求量趋于均衡,最终实现工程项目的极限工期。故模型的目标函数为式(2),T代表极限工期: 目标函数的计算步骤如下。 Step 1:根据有限工作面上能够接受的最大不均衡系数zmax,则符合劳动力分配方案的分配量应限制在2个已知常量最大值max Ri与最小值min Ri之间,其他方案不再予以考虑,则劳动力在工作i中的最佳总需求量为: Step 2:根据Qi与劳动力均衡随机数表达式(1)计算Ki。 Step 3:结合以上步骤计算工作的持续时间di。 Step 4:根据工作的持续时间,应用关键路径法,确定关键路径CP,求出工期sn+1。 约束条件为 其中:式(5)控制劳动力的分配量进行调整时不能超出范围,确保有意义优化;式(6)~(7)工程项目中各个工作的持续时间与劳动力非负约束。 粒子群算法(Particle Swarm Optimization,PSO)是由EBERHART等提出的一种仿生进化算法[12],被证明其具有简便、易实现和鲁棒性好等优点[13-14]。由于本文所要研究的问题,在资源宽容条件下,通过解决项目中各个有限工作面上的劳动力均衡,从而实现工程项目极限工期,本质上属于工期优化问题。因此,本文基于标准粒子群法,通过对进化方程及惯性权重参数进行改进,设计出符合本研究模型相应的求解算法,最终有效地解决本研究劳动力均衡时工程项目极限工期的问题。 在资源宽容条件下,本文建立的以极限工期为目标的劳动力均衡模型。假设目标问题的N维可行解搜索空间中有M个粒子,其中:N代表该问题中的工作数目,M代表粒子群规模大小,即粒子个数。粒子i当前飞行速度表示为Vi(t)=(vi1,vi2,…,viN);粒子i当前位置表示为Xi(t)=(xi1,xi2,…,xiN),是该目标问题的一个可行解,其中xij(i=1,2,…,M;j=1,2,…,N)的值对应工作的实际劳动力分配量。粒子i下一个时刻的速度Vi(t+1)取决于当前速度Vi(t),自身最佳位置Pi(t)与全局最佳位置Pg(t),该粒子经过速度更新移动到下一个位置Xi(t+1),粒子在空间中的位置移动机制如图1所示[14]。[xjmin,xjmax]为粒子在空间j维上的活动范围,xjmin表示工作i最小劳动力分配量,xjmax表示工作i的最大劳动力分配量。粒子在搜索空间上不断地优化更新,逐步达到粒子的最佳位置,即项目各个工作面上的最佳劳动力分配方案,此时的适应度值为优化后的极限工期。 图1 粒子在空间中的位置移动机制Fig.1 Mechanism of particle movement in space 在对粒子群算法进化方程进行改进时,本文从实际工程项目的角度出发,一个工程中劳动力的数量要求为整数,那么xij所对应工作面上劳动力实际的分配量应为一个整数。因此,调整后的进化方程为: 式中:ω是惯性权重值;c1和c2是自身认识学习和社会学习的2个速度因子;r1和r2是2个随机数,一般在[0,1]区间中取值;t=1,2,…,G是迭代次数,而G是最大的迭代次数。 通过式(8)~9)进行速度与位置更新,即不断调整劳动力的分配量,以达每个工作面上劳动力趋于均衡。 由于标准的粒子群算法中的ω为固定值,很可能出现粒子早熟而导致局部最优的现象。因此,为了提高算法对该研究模型的求解精度和收敛速度,本文采用动态ω。该动态ω是由文献[15]在引入聚焦距离变化率概念并将其定义的基础上,对惯性权重进行动态调整,即: 式中:k是聚焦距离的变化率;MaxDi st是最大的聚焦距离;Mean Dist是平均的聚焦距离;r是[0,1]区间内均匀分布的随机数;一般取α1=0.3,α2=0.2。 综上所述,本文针对以极限工期为目标的劳动力均衡模型设计的算法流程如下。 1)算法执行前准备工作:输入目标函数及约束,读取案例各工作的数据,设置该算法的各项参数; 2)初始化和适应度值计算:根据项目的具体情况,对所有粒子的速度与位置初始化,形成一个初始矩阵; 3)迭代进化更新:在式(10)~(11)的基础上得到动态惯性权重ω,根据进化更新公式(8)~(9)对群体中所有粒子进行速度与位置更新,并计算此次迭代后的适应度值; 4)评价粒子判优劣:每次进化迭代后,对各粒子的适应度值进行比较,得到pi与pg,进入下次迭代; 5)迭代终止条件设置:当迭代次数满足最大迭代次数G时,则终止算法进程,最终输出结果T(pg b est),Ri,di和Ki;否则,转3)继续迭代; 6)结束。 具体求解流程如图2所示。 图2 改进的粒子群算法求解流程Fig.2 Improved PSO solution flow 以某段公路工程项目为例,共有20个工作,合同工期为350 d。由于每个工作的计量单位不同,并且大部分工作又包含多个具体施工内容,所以为了方便研究,现将各项工作的工程量抽象为无计量单位的综合工程量,对应的人工产量定额为综合人工产量定额。根据各项工作间逻辑关系,绘制了网络计划图,如图3所示,各项工作的相关参数如表1所示。 表1 各项工作相关参数Table 1 Work-related parameters 图3 项目双代号网络计划图Fig.3 Project double generation network plan 在MATLAB R2017b环境下,本文导入实例的相关数据,并对基于改进粒子群算法的模型求解流程进行编码。初始参数设置如下:搜索空间维数为N=20;种群的规模为M=50;初始惯性权重设置为:ωmax=0.95,ωmin=0.25;学习系数c1=c2=2;最大迭代次数G=200。算法运行50次,结果如表2所示。 迭代结果可知,该项目极限工期为253.26 d,相较于合同工期提前了27.64%。此时该项目的关键线路为①→②→③→④→⑧→⑩→○12→○15→○16→○17→○18,对应的进度计划横道图如图4所示。 图4 项目进度计划横道图Fig.4 Bar chart of project schedule 在各项工作不均衡系数Ki的基础上得到了均衡性偏差ΔKi,具体数据如表2所示。除了人机配合的工作外,均不超过0.100,表明各项工作劳动力趋于均衡的基础上实现项目极限工期。因此,得到的项目最佳人工分配方案及极限工期具有较好的可靠性。此外,求解过程是逐步收敛,大约25代以后已经保持收敛达到最优解,验证了模型和算法解决工程项目实际问题的可行性。 表2 计算结果Table 2 Calculation results 为进一步验证改进粒子群算法的优越性,使用标准的粒子群算法,再次对同一个案例进行模拟仿真,参数设置与本文改进的粒子群算法一致。2种算法的性能对比表及进化曲线对比分别如表3与图5所示。 图5 算法进化过程对比Fig.5 Comparison of evolutionary processes 表3 算法对比结果Table 3 Comparison results 试验结果表明,本研究针对模型改进粒子群算法的求解结果及计算效率较优于标准的粒子群算法:在目标函数值方面,改进粒子群算法求得的极限工期为253.26 d,少于标准粒子群算法的256.49 d,精确性较强;在收敛速度方面,具有动态惯性权重的粒子群算法在25代保持收敛达最优解,比标准的粒子群算法收敛速度快了5.2倍,效率较强。由此可见,本文提出改进粒子群算法在实际案例求解时表现出明显的优越性。 1)引入的劳动力均衡随机系数,通过衡量有限工作面上劳动力均衡程度,能够有效地对劳动力进行优化调整,减少劳动力分配量与一定需求量之间的偏差,使劳动力趋于均衡。 2)在实际工程项目仿真中,建立的以极限工期为目标的劳动力均衡模型以及模型求解算法,能够获得最佳劳动力分配方案的基础上实现项目的极限工期。模拟仿真结果不仅验证了该模型的简单可操性,也表明了具有动态变惯性权重的粒子群算法在进行模型求解的过程中,搜索精度及效率较高。 3)本研究结果不仅丰富了工程项目极限工期相关理论,而且为管理者实现工程项目极限工期提供了及时的科学依据。在未来研究中,将全面考虑资源宽容条件下影响项目极限工期的其他因素,以期综合效应下进一步追求项目的极限工期。
1.3 模型建立—以极限工期为目标的劳动力均衡模型
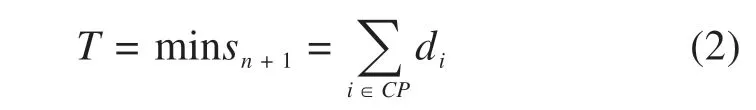



2 模型求解的算法设计
2.1 编码方案

2.2 粒子群算法进化方程的改进

2.3 惯性权重ω的参数改进

2.4 模型求解的算法步骤

3 算例分析
3.1 工程项目案例


3.2 算例求解结果

3.3 求解结果与计算效率对比分析


4 结论

