大跨桥上减振轨道过渡段动力特性分析

骆婷，韦凯，王显，马宏辉，王平

(西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都610031)

随着高速铁路建设的不断推进，我国现代大跨度铁路桥梁技术得到了广泛的运用，目前已经建成的高速铁路桥梁最大跨度可达630 m[1]。与中小跨度桥梁相比，列车荷载作用下大跨桥自身的挠曲变形更容易使无砟轨道层间出现离缝、脱空等现象。然而，既有工程经验表明，在无砟轨道层间铺设橡胶垫层可保证轨道结构与桥梁之间变形协调，减少此类病害的出现。因此，大跨桥无砟轨道需要进行缓冲垫层设计。另一方面，普通轨道与减振轨道之间存在较大的刚度差异，列车通过具有刚度差异位置处会激起较大轮轨冲击力。在列车长期运营下，使得轨道表面不平顺进一步恶化，导致乘客舒适度下降，严重时导致轨道结构产生疲劳破坏，甚至威胁行车安全。因此，有必要在减振轨道进行过渡段设计。在一些过渡段技术文献中，描述了轨道过渡段的设计和补救措施，提出如逐渐改变轨枕长度和间距、采用附加钢轨和扣件系统等技术措施[2-6]。但这些措施主要为了解决路基与桥梁、桥梁与隧道、有砟−无砟轨道之间等两侧刚度差异不明显的传统过渡段问题。对于普通轨道与减振轨道之间的过渡，轨道两侧刚度差异明显，同时考虑到大跨桥自身挠曲变形的影响，显然，传统的过渡方法已经不适用于这种情况。随后，一些学者通过分析过渡段轨道的动力特性对其过渡方式进行了若干研究。周文涛等[7]建立列车-CRTSⅡ轨道−路基(桥梁)仿真模型，对路桥过渡段的动力响应进行分析，提出过渡段车体和轨道动力响应指标随着不均匀沉降差、轨面折角的增大而增大，建议不均匀沉降差不超过5 mm，轨面折角不超过1‰，但该文献未考虑轨道刚度差异对过渡段的影响。雷晓燕等[8-9]为明确轨道刚度突变对过渡段动力特性的影响，分析路基刚度突变时轨道过渡段的动力响应，提出刚度突变会使钢轨垂向加速度、轮轨作用力等指标出现峰值，从而形成冲击作用。若同时考虑轨道不平顺的存在，动力响应增幅更明显。李成辉等[10]从线路动不平顺的角度出发，研究有砟−无砟轨道过渡段的轨下刚度与动不平顺的关系，提出轨下刚度线性过渡方式最佳；若采用分段式过渡，分段数不得少于5段，且过渡段的长度宜结合车速设置为20～30 m；任娟娟等[11]建立了列车-轨道-路隧过渡段垂向耦合动力分析模型，对路隧过渡段动力特性进行分析，提出过渡段处形成的刚度差主要影响钢轨的挠度变化，建议过渡段采用刚度分级的过渡方式，相邻2级轨道板刚度比不大于2；XIN等[2]采用自编程序，建立车辆-轨道耦合动力学模型，研究了固定板式轨道−浮置板板式轨道过渡段的动力学性能，讨论采用橡胶垫逐渐改变刚度来解决过渡问题可行性，提出并优化了一种5板过渡方案。刘钰等[12]分析有砟轨道轨下胶垫刚度、枕下胶垫刚度、有砟轨道轨枕类型、道砟胶结、辅助轨等因素对有砟−无砟轨道过渡段动力学特性的影响，综合分析过渡段各种轨道结构部件的刚度合理匹配关系。以上研究虽然分析了刚度差对过渡段动力响应的影响，但更多针对于传统的过渡段问题，对于大跨桥减振轨道过渡段的研究较少。然而，在列车荷载作用下，大跨桥梁会产生挠曲变形，这种挠曲变形是否会对过渡段设计产生影响，现有针对传统过渡段刚度差提出的过渡段设计是否适用于桥上减振过渡段还值得进一步的探讨。因此，为了对此类过渡段设计的安全性进行合理评估，本文建立高速列车-无砟轨道-大跨桥刚柔耦合动力学模型，分析考虑和未考虑大跨桥挠曲变形时减振轨道过渡段的动力响应，明确大跨桥梁挠曲变形对桥上过渡段动力特性的影响，并在此基础上，分别研究橡胶垫层刚度、过渡段长度等因素对该过渡段动力响应的影响，提出针对大跨桥减振轨道过渡段合理的设计方案。研究结果以期为我国高速铁路大跨桥上减振轨道过渡段设计提供参考方案。

1 工程概况

1.1 桥梁概况

某在建高速铁路大跨桥无砟轨道中，大跨桥采用97 m+240 m+97 m的钢桁梁−拱组合桥。其中，主桁架采用三角形桁架，桁高、桁宽为14 m，节间长度为12 m；拱轴线采用圆弧线，半径为165.3 m；桥梁主体采用正交异型整体钢桥面板和现浇混凝土垫层，垫层厚度为25 cm。97 m+240 m+97 m的大跨度钢桁梁-拱组合桥纵断面图具体如图1所示。

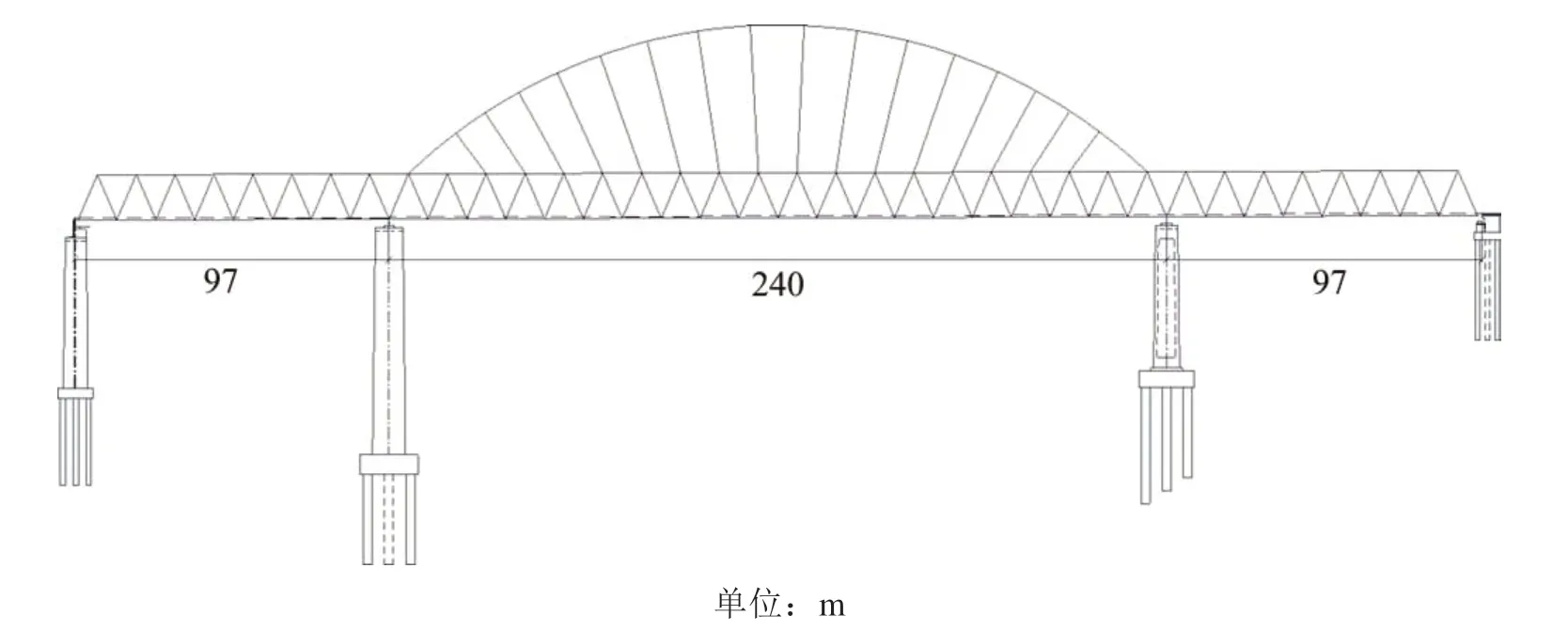
图1 大跨度桥梁纵断面图Fig.1 Longitudinal section of long-span bridge

1.2 无砟轨道概况

桥上无砟轨道采用CRTS I型双块式无砟轨道结构，轨道结构自下而上主要由桥面保护层、抗剪凸台、底座板、中间层、道床板、双块式轨枕、WJ-8B型扣件系统以及60 kg/m钢轨组成，具体如图2所示。按轨道类型分，桥上无砟轨道主要可分为普通轨道和减振轨道2种，其中大跨桥主跨为中间层铺设14 mm橡胶垫层的减振轨道，边跨为中间层铺设4 mm聚丙烯纤维土工布的普通轨道，普通轨道与减振轨道之间设置过渡段，过渡段无砟轨道结构中间层也采用14 mm橡胶垫层，但其刚度与减振轨道橡胶垫层刚度不同。同时，因轨道类型不同，道床板的尺寸也有所差异，具体见表1。

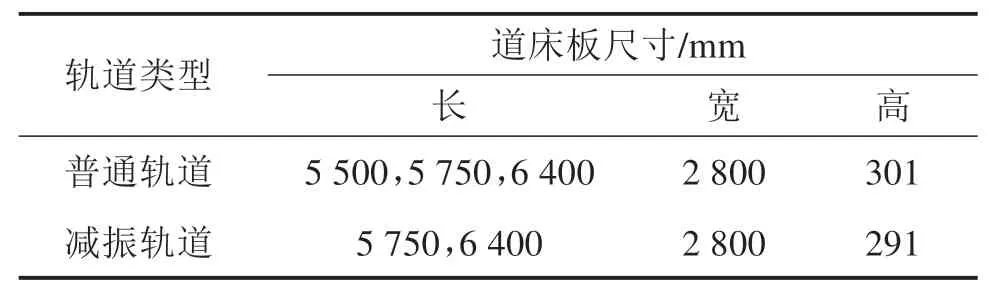
表1 道床板类型Table 1 Type of track plate

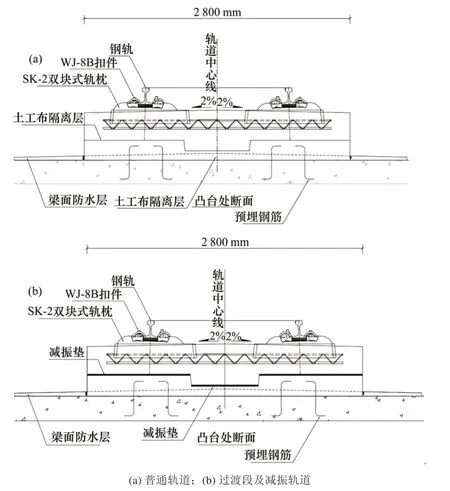
图2 大跨桥上CRTS I型双块式轨道结构Fig.2 CRTS I double block track structure on long span bridge

2 模型建立

2.1 车辆模型

车辆可视为由车体、转向架、轮对组成的多刚体系统。其中，车体与转向架之间、转向架与轮对之间分别通过二系悬挂结构、一系悬挂结构连接。本文参照CRH380B型列车基本参数[2]，不考虑刚体伸缩，采用多刚体动力学软件自带车辆模块建立具有35自由度的车辆模型。车辆模型如图3所示。

图3 高速列车模型Fig.3 High-speed train model

2.2 无砟轨道-大跨桥模型

根据设计资料，利用有限元软件建立无砟轨道-大跨桥有限元模型。其中，道床板、底座板与桥梁桥面采用实体单元模拟，钢桁架与拱部分采用梁单元模拟，钢轨、桥墩墩台部件分别采用多刚体软件中自带的柔性轨道模型、Base 0刚体模拟，而桥梁与底座板之间、桥梁与桁架拱之间设置绑定约束，钢轨与道床板之间的扣件系统、底座板与道床板之间的橡胶垫层以及桥墩对桥面的支承作用采用多刚体软件自带的bushing力元，通过设置不同的力元参数进行模拟。模型采用的各结构部件参数如表2所示，有限元模型如图4所示。

图4 有限元模型Fig.4 Finite element model

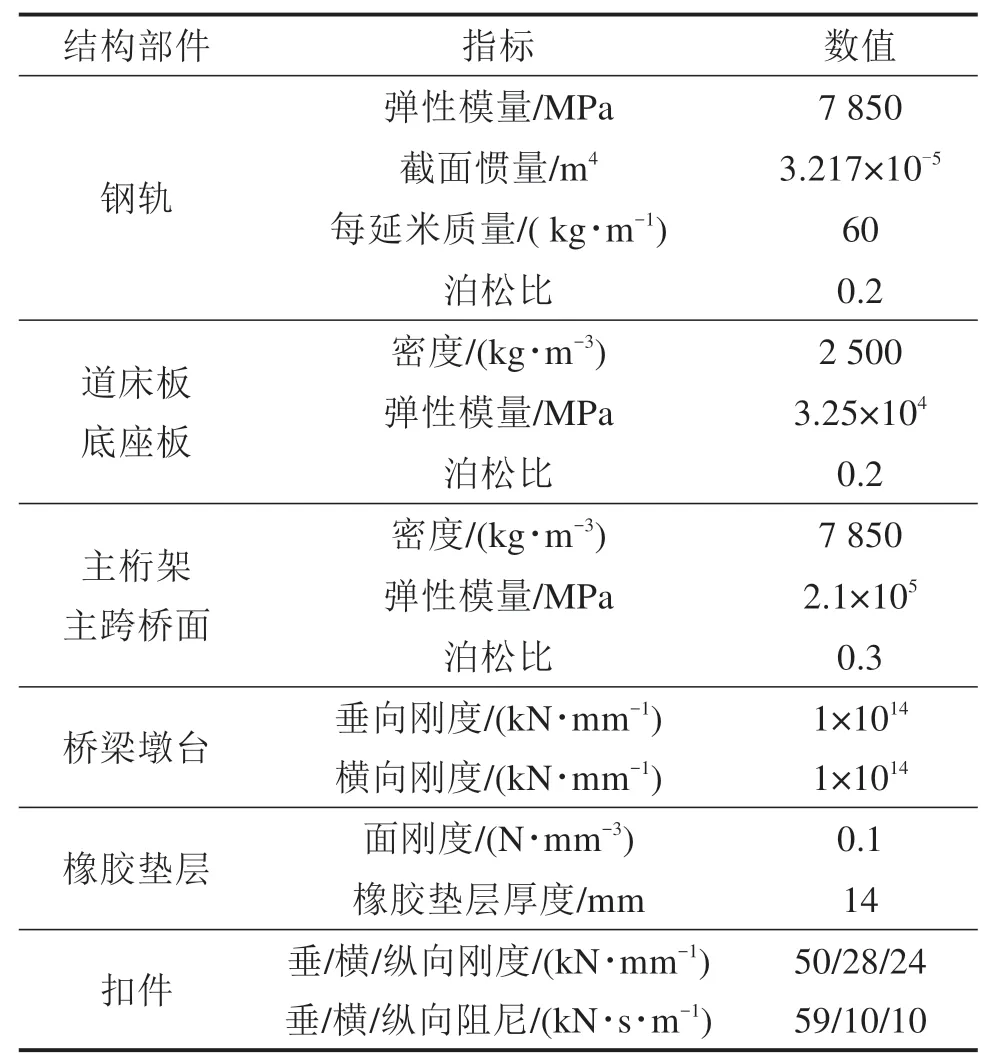
表2 各结构部件参数Table 2 Parameters of each structural component

有限元模型建立之后进入后处理模块进行模态分析，并通过ABAQUS-UM接口将有限元模型的几何、质量、刚度、模态以及节点坐标信息文件导入多刚体软件中与车辆模型进行刚柔耦合。

2.3 轮轨接触关系

本文基于经典的Hertz非线性弹性接触理论，计算得出的轮轨接触法向力满足：

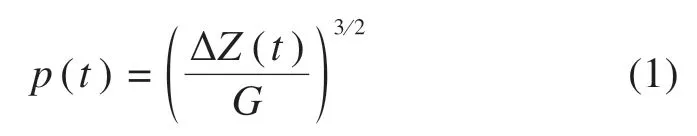
式中：ΔZ(t)为t时刻轮轨之间的弹性压缩量，m；G为轮轨接触常数，m/N2/3，与车轮踏面有关。

当存在轨道不平顺Z0(t)时，ΔZ(t)的计算公式如式(2)所示：

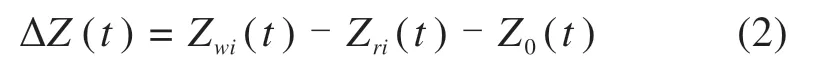
其中：Zwi(t)为车轮位移，m；Zri(t)车轮接触点处的钢轨位移，m。

车轮踏面采用磨耗型踏面，因此，轮轨接触常数G计算公式满足：

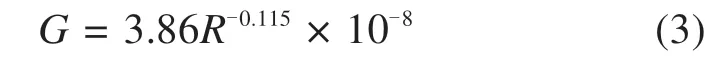
2.4 模型验证

为了验证模型的准确性，本节进行钢桁梁-拱组合桥的模态分析，提取桥梁前5阶模态，并与文献中类似桥梁结构的模型进行比较，具体如表3所示。从表3中可以看出本文有限元模型频率较文献[13]的频率相差不大，且振型相似。因此，表明计算模型可以真实反映大跨桥的动力特性。

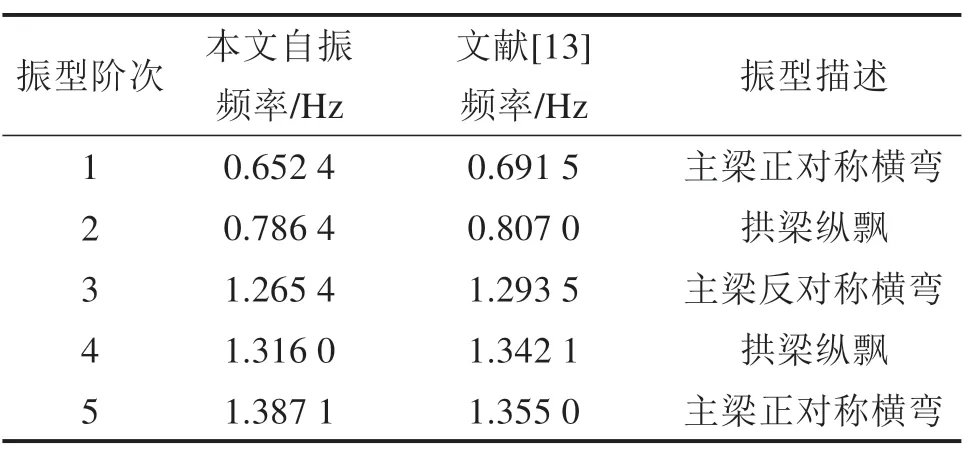
表3 桥梁自振特性Table 3 Natural vibration characteristics of bridge

3 过渡段动力特性分析

3.1 动力学评价指标的选取

由于轨下基础刚度突变会导致刚度突变处产生轮轨力冲击，因此，在进行轨道刚度过渡段设计和评估时须采用动力学评价方法。文献[14]通过动力学分析指出钢轨挠度变化率(钢轨动挠度曲线的斜率)是作为有效评价轨下基础刚度差引起的轮轨动力作用以及过渡段长度影响的综合指标，且当钢轨挠度变化率控制在0.3 mm/m以内时，可以保证轨道过渡段具有良好的动力学性能[15]。因此，为了准确分析、评价高速列车过桥时大跨桥上减振轨道过渡段的动力特性，本文参照《高速铁路工程动态验收技术规范》(TB 10761—2013)[16]，选取轮轨垂向力、车体加速度、钢轨挠度变化率等作为过渡段设置效果的评价指标。各动力学评价指标限值见表4。

表4 动力学评价指标限值Table 4 Limits of kinetic evaluation indexes

3.2 大跨桥梁对过渡段动力特性的影响

由于列车荷载作用下大跨桥自身的挠曲变形可能会对桥上过渡段的动力特性产生一定的影响，因此，在进行大跨桥减振轨道过渡段动力特性分析之前，首先要明确大跨桥挠曲变形对动力学评价指标的影响。本节设计2组对比工况，即不考虑大跨桥挠曲变形与考虑大跨桥挠曲变形的过渡段工况，分析大跨桥挠曲变形对于桥上减振轨道过渡段动力特性的影响规律。为了模拟线路实际运行的状态高速列车采用16节编组的CRH380B型列车动车组，设计时速为350 km/h。同时，考虑到桥梁两端一定长度的影响，动车组首车距桥30 m，且为使影响因素单一化，此处不考虑轨道不平顺的作用。2组对比工况的计算结果如图5所示。

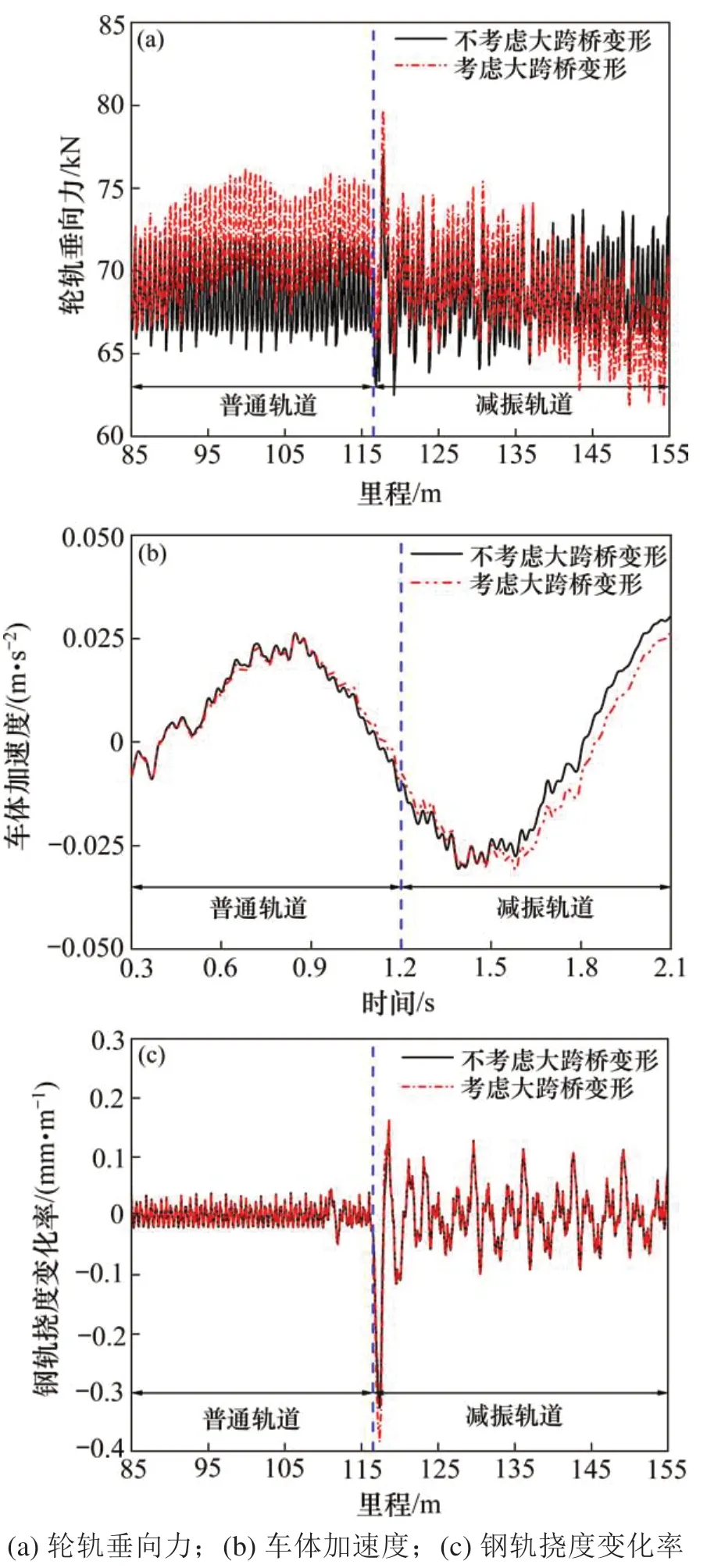
图5 大跨桥对动力学评价指标的影响Fig.5 Influence of long-span bridge on dynamic evaluation index

由图5可知，大跨桥挠曲变形主要对钢轨挠度变化率的影响较为显著，对轮轨垂向力、车体加速度的影响较小。其中，与不考虑大跨桥挠曲变形的工况相比，考虑大跨桥挠曲变形时过渡段的最大轮轨垂向力、最大车体加速度分别为79.7 kN，0.03 m/s2，变化幅度均较小，可忽略不计。但考虑大跨桥挠曲变形的钢轨挠度变化率峰值可达到−0.383 mm/mm，较不考虑大跨桥挠曲变形的钢轨挠度变化率峰值增大了17.8%。因此，大跨桥挠曲变形对桥上减振轨道过渡段动力响应的影响不容忽视。

3.3 橡胶垫层刚度对过渡段动力特性的影响

由于减振轨道铺设的橡胶垫层刚度越小，普通轨道与减振轨道连接处的刚度差越大，该连接处的钢轨挠度突变值越大，从而产生的动力响应可能越强。因此，为了明确橡胶垫层刚度对过渡段动力响应的影响，本节先研究大跨桥上减振轨道橡胶垫层刚度不同时，大跨桥上普通轨道与减振轨道连接处两侧的刚度差对轮轨垂向力、车体加速度以及钢轨挠度变化率的影响，再在此基础上提出过渡段橡胶垫层刚度合理的布置方式和取值。

3.3.1 过渡段刚度差对其动力特性的影响

本节选取4种不同的橡胶垫层刚度工况进行计算。其中，橡胶垫层面刚度分别为0.1，0.15，0.2，0.5 N/mm3。通过仿真计算，可得列车通过大跨桥减振轨道过渡段时，过渡段动力学评价指标在不同橡胶垫层刚度下的变化情况。仿真后的过渡段动力响应如图6所示。

由图6(a)和6(b)可知，该连接处存在的刚度差会使轮轨垂向力和车体加速度发生突变，但突变值较小。其中，减振轨道铺设的橡胶垫层刚度越小，该连接处存在的刚度差就越大，轮轨垂向力和车体加速度的突变值也就越大。当橡胶垫层面刚度为0.1 N/mm3时，其连接处的轮轨垂向力和车体加速度峰值达到最大，最大轮轨垂向力为79.7 kN，远小于规范中的规定限值170 kN；最大车体加速度为0.030 m/s2，远小于规范中的规定限值。说明当列车通过大跨桥上普通轨道与减振轨道连接处时，该处的刚度差对行车安全性和乘客舒适性的影响有限。

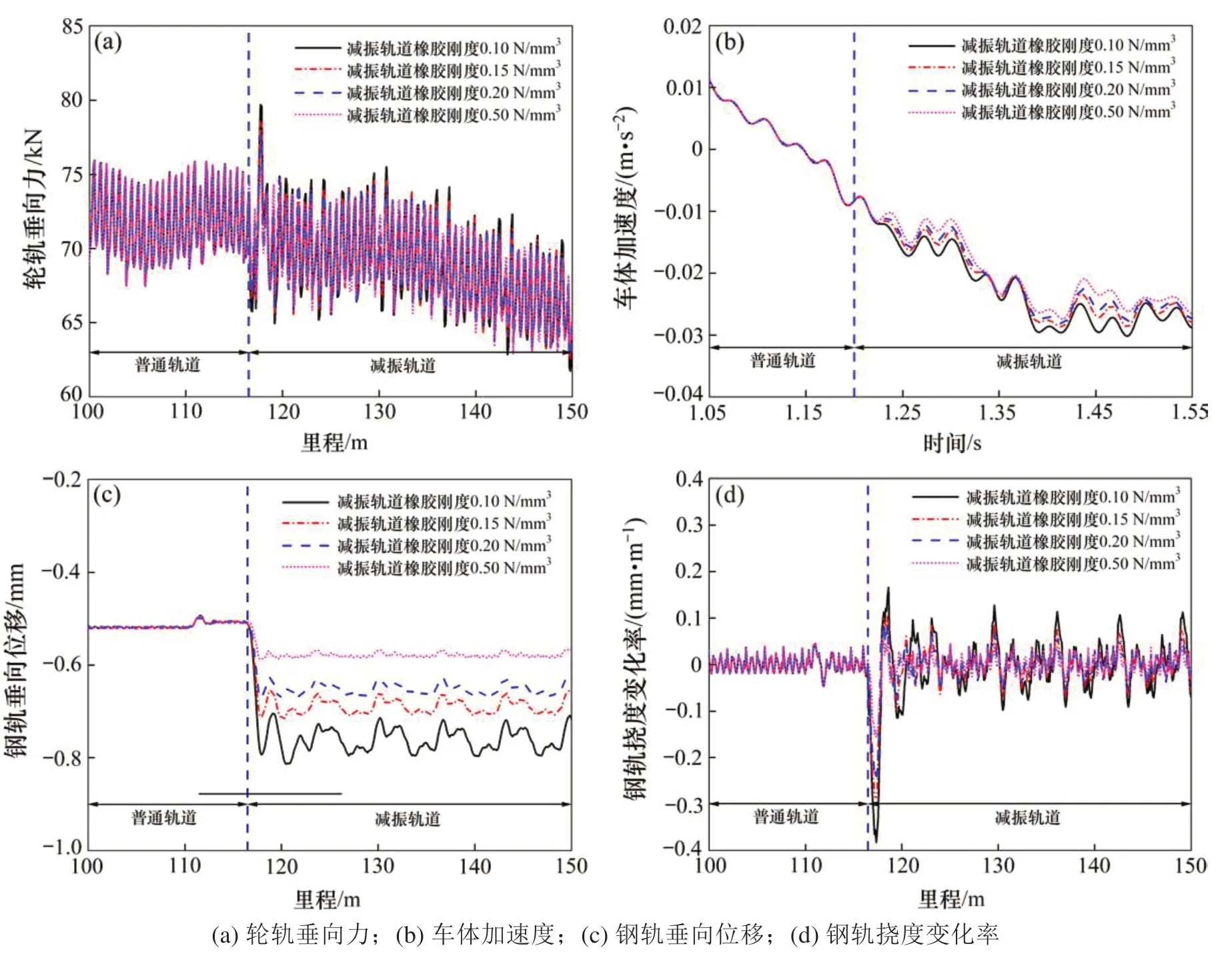
图6 过渡段刚度差对动力学评价指标的影响Fig.6 Influence of stiffness of rubber cushion on dynamic evaluation index

然而，从轨道结构的动力性能来看，当列车通过大跨桥普通轨道与减振轨道连接处时，钢轨垂向位移(钢轨挠度)和钢轨挠度变化率会在该连接处产生明显突变，且随着橡胶垫层刚度的增大呈负相关变化，即橡胶垫层刚度越小，钢轨垂向位移和钢轨挠度变化率突变值越大，具体如图6(c)和6(d)所示。其中，当橡胶垫层刚度分别取0.1，0.15，0.2和0.5 N/mm3时，钢轨挠度变化率峰值分别为−0.383，−0.291，−0.251，−0.156 mm/m。由此可以发现，当橡胶垫层刚度为0.1 N/mm3时，该连接处的钢轨挠度变化率峰值超过了相关的标准限值0.3 mm/m。在此情况下不利于保证行车的安全性和轨道结构的高平顺性。因此，为了保证高速铁路轨道结构的高平顺性，改善行车的安全性和平稳性，建议在轨下基础刚度突变处增设一定长度的过渡段，而过渡段的设置方式建议在减振轨道一定范围内通过增大橡胶垫层刚度的方式来增设，从而保证钢轨挠度变化率峰值控制在限值以内。

3.3.2 过渡段橡胶垫层刚度的合理布置和取值

由3.3.1节所得结论，即普通轨道与减振轨道连接处两侧的刚度差主要对钢轨挠度变化率的影响显著，对轮轨垂向力和车体加速度的影响较小。当减振轨道橡胶垫层刚度为0.1 N/mm3时，钢轨挠度变化率峰值超限，不利于保证行车的安全性和轨道结构的高平顺性。本节在研究过渡段橡胶刚度的合理取值范围时，选取了减振轨道橡胶垫层面刚度为0.1 N/mm3的过渡段工况，采用刚度分级的过渡方式，对过渡段的橡胶垫层刚度进行布置，并拟定2种过渡段橡胶垫层刚度布置方案，仅分析不同过渡段橡胶垫层刚度的布置方案对钢轨挠度变化率的影响，从而确定过渡段橡胶垫层刚度的合理布置方式和取值。其中，布置方案可分为1级刚度过渡和2级刚度过渡2种类型，靠近减振轨道为第1级，每级过渡2块轨道板，相邻两级过渡段刚度比取值为1.5。仿真计算后，不同刚度过渡方式下钢轨挠度变化率的变化情况如图7所示。

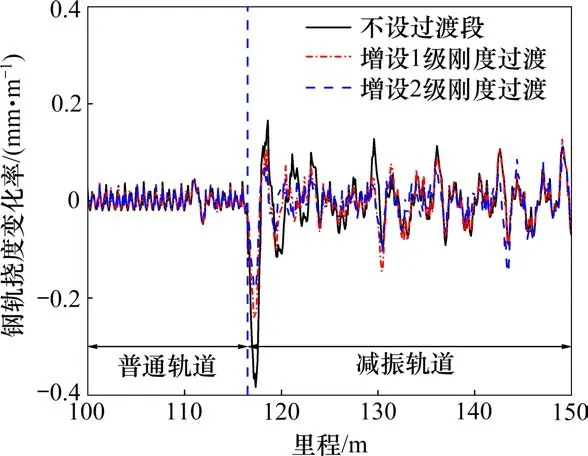
图7 不同刚度过渡方式下钢轨挠度变化率Fig.7 Change rate of rail deflection under different transition modes of stiffness

由图7可知，与不设过渡段相比，在连接处增设过渡段对钢轨挠度变化率的影响显著。其中，增设1级刚度过渡、增设2级刚度过渡的钢轨挠度变化率峰值分别为−0.239 mm/m和−0.179 mm/m，较不设过渡段的钢轨挠度变化率峰值，分别减少37.5%和53.3%。且增设2级刚度过渡的钢轨挠度变化率峰值较增设1级刚度过渡的钢轨挠度变化率峰值减少15.8%。此时，说明采用刚度分级的过渡方式不仅可以改善轨道刚度突变引起的钢轨挠度变化率超限问题，还能实现轨道刚度的逐渐过渡，保证每一级刚度差引起的钢轨挠度变化率也不超过其限值。同时，为了明确相邻两级过渡段刚度比取值对刚度分级的影响，本节还研究了在增设1级刚度过渡和增设2级刚度过渡2种情况下，相邻两级刚度比分别为1.1，1.3，1.5，1.7，2，2.2和2.5时钢轨挠度变化率峰值(取绝对值)的变化规律，具体见图8。

由图8可知，从总体上看，增设2级刚度过渡对改善钢轨挠度变化率峰值的效果更佳，且随着相邻两级过渡段刚度比值的增大，钢轨挠度变化率峰值基本上呈逐渐减小的趋势。其中，在增设2级刚度过渡情况下，当相邻两级刚度比小(大)于1.8时，钢轨挠度变化率峰值随着刚度比的增大呈负(正)相关变化；当相邻两级刚度比为1.8时，钢轨挠度变化率峰值最小，为−0.168 mm/m；然而，当相邻两级刚度比为1.1时，钢轨挠度变化率峰值接近其限值，因此建议相邻两级刚度比不宜小于1.1。

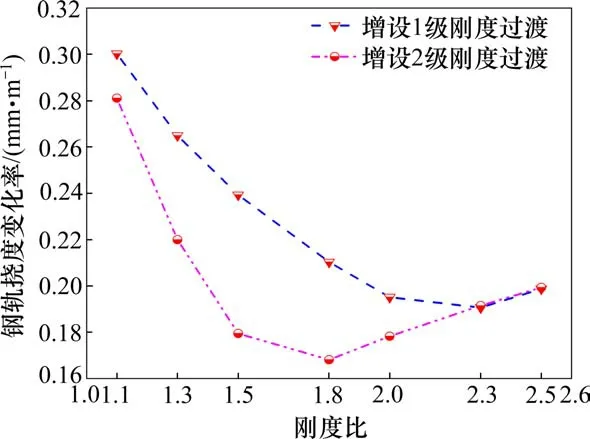
图8 不同刚度比下钢轨挠度变化率Fig.8 Change rate of rail deflection under different stiffness ratios

3.4 过渡段长度对过渡段动力特性的影响

为了明确大跨减振轨道过渡段长度的合理取值，本节选取5种不同的过渡段长度工况进行计算，其中，过渡段长度分别为12.8，19.2，25.6，32和38.4 m。过渡段橡胶垫层刚度采用刚度分级的过渡方式，每级过渡2块轨道板，相邻两级刚度比为1.5。仿真后的过渡段钢轨挠度变化率如图9所示。

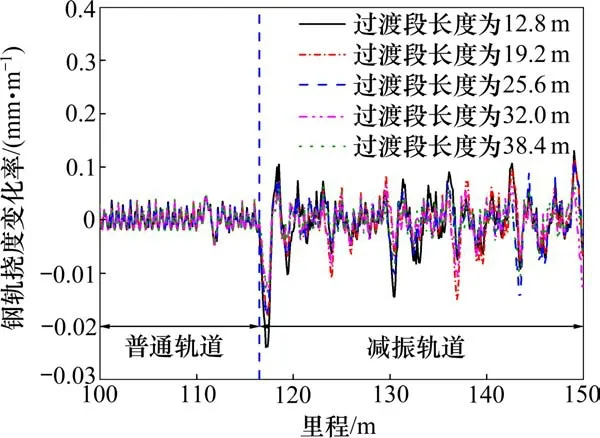
图9 不同过渡段长度下钢轨挠度变化率Fig.9 Change rate of rail deflection under different length of transition section

由图9可知，过渡段长度越长，钢轨挠度变化率峰值越小。其中，当过渡段长度分别为12.8，19.2，25.6，32和38.4 m时，其钢轨挠度变化率峰值分别为−0.239，−0.179，−0.178，−0.136和−0.131 mm/m，较不设过渡段的钢轨挠度变化率峰值分别降低37.5%，53.3%，53.5%，64.5%和65.8%。可见不同过渡段长度对钢轨挠度变化率的影响较大，且当过渡段长度大于20 m时，过渡段长度对钢轨挠度变化率更显著。然而，当过渡段长度大于30 m时，钢轨挠度变化率峰值受过渡段长度变化的影响并不明显。同时，从经济成本的角度出发，过渡段长度越长，施工成本越大。因此，综合考虑行车安全及施工成本等因素的影响，建议过渡段长度宜取20～30 m。

4 结论与建议

1)考虑大跨桥挠曲变形主要对钢轨挠度变化率的影响较为显著，对轮轨垂向力、车体加速度的影响较小。因此，在分析大跨桥上减振轨道过渡段橡胶垫层刚度、过渡段长度对其动力响应的影响时，必须考虑大跨桥挠曲变形的影响。

2)普通轨道与减振轨道连接处两侧的刚度差主要对钢轨挠度变化率的影响显著，对轮轨垂向力、车体加速度的影响较小。当橡胶垫层面刚度为0.1 N/mm3时，钢轨挠度变化率峰值超过0.3 mm/m限值，但在轨下基础刚度突变处增设过渡段可以控制钢轨挠度变化率在限值以内。过渡段建议采用刚度分级的过渡方式，每级过渡2块轨道板，相邻两级刚度比不宜小于1.1。

3)不同过渡段长度对钢轨挠度变化率的影响较大，且当过渡段长度大于20 m时，过渡段长度对钢轨挠度变化率的影响更显著，然而，当过渡段长度大于30 m时，钢轨挠度变化率峰值受过渡段长度变化的影响并不明显。且过渡段长度越长，施工成本越大。因此，综合考虑行车安全性以及施工成本等因素的影响，过渡段长度建议取20～30 m。