基于PSO−BP神经网络的隧道绿色建造污水处理预测模型

周中，张俊杰，丁昊晖，李繁

(中南大学 土木工程学院，湖南 长沙410075)

随着我国隧道建设的不断发展和完善，施工过程中对生态环境保护的要求也越来越严格，若处理不当，则会对周边的生态环境造成不可逆的损害。因此，践行绿色隧道施工理念尤为重要[1-3]，水污染防治作为绿色施工的重要一环也是势在必行[4]。在隧道施工期间往往会产生大量的污水，如果不经过处理直接排出，将会对周边的水源造成严重的污染，因此需要在隧道施工污水排放前进行无害化处理。隧道施工排放的污水往往存在浊度偏高的问题，目前对于该类污水主要采用絮凝沉淀法进行处理[5-6]，其中聚丙烯酰胺(PAM)由于相对于传统无机絮凝试剂具有用量小、絮凝效果好、絮凝时间短的特点被广泛用于此类污水处理过程中[7-8]。隧道施工污水处理是一个动态的过程，污水的浊度会受到施工快慢、降雨情况和混凝土组成成分等外界因素的影响而发生改变，这种动态变化也就要求在污水处理过程中要不断地对絮凝剂的投药量和污水的pH值等参数进行调整，尽可能提高隧道施工污水的处理效果，使得处理后的污水能够达到排放标准。采用传统的试验方法进行参数优化时往往需要耗费大量的时间和材料，难以应用在该类指标参数变化幅度较大的污水处理中。因此,寻找一种能够依据污水中浊度的变化情况快速对处理参数进行调整的方法对于隧道水污染防止有重要的意义。近年来，已有部分学者将神经网络运用到污水处理中各类污染物的预测过程，并根据预测结果对污水处理进行智能控制和优化。陈威等[9]考虑污水处理厂密切相关的7个因素建立BP神经网络对出水的氨氮含量进行预测，其实测值和预测值误差均在±2.5 mg/L范围内；杨壮等[10]将灰色理论与神经网络相结合，实现了对污水处理中的COD含量较高精度的预测；张晓航等[11]采用神经网络的方法对磁絮凝处理矿井水效果进行预测，依据预测结果对污水处理参数进行调整以达到投药量最小、电耗最低的情况下，出水浊度最小的目的。CONG等[12]为了提高条件变化频繁的污水处理过程水质评价的准确性，利用神经网络有效地估算了条件不断变化情况下的出水水质。上述研究表明，采用各类神经网络能够对污水处理中出现的各类污染物进行较为准确的预测，因此将神经网络应用到隧道污水处理后的浊度预测是一个很好的选择。然而传统的BP神经网络在训练过程中容易陷入局部最优解的问题，导致训练后的网络性能不理想[13-14]。为了解决该问题，本文采用粒子群算法对BP神经网络的初始阈值和权重进行优化，建立了PSO-BP隧道污水处理浊度预测模型，对隧道排放污水处理后的出水浊度进行预测，并基于该模型采用计算机编程语言设计了隧道施工污水处理预测系统，对现有的隧道施工污水处理工艺进行了优化，在实际工程应用中取得了较好的效果。

1 PSO-BP神经网络算法

1.1 BP神经网络算法

BP神经网络由输入层、隐含层和输出层构成[15-16]，结构如图1所示。学习过程主要分为正向传递信息与反向传播误差2个部分，通过多次循环训练不断调整神经网络的权值和阈值，使得输出结果趋近目标值，从而完成对网络的训练。

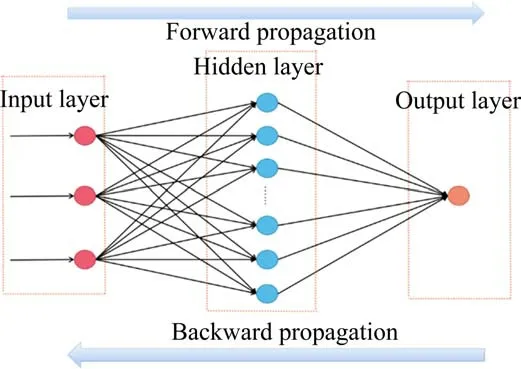
图1 BP神经网络结构图Fig.1 Structure diagram of BP neural network

1.2 基于粒子群优化的BP神经网络算法

粒子群优化算法[17-18]在初始阶段会随机生成一定数量的粒子群，每个粒子都是具有一定空间维度数的向量组。在BP神经网络初始权重和阈值的优化问题中，该向量组就代表着网络权重和阈值的一个潜在最优解，向量组的空间维度则由神经网络结构中待优化的阈值和权重的总数量所决定。粒子群会对优化过程中的个体最优解，以及全局最优解进行记忆保存，并通过式(1)～(2)来对自身的速度以及位置参数进行更新，从而寻找优化问题的最优解。

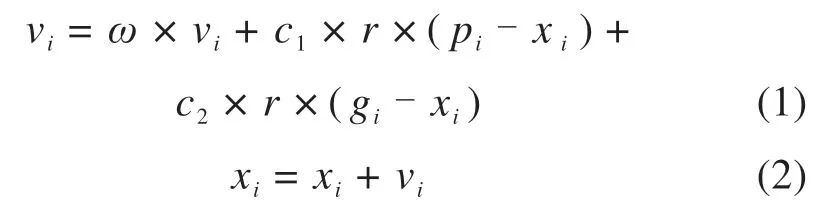
式(1)～(2)中：i=1,2,3,…,N，N为粒子群的总数;vi为粒子的速度；ωi为惯性因子；c1和c2为学习因子；pi为个体最优解；gi为全体最优解；r为0-1之间的随机常数；xi而为粒子所处的位置。

基于上述优化步骤构建的PSO-BP神经网络算法的流程图如图2所示，其中适应性函数的构造是该算法实现对BP神经网络优化的重要步骤，本文采用的适应性函数如下：

图2 PSO-BP神经网络建立流程图Fig.2 Flow chart of PSO-BP neural network establishment

式中：S为样本的个数；N为粒子群所处空间的维度；yki为神经网络的预测输出值；y'ki为神经网络的期望输出值。

2 预测模型参数确定与优化

2.1 BP神经网络结构的确定

选取隧道排放污水未处理前的浊度、絮凝剂的分子量和投药量、pH值、搅拌时间和搅拌速度在内的6个会对污水浊度处理效果产生影响的参数作为神经网络的输入值，污水经过处理后的出水浊度作为神经网络的输出值，则网络的输入单元个数m为6，输出单元个数n为1，隐藏层单元个数则根据式(4)进行选取，本文选择隐藏层单元数为8。

式中：l为隐藏层的单元个数；a为[1,10]之间的整数。

由于训练样本数量有限，为了防止在训练的过程中出现过拟合的现象，将隐藏层的层数设置为1。

2.2 数据预处理

样本数据中不同参数变量的量纲和量纲单位往往不同，经常会出现数据的值不在同一量级上的情况，这会导致神经网络在训练过程中遇到难以收敛或者梯度爆炸等问题，因此需要对原始数据进行归一化处理[19]，本文采用的处理方式如下。

式中：x'为归一化处理后的数据；x为原始数据；μ为样本某一参数数据的均值；σ为样本某一参数数据的标准差。

2.3 PSO算法参数选取

根据已经确定的BP神经网络的结构可以通过式(5)计算出粒子群所处的空间维度N=1+8+8×6+8×1=65。

因此粒子i在该空间的速度向量可以表示为vi=(v1,v2,v3,…,v65)，位置向量可以表示为xi=(x1,x2,x3,…,x65)。学习因子c1和c2均设置为2。

惯性权重对于PSO算法的优化性能影响非常显著，采用固定的值往往不能得到很好的搜索效果，因此本文采用典型线性递减策略[20]来确定w，计算公式如下。

式中：wmax为惯性权重最大值，取值为0.9；wmin为惯性权重最小值，取值为0.4；t为当前迭代次数；tmax为总共迭代次数。

为了设置合理的粒子群规模和迭代次数，采用不同数量的粒子群进行神经网络初始参数的对比优化试验，得到了各粒子群规模适应度收敛时的迭代次数区间以及收敛后的适应度大小，结果如表1所示。其中，收敛时的迭代次数采用区间的形式是因为即使收敛后适应度也会出现小范围的波动，因此无法精确到某一个迭代次数，采用区间的表示方法更加合理准确。

表1 不同规模粒子群迭代试验结果Table 1 Iterative test results of particle swarm optimization with different scales

从表1中结果可以看出，当粒子群规模为200时，收敛后的适应度值最小，表明在该粒子群规模下对于BP神经网络的初始权值和阈值的优化效果最好。此外，不同的粒子群规模下适应度达到收敛时的迭代次数范围均落在了[300,500]的区间中。基于上述结果，为了在保证对神经网络充分优化的同时，减小迭代次数，以提升运算的效率，设置粒子群规模为200，迭代次数为500。

2.4 模型的评估指标

采用均方差(MSE)以及样本的拟合度(R2)作为本文建立的PSO-BP预测模型的评估指标，MSE和R2的计算公式分别为：其中：N为样本个数；Yi为隧道污水的出水浊度预测值；Y'i为隧道污水的出水浊度实际值；Yˉ为隧道污水的实际出水浊度平均值。

3 模型验证

分析依托于桂柳高速公路隧道，测定该隧道施工排放污水水质指标：浊度为126.2～1 489.1 NTU；COD为1～30 mg/L；NH3-N为0.5～30 mg/L；pH值为7～9。

试验水样配置参考隧道施工现场污水水质，污水处理选用的絮凝药剂为阴离子聚丙烯酰胺，采用WGZ-800浊度仪测定污水浊度。通过改变模拟污水的原水浊度、聚丙烯酰胺的分子量和投药量、pH值、搅拌时间和搅拌速度等6个可能对隧道施工污水絮凝处理后的出水浊度产生影响的因素共获取了共133组试验数据，试验过程如图3所示，部分试验数据如表2所示。利用试验数据集对2种网络进行训练，所得评估指标结果如图4～6所示。值得说明的是，为了验证本文PSO-BP能够有效解决传统BP神经网络在训练过程中容易陷入局部最优的问题，在获取MSE评估指标的过程中，除了单独对2种网络模型进行训练，还增加了一组对照训练试验。该试验首先对BP神经网络进行训练至其收敛，并保存此时的网络权重和阈值参数，将其赋值给PSO算法中的其中一个初始粒子，该初始粒子和粒子群共同进行神经网络参数的优化，并对优化后的神经网络模型再次进行训练至收敛，对比优化前后的MSE值的变化情况从而判断PSO优化算法是否能够帮助神经网络模型在训练过程中跳出局部最优解。

表2 隧道施工模拟污水处理原始数据举例Table 2 Example of original data of simulated sewage treatment in tunnel construction

图3 模拟隧道施工污水处理试验Fig.3 Sewage treatment test of simulated tunnel construction

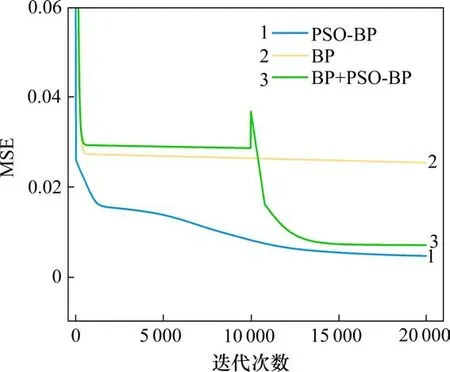
图4 神经网络MSE对比图Fig.4 Neural network MSE comparison chart

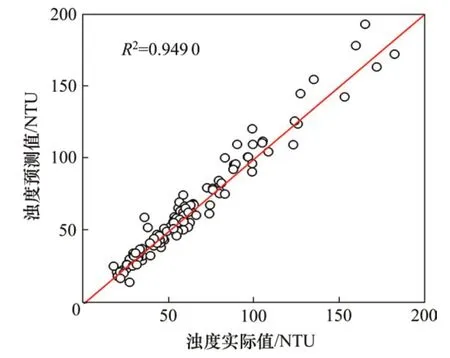
图5 PSO-BP训练样本整体拟合情况Fig.5 Overall fitting of PSO-BP training samples

图6 BP训练样本整体拟合情况Fig.6 Overall fitting of BP training samples

由图4～6可以看出，相较于传统BP神经网络，PSO-BP神经网络训练过程中的MSE更小，且R2更高，这表明在进行数据训练的过程中，PSOBP神经网络的预测值更加趋近于训练样本的实际值，模型的预测能力得到了更好的训练。此外，分析图4中对照组训练过程的MSE变化曲线可知，BP神经网络训练收敛后得到的权重和阈值经过PSO算法优化后再次进行训练，MSE将进一步收敛至另一个更小的最优解，表明PSO优化算法能够帮助传统的BP神经网络在训练过程中跳出局部最优，从而进一步减小训练的误差。

在神经网络的训练过程中经常会出现训练样本的预测误差很小，但是实际测试时误差明显增加的情况。因此，为了检验模型训练后的实际预测效果以及泛化能力，对现场隧道污水实际处理后的污水取样检测，将模型预测的浊度结果与现场污水处理后实际浊度结果进行对比测试，并与BP神经网络预测结果进行比较，分析结果如图7和图8以及表3所示。

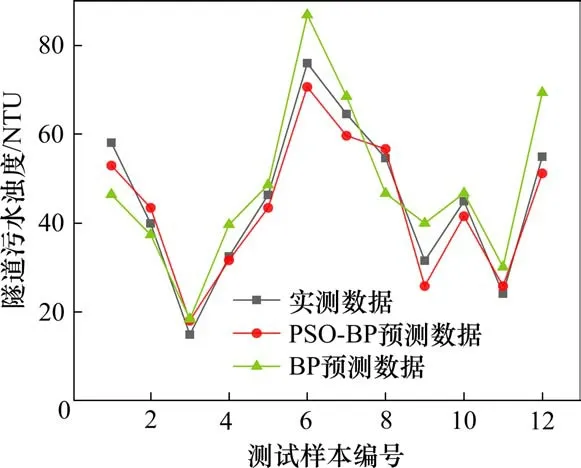
图7 2种神经网络预测值与实际值对比图Fig.7 Comparison of predicted value and experimental value of two kinds of neural networks

由表3结果可知，PSO-BP神经网络测试的平均绝对误差为3.532 NTU，平均相对误差为8.86%，2项指标参数均小于BP神经网络，并且有83.33%的测试样本预测相对误差少于10%。由图7和图8可知，PSO-BP神经网络的预测值与实际值的拟合程度要高于BP神经网络，且整体的相对误差要更小。综上分析可知，采用本文提出的PSO-BP神经网络模型能够有效地对隧道施工污水絮凝处理过程后的出水浊度进行预测，并且相对于传统的BP神经网络具有更好的预测精度以及泛化能力。

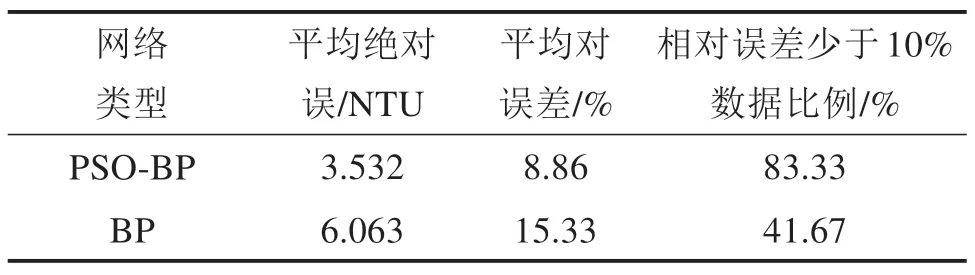
表3 2种神经网络测试结果比较Table 3 Comparison of test results of two neural networks

图8 2种神经相对误差对比图Fig.8 Comparison of relative errors of two kinds of neural networks

4 工程应用

桂柳高速公路隧道施工污水仅仅通过3级沉淀池的自然沉淀作用后就被排至地表河流，由于场地的限制，沉淀池较小，污水中的悬浮物在流动过程中无法充分沉淀去除，这也就导致污水经过原有隧道污水工艺处理的效果并不理想，排放的污水存在浊度偏高的问题。为将PSO-BP污水处理浊度预测模型应用于桂柳高速公路隧道施工污水处理工艺的优化中，采用计算机编程语言设计了隧道施工污水处理效果预测系统如图9～10所示，该系统输入污水的原水浊度、投药量、聚丙烯酰胺的分子量、搅拌速度、pH值和搅拌时间等6项参数后点击计算按钮，即可调用已经训练完成的PSO-BP神经网络进行运算，得出相应参数下的隧道污水经处理后的出水浊度预测值。且该系统还具有网络更新功能，使用者可以向图10中的表格添加新的污水处理数据或者导入外部表格文件对神经网络进行更新，从而不断提高该网络的预测准确性。

图9 软件主界面Fig.9 Software main interface

图10 神经网络更新界面Fig.10 Neural network update interface

利用该系统对现场隧道施工污水处理工艺进行优化，污水排放至沉淀池后首先采用在线浊度仪对隧道施工污水的浊度进行实时监测，将获取的浊度数据输入隧道施工污水处理预测系统，利用该系统确定处理过程中聚丙烯酰胺的投药量和分子量以及盐酸用量等参数并进行相应调整，之后再投放至混凝池进行絮凝处理，处理后的污水经过新一轮的浊度监测若达到排放标准后将会被排出，优化后的隧道施工污水处理工艺如图11所示。采用该工艺排放污水的浊度得到了明显降低，有效解决了桂柳高速公路隧道施工污水处理过程中参数难以动态调整、浊度去除效果不佳的问题，对维护周边自然生态具有重要意义，且能够对绿色施工过程中的水污染防治具有一定的参考价值。

图11 结合PSO-BP神经网络模型的隧道施工污水处理工艺Fig.11 Tunnel construction sewage treatment process based on PSO-BP neural network model

5 结论

1)提出了基于粒子群优化算法的PSO-BP隧道污水处理预测模型，并采用该模型对隧道施工污水处理后的出水浊度进行了对比预测，研究结果表明：采用PSO算法对BP初始权重和阈值进行优化，有效提高了神经网络模型的预测精度，并解决了传统BP神经网络容易陷入局部最优的问题。

2)基于提出的PSO-BP网络模型设计了隧道施工污水处理效果预测系统，并采用该系统对现场隧道施工污水处理工艺进行优化，使得在实际隧道排放污水处理过程中能够灵活调整各项工艺参数，以保证排放的污水浊度尽可能地低，达到绿色施工的目的。