高速磁浮整体式预应力轨道梁温度场与变形分析

文泉，王春江，孙向东，常邑

(1.上海交通大学 船舶海洋与建筑工程学院，上海200240；2.中车青岛四方机车车辆股份有限公司，山东 青岛266111)

我国青岛高速磁浮试验线(青岛线)轨道梁采用整体式预应力混凝土梁，功能件和轨道梁一体浇筑，具有截面刚度大、整体性好等优点，在磁浮线路中有较好的应用前景。运营环境中的磁浮轨道梁结构，其温度场受季节和日照温度变化影响很大，具有不均匀性、周期性和时变性等特点。相关学者对日照温度荷载下磁浮轨道梁结构温度分布和温度变形做了诸多研究。MANGERIG等[1-2]对Emsland试验线轨道梁温度效应进行了计算并提出了结构优化方案。KIM[3]建立了模块化轨道钢梁三维模型，研究了多种热环境下轨道梁温度效应；ZHANG等[4-5]研究了轨道梁温度变形对车桥耦合响应的影响；祁炎萍[6]对北京磁浮交通S1线承轨梁建立了有限元模型并对承轨梁在温度和其他作用组合下的受力行为进行了研究；李国强等[7]对上海线磁浮钢梁日照温度场及温度变形做了实测及数值研究；戴公连等[8]对长沙磁浮运营线进行了现场监测，给出了温度场时变规律；莫然等[9]对青岛线轨道梁连接构件对温度场的影响做了研究。可以看出，国内外关于日照温度荷载下磁浮轨道梁的研究重点多数集中在二维温度场分布及一维梁单元温度效应研究，对磁浮列车荷载和环境双重因素影响下考虑预应力的三维轨道梁的变形的空间、时间上的变化规律鲜有报道。本文基于三维条件下分析磁浮轨道梁在磁浮列车、温度载荷和预应力共同作用下的结构性能。

1 计算模型

以我国青岛线整体式预应力混凝土轨道梁为计算对象，一跨轨道梁由4块轨道板和1段承重梁组成。一跨轨道梁长度24.768 m。每块轨道板长度6.182 m，截面宽度为2.8 m，高度为0.35 m；承重梁截面宽度为3.0 m，高度为2.4 m。施工过程中轨道板精确定位后，与承重梁预留钢筋焊接连接，并采用自密实混凝土浇筑成一体。承重梁预应力采用后张法张拉施工，共有8根直径为15.2 mm的预应力筋。轨道梁采用混凝土标号为C60，预应力钢绞线标准强度fpk=1 860 MPa，预应力张拉控制应力为0.7fpk，预应力筋采用纵向抛物线形式布置，整体式预应力混凝土梁模型如图1所示。

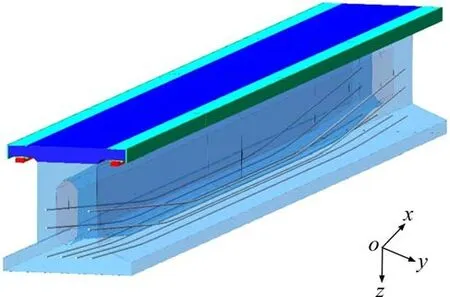
图1 整体式预应力混凝土轨道梁Fig.1 Prestressed overall concrete guideway beam

本文基于ABAQUS建立磁浮轨道梁日照温度场三维瞬态有限元分析模型。用隐式计算方法，时间步长取为60 s，进行72 h的瞬态传热分析，初始温度取大气平均温度，传热分析采用DC3D8单元，顺序热力耦合分析采用三维单元C3D8R，C60混凝土拉压弹性模量E=36 500 MPa，泊松比采用0.2。网格最小尺寸为0.02 m，最大尺寸为0.1 m，计算模型如图1所示。根据我国混凝土结构设计规范(GB50010—2010)和民用建筑热工设计规范(GB50176—2016)，混凝土热膨胀系数α=1.0×10-5，导热系数λ=10.6 kJ/(m∙h∙℃)，比热容c=0.96 kJ/(kg∙℃)；钢绞线热膨胀系数α=1.2×10-5，导热系数λ=209.5 kJ/(m∙h∙℃)，比热容c=0.48 kJ/(kg∙℃)。

本文采用节点耦合法[10]建立轨道梁中8根后张法预应力钢筋。通过引入虚拟预应力钢筋，并在虚拟预应力筋和真实预应力筋之间建立多个局部坐标系，在相对应节点之间通过刚性弹簧连接，虚拟预应力筋与混凝土之间采用ABAQUS“Embed”方式连接。采用降温法施加预应力，即在相应荷载步修正初始预应力钢筋温度的方式施加预应力。钢筋与混凝土之间的变形协调需经过多次修正，最终得到预应力施加效果。

2 轨道梁温度场分析

2.1 日照辐射温度场分析基本原理

在实时变化的日照环境下，钢筋混凝土结构不会有稳态传热的情况发生，日照温度效应只能采用瞬态传热分析来研究。温度值与空间坐标和时间坐标的变化都有关系，即T=f(x,y,z,t)。内部无热源(ϕ=0)情况下，三维瞬态热传导微分方程为：

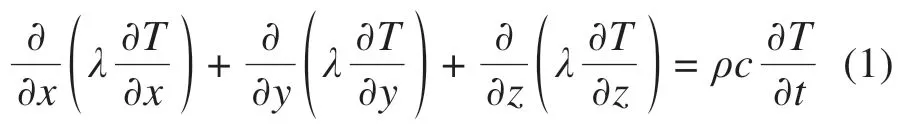
式中：λ,ρ,c,t分别表示物体的导热系数，W/(m∙℃)；密度，kg/m3；比热容，J/(kg∙℃)和h。

轨道梁与外界的热交换可以归纳为3种类型：太阳辐射、辐射换热和对流换热，q=qs+qr+qc。

太阳辐射的能量主要集中在可见光波段范围内。太阳总辐射qs按下式表示为第3类边界条件的形式：

式中：α为表面辐射热吸收系数(0<α<1)；I为垂直于表面的太阳辐射强度(W/m2)，I=Id+Ii+Ir，其中：Id为直接辐射强度；Ii为散射辐射强度；Ir为反射辐射强度。

辐射换热即为轨道梁通过其表面以电磁波形式向外界发出热辐射，同时又不断地吸收地表、大气及周围物体发出的热辐射，这种辐射与吸收的综合结果可按Stefan-Boltzmann定律表示：

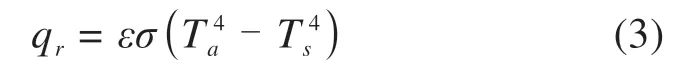
式中：Ta为大气温度，℃；Ts为表面温度，℃；ε为表面黑度系数，混凝土通常取0.88；σ为Stefan-Boltzmann常数，σ=5.677×10-8W/(m2∙℃4)。

对流换热是由于流体的宏观运动，各部分之间发生相对位移、冷热流体相互掺混所引起的热量传递过程。对流换热热流能量可由Newton冷却公式表示为：

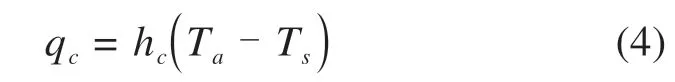
式中：hc为对流换热系数，W/(m2∙℃)，主要取决于风速、周围空气温度和表面粗糙度等。

2.2 日气温、风速变化影响

在一年当中，日气温变化规律较为一致。可以根据历年实测的日气温数据，给出日气温的变化规律，再进行曲线拟合得出用于计算每日任意时刻气温的数学模型。通常，箱体外部温度可取为介于日最高气温Tamax和日最低气温Tamin之间的正弦曲线[11]。

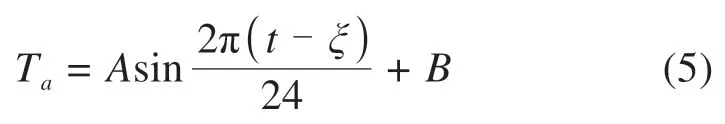
式中：t为时刻(0≤t<24)；A=(Tamax-Tamin)/2；B=(Tamax+Tamin)/2；ξ为最高气温滞后时刻，以早上6:00为参照时刻，如果最高气温出现在14:00，ξ=8；如果最高气温出现在15:00，ξ=9。

根据国家气象科学数据中心(data.cma.cn)气象资料，青岛地区夏季8月份累年日平均气温比其他月份要高，日序数为第218 d(8月7日)的累年日平均气温为全年最高，其数值为25.9℃，8月份累年平均日最高气温为28.8℃，8月份累年平均日最低气温为21.5℃。最高气温一般出现在14:00点左右。青岛地区近3年8月份相对晴朗连续1周逐时日气温数据与本文拟合气温曲线对比，如图2所示。气温拟合曲线与实际气温变化拟合度较好，可以在计算中采用。

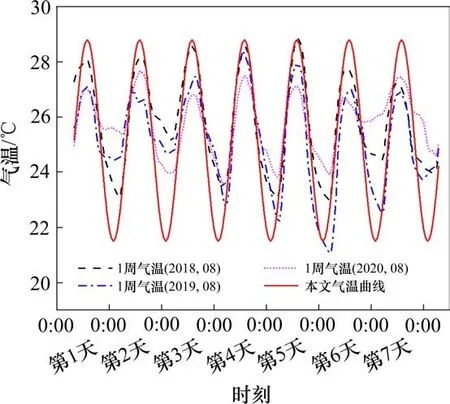
图2 实际/拟合日气温对比Fig.2 Comparison chart of actual/fitted daily temperature

对于箱梁内部空气，其温度在一天内波动较小，当缺乏实测数据时一般取为常值[12]：Tia=Tˉa+1.5℃，其中，Tˉa为日气温平均值。

由于当地风速随机性较大，本文取风速年平均值4.0 m/s。各截面对流换热系数hc(W/(m2∙℃))取值通常简化为关于风速的线性关系式[13]，轨道板上表面hc=19.99，侧面及下表面hc=17.99；承重梁下表面hc=17.49，侧面hc=18.99，内表面hc=3.5。

2.3 太阳辐射量计算

根据凯尔别克[14]的太阳瞬时辐射强度计算模型，通过经验式(6)和式(7)可以分别计算到达地面的和不同角度入射面的太阳直接辐射强度Id，

任意斜面上的散射强度可按式(8)计算：

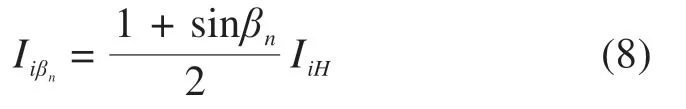
其中，IiH=(0.27I0-0.294Id)sinβs，式中：βn为表面外法线与地面之间的夹角；IiH为水平面上散射辐射强度；βs为太阳高度角。

任意斜面上地表短波反射Irβn可按式(9)计算：

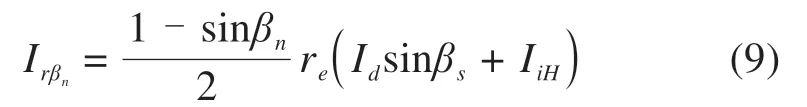
式中：re为地面反射率，re=0.2。

所以，轨道梁任意表面上太阳辐射总量为：

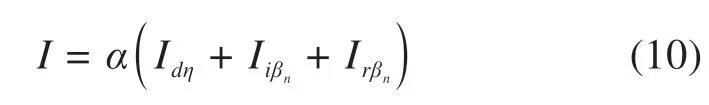
式中：α为表面辐射热吸收系数。

太阳辐射量也可采用直接测量的方式获得。本文使用Python语言编写了全时域任意截面太阳辐射计算程序。将程序计算得出青岛地区8月份相对晴朗连续1周到达地面上逐时太阳辐射总量与国家气象科学数据中心记录的太阳辐射总量数据做了对比。对比结果表示，本文太阳瞬时辐射强度计算模型与实际太阳辐射强度数据拟合较好。最后，给出了南北走向轨道梁各表面逐时太阳辐射总量，如图3所示。由图3可知，混凝土各表面太阳辐射总量较到达地面太阳辐射总量要小(计算中混凝土表面辐射热吸收系数取为0.65[15])；上表面太阳辐射热最大，下表面太阳辐射热最小，东西腹板上辐射强度出现明显的上下午周期性变化。

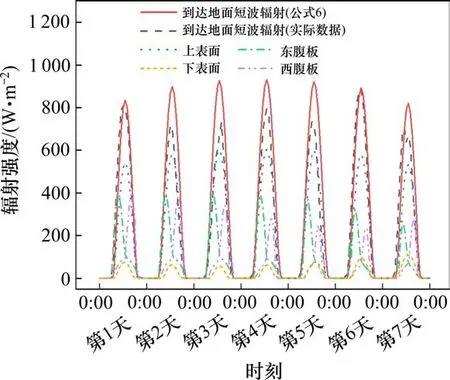
图3 各表面太阳辐射强度Fig.3 Solar radiation intensity over the surfaces

2.4 悬臂阴影计算

由于上翼缘相对两侧腹板存在外伸的情况，因此需考虑上翼缘外伸对腹板遮蔽效应的影响。根据解析几何推导得出阴影长度lsh计算公式(11)，各时刻受上翼缘遮蔽的区域无法接受太阳直射辐射，仅受到太阳散射和反射强度作用，如图4所示。

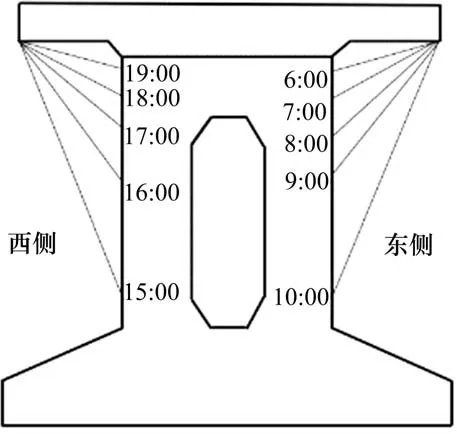
图4 时变腹板遮蔽长度Fig.4 Length of shadow over time

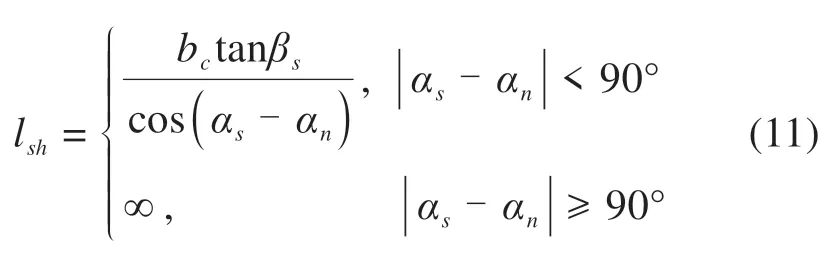
式中：bc为悬臂翼缘长度；αs和αn分别为太阳方位角和截面法线方位角。

3 ABAQUS温度场计算结果

3.1 轨道梁温度时程

为探究轨道梁温度时程规律，选取了轨道梁支座位置、变截面区域中间位置和跨中位置等3个截面，如图5所示。其中N1，N4和N7为轨道板上表面上的测点；N2，N5和N8为距轨道板上表面0.2 m的测点，N9，N10和N12为距腹板外侧0.15 m的测点；N3，N6和N11为腹板内表面上测点；N11为距承重梁顶部0.5 m的测点，各测点的温度-时间曲线如图6所示。

图5 测点位置示意图Fig.5 Location of the analyzed nodes

为探究轨道梁内部传热规律给出了如图6(a)所示9个测点的温度-时程曲线，可以看出：1)各测点温度同外界气温一样呈周期变化；2)各测点第2天与第3天的温度时程变化基本一致，可见轨道梁初始温度的取值仅对计算开始几个小时时长范围内的温度变化有影响。3)N1，N4和N7测点温度出现峰值时刻基本同外界气温；N2，N5和N8测点温度峰值出现时刻比外界气温滞后4 h。

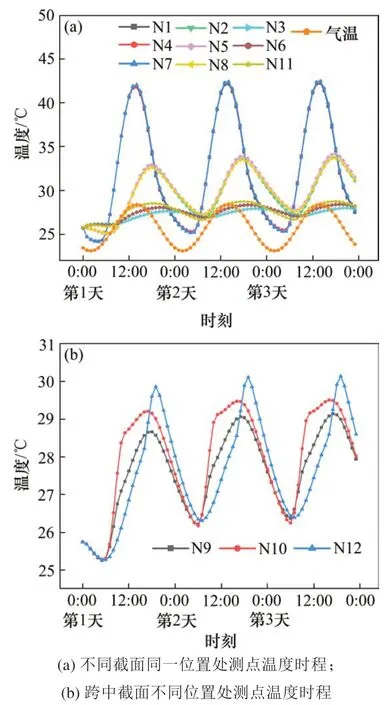
图6 各测点温度时程Fig.6 Temperature-time curves of analyzed nodes

为探究轨道梁温度场随日照辐射大小变化规律，给出了如图6(b)所示3个测点的温度-时程曲线，可以看出：1)N10和N12测点温度时程曲线呈现出关于12:00时刻对称形式，这是由于2个测点分别在上午和下午受到太阳照射的原因。2)N9和N10测点在10:00～12:00出现最大1℃左右温差，这是由于考虑了翼板对腹板遮蔽效应的结果。

3.2 纵向温度分布

根据图6(a)可知，N1，N4和N7测点温度变化一致，N2，N5和N8测点温度变化一致，可以表明：截面沿轴向无变化的直线梁可以取其任一截面进行二维温度场计算；N3，N6和N11测点表明变截面梁随着腹板厚度越厚，轨道梁体内表面温度越低，截面上温度梯度越大，所以在进行轨道梁设计计算时需注意变截面位置温度场分布。

3.3 竖向温度分布

为探究轨道梁温度场竖向分布规律，给出了支点、跨中和变截面，东西两侧腹板中线处竖向温度分布变化曲线如图7所示。根据时程分析结果，最大竖向温差发生在14:00。西面支点腹板中线从顶面向下0.5 m范围内发生了15℃左右温度梯度降低，随后跨中、支点和变截面处腹板保持27℃左右温度不变，可以看出，14:00时刻东侧腹板温度普遍高于西侧腹板，这是由于东侧腹板经过一上午太阳直接辐射而西侧腹板下午才开始受太阳直接辐射所导致。腹板越厚，腹板中线温度越低，符合混凝土传热规律。东侧腹板底部出现约4℃左右的提升，这是由于梁底面反射辐射和西侧腹板下翼缘横向传热共同导致的现象。

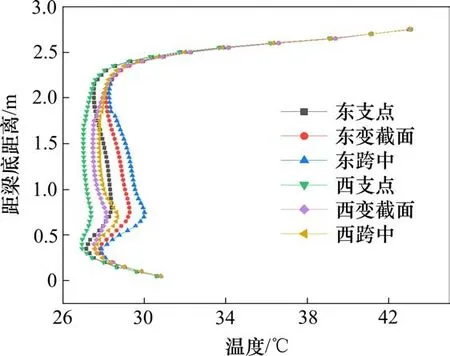
图7 东、西侧腹板竖向温度梯度分布Fig.7 Vertical temperature gradient of webs

3.4 横向温度分布

根据相关文献调查以及东西侧温度时程变化的对称性，最大横向温度梯度通常会出现在日出后几个小时和日落前几个小时，所以本文给出了梁跨中距离梁底0.3 m处各位置上下午时刻横向温度分布时程曲线，如图8所示。最大横向温差发生在11:00和15:00，最大横向温差在15℃左右。上午11:00时刻，由于整个轨道梁外部气温升温阶段，所以东西两侧腹板横向温度由外向内减小，且东侧腹板温度高于西侧腹板温度。下午15:00时刻，太阳直接辐射在西侧腹板，所以西侧腹板温度高于东侧腹板温度，且由于下午气温开始下降，东侧腹板外侧局部开始降温。

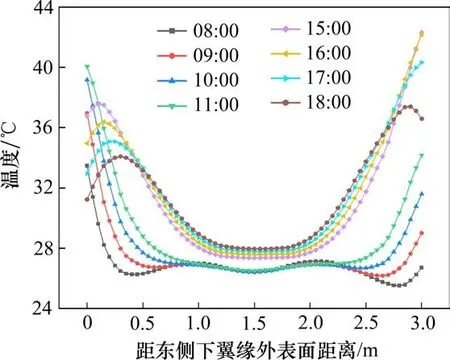
图8 各时刻横向温度梯度Fig.8 Lateral temperature gradient over time

3.5 我国规范对温度梯度的规定

根据我国现有的《高速磁浮交通设计规范》(征求意见稿)6.3.26规定：磁浮轨道梁的温度梯度选取宜参照《铁路钢筋混凝土和预应力混凝土结构设计规范》(TB10002.3—2005)的温差梯度模式。规范中规定，对于无砟无枕轨道箱梁温差的计算，应分别考虑沿梁高方向的温差荷载和2个方向的组合温差荷载。

根据规范，磁浮轨道梁截面竖向和横向温差梯度分别为Ty=20e-5y，Tx=16e-7x。根据3.3和3.4节中分析，磁浮轨道梁的温差分布模式与规范不完全符合，主要表现在不是向一侧单调减少。所以本文综合数值模拟结果、文献及国内外相关规范建议，给出了分段拟合曲线。规范与本文竖向、横向温差梯度模式对比分别如图9和图10所示。

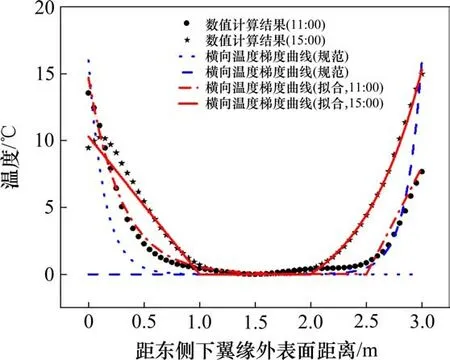
图10 横向温度梯度拟合曲线Fig.10 Fitting curves of lateral temperature gradient

竖向温差梯度拟合为2段：1)梁底0.3 m以上温差梯度采用指数温度模式：Ty=17.7e-4.9y，y为距轨道板上表面距离，m；2)梁底0.3 m范围内存在4℃负温差采用直线拟合。由图9可以看出，规范竖向温差梯度模式与本文竖向温差梯度拟合曲线在上部分指数衰减速率较为一致，前者初始温差略大于后者，说明规范竖向温差梯度模式包络性较好。二者不同点在于规范温差梯度模式为向单侧减少，而拟合曲线下部范围内存在负温差，更加符合实际。

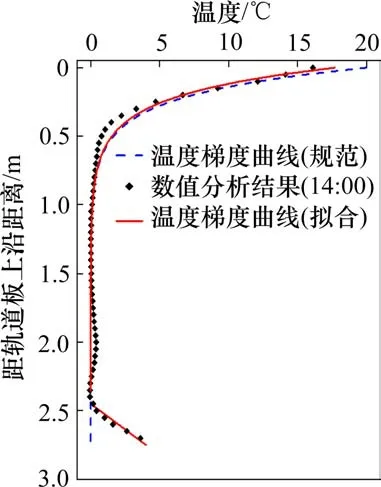
图9 竖向温度梯度拟合曲线Fig.9 Fitting curves of vertical temperature gradient

给出上午11:00和下午15:00横向温差梯度拟合曲线，见图10。考虑到拟合效果和与竖向温差梯度的公式一致性，上午11:00时刻横向温度梯度拟合为3段：1)距东侧翼缘外侧1.0 m以内拟合为指数温度模式：Tx=14.7⋅e-3.3x。2)距西侧翼缘外侧0.5 m以内采用直线拟合，线性温差为7.7℃。3)中间1.5 m范围内温差为0。下午15:00时刻，考虑到此时东侧表面局部降温不足1℃，忽略其局部降温并将此时的横向温差分布拟合为3段：1)距东侧翼缘外侧1.0 m采用直线拟合，线性温差为10.3℃。2)距西侧翼缘外侧1.5 m以内拟合为指数温度模式：Tx'=18.3⋅e-1.8x′，式中x'为距西侧外表面距离，m。3)中间1.0 m范围内温差为0。由图10可以看出，规范横向温差梯度模式与本文11:00和15:00时刻横向温差梯度拟合曲线初始温差较为一致，前者指数衰减速率大于后者，说明横向温差梯度模式包络性较好。二者不同点在于规范温差梯度模式为向单侧减少，而拟合曲线下部范围内存在负温差，更加符合实际。

4 轨道梁热力耦合变形分析

4.1 热力耦合分析基本原理

热力耦合分析根据是否考虑应力场与温度场的相互影响分为顺序热力耦合和完全热力耦合分析2种模式。顺序热力耦合计算中，首先分离温度场，忽略平衡方程中的应力和变形对温度分布的影响，独立解决温度场问题，得到温度场后再将温度场作为输入，求得轨道梁热应力。适用于温度场和应力场耦合不是非常强烈的情况。磁浮轨道梁本身的热能与变形对环境的影响可以忽略不计，故可采用顺序热力耦合分析。

4.2 热力耦合变形分析

基于本文计算得出的轨道梁温度场，对轨道梁进行在恒载、磁浮列车荷载和日照温度荷载下的顺序热-力耦合分析。本文计算过程中考虑由温度变化对钢绞线预应力水平的影响，并给出了单跨简支轨道梁在恒载、车辆、温度和2种预应力水平下的热力耦合，共5种工况下各最大变形量以及关键位置最大应力见表1和表2。为更加明确给出各荷载下的轨道梁变形情况，车辆和温度工况计算时未计入轨道梁自重。根据《高速磁浮交通设计规范》(征求意见稿)中对变形限值的定义，对单跨简支轨道梁，车辆荷载(按竖向静活载Pz=26.8 kN/m，Py=4.1 kN/m加载)引起的最大挠度值应小于L/4 000，横向位移值应小于L/15 000，梁端转角不应大于0.000 8 rad。由温差引起的最大挠度值应小于L/6 500，横向位移值应小于L/5 800。

根据表1和表2可知，1)轨道梁在车辆工况(计轨道梁自重)时最大竖向挠度为4.333 mm<6.192 mm；最大横向位移为0.472 mm<1.650 mm；最大梁端转角为0.000 519 rad<0.000 8 rad。2)轨道梁在温度工况下(计轨道梁自重)最大竖向挠度为2.088 mm<3.810 mm；最大横向位移为1.093 mm<1.650 mm；最大梁端转角为0.000 286 rad<0.000 8 rad。轨道板混凝土最大主拉应力3.271 MPa<3.5 MPa；最大主压应力27.511 MPa<40.0 MPa，钢绞线最大拉应力1 359.251 MPa<1 860.0 MPa。轨道梁在各工况下的应力及变形均满足规范强度、刚度限值要求，轨道梁受力性能良好。

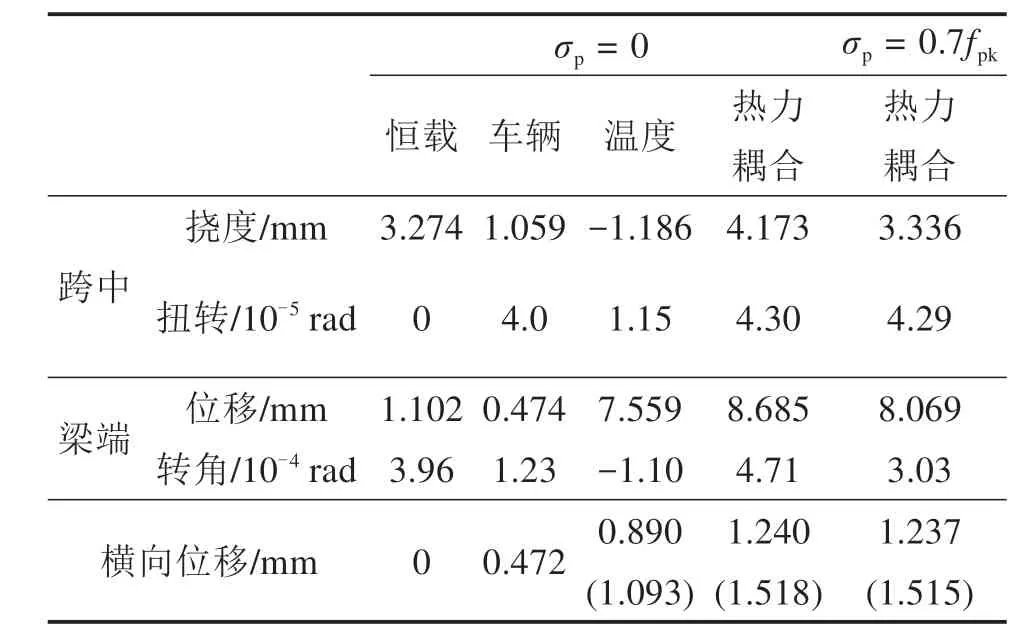
表1 轨道梁最大变形量Table 1 Maximum deformation of guideway

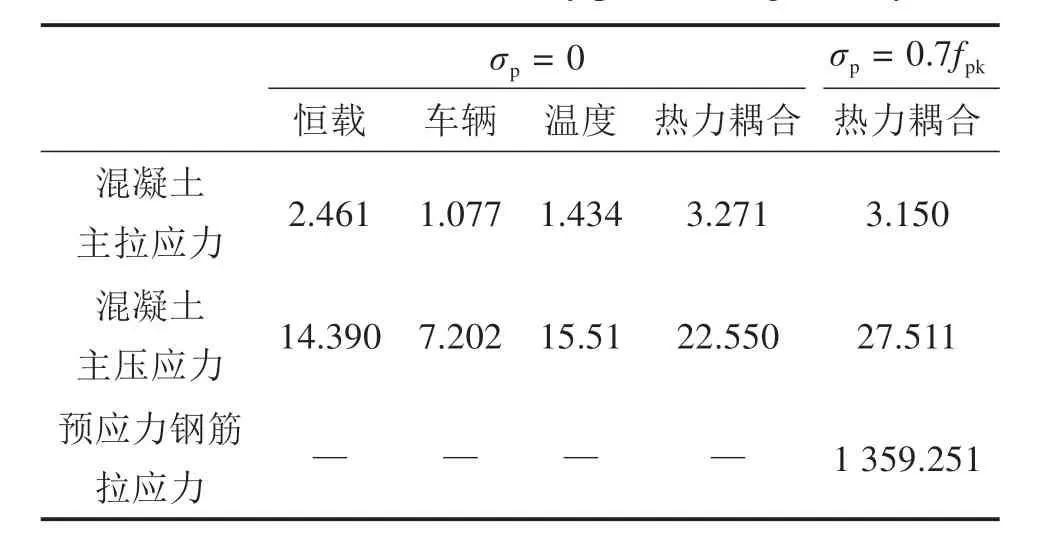
表2 轨道梁关键位置最大应力Table 2 Maximum stress at key position of guideway MPa

此外，热力耦合工况下，在凌晨01:00时有预应力轨道梁跨中挠度最大，最大值为3.366 mm。下午14:00时，轨道梁跨中挠度最小，最小值为3.150 mm。2种预应力水平下的轨道梁挠度最大值出现时刻一致，前者挠度比后者少23.96%，可见预应力可增加轨道梁竖向刚度[16]。轨道梁热力耦合横向位移极值出现时刻为上午11:00和下午15:00。位移极值分别为1.515 mm和1.237 mm。2种预应力水平下的轨道梁横向位移仅相差0.2%，可见预应力对轨道梁热力耦合作用下的横向变形影响不明显。

5 结论

1)整体式预应力混凝土轨道梁温度场最大竖向温差发生在14:00，自顶面向下发生15℃左右温差，且与规范建议温度单向减少的梯度不同，轨道梁自底向上0.3 m存在4℃温差；最大横向温差发生在11:00和15:00，靠近东西侧承重梁翼缘外表面横向温差大，中间位置小。

2)轨道梁在各工况下的变形及应力均满足规范强度、刚度限值要求。下午14:00时刻，轨道梁竖向温差引起的跨中挠度(上拱)最大，同时刻热力耦合工况下轨道梁跨中挠度最小。凌晨01:00时刻，轨道梁跨中挠度最大。横向位移极值分别出现在上午11:00和下午15:00。

3)预应力筋对轨道梁跨中竖向挠度影响显著，预应力水平为0.7fpk的轨道梁跨中挠度比无预应力的轨道梁要少23.96%；预应力筋对轨道梁横向变形影响不明显，预应力水平为0.7fpk的轨道梁横向变形与无预应力的轨道梁仅相差0.2%。