面向双向渐进结构拓扑优化法的高效灵敏度过滤算法研究
尉洋,王春彭,陈兴,曹月昊,姚松
(1.轨道交通安全教育部重点实验室,湖南 长沙410075;2.轨道交通安全关键技术国际合作联合实验室,湖南 长沙410075;3.轨道交通列车安全保障技术国家地方联合工程研究中心,湖南 长沙410075)
自1988年Bendsøe和Kikuchi提出均匀化拓扑优化以来,拓扑优化理论得到了巨大的发展[1],各种基于梯度的算法也相继提出,如变密度法(SIMP)[2-3]、水平集法(Level-set)[4]、双向渐进优化法(BESO)[5-6]以及近年提出的浮动投影方法(FPTO)[7-8]等。随着计算机性能的不断提升以及增材制造技术的逐步完善,拓扑优化已然成为结构优化设计领域中的热点问题[9]。拓扑优化的本质是凸优化问题,是在仿真分析的基础上,找到材料在设计空间当中的最优分布。拓扑优化技术应用在结构的概念设计阶段,能够突破传统优化手段的设计极限,最大限度地拓展设计空间[10]。在连续体结构拓扑优化过程中,经常存在着数值不稳定现象[11-12],如棋盘格和网格依赖性等问题。前者会导致拓扑结果可制造性降低,后者会使得计算结果不可靠。为了避免出现这些现象,可用的手段有:高阶单元法、周长约束法、局部梯度约束法以及网格过滤技术[13-14]。其中,过滤技术不需要在优化过程中加入其他约束,易于实现的同时计算稳定,被认为是最有前景的方法,得到了广泛的应用。网格过滤技术包括灵敏度过滤、密度过滤以及偏微分过滤,前2种是目前的主流过滤方法。灵敏度过滤是基于邻域单元的灵敏度大小对中心单元灵敏度进行修正,一般选用外接方形(二维)或外接立方体(三维)作为单元邻域,然后进行单元距离与权重的计算,如图1所示,关键一步是确定待过滤单元的邻域单元及其对应的权重系数。在规则网格的背景下,FERRARI发布的教育代码中给出了依据单元规则编号确定邻域单元及权重的方法[15],具有较好的效率,但其适用对象仅限于单元和节点编码按照预设规则设置的平面矩形结构。对于复杂结构,单元节点编码不再有序,其不再适用。另一种方法是利用枚举[16],结合单元形心间距通过循环来确定单元邻域,实现简单方便。然而实际上绝大部分单元不在过滤半径之内,浪费了大量的计算资源,其计算复杂度为O(n2),对于具有大量网格的模型而言,枚举的效率难以被接受。另外,当结构内部中存在有细小非设计域孔洞时,仅仅通过单元形心距离确定中心单元邻域的做法,无法准确判断单元之间的连通性以及识别孔洞边界,以至于得到不准确的单元邻域。为了准确快速找到过滤单元的邻域,减少前处理阶段中过滤算法的耗时,探寻解决细小非设计域孔洞问题的方法,针对BESO法,本文提出一种快速搜索策略,能够适应任意非规则网格且易拓展至三维。相对于枚举策略而言,能够显著提高搜索效率。通过计算表明,在设计空间中存在微小非设计域孔洞的情况下,使用这种过滤策略的BESO法能得到性能更优的拓扑构型。

图1 灵敏度过滤技术Fig.1 Sensitivity filtering method
1 BESO法
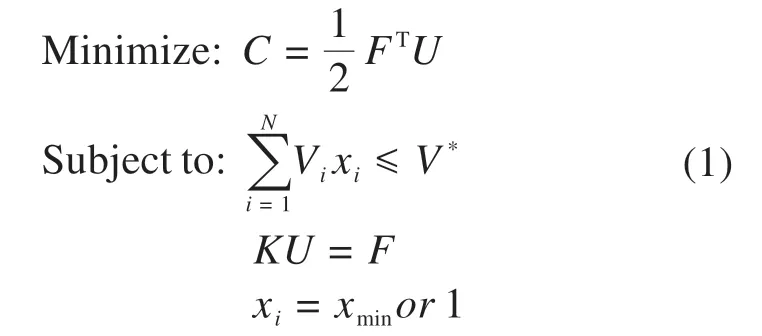
以实际常见的受到体积约束的刚度最大问题为例,建立基于BESO法的求解模型如下:其中:C为结构柔度;F为外载荷向量;U为节点位移向量;V*为结构体积约束上限;N为单元个数;Vi为单元体积;K为结构整体刚度矩阵。xi为设计变量,表示单元的相对密度,实体单元取值为1,为了保证整体刚度矩阵的非奇异性,空单元取较小值xmin,一般为0.001。
引入材料插值方案:

E0表示实体材料的弹性模量;p为惩罚系数,一般取值为3。通过伴随法和链式求导法则求得目标函数关于设计变量的灵敏度为:

其中:K0i为实体状态下的单元刚度矩阵。
优化迭代停止条件为:在过去10次迭代中,结构柔度的变化足够小。
2 利用节点单元从属关系确定单元邻域
式(3)所求得的单元灵敏度在直接使用时会存在着显著的数值不稳定现象,使得结构中出现棋盘格或网格依赖性等问题。为了避免这些现象出现,需要进行灵敏度过滤。
灵敏度过滤公式为:
其中:Hij为权重因子,计算公式为:

d ist(i,j)表示单元i的中心到单元j中心的距离;rmin是过滤半径。
对于拓扑优化过滤技术而言,最为关键且耗时最长的部分在于确定单元的搜索邻域N,本文提出一种利用从中心单元——从属单元——邻域单元的逐层搜寻模式快速准确地搜寻求解。
当结构建模、网格划分完成之后,有限元模型中会储存有表示节点位置的节点-坐标信息、单元所有节点的单元-节点信息E={n1,…,nNe},通过E可以方便地推导出节点所在单元的节点-单元信息N={e1,…,eNn}。其中,ni表示单元i中节点的编号(i=1,…,Ne,Ne为结构中单元数);ej表示节点j所属单元的编号(j=1,…,Nn,Nn为结构中节点数)。定义f为e到E的一个映射,g为n到N的一个映射,即:

其中:unique为去除集合中重复单元。
以如图2的二维四边形单元为例。首先确定中心单元ei,通过单元-节点信息找到单元ei包含的节点(ni1,ni2,ni3,ni4),通过节点-单元信息找到扩充后的单元编号,如式(6)所示。循环所有设计域单元组合后得到每个单元的相邻单元信息,至此构建出中心单元与从属单元之间的联系,如式(7)所示。当过滤半径给定时,反复索引调用式(7)使得搜索范围向外辐射,通过自适应收敛条件能够针对不同网格密度区域设置合理的迭代层数,便能迅速确定单元邻域,最终构建出从属单元到邻域单元之间的联系,如式(8)和式(9)所示。收敛得到的邻域单元去除重复之后即为该单元的最终搜索邻域。

图2 快速寻找单元邻域Fig.2 Fast search elements neighborhoods
网格过滤算法来源于数字图像处理中的降噪技术,应当考虑结构或单元之间的连通性。当结构中出现有细小非设计域孔洞时,传统过滤策略若要准确识别,需要在搜索过程中反复调用和读取结构的实际边界信息,代码实现繁琐,显著增加编程难度。一般的做法是按单元形心间距离进行搜索,不考虑孔洞所带来的影响,如图3(a)所示。

图3 含微小非设计域孔洞时传统策略与新策略的比较Fig.3 Comparison of traditional and new strategies when there are small non-design domains holes
对于这种情况,新策略有天然的优势:有限元模型中的单元-节点信息和节点-单元信息已经包含了结构实际边界信息,当搜索到几何边界时,若要继续进行,由于孔洞没有单元,因此搜索区域不会越过细小孔洞,从而得到相对正确的单元邻域,如图3(b)所示。
3 新策略灵敏度过滤流程
图4展示了运用新策略进行灵敏度过滤的详细流程图。

图4 新策略灵敏度过滤流程图Fig.4 New strategy sensitivity filtering flow chart
4 过滤策略的比较
本节从网格适用性、过滤用时以及带初始设计孔洞3个方面比较几种过滤策略的优劣,均选择使用Python语言在ABAQUS平台上进行二次开发,ABAQUS版本为2016,拓扑优化算法为BE‐SO法。
4.1 网格适用性
依据规则编号确定单元邻域具有非常大的局限性,即仅适用于规则网格,在非规则网格或任意网格的背景下公式法无法适用。枚举的方法能够适应任意网格,并已经得到了广泛的应用。利用新策略寻找邻域的策略也能适应任意网格,可直接应用至三维结构。
4.2 计算用时
选择5种不同规模的立方体网格数量,取10次过滤耗时的平均值做比较(不含导出单元−单元信息时间),计算环境为Lenovo Y7000 2020,Intel 10750处理器,16 GB内存,在win10系统下,Python版本为3.7,耗时如表1所示。分析可知,仅在过滤半径内的单元才会对中心单元的灵敏度产生影响,处于过滤半径之外的单元对其灵敏度影响为0,而邻域单元相比设计空间而言数量很少,由此可见,利用枚举直接计算方法会极大浪费计算资源。

表1 2种策略在不同网格数量下的计算耗时Table 1 Calculation time of the two strategies under different number of elements s
以一桥梁结构优化设计[17]为例,进一步比较2种策略的计算用时:结构初始设计如图5所示,为便于行人和车辆通过,留有一层厚度为0.6 m的非设计域。由于对称性仅计算1/4模型,单元尺寸为0.2 m,划分为147 500个单元,弹性模量为20 GPa,泊松比取0.2。体积分数为设计域的10%,目标为结构刚度最大,删除率取5%,添加率最大为5%,过滤半径为0.6 m,收敛容差为0.01,有限元过程采用6核并行计算。

图5 设计域与非设计域、几何尺寸及边界条件Fig.5 Design and non-design domains,geometric dimensions and boundary conditions
优化结果如表2所示,运用2种策略进行优化迭代次数相同,有限元用时及最终构型相似,柔度一致。但对比过滤及有限元用时可知,虽只在优化开始时组成过滤权重矩阵,但当问题扩大到一定规模之后,这仅仅一次的邻域搜索会消耗大量的计算时间,远超有限元迭代用时,相比而言本文策略具有显著优势。

表2 2种策略优化结果对比Table 2 Comparison of the optimization results of the two strategies
4.3 设计域存在微小孔洞的柔度优化问题
以一个三维算例来对比说明新策略在初始设计中有微小非设计域孔洞时的适用性,优化背景为考虑在一定体积约束下柔度最小问题。几何结构如图6所示。
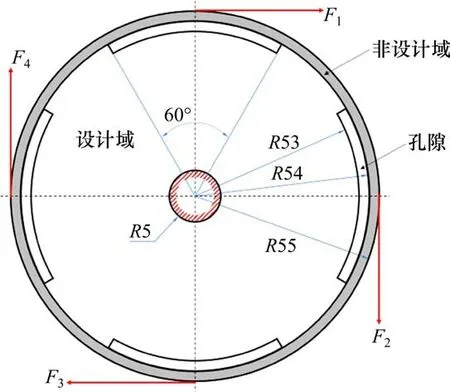
图6 优化初始构型Fig.6 Optimized initial structure
圆盘厚度为10 mm,半径为55 mm,中间挖有R5 mm的通孔,距离受力位置1 mm处各有一圆心角为60°,厚度为1 mm的细小缝隙,贯穿圆盘。结构约束及载荷如图6红线所示,灰色部分为非设计域,中间圆柱面固定,周围分布有4个线均布力,力的大小为110 N。有限元离散采用的单元尺寸为1 mm,材料弹性模量为210 GPa,泊松比为0.3。考虑目标体积约束为20%,删除率取1%,添加率最大为1%,过滤半径为3 mm,收敛容差为0.001。
图7显示了运用2种不同的策略对圆盘进行优化得到的最终拓扑结构,新过滤策略能够很好地避免数值不稳定的现象,得到理想的拓扑构型,如图7(a)。枚举过滤策略得到的结构大体相同,如图7(b),但是在缝隙周围出现了“孤岛”的现象,这是由于缝隙外层单元在载荷附近,位移较大,因此单元灵敏度相对较大,枚举时外侧单元的影响会越过缝隙,使得缝隙内侧单元加权后的灵敏度也相对较大,以至在优化过程中不会被删掉。而运用新策略搜索邻域时,缝隙外边的单元不在内侧单元邻域范围内,因此不会出现上述情况。
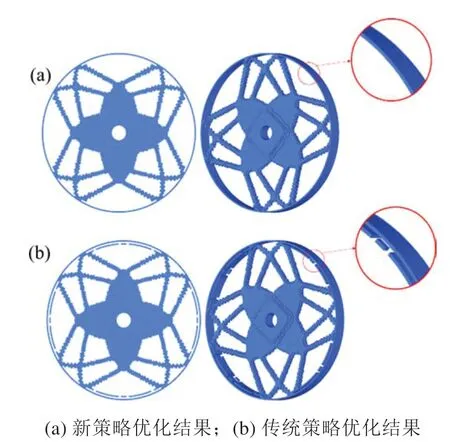
图7 2种策略最终拓扑构型Fig.7 Final topology of the two strategies
图8给出了2种策略的优化迭代曲线,显然,由于消除了“孤岛”现象的存在,新策略得到的最终拓扑构型柔度要低于枚举策略所得到的结构,性能差别达到4%。
5 结论
1)提出一种利用节点单元从属关系快速确定单元邻域的策略,通过建立中心单元——从属单元——邻域单元的逐层搜寻模式迅速确定单元邻域,减少了搜索范围,其搜索速度与枚举策略相比有较大优势。
2)新策略的实现过程简单方便,能够适应任意网格并且容易拓展至三维结构,结合此策略的过滤算法能够有效抑制棋盘格和网格依赖性的现象。
3)对于初始结构设计中含有微小非设计域孔洞的问题,基于BESO法,使用新策略确定的单元邻域进行后续优化时的结果能够有效消除结构中的“孤岛”现象,相对于传统策略,新策略能够得到性能更优的构型。

