一种面向孔洞修复的三角网格复杂孔洞分割方法

张善辉 武伟 魏威 边静

（1.山东大学控制科学与工程学院 山东省济南市 250061 2.山东山大华天软件有限公司 山东省济南市 250101）

1 引言

三角网格具有简洁、直观、描述能力强的特点，是一种应用十分广泛的几何模型表达形式，逐渐成为3D 打印技术的重要应用基础。但是，在网格模型的构建和获取过程中，经常会产生各类网格模型的孔洞，严重影响了3D 打印模型的外观和质量。因此，三角网格模型中孔洞的识别和修复成为提高3D 打印质量的关键。

目前，国内外许多学者对三角网格模型的孔洞修复方法进行了深入研究，其中比较典型的修复方法为：根据孔洞的点分布，计算特征平面，将孔洞点投影到特征面上进行分元，然后采用隐式函数[1]、径向基函数[2,3]、波前法[4]等，将特征面上的点映射到三维模型上。该类方法得到的填孔面的形态往往比较理想，但适用场景较为苛刻，在简单孔洞形态下能够获取理想的效果，但对复杂孔洞形态可能出现映射失败或者映射错误的情况，导致填孔效果差。学者Jun[5]提出一种将复杂孔洞剖分为简单孔洞再进行修补的算法，解决了投影过程中具有自相交边界的孔洞剖分和修补，但在处理其他类型复杂孔洞及修补效果方面，特别是非投影过程的自相交边界问题，并不是很理想。学者温佩芝提出一种缺陷孔洞自动识别与孔洞区域细节特征保持的曲面修复方法，但方法仅适用于单连通区域的缺陷孔洞修复，忽略了复杂缺失区域的拓扑结构，且算法的时间复杂度也较高[6]。Chao Feng 提出一种根据三角网格孔洞顶点的规模进行孔洞分类的方法，并分别采用不同的修复方法，可以实现快速孔洞修复，但分类方法中仅仅考虑孔洞大小，忽略了孔洞的复杂拓扑形态，不能很好的解决复杂孔洞的修复效果[7]。

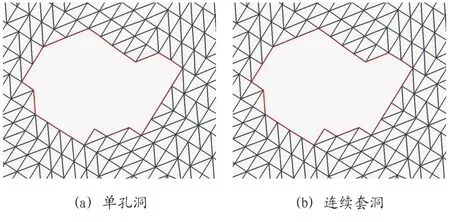
图1：单孔洞与连续套洞的示例图

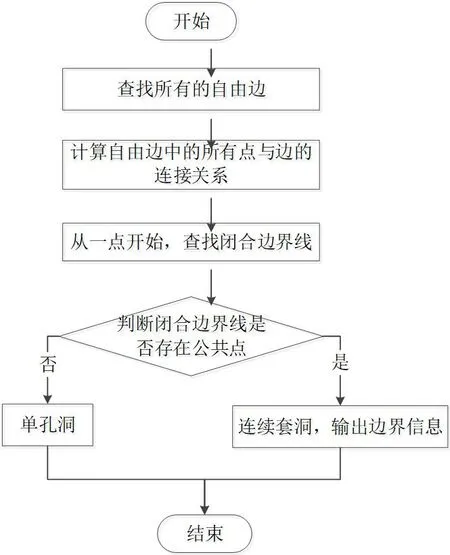
图2：单孔洞与连续套洞的识别流程

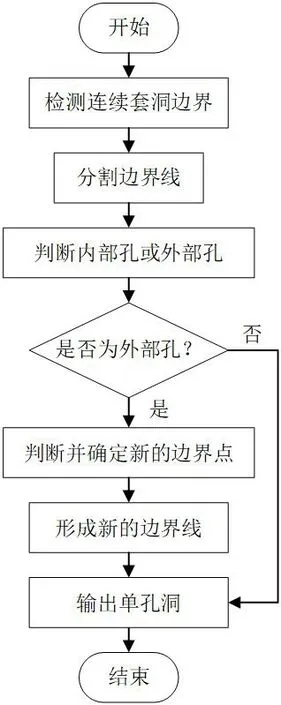
图3：连续套洞的分割流程

图4：外部孔洞线下一边界点的判断

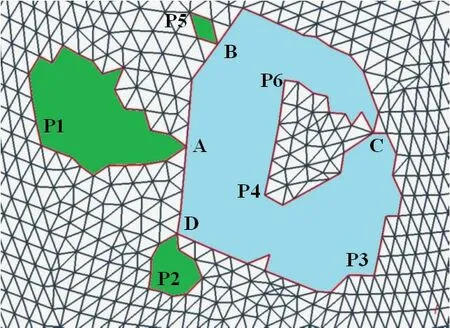
图5：单孔洞的识别与输出

综上所述，当前的三角网格模型修复大多集中于修复方法的研究，在对复杂孔洞的分割处理方面还存在欠缺。因此，为实现复杂孔洞的修复，本文从各类孔洞的拓扑形态出发，首先解决复杂孔洞的识别与分割问题，将其划分为单孔洞和连续套洞两类，并针对形态复杂的连续套洞嵌套、交叉特点，提出一种对三角网格模型孔洞进行检测、识别和分割的方法，将连续套洞剖分为单孔洞，弥补了各类孔洞修复方法在复杂孔洞修复中的不足。

2 单孔洞与连续套洞

2.1 单孔洞与连续套洞的特点

通过统计和分析三角网格模型中各类孔洞修复的失败案例发现，修复失败现象常常发生在多个孔洞相邻的情况下，易造成各类孔洞映射失败或者映射错误，进而导致修复效果不理想。为解决这一问题，需要分析此类孔洞的特点，总结其与单孔洞的差别。通过大量案例的分析，发现单孔洞与此类孔洞的主要区别为：是否存在多个孔洞线的公共点。为此，定义如下两类孔洞：

图6：某商业软件的孔洞识别效果

图7：案例示意图——背包

定义1：单孔洞——孔洞线上的点可以依次连接组成一条唯一解的闭环。如图1(a)所示。

定义2：连续套洞——由多个单孔洞组成，且它们的孔洞线上的点存在公共点，导致其具有多种表示各个单独闭环的方法。如图1(b)所示，连续套洞的A、B、C、D 四点均为多条孔洞线的公共点，以逆时针方向为正，可以识别出此连续套洞的孔洞边界为A-P1-AB-P5-B-C-P6-P4-C-P3-D-P2-D-A。

2.2 单孔洞与连续套洞的识别方法

由于单孔洞和连续套洞在三角网格模型孔洞修复中的难度差异较大，采取的修复方法各不相同。因此，对所有的孔洞进行分类识别，确定其是否为单孔洞或连续套洞，这是孔洞修复的必要步骤。在识别之前，需要对输入的三角网格模型进行预处理，快速建立模型的面片、边和顶点的拓扑结构；根据三角网格模型的面片与边的连接关系，获取三角网格模型的所有单连通区域，将每个单连通区域视为一个部件；对每个部件查找自由边，根据边与点之间的连接关系，将所有的自由边首尾连接，得到孔洞线，即获得所有孔洞的基本信息，包括孔洞线、孔洞方向和孔洞与部件之间的关联关系。其中，自由边是指仅连接一个面片的边；孔洞线是指在保持原始三角网格模型拓扑关系的基础上，将每个集合中自由边的首尾连接，所形成的闭合线。

在此基础上，构建了单孔洞与连续套洞的识别流程，如图2 所示。首先，通过所有获取孔洞的基本信息，查找孔洞线的所有自由边；查找自由边的集合，根据各条边和顶点的拓扑结构关系，计算自由边中的所有点与边的连接关系；从任一点出发，依据连接关系，查找闭合边界线；随后，判断闭合边界线是否存在公共点，如果不存在公共点，则输出单孔洞，如果存在公共点，则为连续套洞，输出其对应的边界信息，为后续的连续套洞的分割提供服务。

3 连续套洞的分割方法

为方便三角网格模型的修复，必须把复杂的连续套洞分割为简单的单孔洞，提高各单孔洞修复算法的准确率和修复质量。由于连续套洞存在孔洞线的嵌套和连接，容易造成多个孔洞的分解存在误差或错误。为此，研究提出了一种基于公共点的连续套洞孔洞线的分解和重构方法。具体步骤如图3 所示。

第一步，检测连续套洞边界。根据孔洞识别的信息，检测连续套洞的孔洞边界，按照逆时针方向，形成对应的孔洞线。例如图1(b)中的边界为A-P1-A-B-P5-B-C-P6-P4-C-P3-D-P2-D-A，识别出相同的面片点索引，即为公共点，如图1(b)中的A、B、C、D 四点。

第二步，分割边界线。根据连续套洞的公共点，将连续套洞的内部区域分割为若干个独立的孔。例如图1(b)中的连续套洞边界，可分割边界线得到五个单独的孔洞，分别为A-P1-A、B-P5-B、C-P6-P4-C、D-P2-D、A-B-C-P3-D-A。

第三步，判断内部孔或外部孔。将孔洞线上的点投影到平面上，根据点与多边形的内外关系，计算各个孔洞的内外位置关系；如果某一孔洞L1 的点均在另一孔洞L2 外部，则认为是L1 在L2 外。如果一条孔洞线不在任一个孔洞线内部，则该孔洞线为外部孔，如果一条孔洞线在某一个孔洞线内部，则该孔洞线为内部孔。

第四步，条件判断——是否为外部孔。如果外部孔不包含内部孔，则跳转到第七步；否则，继续执行第五步。判断可知，图1(b)的连续套洞中外部孔有A-P1-A、B-P5-B、D-P2-D、A-B-C-P3-D-A，内部孔有C-P6-P4-C，它被A-B-C-P3-D-A 外部孔包含。

第五步，判断并确定新的边界点。对于包含内部孔的外部孔，查找其孔洞线中的公共点，计算公共点和公共点连接的其它孔洞的索引点连线与公共点和当前外部孔洞线的前一索引点连线的夹角，选择夹角最小的这一索引点作为新的边界点。例如图4 中的C 点，通过计算夹角可知，∠1C2 小于∠1C3，判断其下一边界点为射线C2 方向，即P6 方向，而不是P4 方向。

第六步，形成新的边界线。从新的边界点开始，将内部孔上的点按照边界上的连接顺序全部插入外部孔的边界线中，合并孔洞外边线和内边线。即示例中，将内部孔C-P6-P4-C 插入到外部孔A-BC-P3-D-A 中，得到新的边界线为A-B-C-P6-P4-C-P3-D-A。

第七步，输出单孔洞。将所有满足条件的孔洞作为一个单孔洞输出，并给出边界线。根据此方法，示例中输出四个单孔洞，边界线分别为A-P1-A、B-P5-B、D-P2-D、A-B-C-P6-P4-C-P3-D-A。如图5 所示的填充区域，即为四条边界线所围成的四个单孔洞。

对比传统的孔洞识别方法和软件，此案例的孔洞容易将C-P6-P4-C 识别为单孔洞，并输出。依据此种结果填充后，所得模型将不是期望的结果，并且会产生大量的自相交面片。如图6 所示，绿色孔洞线和红色孔洞线均为识别的单孔洞，但是内部的红色孔洞线在修复时会与外部的孔洞线发生自相交，这显然与实际孔洞不符。

4 系统实现与验证

通过上述对三角网格模型孔洞的识别及连续套洞的分割方法的研究，采用效率更高的C++语言，开发实现了相应的孔洞分割功能，为后续的模型修复提供更加简便的单孔洞，便于模型修复准确性和效果的提升。此功能也已经成功在某模型修复组件中进行了应用，达到了处理复杂孔洞分割的目的。例如图7 中的背包模型，具有复杂的孔洞类型，包含了多个单孔洞和复杂的连续套洞。通过孔洞识别方法可以识别出所有的单孔洞和连续套洞。图中，红色线条代表连续套洞，绿色线条代表单孔洞。背包中共识别出两组连续套洞，即点画线所包围的区域。借助连续套洞的分割方法，可以将上部的连续套洞合并为一个完整的单孔洞，下部的连续套洞可以分割为5个单孔洞。由此可以验证，本方法可以适用于复杂孔洞的识别和分割，为后续的孔洞修复提供了有效的模型预处理功能。

5 总结

从三角网格模型孔洞修复效果不佳的角度出发，发现了孔洞形态对修复效果的影响。通过分析各类孔洞的特点，将孔洞划分为单孔洞和连续套洞，并给出了对应的孔洞识别方法；针对连续套洞孔洞线的嵌套和连接特点，提出了一种基于公共点的连续套洞孔洞线的分解和重构方法，解决了连续套洞输出为单孔洞的问题，避免了孔洞修复中常见的自相交面片的出现。通过实例和软件验证，此识别和分割方法可以对三角网格模型的复杂孔洞进行预处理，极大的提高了模型修复的效果和质量，可以广泛应用于3D 打印模型修复业务中。