非对称液压缸系统键图建模与仿真分析
叶正茂,衣 超
(1.哈尔滨工业大学 机电工程学院,黑龙江 哈尔滨 150001;2.中国北方车辆研究所 车辆传动重点实验室,北京 100071)
为了实现长圆柱型试件的摇摆运动模拟,试验台采用了对称伺服阀差动控制两个非对称液压缸进行驱动的结构形式,通过精确控制液压缸的差动运动达到控制试件摆动角度的目的。其结构示意图如图1 所示,通过液压缸的伸缩运动,实现试件的摇摆运动。系统液压控制原理图如图2 所示,一个液压缸无杆腔与另一个液压缸的有杆腔通过液压管路连通,当一个液压缸活塞杆伸长时,另一个液压缸活塞杆缩回。
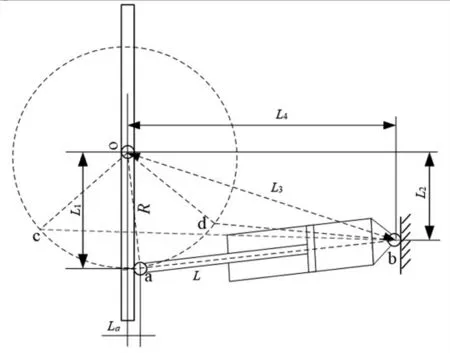
图1 结构示意图

图2 液压原理图
其工作原理为:当系统不工作时,伺服阀块锁紧装置锁住液压缸,使试件保持在初始位置静止。当系统通电,控制系统启动液压源并加压,锁紧装置解锁打开,系统液压缸处于位置闭环状态。通过用户给定期望的运动参数,利用计算机实时计算出伺服驱动器的位移量,输入到伺服驱动系统,实时控制液压缸伸缩驱动试件摆动,摇摆角度由液压缸位移传感器测量值解算获得,并反馈到控制计算机,从而实现试件高精度姿态控制。
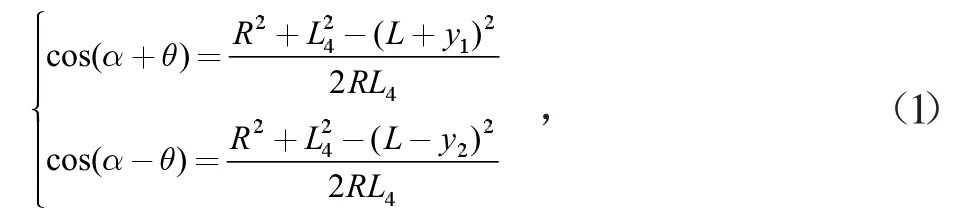
摇摆架的摆角与两液压缸伸长量的关系为:其中,夹角α=∠aob,θ 为试件摆角。
由式(1)可知,因为结构限制,连接铰点与回转轴之间具有水平距离La,导致一定摆动角度下两液压缸活塞杆伸出和缩回运动的行程不同,速度也不相同,同时进入两液压缸的流量也不相同,系统具有较大的非线性。
1 系统的键图模型
键图又称为键合图或者功率键合图,键图建模方法适用于研究工程系统的动态性能,可以很方便地建立具有非线性系统的数学模型[1]。根据键图基本原理,采用20-sim 软件,可以建立本文所研究系统的键图模型[2-3]。
伺服阀的键图模型如图3 所示。模型中考虑了伺服阀的死区特性、饱和特性和动态响应特性,分别采用20-sim 中的死区模块、饱和模块和动态特性模块描述。4 个R 元,描述了伺服阀流量和压差相关的非线性特性,还可以研究4 个阀口不匹配对称情况下的系统特性,更符合实际的伺服阀特性。
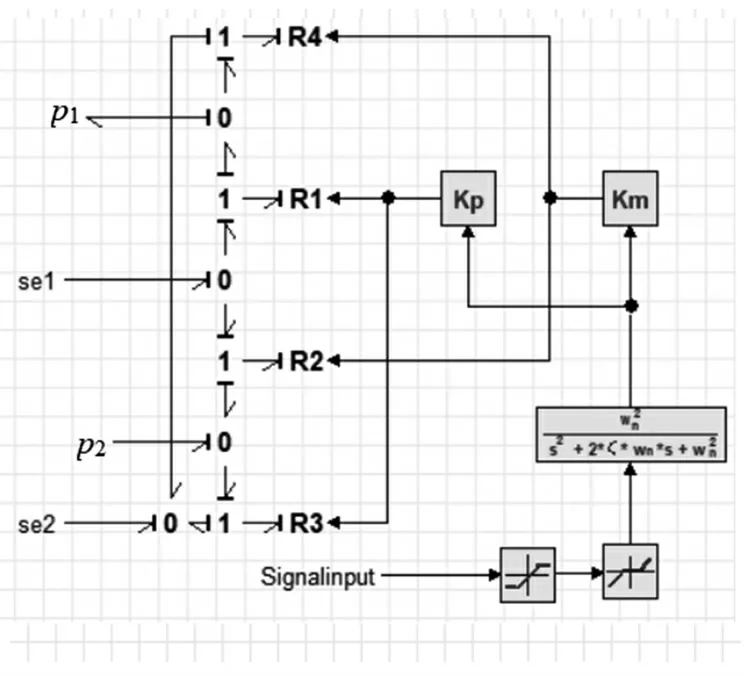
图3 伺服阀的键图模型
非对称液压缸的键图模型如图4 所示。模型中的C元,表示的是液压缸容腔的液压弹簧。模型中考虑了随着液压缸活塞位置变化时,液压缸两个容腔体积的变化情况,体积变化直接影响液压缸的液压弹簧刚度值,体现了液压弹簧的非线性特性。
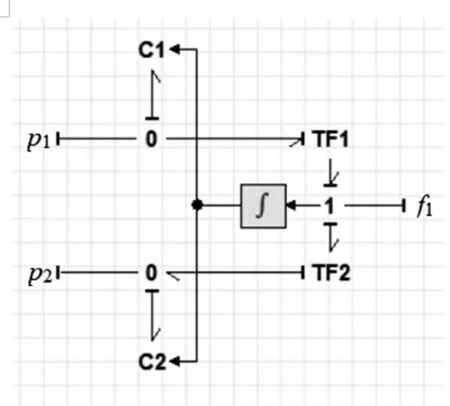
图4 非对称液压缸的键图模型
系统整体键图模型如图5 所示。
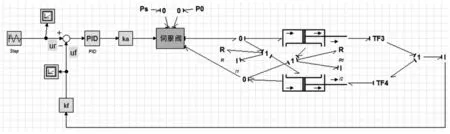
图5 系统的整体键图模型
系统整体模型中,既包含键图模型部分,也包含反馈模块、控制模块等部分,通常称这样的模型为扩展键图模型。将伺服阀模型和液压缸模型建立为子模型,以使模型看起来更加简洁。
整体模型中,还考虑了两个液压缸之间连接软管的阻尼特性和液压油的惯性,分别用R 元和I 元表示。该系统具有较长的液压管路,对系统动态特性有较大影响。
元件TF3和TF4两个变换器,其方程为:
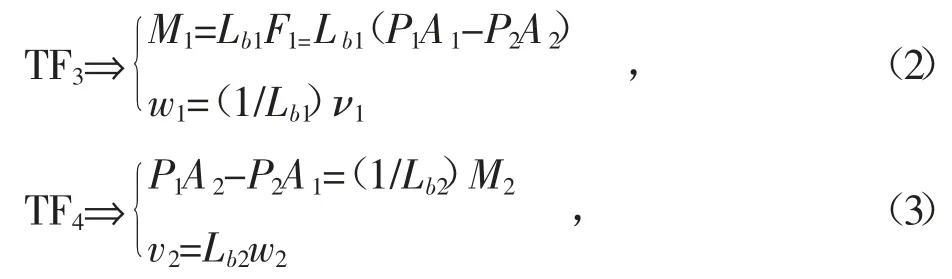
式中,Lb1和Lb2为液压缸活塞杆的驱动力臂,力臂的变化也具有明显的非线性特性。
液压缸伸长时,夹角β1=∠cbo,
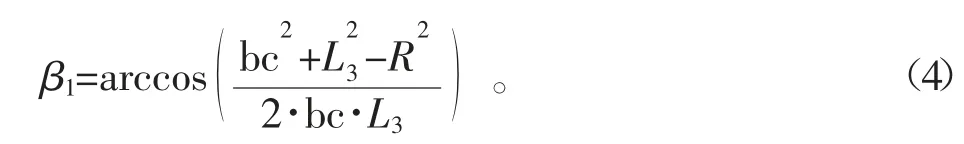
液压缸伸长时驱动力臂:

另一个液压缸缩回时,夹角β=∠dbo,
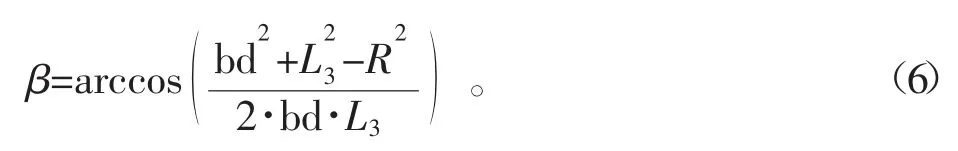
另一个液压缸缩回时的力臂:

根据式(2)至式(7),可以看出TF3 和TF4 两个变换器,是非线性变换器。这两个变换器体现了液压缸的直线运动和试件转动的关系,以及液压缸的直线驱动力和试件驱动力矩的关系。
2 仿真分析
扩展键图模型采用PID 控制,系统输入为幅值π/12 rad,频率0.2 Hz 的正弦期望信号,采用20-sim 软件进行仿真,仿真结果如图6 至图9 所示。

图6 角度跟随曲线

图7 液压缸线速度曲线
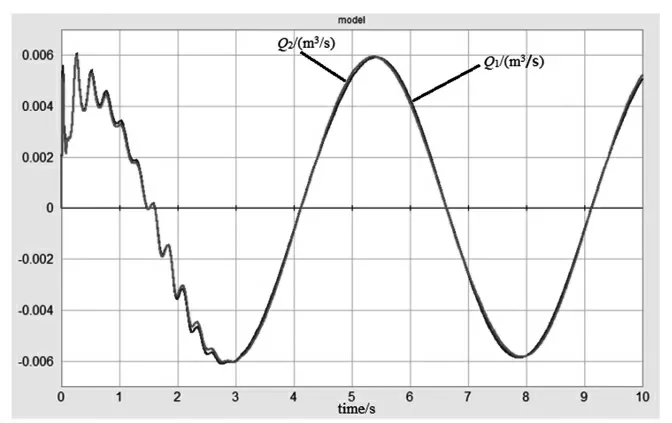
图8 伺服阀AB 口流量曲线
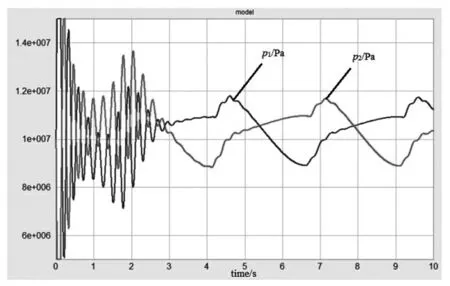
图9 液压缸AB 腔压力曲线
由图6 可见,试件输出信号相位滞后为13.14°,幅值衰减12.64%。通常系统定义为:相频宽是-90°滞后,幅频宽是衰减-3 dB。这说明系统可以跟随0.2 Hz 信号。
由图7 可见,两个液压缸的线速度不相等,说明活塞杆伸出和缩回速度不同,但是相差不大。这也说明液压缸活塞杆伸出和缩回是不对称的,具有明显的非线性特征。
由图8 可见,伺服阀A、B 口流量不相等,但是差别不大。这是因为液压缸伸出和缩回速度不相等导致的。
液压缸C 元的初始压力值设定为10.5 MPa。由图9 可见,因负载加速度较小,仿真曲线稳定后,液压缸压力值约在9~12 MPa 之间变化。
模型初值设定后,仿真初始段,存在一段仿真数据收敛过程,这导致图7 至图9 前3 s 的曲线波动较大。
3 结论
本文建立了具有非线性特性的阀控非对称液压缸系统的键图模型,并进行了仿真分析。
建立的系统键图模型考虑了伺服阀的死区非线性、饱和非线性及流量非线性等非线性因素;考虑了液压缸的容腔体积变化导致的液压弹簧刚度变化的时变非线性因素;考虑了液压缸和伺服阀之间连接管路的阻尼特性和液压油惯量的影响;考虑了系统机械结构导致液压缸驱动负载具有的本质非线性因素。
与传递函数模型相比,键图模型更适用于建立具有非线性特性、时变特性等非线性特性的系统数学模型,开展系统的时域特性仿真分析。

