基于升沉补偿平台多缸同步的控制策略研究

潘梦婷，张冰，赵强，周萌萌，左思雨

(江苏科技大学海洋学院，江苏镇江 212100)

0 前言

升沉补偿平台是一种机电液一体的装置，以6个液压缸并联作为补偿执行器，通过控制6个液压缸运动驱动上平台稳定补偿船舶在海上作业时因风浪作用所产生的不规则运动。任何一个液压缸的位移发生变化都会导致升沉补偿平台的上平台发生一定角度的倾斜使平台不平稳，因此为实现升沉补偿平台的精确控制和稳定运作，必须同步控制6个液压缸。

目前，对于多液压缸的同步控制主要有非耦合控制和耦合控制两种同步控制方式。相较于非耦合控制，耦合控制方式在有干扰的情况下依然具有较好的响应速度和同步控制精度，它在电机的同步控制中应用较多，对于多缸同步的工程应用实例较少。文献[3]将环形耦合同步控制策略应用于电机传动系统，考虑电机本身的速度误差以及相邻电机的速度误差，采用模糊PID控制算法对电机速度进行控制，提高了系统的一致性和稳定性。文献[4]将PID控制与环形耦合同步算法相结合，提高了四缸同步的有效性。文献[5-6]采用相邻交叉耦合同步控制方式，考虑自身液压缸的跟踪误差以及与相邻2个液压缸的同步误差，前者采用双模糊控制器补偿系统同步的大范围误差，后者采用模糊PID控制算法获得难以通过常规方法获得的精确的补偿系数，提高了四缸同步控制性能。文献[7-8]采用不同的耦合方式结合相同的预测控制算法对不同的系统进行了同步控制，都在各自的代价函数中引入了同步误差项，提高了系统的鲁棒性和同步控制性能。

本文作者以升沉补偿平台中6个液压缸并联运动为研究背景，针对平台液压系统存在的非线性、参数时变性等特点，提出一种基于广义预测控制算法的多液压缸相邻交叉耦合同步控制方法。采用广义预测控制算法控制单个液压伺服通道，计算作用于单个液压伺服通道的控制量；采用相邻交叉耦合的同步控制方式，建立自身液压缸以及与相邻2个液压缸的同步误差，将同步误差反馈作用于自身液压伺服通道，获得新的控制律，实现对6个液压缸的位置输出同步控制，减小输出不同步对升沉补偿平台平稳运作的影响。

1 平台液压伺服系统数学模型

1.1 升沉补偿平台液压伺服系统

升沉补偿平台有6个相同的液压伺服系统，每个伺服通道均由伺服放大器、电液伺服阀、非对称单出杆液压缸、位移传感器组成，分别构成6组相同的闭环回路。根据给定的位姿信号与位移传感器测得的实际液压缸的位移信号构成偏差，由伺服放大器将偏差信号转换为电液伺服阀所能接受的电流信号，控制伺服阀阀芯运动以控制流向液压缸的油液流量，从而实现对液压缸位移的控制。平台的液压伺服系统如图1所示。

图1 升沉补偿平台液压伺服系统

1.2 液压伺服系统数学模型

由于6个液压伺服闭环回路相同，每个液压伺服通道的数学模型相同。其核心部件均为电液伺服阀控非对称液压缸，结构如图2所示。

图2 阀控非对称液压缸

液压伺服系统的数学模型可以根据阀控非对称液压缸的3个基本方程以及其主要元件的传递函数建立。文献[10]对于3个基本方程的推导有非常详细的过程。

每个液压缸的传递函数为

(1)

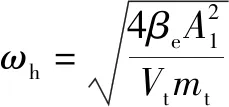
伺服放大器和位移传感器均可视为比例环节，分别表示为、。电液伺服阀的传递函数为

(2)

式中：、、分别为电液伺服阀的流量增益、固有频宽和阻尼比。

因此，每个液压子系统的位置传递函数的表达式为

(3)

2 控制器设计

对于所提系统，其扰动是非平稳的，所以采用受控自回归积分滑动平均(Control Auto-Regressive Integrated Moving Average,CARIMA)过程模型描述液压伺服系统的数学模型。

首先，将每个液压伺服系统离散化，得到差分方程：

()+(-1)+…+(-)=()+

(-1)+…+(-)

(4)

式中：()、()分别表示每个液压伺服系统的输出和输入(控制量),=1，…，6；,,…,和,,,…,为系统系数；、分别为输入和输出的阶次。由式(4)可确定()和()：

故每个液压伺服子系统的CARIMA模型为

()()=()(-1)+

()()(1-)

(5)

式中：()为随机干扰噪声；(1-)为后移算子。

针对式(5)求解相邻交叉耦合后作用于每个液压伺服系统的控制增量Δ()，使它在保证单个液压伺服通道控制性能稳定的情况下，对控制量进行优化，从而使6个液压伺服通道相互之间的同步误差趋向于0。

讨论()=1时对系统的控制,对+时刻的6个液压伺服子系统的输出进行预测，引入丢番图方程：

(6)

()、()、()、()均可以通过递推计算得到，其表示形式为

由式(5)、式(6)可得到每个液压子系统提前步的最优预测输出模型为

(+|)=Δ(+-1)+Δ(-1)+

()

(7)

式中:Δ(+-1)为每个液压缸未来控制增量;Δ(-1)为过去的控制增量;()为过去输出。

系统的最优预测输出模型的矩阵形式为

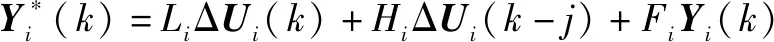
(8)

由于式(8)中的后两项依赖于液压伺服系统过去时刻的输入和输出，因此令:

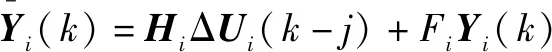
(9)

由式(8)、式(9)得到每个液压子系统最优输出预测值的矩阵形式为

(10)

式中:

为减少系统的超调以及使曲线平滑，对参考轨迹进行滤波处理，其形式为

(11)

式中：为设定值；为平滑后的位姿设定值;(0<<1)为影响液压伺服系统动态响应的平滑因子。

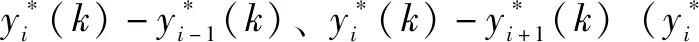
为使液压系统的输出()能够自动、快速而准确地跟踪参考轨迹(+)，选取的二次性能指标函数包含自身的跟随误差、控制增量以及自身液压缸分别与其相邻2个液压缸之间的同步误差，表达形式如下：

(12)

式中:为数学期望;、为影响同步误差的补偿系数，适当增大同步补偿系数可减小同步误差；为影响跟踪误差的控制加权因子，当>0时，性能指标函数可表示为如下矩阵形式：

(13)

式中:()=[(+1),(+2),…,(+)]为未来期望输出向量。通过将性能指标函数极小化可求得每个液压伺服系统的控制增量Δ()。为计算简便,以液压伺服通道6为例求其控制量，此时的性能指标函数包含液压缸6分别与液压缸1和液压缸5之间的同步误差项，其矩阵形式为

(14)

由式(10)、(11)将式(14)极小化，得到如下形式：

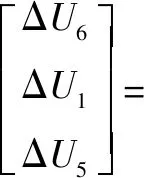
(15)

取式(15)矩阵的第一行记为液压伺服通道6的控制增量Δ()，则得到时刻液压伺服通道6所需的控制量为过去时刻控制量和当前时刻控制增量的和,即为

()=(-1)+Δ()

(16)

以此方式类推，即可得到其余液压伺服通道的控制增量Δ()，从而获得各液压伺服通道的控制量为

()=(-1)+Δ()

(17)

3 仿真分析

升沉补偿平台的6个液压伺服系统相同，其参数也相同，系统的主要参数如表1所示。根据表1的相关参数，将每个液压伺服子系统的数学模型离散后得到()、()分别为

表1 液压系统主要参数

()=1-114+0258 7-0119 9+

0004 9-0001 7

()=0542 1+0816 9+0009 1+

0079 5+0006 8

经过多次仿真试验,确定所设计的每个广义预测控制器的控制参数为==5、=25、=0.35，同步误差补偿系数=0.5、=0.5，随机干扰噪声比例为0.01。设定的参考轨迹均为阶跃输入()，各液压伺服通道液压缸的输出为()，输出()与参考输入()之间的跟随误差为()。

在系统无干扰的情况下，基于相邻交叉耦合同步控制方式，采用广义预测控制算法，各个液压伺服系统响应速度快、控制输出()一致、跟随误差()能够快速稳定地趋向于0，如图3所示。采用PID控制，系统存在较大的超调现象，超调量为49%，如图4所示。

图3 基于GPC的相邻交叉耦合控制结果

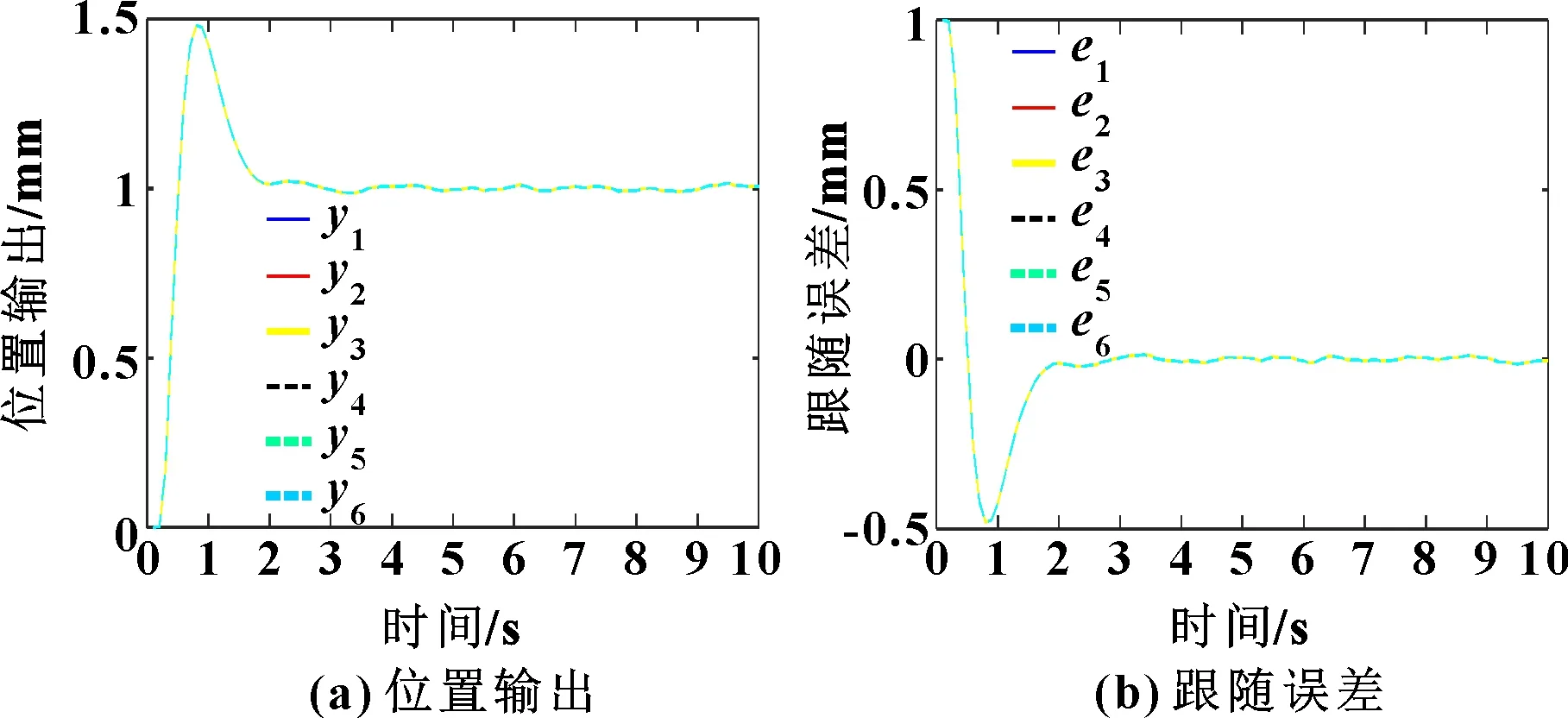
图4 基于PID的相邻交叉耦合控制结果

与相邻交叉耦合控制方式相比，采用基于广义预测控制的主从控制方式，以液压缸1的输出()作为其余液压伺服通道的输入，存在子液压缸位置输出()(=2,…,6)滞后的现象，导致子液压缸的跟随误差()(=2,…,6)一致增大，同步趋向于0的时间滞后，如图5所示。

图5 基于GPC的主从控制结果

在=3 s时，液压伺服通道1受到20%的阶跃负载扰动，同样地在=5 s时，液压伺服通道4受到20%的阶跃负载扰动。由图6可知：采用主从控制方式，主液压伺服通道受到扰动后，其输出()、跟随误差()增大，导致其子液压缸的输出()和跟随误差()一致增大。子液压缸4受到扰动，输出()增大，其跟随误差()增大，其余液压缸均不会受影响，延长了各液压缸的跟随误差一致趋向于0的时间，系统不具备较好的跟随性。

图6 受到扰动的主从GPC控制结果

由图7可知：采用相邻交叉耦合控制方式，液压缸1和液压缸4受到扰动，其输出()、()与参考输入()之间的跟随误差()、()增大，通过相邻交叉耦合作用，对同步误差进行反馈补偿，使相邻液压缸跟随误差()与()、()与()一致增大，其余液压缸也会有较小的变化，这样使得每个液压伺服系统的跟随误差变化保持一致。与基于PID的相邻交叉耦合控制相比，基于GPC的相邻交叉耦合控制在受到扰动后各液压缸的跟随误差较小，不存在较大的波动，能快速一致地趋向于0。

图7 有扰动时的跟踪误差

为实现对6个液压缸的同步控制，除了使跟随误差()趋向于0，还要考虑各个液压缸的同步误差，即各液压缸与其相邻2个液压缸之间的偏差之和()趋向于0。各液压缸的同步误差如图8所示。

图8 同步误差比较

由图8可知：主从控制方式下，在没有受到扰动的情况下，由于对同步误差的定义，子液压缸之间相互独立且输出滞后导致液压缸1、液压缸2和液压缸6的同步误差较大；受到扰动后，受扰通道与其相邻2个伺服通道的同步误差波动幅度较大，其余液压伺服通道对于扰动的影响不敏感，使各液压伺服系统的同步误差变化不能保持一致收敛于0。

由图8还可知：采用相邻交叉耦合控制，受到扰动后，液压缸1和液压缸4的同步误差()、()最大，通过将同步误差反馈到相邻液压伺服通道中，对相邻通道的控制量进行预测修正，使得相邻通道液压缸的同步误差，即()与()、()与()有所减小。由于同步补偿系数选取相同，相邻通道液压缸的同步误差变化相同，其余通道液压缸的同步误差也相应减小。而基于PID控制的相邻交叉耦合控制，受到扰动后各液压缸的同步误差均最大，波动周期较长，不能够快速地趋向于同步。

由图3—图8可知：采用所提控制策略，每个液压伺服系统在无干扰情况下，响应速度较快、位置输出一致，具有较好的跟随性，控制性能稳定；在有干扰的情况下，每个液压伺服系统的抗干扰能力较强、跟踪误差和同步误差较小、波动幅度较小，能够快速且一致地趋向于0。

4 结论

本文作者将广义预测控制与相邻交叉耦合控制相结合，使升沉补偿平台的6个独立的液压伺服子系统内部相互耦合、相互影响。在保证单个液压缸位置控制性能稳定的同时对6个液压缸进行相邻交叉耦合控制，使6个液压缸输出同步。结果表明：该系统响应速度快、不存在输出滞后现象，抗干扰能力较强，受到扰动后能够较快地恢复稳定，具有较高的位置控制精度和同步控制精度。