围绕“主问题” 感悟数学本质

谢玥

【摘要】本文以苏教版数学三年级下册“小数的初步认识”的教学实践为例，围绕主问题：任意两个相邻的整数之间会有新的数存在吗？从O～】以内的一位小数的探索，形成整体进入的牵引力;任意两个相邻的整数内一位小数的研究，形成认知结构的支撑力;生活中小数意义的发掘，形成课堂活动的凝聚力;关注发展，形成后续学习的推动力，这几个方面引领学生层层深入地探究，感悟数学本质。

【关键词】主问题 数学教学 牵引力 支撑力 凝聚力

“小数的意义”在苏教版教材的编排中安排在两个年级学习，三年级下册“小数的初步认识”和五年级上册“小数的意义”。在教学三年级下册第六单元“小数的初步认识”的前期，学生储备的知识基础有：（l）掌握了整数的认识知识结构。（2）已经接触了分数的初步认识。从整数到小数，是数域的一次扩展，学生的数概念从具有离散性的整数向具有稠密性的（非负）有理数发展。在学习整数的认识和分数的初步认识过程中，学生经历了从具体到半抽象的过程，对抽象的数字符号所表示的具体意义也有了一定的认识。所以，本课设计在数轴上把相邻的两个整数之间的距离平均细分并用小数表示的过程，让学生在经历小数形成的过程中了解小数与整数、小数与分数的内在关系。初步感悟小数的一些基本概念，小数的表示、十进制的计数单位、小数的精确作用，以及小数与数轴上点的对应关系等。为使知识系统化.本课以“主问题”为线索，围绕“主问题”，引领学生进行层层深入的数学研究。

一、情境激趣，生成主问题

出示情境：这两个同学身高分别是多少？比一比。学生大多数认为一样高。

小结：大多数同学认为他们的身高一样高，真的一样高吗？通过今灭的研究，我们可以进·步比出他们的高矮。

师：（估算）026÷4，43÷5。

生：第一题商是6余2，第二题商8余3。

师：（提出主问题）6～7之间、8～9之间还会有数存在吗？这样的任意两个相邻的整数之间会有新的数存在吗？

[思考]数学教学中的“主问题”，是引导学乍对教学内容进行研究的重要问题、中心问题或关键问题。这样的任意两个相邻的整数之间会有新的数存在吗？这个问题是在学生通过比身高和计算的过程中，发现所学知识不够表达，急需获得新知的需求状态而进入数学学习过程的。“主问题”既是对传统的课堂提问方式的改造和创新，也是对数学课堂活动方式的改造和创新。用“主问题”来形成课堂教学步骤的课，往往表现出一种“线索”之美，表现出“妙在这一间”的新颖创意。

二、围绕主问题，引领学生递进性探究

探究一：O-I以内一位小数的探索，形成整体进入的牵引力

第一层次：0～1米的一位小数。

师：首先从两个整数入手。选择最小的研究起。0～l之间有新的数存在吗？

师边说边画：把1米长的线段，平均分成10份，l份是多少呢？你能表示出来吗？

生1：1份表示1分米。

生2：1份也可以表示10厘米。

师：1分米、10厘米。还是用整数表示的，但是单位变了。如果不改变单位怎么表示？

师：是l米的1/10，就是1/10米。

还可以表示为0.1米。0.1米也表示把l米平均分成10份，表示这样的l份。介绍小数点，0.1的读法写法。

让学生说一说。如果取其中的2份，用分数怎么写，小数怎么写，又是什么意思呢？0.2米里面有几个0.1米？

学生相互说一说，然后在作业纸上把2分米改写成分数和小数。

2分米是1米的2/10，也就2/10米，还可以写成小数是（0.2）米。

取其中的三份呢？四份呢……用和它原来单位一样的分数、小数来表示。学生相互交流。

板书：1米的1/10，就是1/10米，还可以表示为0.1米。

第二层次：从1米平均分成10份，迁移到其他计量单位。

师：这条线段只可以表示1米平均分成10份吗？你可以把什么单位平均分成IO份？那么，每一份用同样的单位，分数、小数又是怎样表示呢？

生3：把进率为10的平均分，比如1分米、1厘米平均分成10份。

师：除了长度单位还有其他单位吗？

生4：“1元”平均分。

学生在作业纸上完成：这条线段还可以表示什么量？在1后面写上合适的单位。在数点上面写分数和下面写对应的小数。

资源生成：学生把进率为10的平均分，比如：1分米、1厘米、1元。也会有学生把进率不是10的平均分成10份，比如：1千克。

第三层次：聚类O～1之间的一位小数。

实物投影上把学生的作业纸放在一起。请同学仔细观察，这里除了单位不一样、长度不一样外，有什么相同的地方？

学生观察交流。

生l：分数、小数相同。

生2：都把1個量平均分成了10份。

生3：上面都是十分之几，下面都是零点几。

老师把大家找到的相同的地方在PPT呈现出来，大家可以更清楚地观察分数与小数之间有什么关系。

小结：都是把0～l看作一个整体，平均分成10份，十分之几就是零点几。

板书：像这样的0.1、0.2、0.3......它们小数点的右边只有一位，我们叫作一位小数。一位小数表示十分之几。边放PPT：缩短O～l，问：O～l之间有多少个一位小数？介绍0.1就是计数单位。0.9里面有几个0.1？ 10个0.1是多少？

同桌互说。认识计数单位就是0.1，感知一位小数的组成。

板书：10个0.1是1。

[思考]小数来自哪里，老师在这里及时引领了探究路径，把—个单位平均分成10份，十分之几就是零点几，让学生沿着研究路径从许多具体的单位l找到分数与小数间的对应关系，再通过寻找相同点的方法，从具象中归纳出抽象的知识内容。从知识内容的层面考虑，本片段：O～l以内一位小数的形成过程，在这里架构了整数分数小数知识之间的联系，这个板块的设计不仅仅停留在学生小数的来源的层面，更在于丰富学生的探究体验。在体验与感悟中获得的知识不是浮在表面的，是有生命力的，最易迁移，能为培养创新意识和实践能力提供有力的保障。

探究二：任意两个相邻的整数内一位小数的研究，形成认知结构的支撑力

第一层次：1～2之间的一位小数的形成。

过渡：

1.只有O～l之间有这样的一位小数吗？你能把l～2之间也这样平均分一分并写一写它们之间的小数吗？

教师呈现作业纸资源：

生1：0.1。

生2：1.1。

交流哪一种写法对？为什么？

生3：1.1对，1.1里面有1 1个0.1。

生4：1再加上1个0.1，合起来就是1.1。

生5：1～2之间，必须比1大，比2小。

老师表扬同学们的思维正确全面，并让学生继续写出1～2之间的所有一位小数。

师（引导）：1.1如果加上单位米，Il个0.1米，它就表示l.1米。如果加上分米呢就表示什么？你指一个一点几的小数加上单位，问同桌就是表示什么？同桌互相交流说一说。

师：1.9里面有几个0.1 ？再加1个0.1呢？

生：1.9里面有19个0.1。再加上1个0.1.就是20个0.1，20个0.1就是2。

第二层次：任意两个整数之间的一位小数

师：2～3之间会有哪些一位小数？3～4呢？刚才除法估算说商在6～7之间，商在8～9之间，可能会是什么数呢？左右同学互选一个说给同桌听。1ooo～1001之间有这样的一位小数吗？说得完吗？

学生之间相互交流。

师：同学们说也说不完，我们用一个箭头来表示还有很多很多。这样的一条数线就是：数轴。数轴上每个相应的细点，都有一个数存在，无限多。PPT演示数轴的产生：

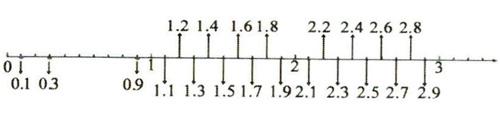
师：刚才讲了很多一位小数，那每相邻的两个整数之间有几个一位小数？

生：每相邻两个整数之间有9个一位小数。

板书：把黑板上的数线完成生成数轴。

[思考]只有O～l之间有这样的一位小数吗？你能把1～2之间也这样平均分一分并写一写它们之间的小数吗？这是教师创没的吏有意义的问题情境，让学生运用上一层次的研究方法来突破教学点，给学生更多的实践和思考空间，1～2之间的第1小格是写1.1还是0.1呢？学生在学习小数时的潜藏问题，通过学生之问的探究和碰撞而解決，学生在思辨中明理而不是老师乏味地告知。同样，这个片段的第二层次，通过一连串到位的设问点拨，引起学生的深层思考后巧妙地提出：说得完吗？由说也说不完产生了怎样表达的学习需求，数轴自然而然地生成。在这样的实践活动和思维活动中，学生不断经历、体验和探索，在理解和掌握知识技能的同时，获得了精神层次的享受，是本课最出彩之处。

探究三：生活中小数意义的挖掘，形成课堂活动的凝聚力

第一层次：感受小数的精确性。

课前两个同学的身高都是132厘米多一些，学剑现在有没有好办法让大家准确知道他们的身高是多少？在学生发言的基础上电脑演示。132厘米到133厘米之间平均分成10份。

读一读两个同学的身高，并比一比。

小结：和原来的大约132厘米比较，显得精确了。

第二层次：读读说说生活中的小数表示什么意思。

PPT演示生活中的小数（图略）。在生活中你见到过这样的小数吗？说说什么意思.并观察小数部分不同点。

生：39.4千克比39千克重一些，比40千克轻一些。

小结：一位小数的意义。帮助学生归纳一下读法。整数部分按以前的读法读，小数部分读数位上的数字。

板书：各部分名称及书写法。

第三层次：看图填上合适的分数或小数

哪幅图可以表示0.3？

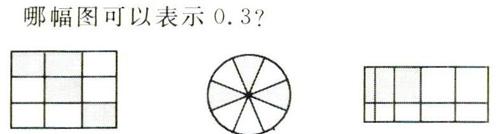
[思考]学生的数学学习不应是单纯的知识传授，它源于生活、富于生活、用了生活。越贴近学生生活的内容越容易引起学生共鸣。通过比身高这个熟悉的生活情境及复习了一位小数的认读又感悟了小数的精确性。在认读有小数的许多生活场景的过程中，体会小数在现实生活中的意义，并且发现除了一位小数，现实生活中还碰到过两位小数，等等。本环节学生经历了从理性到生活化的应用，再问到理性的思考。学生们积极投入到学习中，对原本已有的直接经验在头脑中进行了理性加工，获得了数学发展和处理问题的能力。

探究四：关注发展，形成后续学习的推动力

今天我们学习了一位小数，知道一位小数的产生、意义及读写方法。刚才同学们在读小数的时候，就知道还有两位小数，它又是怎样产生的呢？还有三位小数呢？想一想，回顾一位小数研究的过程，方法能不能用到两位小数的研究上？

[思考]克莱因认为：“数学是人类最高的智力成就，也是人类心灵最独特的创作。”我们教给学生知识的同时，也应使用相应的知识去让学生感受数学的文化魅力，得到精神上的熏陶。整节课，学生在“主问题”的引领下，运用了迁移、类推、抽象等方法，建立了小数的产生及其意义的模型。浓浓的数学味，没有使学生感到小数概念学习的枯燥，反而随着整节课的层层推进兴趣盎然。这里虽然用寥寥几句话总结了全课，但是通过回顾学习的方法结构，为后续知识的拓展埋下了伏笔。

【参考文献】

[1]章晨，小学数学课堂主问题式的教学探索[J].小学科学（教师版），2014（7）.

[2]郁兴林.以数学问题的解决为主线，巧妙推进循环教学[J].陕西教育（理论版）.2016（12）.

[3]姜纪华.以问题为主线的数学思维教学[J].数学大世界（下旬）.2017（2）.

[4]漆英，“问题”是数学的“主线”[J].四川教育，2017（12）.