C2B个性化定制平台欺诈定制行为治理研究

王 潇 杜明月

（重庆工商大学工商管理学院 重庆 400067）

引言与文献综述

随着居民消费结构不断升级，以消费者为主导的C2B个性化定制平台模式逐渐成为平台模式中的核心业务。据智研咨询发布的《2020-2026年中国综合电商行业发展动态及市场规模预测报告》显示：收入提高驱使消费者对商品品质提出更高要求，82.2%的中等收入人群已将产品质量作为消费时的首要关注因素，C2B个性化定制平台模式有望快速发展。然而，由于大规模生产与个性化定制的不兼容，以及标准化生产所需要的需求稳定条件与消费者需求动态性事实之间的矛盾，众多制造企业要实现C2B个性化定制平台运营举步维艰。

在此背景下，部分资金不足、个性化定制技术难以突破的企业开始选择生产欺诈定制产品，以谋求更高利润。欺诈定制指企业声称C2B个性化定制，却仅为消费者提供以生产者主导的大规模简单定制产品的现象。囿于此类欺诈定制产品仅是名义上的个性化定制产品，不仅不能满足消费者真实需求，还难以得到相应退货补偿，对广大消费者造成了极大损失。因此，如何有效治理C2B个性化定制平台企业欺诈定制行为，真正满足消费者升级变化的个性化定制需求正成为亟待解决的问题。

分析文献发现，已有部分学者运用博弈论方法对电商平台信用监管问题展开研究，其中政府作为第三方监管机构的介入引起了学术界广泛关注。曹裕等建立一对多的政府与B2C电商企业对称博弈模型，分析得出政府加大对企业的检查频率、降低企业自律成本有利于规范企业自身行为；南小可等针对B2C电子商务模式中的加盟店信任问题，构建了一种信任信息共享机制，验证了政府作为第三方信用监管机构对信任信息共享的积极作用；伍洛熠等基于完全信息静态博弈模型与重复博弈模型，提出通过政府监管提高卖家诚信概率和买家购买概率是确保C2C电商诚信行为的主要因素。然而，囿于政府机构的信息劣势以及监管执行的高昂成本，仅有政府监管通常难以起到预期效果。Swarbrooke和Horner从心理学、经济学的角度研究消费者行为，发现作为产品需求方的消费者行为会间接对企业价值产生影响；Balan等基于Solomon的观点进一步提出，C2B个性化定制平台运营模式下消费者评价有助于企业的行为规范。上述研究揭示了政府和消费者对电子商务平台失信行为治理的积极意义，为本研究奠定了坚实基础，但仍存在以下不足：C2B个性化定制平台作为一种新兴电商模式，既有文献较少研究政府监管对规范C2B个性化定制平台欺诈定制行为的正向影响；罕有文献讨论消费者对C2B个性化定制平台欺诈定制行为的影响；尚无文献将政府、消费者、C2B个性化定制平台纳入统一框架，研究政府和消费者对C2B个性化定制平台欺诈定制行为的抑制作用。

综上，本文将应用演化博弈研究方法，将政府、C2B个性化定制平台和消费者三者纳入统一研究框架，研究C2B个性化定制平台欺诈定制行为治理。相比现有研究，本文创新之处体现在以下两个方面：首先，与以往集中研究B2C电商平台、B2B电商平台以及C2C电商平台信用监管机制的文献不同，本文聚焦研究C2B个性化定制平台的欺诈定制行为治理机制；其次，与以往将政府纳入博弈监管主体的文献不同，本文引入政府与消费者共同参与博弈，构建出政府-C2B个性化定制平台-消费者三方演化博弈模型。

问题描述和符号说明

消费者个性化需求的升级变化，驱动企业面向C2B个性化定制平台运营模式变革。然而，C2B个性化定制平台运营模式需要企业耗费高昂的创新与迭代试错成本，因此部分尚不具备C2B个性化定制平台运营基础的企业选择欺诈定制以谋求更高利润，而由于产品7天无理由退货的电商条例并不适用于个性化定制产品，消费者将难以通过退货弥补损失，进一步助长C2B个性化定制平台的欺诈定制行为。由此可见，C2B个性化定制平台欺诈定制行为一方面会严重损害消费者的利益，另一方面也会使部分消费者失去对C2B对个性化定制行业的信任。基于上述描述，本文引入政府、消费者构建出“政府-C2B个性化定制平台-消费者”的信用监管机制模型。

假设1：政府监管部门为参与人1，C2B个性化定制平台为参与人2，消费者为参与人3，三方均是有限理性的参与主体，策略选择随时间逐渐演化稳定于最优策略。

假设2：政府监管部门的策略空间α=（α，α）=（严格监管，宽松监管），并以x的概率选择α，以（1-x）的概率选择α，x ∈[0，1]；C2B个性化定制平台的策略空间为λ=（λ，λ）（诚信定制，欺诈定制），其选择λ的概率为y，选择λ的概率为（1-y），y ∈[0，1]；消费者的策略空间γ=（γ，γ）=（给出差评，不做差评），并以z的概率选择γ，以（1-z）的概率选择γ，z∈[0，1]。

假设3：政府税率为r，严格监管成本为C，当政府严格监管时，政府会产生K的额外收益，并对生产欺诈定制产品的C2B个性化定制平台进行F的惩罚。

假设4：C2B个性化定制平台诚信定制时的收入为R，欺诈定制时的收入为R，其中C2B个性化定制平台为欺诈定制所付出的投机成本为C，R＞R+C。

假设5：消费者若收到C2B个性化定制平台诚信定制的产品，则获得效用U，反之若收到欺诈定制产品则效用为U；此外，消费者给出差评时的流失率为β，流失消费者会转换到其他平台，转换成本为L。

模型分析

根据以上假设，列出政府、消费者与平台的混合策略博弈矩阵，如表1所示。

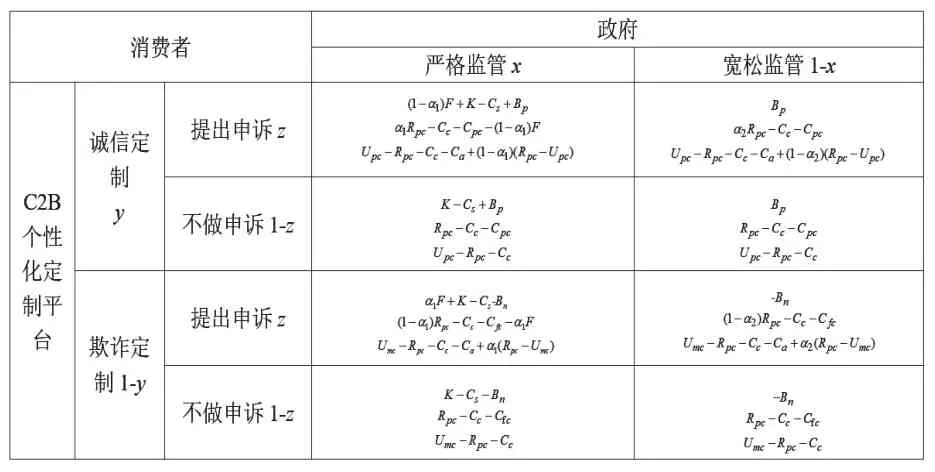
表1 政府、消费者与平台的混合策略博弈矩阵

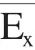
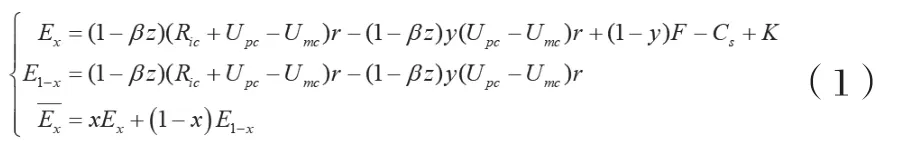
政府策略选择的复制动态方程为：

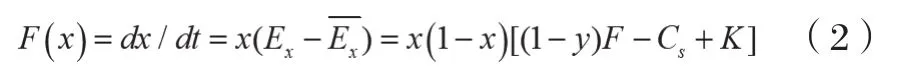
x的一阶导数和设定的G（y）分别为：

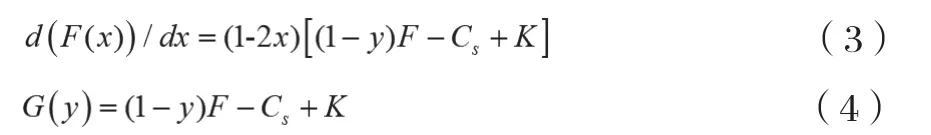
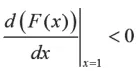
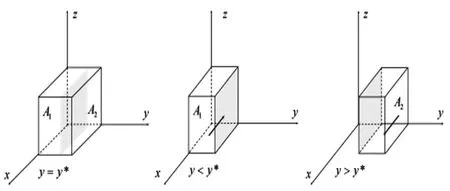
图1 政府策略演化相位图

图1表明，政府严格监管的概率为A的体积V，政府宽松监管的概率为A的体积为V，计算得：

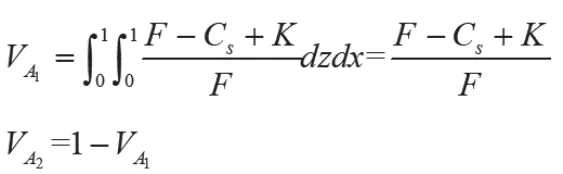
推论1：政府严格监管的概率与政府对欺诈定制C2B个性化定制平台的惩罚F、政府监管的额外收益K正相关，与政府严格监管成本C负相关。

证明：根据政府严格监管的概率V的表达式，求各要素的一阶偏导数得： V/F＞0，V/K＞0，V/C＞0。因此，F、K的增加或C的减少，均可提升政府严格监管的概率。

推论1表明：一方面，政府对欺诈定制C2B个性化定制平台惩罚力度和政府严格监管额外收益的提升，会增加政府严格监管的概率；另一方面，政府严格监管的成本会抑制政府严格监管的决策制定。

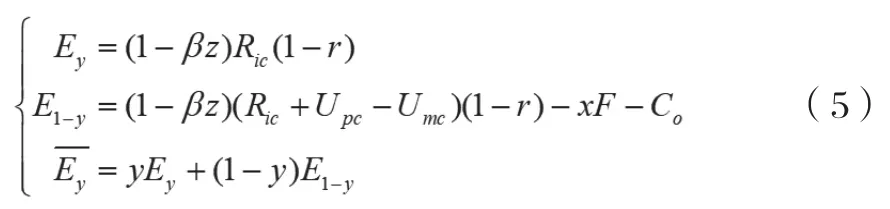
C2B个性化定制平台策略选择的复制动态方程为：

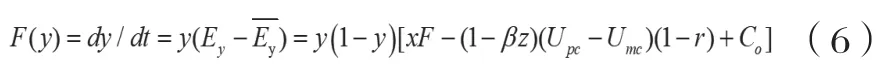
y的一阶导数和设定的J（z） 分别为：

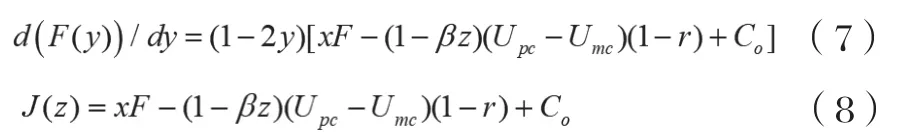
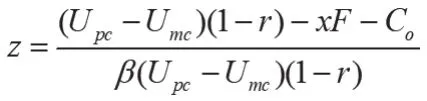
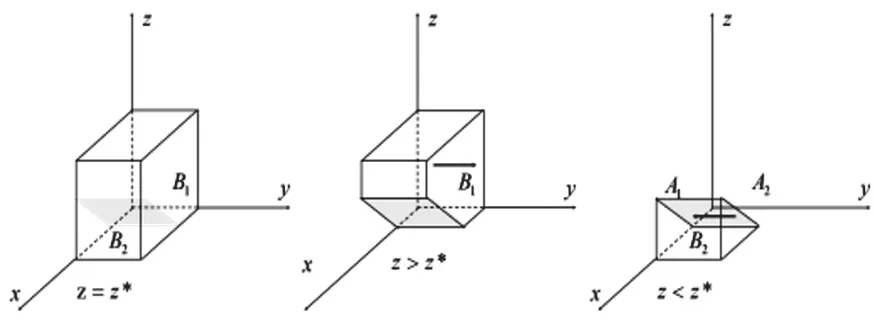
图2 C2B个性化定制平台策略演化相位图

图2表明，C2B个性化定制平台诚信定制的概率为B的体积V，欺诈定制的概率为B的体积V，计算得：

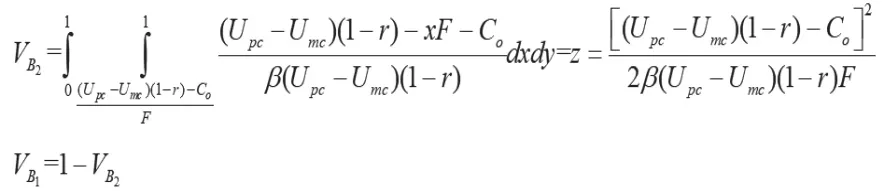
推论2：一方面，C2B个性化定制平台诚信定制的概率与政府对欺诈定制的C2B个性化定制平台的惩罚F和消费者流失率β负相关；另一方面，当C2B个性化定制平台欺诈定制所剥夺的税后消费者收益大于欺诈定制所耗费的投机成本时，C2B个性化定制平台诚信定制的概率与欺诈定制所剥夺的消费者收益（U-U）、税收率r和欺诈定制所耗费的额外成本C负相关，反之亦反。

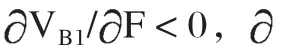
推论2表明：一方面，消费者流失率提升或增强对C2B个性化定制平台欺诈定制行为的惩罚力度，能够有效遏制C2B个性化定制平台的欺诈定制行为；另一方面，提升C2B个性化定制平台欺诈定制所耗费的投机成本、增加政府税收以及降低C2B个性化定制平台欺诈定制所能从消费者处剥夺的收益，对于治理C2B个性化定制平台欺诈定制行为并不总是有效的，具体体现在当C2B个性化定制平台欺诈定制所剥夺的税后消费者收益已经大于欺诈定制所耗费的额外成本时，即使降低该种剥夺收益和提升欺诈定制额外成本，C2B个性化定制平台仍然会选择欺诈定制，此时政府因税收率太低而缺乏监管效力。

3.消费者策略稳定性分析。消费者给出差评的期望收益E、不做差评的期望收益E以及平均期望收益Ez分别为：

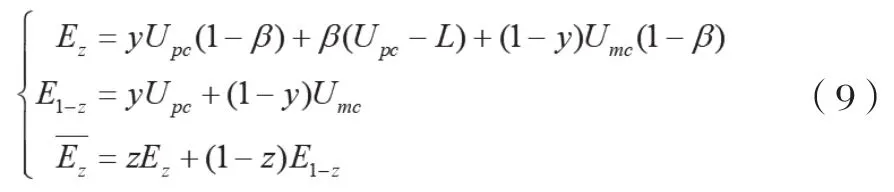
消费者策略选择的复制动态方程为：

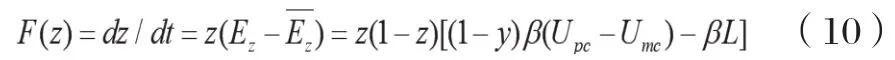
z的一阶导数和设定的H（y）分别为：

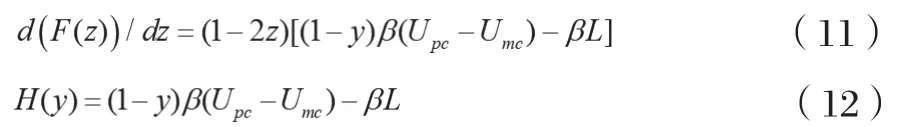
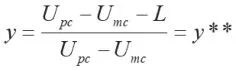
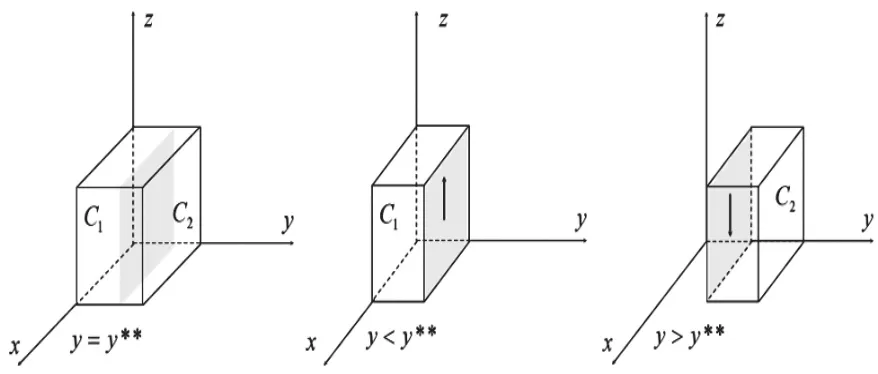
图3 消费者策略演化相位图

图3表明，消费者给出差评的概率C为体积V，不做差评的概率C为V的体积，计算得：

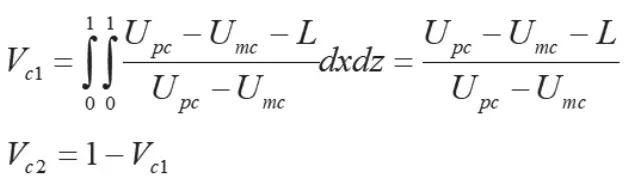
推论3：消费者给出差评的概率z对消费者获得个性化定制产品与大规模定制产品效用之差（U-U）负相关，与转换到其他平台的成本L正相关。

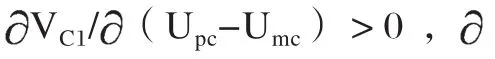
推论3表明：当个性化定制产品对于消费者效用较高时，消费者会更倾向于维护自身权益，给出差评；此外，消费者提出申诉后转换到其他平台的成本是阻碍消费者给出差评并进一步转换到其他平台的重要因素之一。

4.三方演化博弈系统均衡点稳定性分析。由F（x）=0，F（y）=0，F（z）=0可得系统均衡点E（0，0，0），E（1，0，0），E（0，1，0），E（0，0，1），E（1，1，0），E（1，0，1），E（0，1，1），E（1，1，1）（因混合策略中不存在演化稳定点，故将其排除，仅讨论纯策略系统均衡点的演化情况）。三方演化博弈系统的Jacobian矩阵为：

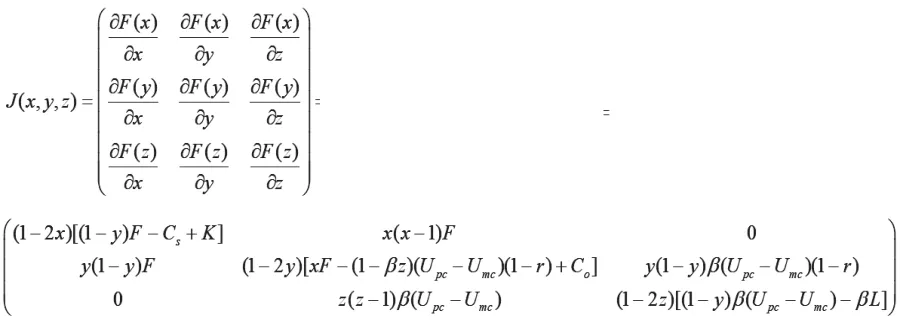
利用李雅普诺夫（Lyapunov）间接法：雅克比矩阵的所有特征值均具有负实部，则均衡点为渐进稳定点；雅克比矩阵的特征值至少有一个具有正实部，则均衡点为不稳定点；雅克比矩阵除具有实部为零的特征值外，其余特征值都具有负实部，则均衡点处于临界状态，稳定性不能由特征值符号确定。分析各均衡点的稳定性，如表2所示。

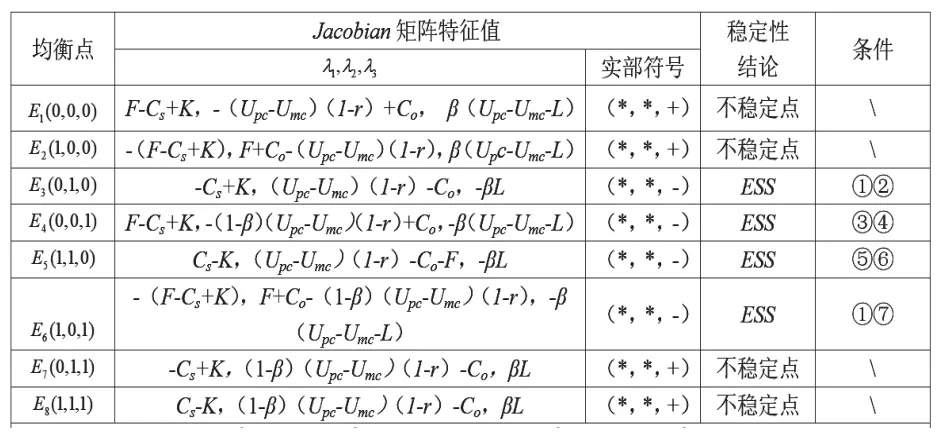
表2 均衡点稳定性分析

推论4：当-C+K＜0且（U-U）（1-r）-C＜0时，复制动态方程存在稳定点E（0，1，0）。

证明：根据表2，此时满足条件①②，雅克比矩阵实部特征值均为负，故为E（0，1，0） 稳定点。

推论4表明：当政府严格监管成本小于严格监管所获得的额外收益，且C2B个性化定制平台通过欺诈定制对消费者剥削的效用小于欺诈定制所耗费的额外成本时，三方策略组合会稳定于（宽松监管，诚信定制，不做差评），侧面验证了推论1、推论2和推论3的部分结论。

推论5：当C-K＜0且（U-U）（1-r）-C-F＜0时，复制动态方程存在稳定点E（1，1，0）。

证明：根据表2，此时满足条件⑤⑥，雅克比矩阵实部特征值均为负，故E（1，1，0） 为稳定点。

推论5表明：当政府严格监管成本小于严格监管所获得的额外收益，且政府通过罚款和税收使C2B个性化定制平台欺诈定制收益小于欺诈定制成本时，三方策略组合会逐渐稳定于（严格监管，诚信定制，不做差评），侧面验证了推论1、推论2和推论3的部分结论。

仿真分析

为验证上述推论的科学性与准确性，本小节将利用数字仿真进行检验。根据谢康等采用的方法，参数取值范围主要有两方面依据：一是真实数据可获取性，二是等式平衡原则。因此，本文以尚品宅配为例，参照等式均衡原则对仿真数据进行相应调整（数值不代表实际金额，表示各参数之间的相对大小），给出以下两组数值：数组1：U=1，U=0.8，β=0.1，F=1，L=0.1，C=0.1，K=0.08，r=0.3，C=0.15；数组2：U=1，U=0.8，β=0.1，F=1，L=0.1，C=0.1，K=0.12，r=0.3，C=0.1。由于演化稳定均衡点的结果能够侧面验证推论1、推论2和推论3的结论，因此为简化仿真过程，本文主要基于数组1、数组2验证政府、平台和消费者三方演化策略稳定均衡点。

验证当数组1满足推论4中的条件时，演化均衡点E（0，1，0），将数组1从不同初始策略组合出发随时间演化500次，结果如图4所示；验证当数组2满足推论5中的条件时，演化均衡点E（1，1，0），将数组2从不同初始策略组合出发随时间演化500次，结果如图5所示。由图4可知，在满足推论4中的条件时，仿真结果E（0，1，0）为唯一均衡点，与推论4结果一致。图5表明，在满足推论5中的条件时，系统也仅存在唯一演化稳定点E（1，1，0），与推论5结果一致。

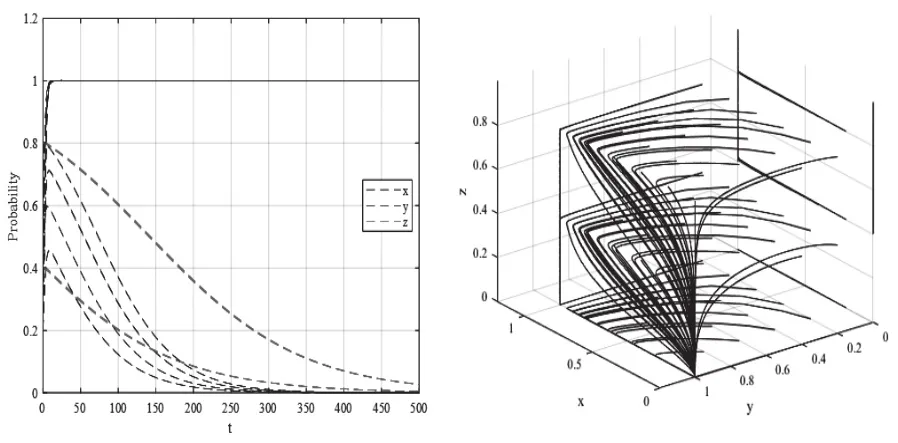
图4 数组1的演化500次结果

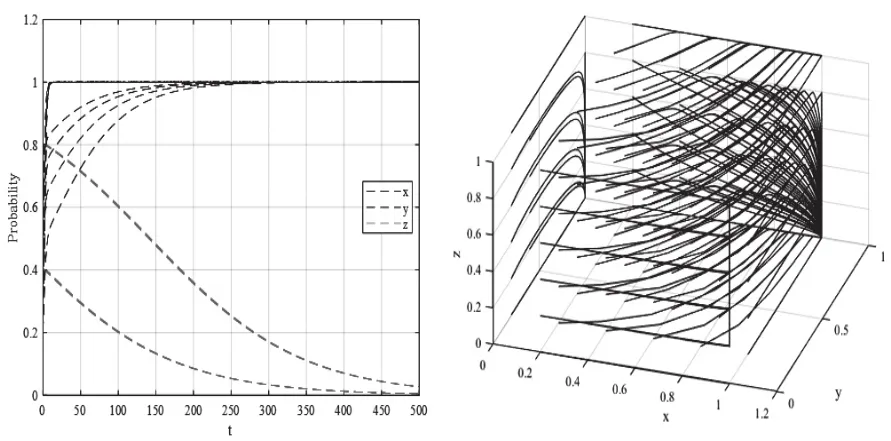
图5 数组2的演化500次结果