基于滑模变结构的Vienna 整流器控制研究

薛 彪，党超亮

（1.陇东学院电气工程学院，庆阳 745000；2.西安理工大学电气工程学院，西安 710048）

随着通信技术与计算机技术的快速发展，构建安全、可靠、高效的高性能大数据中心供电系统业已引起了世界范围内的普遍关注[1-3]。与传统交流不间断电源UPS（uninterruptible power supply）供电电源结构相比，“AC+DC”两级式互联高压直流供电系统显示出了高可靠性、高密度与高效率的优势。与低压48 V 供电结构相比，240 V 高压直流供电电源系统可有效减少线路损耗、节省机房建设成本。文献[4]对5 种不同整流拓扑分别从功率密度、开关器件等方面综合整合，表明三电平单向Vienna 型混合整流器效率最高、半导体芯片面积最小、功率密度最大、综合性能最优，故其选用三电平Vienna整流器作为前级PFC 模块单元。前级PFC 整流模块在两级级联系统中扮演着重要角色，其性能直接影响到整机可靠性运行。为有效提升整机功率密度，很多学者相继提出了解决方案。

文献[5]提出了引入中点电位平衡修正机制的Vienna 滞环控制，然而电流内环采用滞环控制时，控制性能受给定环宽的影响较大，开关频率不固定，也给网侧滤波电感的设计带来困难；文献[6]提出了基于单周期控制的三电平Vienna 整流器控制策略，通过输入电流采样注入三次谐波抑制中点电位波动，然而并未给出当中点电位不平衡时的相关实验验证，同时其推导过程过于繁琐。文献[7]提出了三电平Vienna 整流器有限集模型预测控制策略，针对中点电位波动与网侧电流性能进行了研究。

除上述传统控制算法外，大量的新型高性能非线性算法在并网变换器中也得到了广泛应用，如滑模变控制[8]、无源控制[9]、模型预测[10]等等。其中滑模控制SMC（sliding mode control）算法作为一种高性能的非线性控制算法，可在有效抑制周期性干扰的同时保证较高的并网功率因数和正弦度，因此在并网变换器中获得了广泛关注[11-12]。文献[8]提出了基于SMC-DPC 的Vienna 整流器控制方法，有效提高了并网电流的动态响应速度，然而直接功率控制方案计算繁琐且并未给出中点电位波动抑制办法；文献[13]将无源算法与滑模变结构相结合，并应用在三电平Vienna 整流器中，整机性能得到较大改善，然而内环控制系统复杂，且并未给出中点电位控制方法，有一定局限性。

综上所述，关于Vienna 整流器的相关控制方案已取得了一定成果，然而尚缺乏有关Vienna 整流器双闭环滑模控制的相关研究。本文在前人工作的基础上，提出并采用基于双闭环滑模变结构的三相Vienna 整流器控制方案，分别给出电压外环与电流内环SMC 理论设计方法，并进一步采用改进型的指数趋近律有效减小抖振影响。最后，进一步给出中点电位直流波动抑制方案，有效避免传统控制策略中并网电流质量强依赖控制参数、低鲁棒的缺陷。最后，基于完整的仿真与实验平台进行必要的验证分析，为三相Vienna 整流器提供一种全面的新型SMC 控制方法。

1 三相Boost 型Vienna 整流器电路拓扑及数学模型

本文采用的三相三电平Vienna 整流器电路拓扑如图1 所示[14]。usx（x=a，b，c）为三相交流电网电压；ix（x=a，b，c）为网侧电流；L 为交流侧升压电感；R 为电感寄生电阻；Qx为由2 个反向串联构成的双向电流开关；直流侧输出电容由C1与C2构成；Dxp与Dxn为不控整流二极管；iop与ion为直流侧输出电流源；RL1=RL2=0.5RL为直流侧纯阻性负载；udc1、udc2为正、负母线电压；u0为直流输出电压。

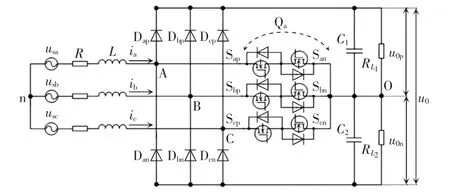
图1 三电平Vienna 整流器电路拓扑Fig.1 Circuit topology of three-phase Vienna rectifier

为简化分析，首先做如下假设：

（1）电路运行在稳定状态，且开关频率远高于电网频率，网侧电流运行于连续模式；

（2）直流侧电容足够大，稳态时直流电压稳定无纹波，中点电位平衡且三相严格对称。

根据图1 列写Vienna 整流电路回路方程为

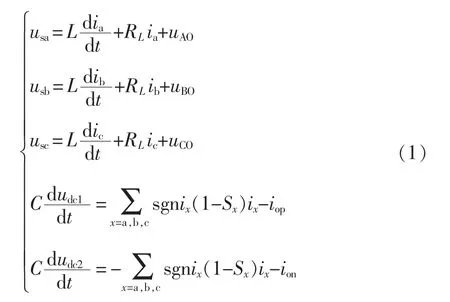
式中：uAO、uBO、uCO分别为整流桥输入电压；Sx为开关函数。定义开关函数Sx为

符号函数sgnix为

Vienna 整流器作为一种强制换流的能量单向流动的整流器，整流桥输入电压不仅取决于开关管的通断状态，也与电流极性相关，输入电压表达式为

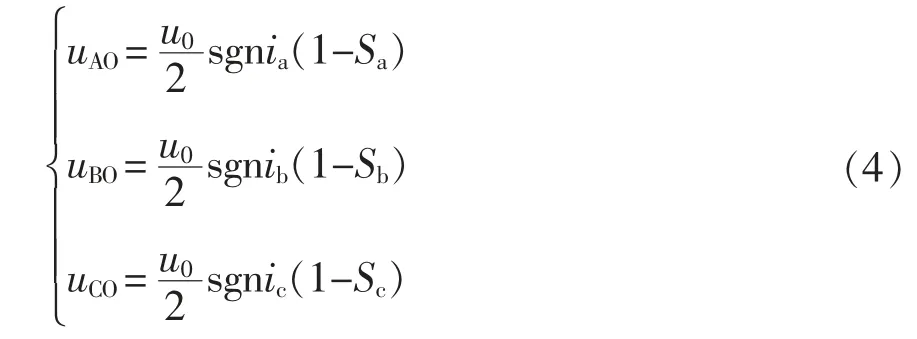
为消除电流极性影响，从开关平均周期建模本质出发，假定开关管在平均开关周期Ts内导通时间为Tx，定义占空比dx表达式为

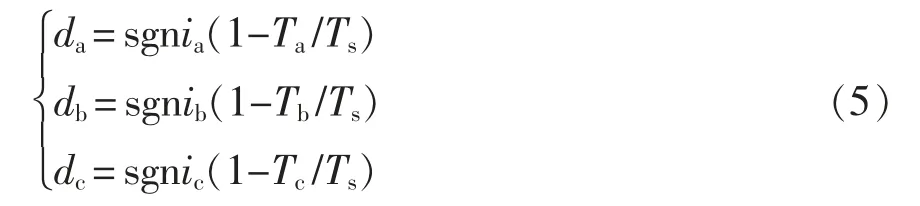
将式（5）代入式（1）可得

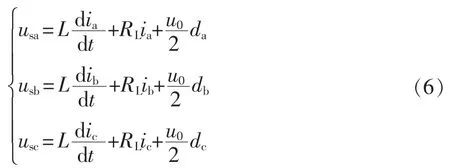
在此引入d-q 坐标变换矩阵，式（6）可列写为

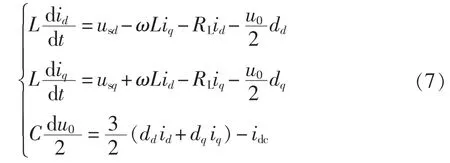
式中：ω 为角频率；下标d、q 表示dq 坐标系下对应的各参数。

2 滑模系统结构设计

2.1 控制系统结构设计

滑模变结构区别于传统控制策略的优势在于其“结构”并不是固定不变的，而是随着系统状态的改变而不断变化，同时具有不需要系统在线辨识、响应速度快、对系统参数变化不灵敏、实现方法简单、对外界扰动不敏感等优点，因此对阶数较高的非线性变结构系统有很好的适应性[15]。基于上述考虑，在此采用基于滑模控制算法的电流环路设计方案，本文设计的基于滑模变结构的三相Vienna 双闭环型并网逆变器控制结构如图2 所示。

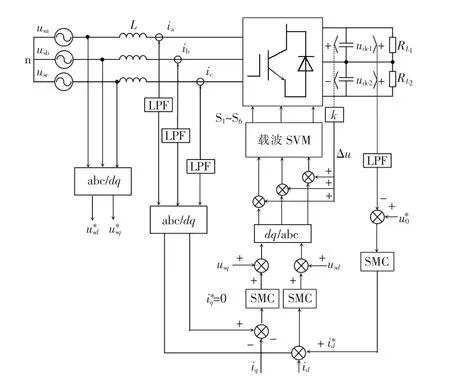
图2 本文所提SMC 系统结构Fig.2 Structure of the proposed SMC control system

为有效抑制电网电压波动的影响，在此引入了网侧电压前馈控制，经过锁相环保证系统单位功率因数。然而，与传统控制不同，电流环作为并网逆变器核心，其控制性能直接影响并网功率因数。而当采用传统控制算法时，并网电流性能对于控制器参数依赖性较强，且抗扰动性差，因此本文采用基于滑模变结构的双闭环控制方案。

对于三电平Vienna 整流器而言，虽然可以通过参考矢量修正实现三电平空间矢量脉宽调制SVPWM（space vector pulse width modulation）到两电平空间矢量调制SVM（space vector modulation）的简化，然而传统SVPWM 仍须进行大量计算。为避免控制程序繁琐同时保持常规SVPWM 优势，本文采用等效载波-SVM 方案。根据三相三电平Vienna整流系统工作原理的简要分析，给出载波-SVM 实现方案，假设Uk（k=a，b，c）为ud、uq信号经dq/abc 坐标变换的三相调制信号，Mk为调制信号，定义为

根据文献[16-17]分析可列写载波SVM 信号为

2.2 电压外环SMC 系统设计

与传统双闭环PI 控制结构相似，本文设计采用基于滑模变结构的双闭环系统，可分为电压外环滑模控制器与电流内环滑模控制器。其中有功电流分量id由电压外环生成，因此按照串级系统设计思路，分别给出电压外环与电流iq设计方案。常规的滑模变结构设计主要分为滑模面、控制律和趋近率的设计等[17-18]，其中控制系统的动态性能主要取决于趋近率，而滑模控制律主要是迫使系统状态轨迹平稳滑动面。首先根据系统功率平衡，可以列写电压离散方程为

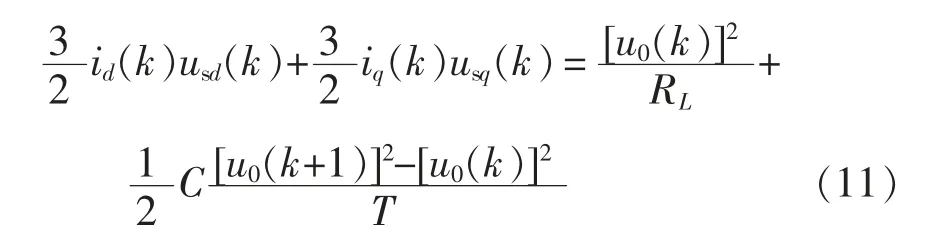
式中，T 为采样频率。对于三相平衡系统，可得usq=0。根据式（11）可列写直流输出电压方程为

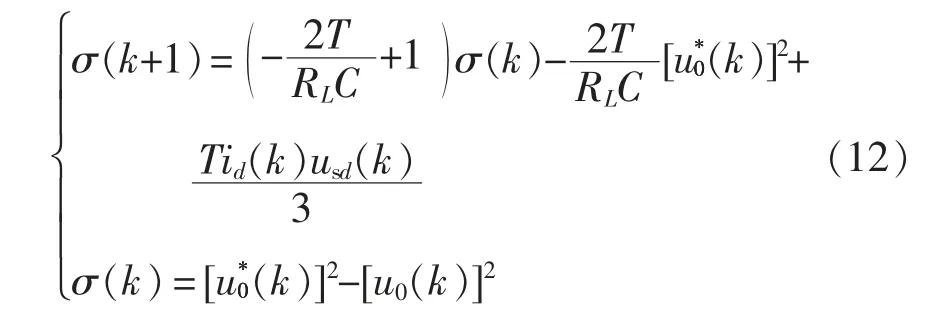
一般情况，滑模变结构系统设计时选择滑模面为σ（k）=cx（k），其中c 为常数且恒大于0，u0（k）为直流侧电压采样值。实际系统中，由于惯性、时间延迟等因素，当状态轨迹到达滑模面后，运动点在滑模面两侧来回穿越，不可避免地引起“抖振”，一方面易导致不稳定现象，另一方面会增大系统消耗，同时还影响控制精度[19]。为有效消除抖振并提升系统趋近速度，本文选取指数趋近率，其表达式[19-20]为

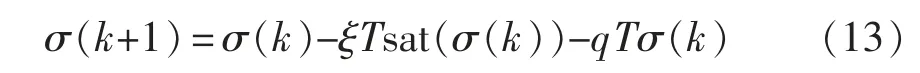
式中：0＜qT＜1；ξT>0；符号函数sat（σ（k））为饱和函数，定义为

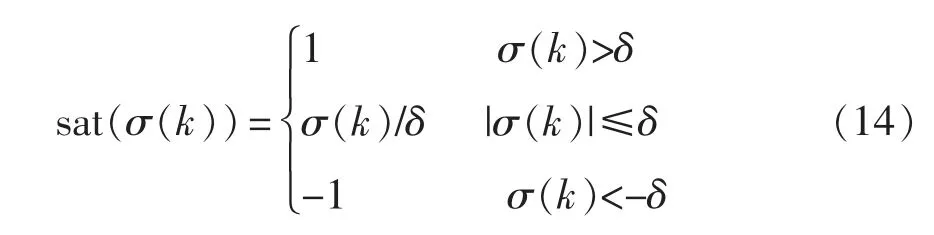
式中，δ 为边界层，δ>0，δβ=1 且δ>ξT/（1-qT）。

假定三相电网电压严格对称，则当系统到达稳态时，usq=0，iq=0，du0/dt=0，此时有σ（k）=0，则代入上述公式分析可得离散滑模变结构控制器输出量u（k）表达式为

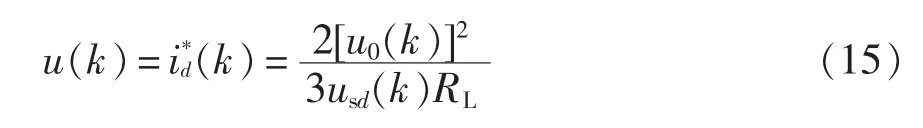
当系统到达滑模面时，有σ（k+1）=σ（k）=0，由此可得离散滑模变结构控制器等效输出控制量uek（k）为

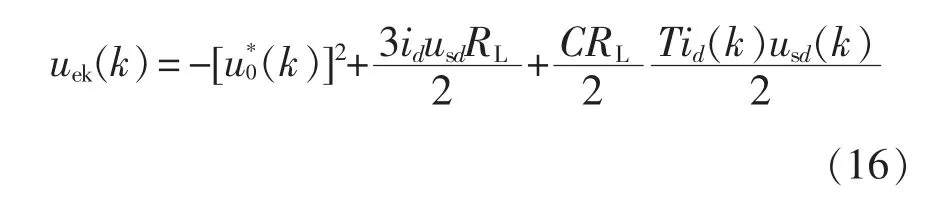
2.3 电流内环SMC 系统设计

本文提出的电流内环滑模变控制结构如图3所示。其中电流内环控制中考虑了中点电位直流波动，目前针对中点平衡常规的有小矢量修正、直流偏置注入或零序电压注入等几种方案[21-22]，然而均过于复杂且控制效果不佳。基于此，本文给出一种简单有效的控制方案。正负母线电压做差后经过准比例环节后，生成零序分量Δu，Δu 与内环环路输出电压叠加后经载波SVM 环节输出最终的开关控制信号。其中，中点电位调节系数k 与直流侧输出电容和网侧电流相关，其取值决定于

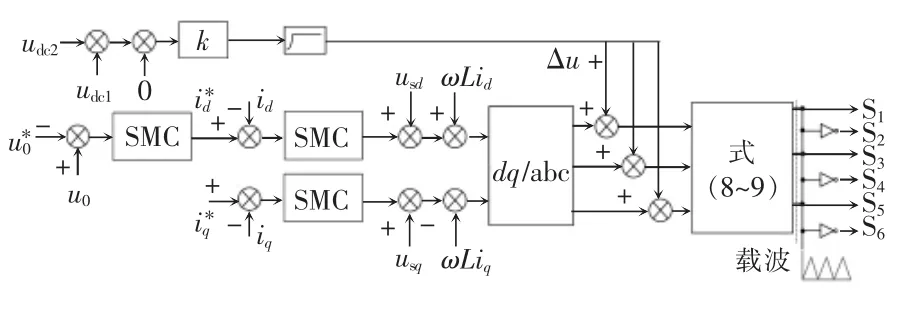
图3 电流内环SMC 控制结构Fig.3 Structure of current inner loop under SMC control

式中，Im为电流有效值。

实际系统中为避免均压环路冲击，同时考虑到中点电压的3 倍频波动，在此引入二阶低通滤波环节，低通滤波截止频率取为100 Hz。

滑模变结构控制系统的动态性能主要取决于趋近率，而滑模控制律主要实现系统状态轨迹平稳趋近滑动面。在此选取同步坐标下网侧输出电流为控制量，定义电流误差函数分别为

式中，C=[c1c2]T，c1与c2均为常值。

目前常用的趋近律法主要包括等速趋近率、指数趋近率与幂次趋近率等。其中等速型趋近速度取决于趋近系数，趋近面附近存在抖振现象；为降低抖振指数型引入了指数与等速趋近，然而并不能完全消除抖振现象；在此基础上，有学者进一步提出了幂次型趋近率，虽能保证系统平滑过渡，然而趋近过程缓慢。为有效消除抖振并提升系统趋近速度，本文采用一种新型的趋近率，其表达式[17]为

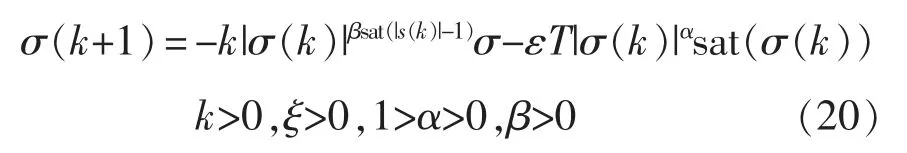
可以看到，对于三相LCL 型逆变系统，当滑模切换函数|s|>1 时，等效为幂次型趋近率，|s|≤1 时，趋近速率显著高于指数型，同时当切近面时速度渐缓，可有效降低高频抖振。

假设系统稳态运行，则将式（4）与式（6）代入式（7）可得

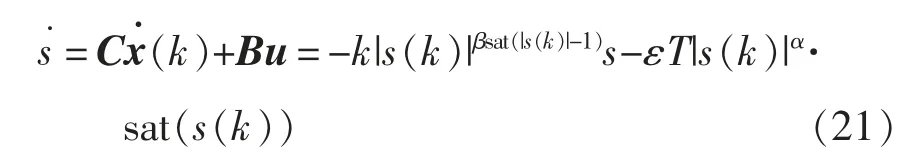
根据式（4）与式（6）、式（7）分析可得离散滑模变结构控制器输出控制量u（k）表达式为

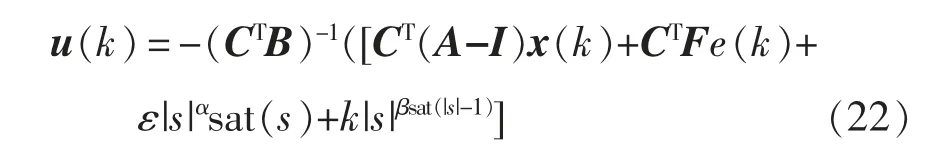
当工作于滑模面时，有s（k+1）=s（k），可得离散滑模变结构控制器等效输出控制量u（k）为

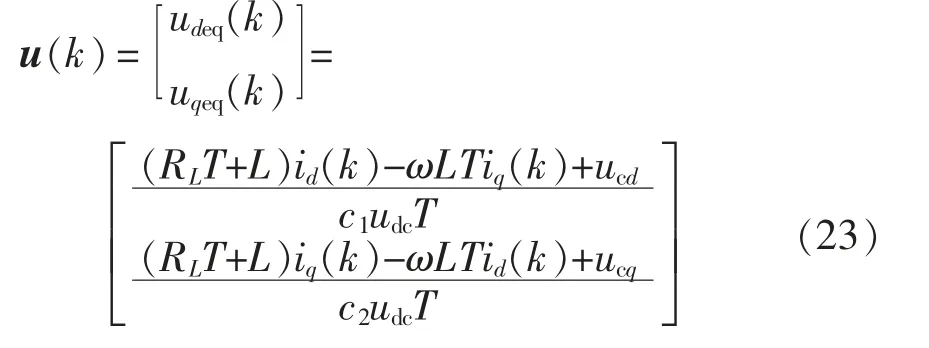
进一步利用李亚普诺夫方法对本文趋近率稳定性进行分析，李亚普诺夫函数的表达式为

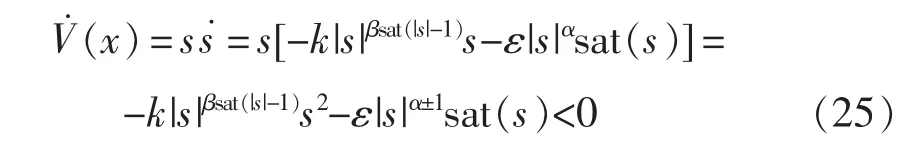
根据式（25）分析可以证明本文设计滑模控制系统的全局稳定性。此外，依据文献[22-23]分析可知，系统由初始状态到达滑模面时间与滑模变参数相关，其中当k 取值较大时，系统响应快速，然而抗干扰能力差，当ε 较大时，抗干扰能力增强，抖振现象明显，综合仿真，本文k 取为5，ε 取为3。

3 实验验证分析

3.1 仿真分析

为验证本文理论分析的可靠性，基于Matlab 仿真软件构建了完整的仿真模型。其中直流侧电压取为750 V，网侧电感为1 mH，直流输出侧额定负载为80 Ω，滤波电容C1=C2，电容值为1 080 μF，开关频率为40 kHz，仿真结果如图4、图5 所示。

不同工况下，系统工作在额定功率下的相关仿真结果包括d-q 域的电流参考信号、电网电压和电流。从图4 可以看出，输入电流与输入相电压是同相位的，与单位输入功率因数的情况吻合较好；网侧电流的THD 分别为1.43%和2.72%。为测试瞬态性能，将Vienna 整流器的输出功率由半载变为满载，并在t=0.3 s 时由满载降至半载，如图5 所示，当负载发生突变时，电网电流和直流电压迅速达到稳定状态，表明了所提SMC 仍保持快速动态响应的优势。

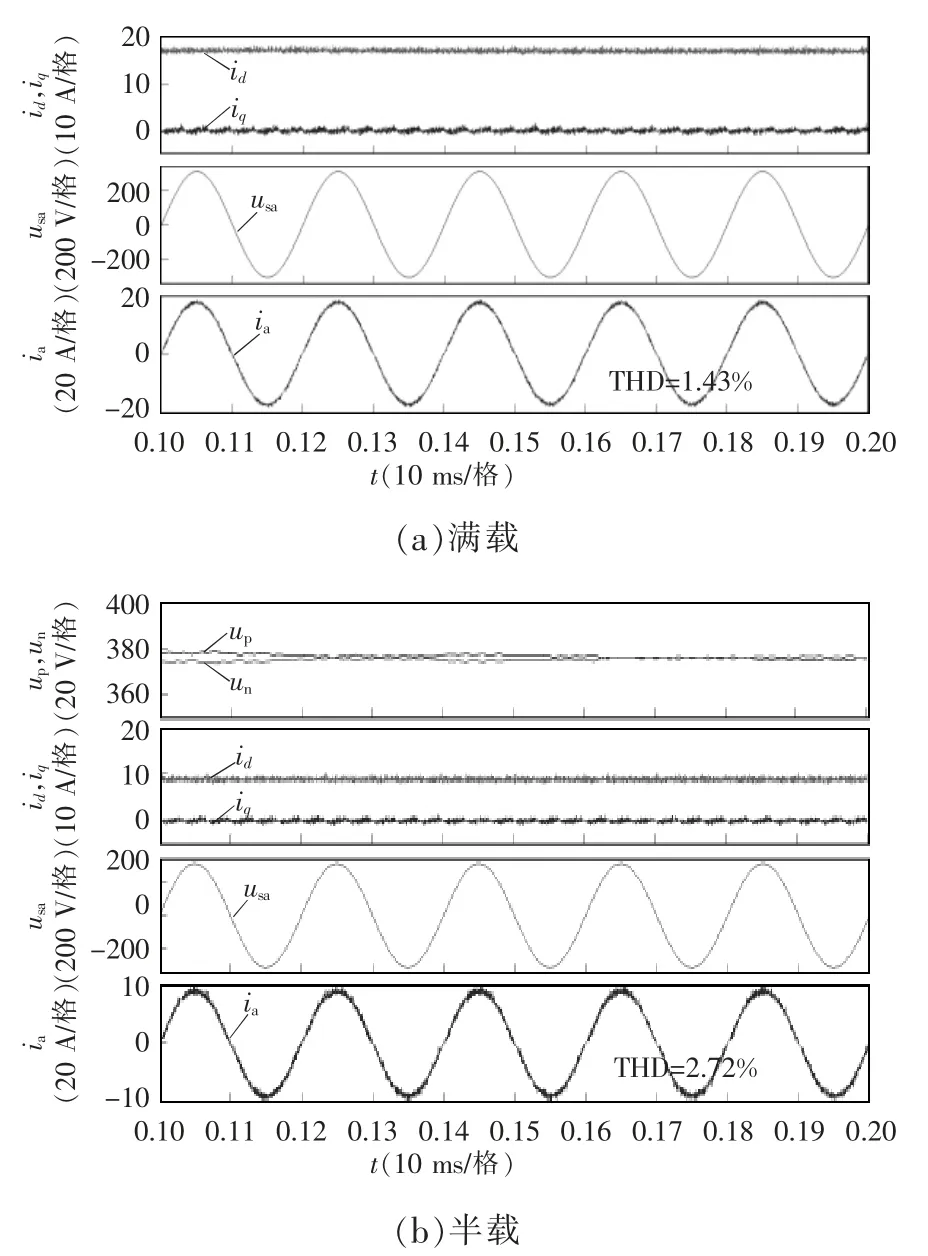
图4 不同仿真工况下静态响应波形Fig.4 Static response waveforms under different simulation conditions

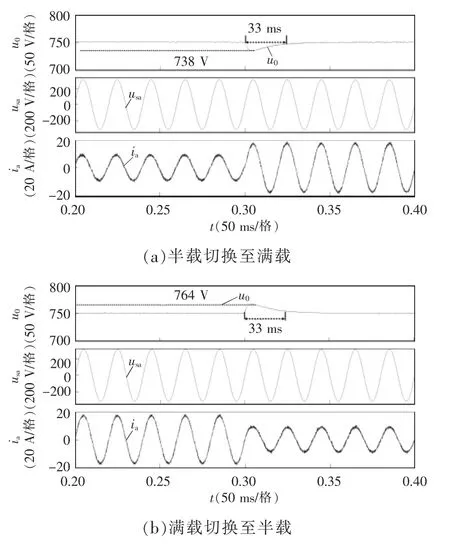
图5 不同仿真工况下动态响应波形Fig.5 Dynamic response waveforms under different simulation conditions

3.2 实验验证分析

为验证上述分析的正确性，进一步构建完整的实验样机测试模型，其中DSP 采用TMS320F283 35 控制器，双向MOSFET 开关选用SPW47N60C3，二极管选用APT30D-120BG，三相输入电压由调压器提供，电流探头型号为Tek-TCPA300，电压探头型号为P5200A，示波器型号为Tek-MDO3034。其余实验参数与仿真参数均保持一致。

不同实验工况下静态响应波形如图6 所示。图6（a）为采用本文控制方案时半载工况下的并网电流与电压输出波形，图6（b）为采用本文新型控制方案下满载运行时的并网电压、电流输出响应。对比图6（a）和图6（b）可以看到，采用本文控制方案时，其并网THD 由3.65%下降至1.85%，说明了本文所提控制策略的优越性。

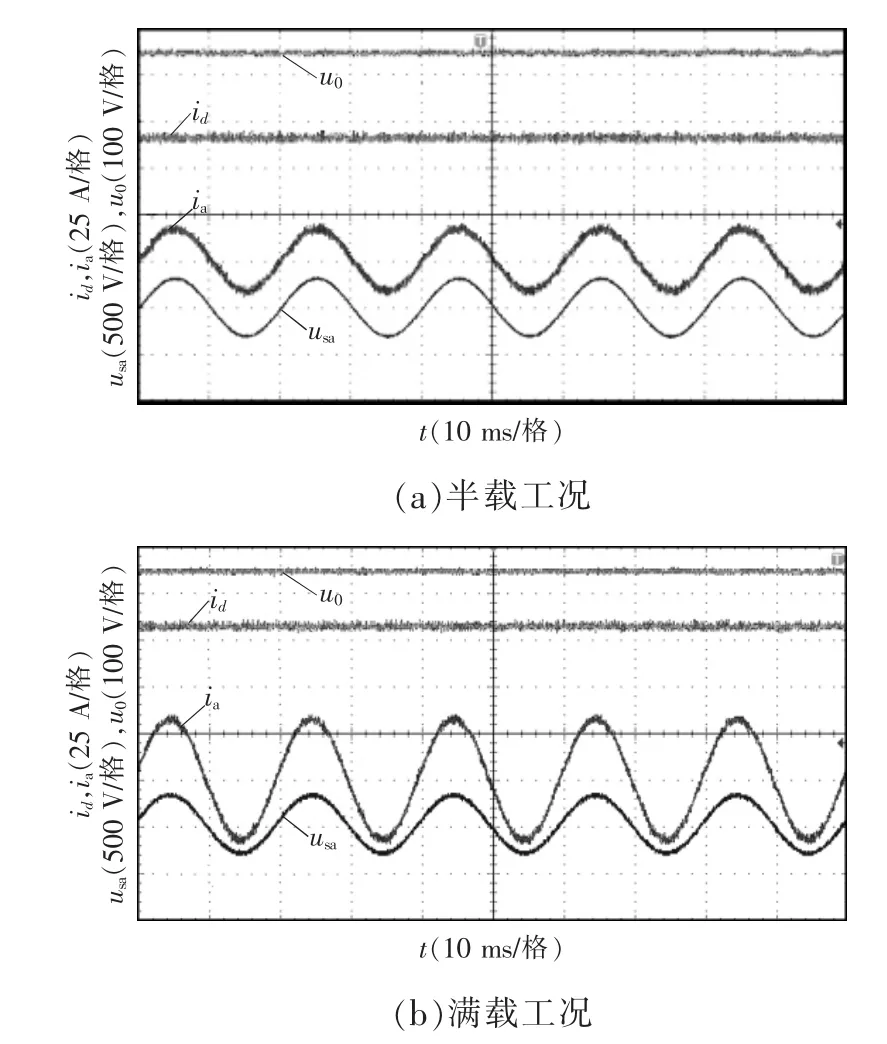
图6 不同实验工况下静态响应波形Fig.6 Static response waveforms under different working conditions

图7 给出了当系统由满载切换至半载时，采用本文SMC 控制策略下系统暂态响应波形，对比图7与图6（b）可以看到，采用本文SMC 控制方案暂态性能良好，瞬态超调现象得到有效抑制。仿真与测试结果基本保持一致，说明了本文SMC 控制方案的有效性。

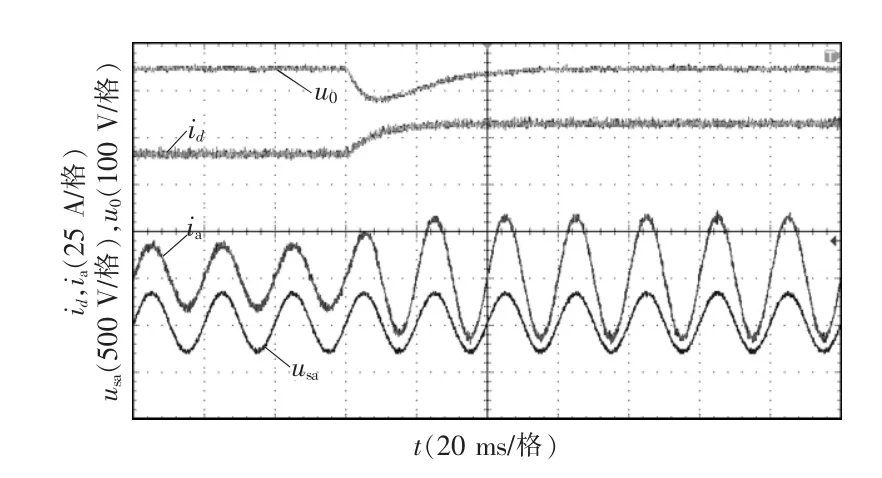
图7 实验工况下动态响应波形Fig.7 Dynamic response waveforms under working condition

图8 给出了为当给定直流输出侧负载电阻分别为75 Ω 与50 Ω 时，正、负直流母线电压与网侧电流输出波形。可以看到当直流侧输出负载失衡时，直接导致正负母线电压发生不均衡现象，有可能造成直流输出侧电容或开关管器件损坏。当引入直流中点电压均衡控制后，正负母线电压较快趋于平衡态，有效提升了整机的可靠性，测试结论与仿真分析相一致。

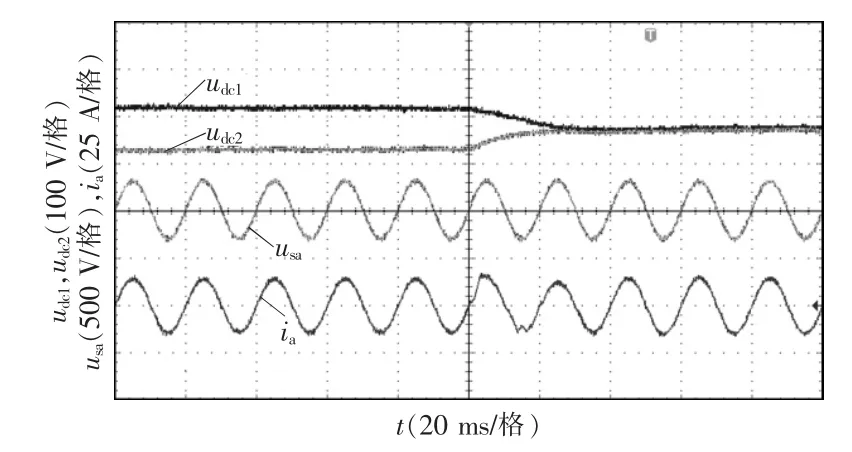
图8 直流母线电压与网侧电流输出波形Fig.8 Output waveforms of DC bus voltage and grid current

4 结语

针对传统控制策略中并网电流性能强依赖于控制器参数的缺陷，本文提出了一种带电压前馈的改进型滑模变双闭环控制方法，并结合载波SVM 调制策略将之应用于三相Boost 型Vienna 并网整流器。本文给出了详细的理论设计步骤，最后结合全面的仿真与实验验证了所提控制方案的可靠性。仿真与实验结果表明，所提改进型SMC 双闭环控制方案可以有效改善并网电流动静态性能，网侧电流谐波畸变率小；系统暂态响应快速，表明该复合控制策略具有较好的动态性能，具有较好的抗干扰能力；最后，对于直流输出侧不平衡工况进行了验证分析，表明了所提控制方案的可靠性，为三相Vienna 整流器提供了一种新型、全面、高效的控制方案。