一种SVPWM 简化算法的设计与实现

马建辉，高 佳，周广旭，朱孟美，慕永云

（1.齐鲁工业大学（山东省科学院）；山东省科学院自动化研究所；2.山东省汽车电子重点实验室，济南 250014）

空间矢量脉宽调制SVPWM（space vector pulse width modulation）技术利用8 个基本电压矢量合成电压空间矢量，使其磁链轨迹尽量逼近圆形，可以达到减少功率开关器件的开关次数、提高直流电压利用率、获得较好的谐波抑制效果的目的[1]。与传统的正弦矢量调制SPWM 技术相比，其功率开关器件的开关次数可以减少1/3，直流电压利用率可提高15%，且易于实现实时的数字化控制。因此广泛应用在三相交流电机的磁场定向控制中[3-4]。

为了使合成磁链轨迹尽量逼近圆形，从而更好地抑制谐波和转矩脉动，需要为三相逆变器设置较高的PWM 开关频率，但是传统的SVPWM 算法需要执行反正切、求正弦、求余弦的三角运算，较长的运算时间限制了PWM 开关频率的提升空间，从而限制了抑制转矩脉动和谐波的效果。文献[5-8]利用合成电压空间矢量的α、β 轴分量的若干代数关系运算结果为中间变量，判断空间矢量所在扇区号，尽管在扇区号判断环节降低了对三角函数运算的需求，但中间变量无法用于PWM 模块占空比的计算，在嵌入式实现中仍需要经过复杂的计算，得出a、b、c 三相PWM 模块的占空比。文献[9]根据Us的α、β 轴分量、Us空间位置和扇区边界的关系设计了3 个中间变量，通过中间变量的正负号直接判断空间矢量所在扇区，但其几何关系的直观性不强。

本文提出一种SVPWM 简化算法[2]，将（a，b，c）三相参考系逆时针旋转90°，形成新的（a'，b'，c'）三相参考系，使得新三相参考系的3 个轴分别和SVPWM 的扇区边界垂直。将（α，β）正交坐标系下的合成电压空间矢量Us映射到（a'，b'，c'）参考系，根据几何关系，通过a'、b'、c' 轴分量的正负号直接判断空间矢量所在扇区，并根据标幺化的a'、b'、c' 轴分量直接计算七段式SVPWM 方法下a、b、c 三相PWM 模块的占空比，最后在Simulink 下对SVPWM简化算法进行仿真验证。

1 SVPWM 基本原理

1.1 合成空间矢量

设Umg为三相交流电机中的相电压幅值，ω 为相电压频率，三相相电压幅值相同，频率相同，相位依次相差2π/3，则有

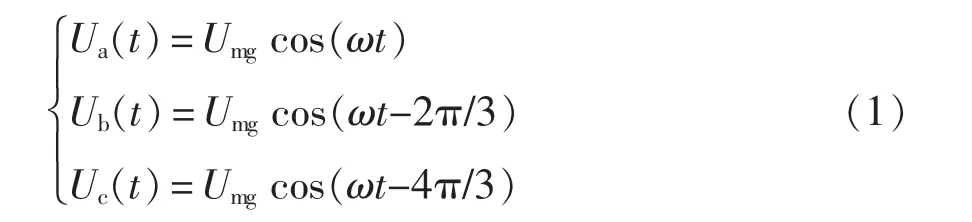
a、b、c 三相的空间分布依次相差2π/3，合成的电压空间矢量Us可以表示为可见，合成空间矢量Us是一个幅值为3Umg/2、幅角为ωt 的矢量，矢量的轨迹为圆形。

1.2 SVPWM

SVPWM 的基本原理是对图1 所示的三相桥式逆变电路中的6 个功率开关器件做有序地开关控制，使逆变器输出的三相电压的合成矢量模拟这个圆。

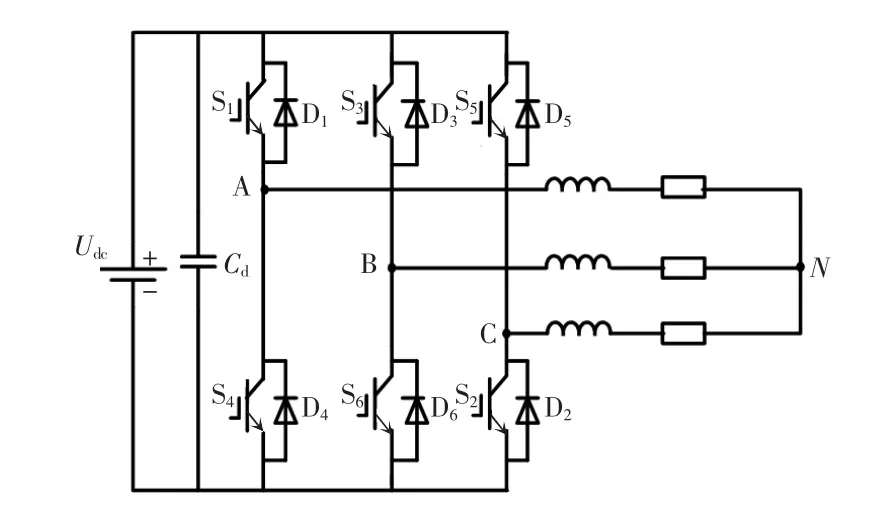
图1 三相桥式逆变器Fig.1 Three-phase bridge-type inverter

逆变器的输出电压取决于其6 个功率器件的开关状态，同一桥臂同时只能有一个处于导通状态，由此共可得8 种开关组合，产生8 个基本电压矢量。当3 个桥臂的开关同时开或同时关时，空间电压矢量的模值为0，称为零矢量，共有6 个非零矢量。这6 个非零基本电压矢量把复平面空间分为6 个扇区，如图2 所示。SVPWM 就是利用8 个基本电压矢量等效合成每个扇区中任意的合成电压空间矢量Us。

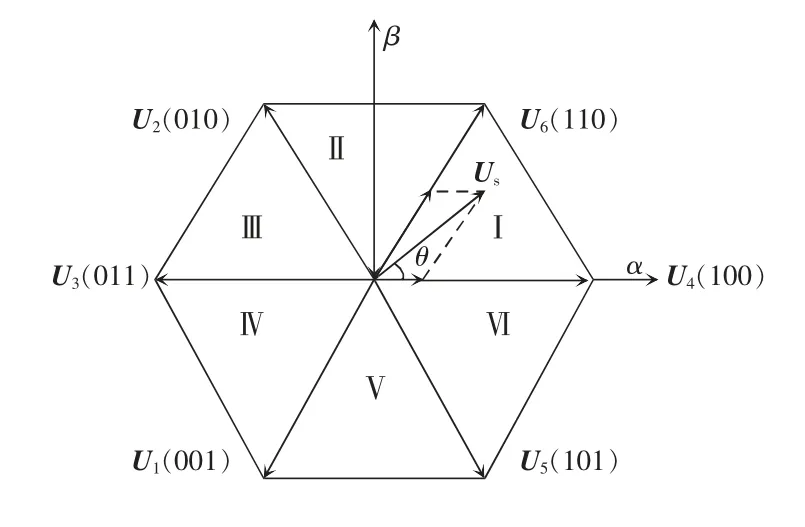
图2 基本电压矢量空间分布Fig.2 Spatial distribution of basic voltage vectors

1.3 SVPWM 算法的传统实现

SVPWM 算法的传统实现分为以下3 步：①根据α、β 轴分量判断合成电压空间矢量Us所在扇区；②计算在PWM 开关周期Ts下，扇区起始矢量、终止矢量和零矢量的维持时间Tx、Ty、Tz；③根据Tx、Ty、Tz分别计算并设置三相桥式逆变器a、b、c 相对应的PWM 模块的占空比。

判断Us所在扇区的一般方法为：将Us的α、β轴分量相除后求反正切，得到合成电压空间矢量Us和α 轴夹角θ，根据θ 判断Us所在扇区号。尽管很多MCU 厂商提供了包含求反正切函数在内的数学运算库，但其计算耗时长，影响电流环的响应速度，如果采用查表的方式计算，虽然可以在一定程度上节省计算时间，但会消耗宝贵的存储空间。而且，经过时间密集或空间密集的的三角函数运算后，其运算结果仅用于扇区判断，不能用于下一步的基本矢量维持时间和占空比的计算。

2 SVPWM 算法的简化实现

SVPWM 算法的简化实现分为2 步：

（1）建立和扇区边界垂直的新三相参考系，根据新参考系各轴分量的正负号判断合成电压空间矢量Us所在扇区；

（2）根据新参考系各轴的标幺化分量、Us所在扇区，计算并设置七段式SVPWM 方法下a、b、c 三相对应的PWM 模块的占空比。

2.1 扇区简化判断

将（a，b，c）三相参考系逆时针旋转90°，建立图3 所示的（a'，b'，c'）三相参考系。其中，a'轴和（α，β）正交坐标系下的β 轴同轴同向，与SVPWM 第Ⅰ和Ⅳ扇区的起始矢量垂直；b' 轴与SVPWM 第Ⅲ和Ⅵ扇区的起始矢量垂直，c' 轴与SVPWM 第Ⅱ和Ⅴ扇区的起始矢量垂直。

如图3 所示，（a'，b'，c'）三相参考系的a'、b'、c'轴分别和SVPWM 扇区的边界垂直，故a'轴分量、b'轴分量、c'轴分量U'c的正负号与扇区划分之间有明确的几何关系，可以根据、、的正负号判断Us所在扇区。各分量符号和扇区的对应关系如表1所示。

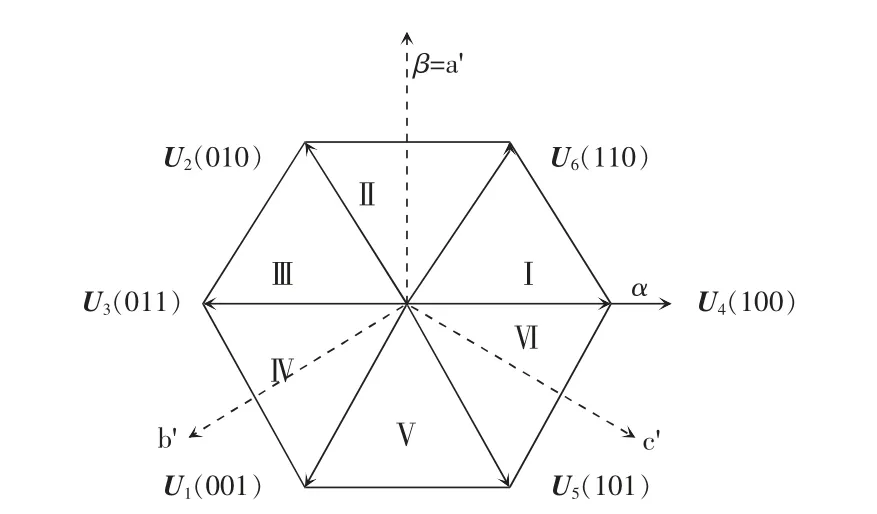
图3 （a'，b'，c'，b'，c'）三相参考系Fig.3 （a'，b'，c'）three-phase reference system

表1 扇区和、、正负号的对应关系Tab.1 Correspondence between sectors and signs of，，and

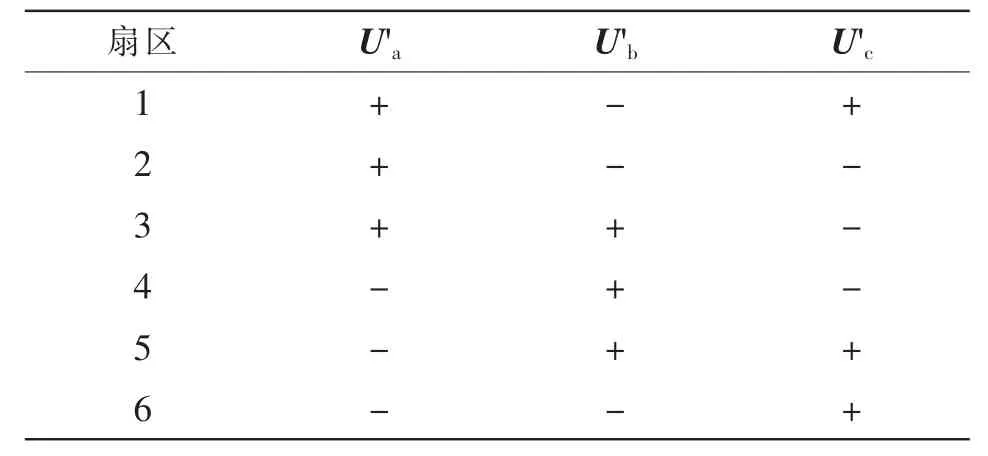
表1 扇区和、、正负号的对应关系Tab.1 Correspondence between sectors and signs of，，and

2.2 基本矢量维持时间计算

由图2 所示，第Ⅰ扇区起始矢量为U4，终止矢量为U6，根据伏秒平衡法则，可将Us分解为U4和U6两个基本矢量。

为了分析方便，以Ts为基值对Tx、Ty、Tz进行归一化处理，归一化的基本矢量维持时间以Txn、Tyn、Tzn表示。

由投影法可得

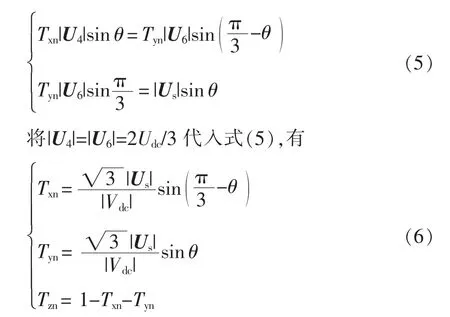
根据式（4）、式（6），结合和差化积公式计算可得

由式（7）可知，当合成空间矢量Us位于第Ⅰ扇区时，归一化的基本矢量维持时间可以从直接得出。对其他扇区情况进行分析可以得到类似的结论，在此不再赘述。

2.3 占空比计算

根据Us所在扇区起始矢量、终止矢量中a、b、c三相的上半桥导通情况，结合归一化的基本矢量维持时间，计算a、b、c 三相PWM 模块的占空比。首先以扇区1 为例计算a、b、c 三相PWM 模块的占空比，然后得出统一的简化计算公式。

2.3.1 扇区1 占空比计算

采用七段式SVPWM 方法对a、b、c 三相的输出进行调制，扇区Ⅰ中a、b、c 三相的SVPWM 波形如图4 所示。

图4 扇区Ⅰ中a，b，c 的SVPWM 调制波形Fig.4 SVPWM modulation waveforms of a，b，and c in Sector Ⅰ

扇区Ⅰ中的合成空间矢量由基本矢量U4、U6、U0、U7合成。由图4 可知，a 相PWM 模块的高电平持续时间为Tx+Ty+Tz/2，b 相PWM 模块为高电平持续时间为Ty+Tz/2，c 相PWM 模块为高电平持续时间为Tz/2。

记a、b、c 三相的PWM 占空比为Da、Db、Dc，由归一化的基本矢量维持时间Txn、Tyn、Tzn计算占空比，并代入式（7），根据（a'，b'，c'）三相参考系的标幺化分量得到扇区Ⅰ内a、b、c 三相PWM 占空比为

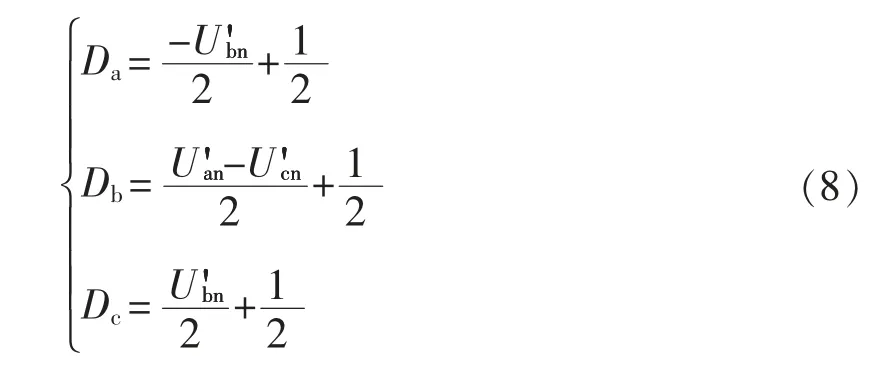
2.3.2 占空比的统一简化计算公式

对式（8）引入中间变量Ta、Tb、Tc，令

可得占空比为

对扇区Ⅱ～Ⅵ做类似扇区Ⅰ的分析。当Us位于扇区Ⅰ或Ⅳ时，令Ta、Tb、Tc按式（9）取值；当Us位于扇区Ⅱ或扇区Ⅴ时，令Ta、Tb、Tc取值为

当Us位于扇区Ⅲ或Ⅵ时，令Ta、Tb、Tc取值为

然后，统一按照式（10）计算a、b、c 三相PWM的占空比。计算出占空比后，将MCU 的PWM 模块设置为中心对齐模式，根据逆变器的开关频率和占空比设置PWM 寄存器，便可以实现对电机a、b、c三相相电压的SVPWM。

综上，SVPWM 算法流程如图5 所示。

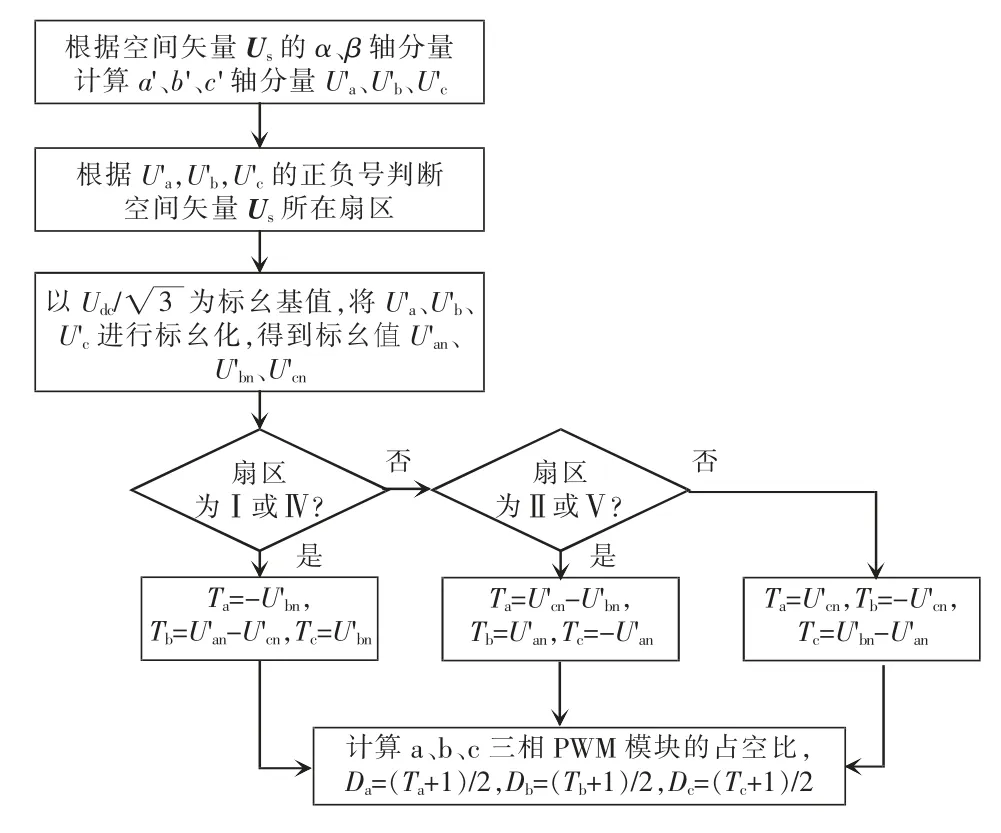
图5 SVPWM 简化算法流程Fig.5 Flow chart of simplified SVPWM algorithm

3 SVPWM 简化算法的仿真及验证

SVPWM 简化算法的Simulink 仿真模型如图6所示。仿真模型的输入为逆变器直流母线电压和相位相差90°、频率为50 Hz 的两路正弦信号，空间矢量Us由这两路正弦信号合成。模型输出为a、b、c 三相PWM 模块的占空比。选择直流母线电压为400 V，正弦信号幅值为V，以使得调制比M 为1。

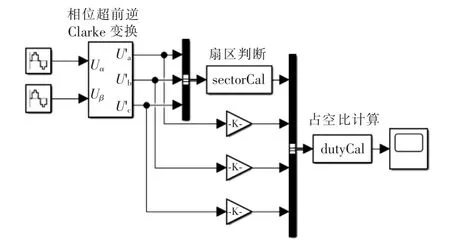
图6 SVPWM 简化算法模型Fig.6 Model of simplified SVPWM algorithm

首先，根据式（4）进行相位超前逆Clarke 变换，将合成矢量Us的α 轴分量Uα和β 轴分量Uβ转换为（a'，b'，c'）三相参考系下的a' 轴分量轴分量轴分量。通过S-Function 的方式，根据的正负号计算扇区，然后对标幺化，根据标幺化的和扇区计算a、b、c 三相PWM 模块的占空比。仿真结果如图7 所示。

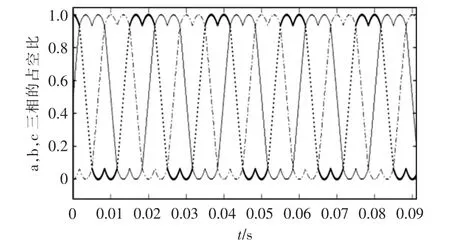
图7 SVPWM 简化算法仿真结果Fig.7 Simulation result of simplified SVPWM algorithm

为了验证SVPWM 简化算法的正确性，在Simulink 中搭建如图8 所示的对比验证模型，PWM Generator（三相两电平）的输入为400 V 的直流母线电压和幅值为V 的三相正弦信号，采用空间矢量调制方式。

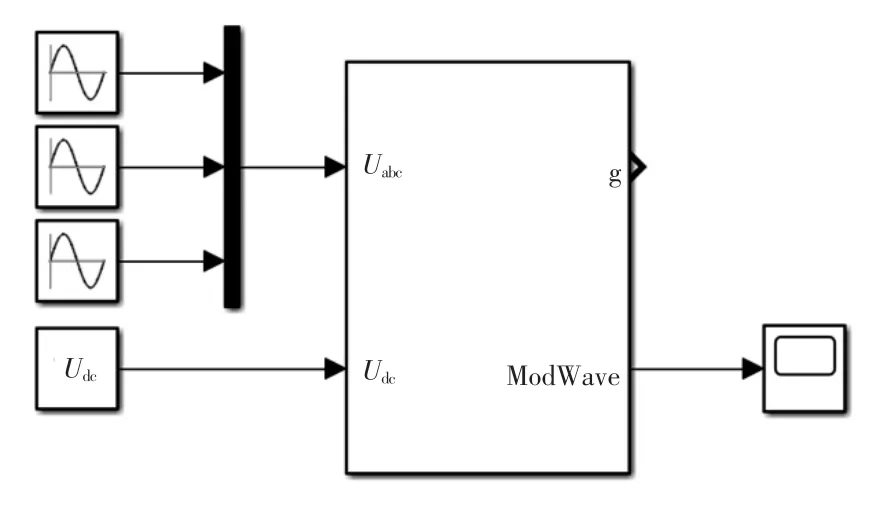
图8 SVPWM 验证模型Fig.8 Verification model of SVPWM algorithm

为了方便进行对比，将仿真生成的a 相调制波数据导入Matlab 的工作空间中，进行平移和归一化处理后调用绘图函数以实线线型绘制，将SVPWM 简化算法模型中的a 相占空比数据导入Matlab 的工作空间中，调用绘图函数以星型点阵形式绘制，对比波形如图9 所示。

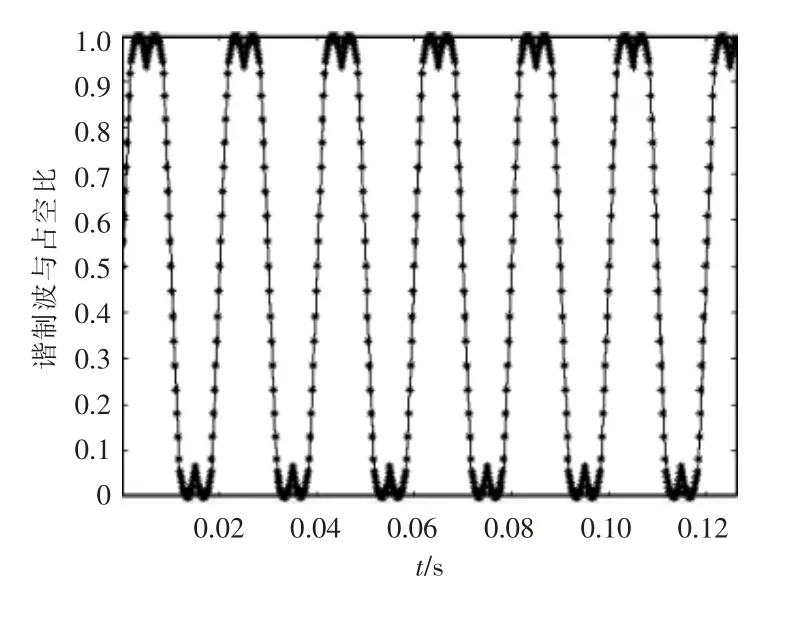
图9 波形对比Fig.9 Comparison of waveform

根据伏秒平衡原理[10]，占空比和调制波成等效关系。图9 中占空比波形和调制波波形完全一致，验证了SVPWM 简化算法的正确性。

4 结语

本文提出一种新的三相参考系，利用参考系各轴和SVPWM 扇区边界的几何关系，通过各轴分量的正负号判断合成空间矢量所在扇区，简化了扇区计算。同时，直接根据标幺化的新参考系各轴分量计算a、b、c 三相PWM 模块的占空比数据，简化了占空比的计算和设置。该方法可以降低电流环控制中的PWM 占空比更新延迟，提高电流环带宽，从而提高电机控制的响应速度。