电网电压不平衡条件下VIENNA 整流器滑模控制策略

李 山，贺梧童，郭 强，兰 蔚

（1.重庆理工大学电气与电子工程学院，重庆 400054；2.重庆理工大学重庆市能源互联网工程技术研究中心，重庆 400054）

随着电力电子变换器技术的发展，传统的两电 平整流器难以满足工业生产对整流器高频化、大功率、高电压等特点的需求，因此三电平技术受到越来越多学术界与工业界的关注[1]。VIENNA 整流器作为新型的三电平拓扑，与传统具有功率因素校正PFC（power factor correction）功能的整流拓扑相比，具有以下优点：功率开关器件少；不存在桥臂直通，无需设置死区；开关器件承受较低的电压应力[2-4]。

三相PWM 整流器控制策略的研究通常假定在三相电网电压平衡条件下进行的。但在三相电网不平衡条件下由于负序电压及负序电流的引入，会导致直流侧电压中产生2 次谐波[5]。这类2 次谐波经过调制模块，又会反射到交流侧产生3 次谐波电压及3 次谐波电流。经反复迭代，整流器直流侧电压中将出现2，4，6，…等偶次非特征谐波，在交流电流中出现3，5，7，…等奇次非特征谐波[6-7]。当电网不平衡度较为严重时，这些非特征谐波将严重影响整流器控制性能。

当电网处于不平衡状态时，各相的频率、相位、幅值将会发生变化[8]，因此，如何准确提取电网各序电压分量的参数，是三相不平衡工况下VIENNA 整流器控制策略中需首要解决的问题[9]。文献[10]提出了改进型单同步坐标系软件锁相环，有效抑制了电网电压中负序分量的影响，改善了稳态性能，但引入二倍频陷波器对系统稳定性造成了一定影响；文献[11]引入了基于双同步坐标系的解耦软件锁相环DDSRF-PLL（decoupled double synchronous reference frame-phase locked loop），该方法在正、负序双同步旋转坐标系下采用了对正负序分量的解耦算法，实现了对正负序分量的分离和频率的良好适应；文献[12]提出了一种基于滑动平均滤波器的锁相环，通过改变滑动窗长度可有效抑制多次谐波，实现了各序分量的分离并具备良好的适应性，但存在一定的延迟问题，影响系统响应速度；文献[13]提出了一种延时信号消除锁相环，通过将电网信号延迟1/4 基波周期来产生正交信号。该方法控制简单，且能有效分离正、负序电压、电流分量，但其滤波能力有限，且延迟的引入对动态性能也会造成影响。针对上述锁相环存在的一些问题，本文选用了基于双同步坐标系的解耦软件锁相环应用在VIENNA 整流器的控制中，该方法能够有效分离正负序分量，延迟很小且不会对系统稳定性造成影响，在电网电压发生频率变化时可以保证良好的准确度。

对于三相不平衡电网中VIENNA 整流器的控制策略，文献[14]提出了一种基于双同步旋转坐标系下正负序双电流内环独立控制结构，在dq 坐标系下对正、负序电流分别进行控制，再经过矢量调制模块构成VIENNA 整流器的闭环控制系统，但该方法结构复杂，待整定参数较多，稳态时直流电压仍含有明显的2 次谐波分量；文献[15]提出了一种基于无源理论的电流内环控制方法，通过选取适当的能量存储函数，根据要求确定系统期望并设计控制律，采用阻尼注入法实现不平衡条件下整流器的控制；文献[16]在静止坐标系下提出了一种电网电压不平衡整流器控制策略，该方法对整流器输入输出功率进行分析得到αβ 坐标系下电流指令值，再由双闭环控制策略实现控制目标。该方法无需对电网电压做坐标变换和相位检测，但其电流指令值计算较为复杂，控制参数不易选取；文献[17]提出了一种模型预测控制，该控制方法无需锁相环和正负序分离过程，能有效抑制有功及无功功率波动，但需建立较为复杂的开关表。

本文提出了一种基于滑模变理论的控制方法，应用在不平衡条件下VIENNA 整流器中，通过对不平衡条件下VIENNA 整流器输入输出瞬时功率进行分析，得到两相旋转坐标系下的电流指令参考值，然后在控制系统中采用双环结构，其中外环是传统的PI 环，内环通过选取合适的滑模面及趋近律得到不平衡条件下的滑模电流环。本方法无需建立复杂的开关表，有效简化了不平衡条件下复杂的控制结构及控制参数调节过程，并有效抑制了功率纹波分量和直流侧电压纹波。最后通过Matlab/Simulink 仿真验证了该方法的工作性能。

1 VIENNA 整流器的数学模型

1.1 三相平衡电网中VIENNA 整流器的数学模型

三相三电平六开关VIENNA 整流拓扑如图1所示，图中：ea、eb、ec为三相电网电压；ia、ib、ic为三相电网电流；L 为滤波电感；rs为等效串联电阻；C1和C2为直流侧上、下母线电容；RL为直流侧等效电阻；VT1～VT6为6 个二极管；Sa1～Sc2为6 个全控型开关器件；Udc1、Udc2分别为直流侧上、下电容电压；Udc为直流侧输出电压。

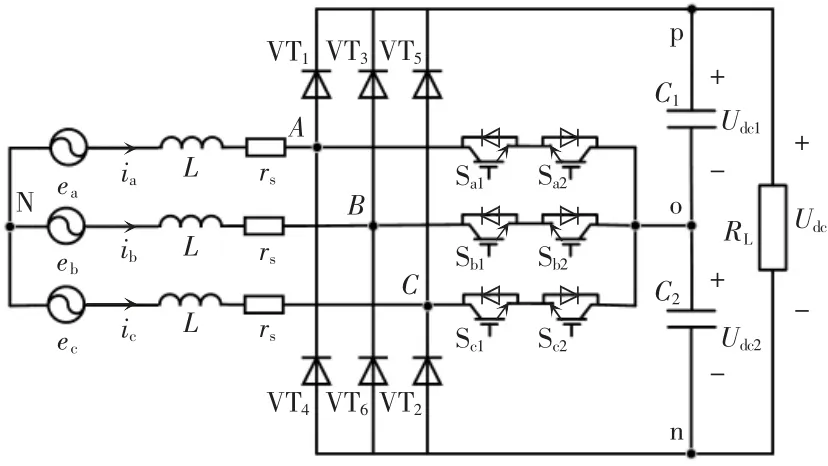
图1 三相三电平六开关VIENNA 整流器Fig.1 Three-phase three-level six-switch VIENNA rectifier

由图1 电路分析可以得到每相中的开关状态为

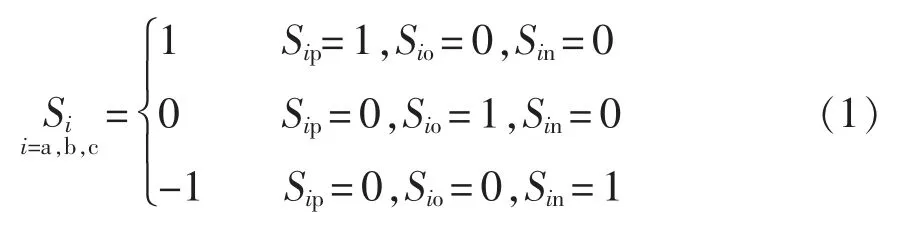
式中：下标p、o、n 分别为直流侧正电位点、中点、负电位点；Sip、Sio、Sin分别为i（i=a，b，c）相电流经由电位点A、B、C 流入直流侧正电位点p、中点o、负电位点n 时整流器的开关逻辑状态。

由图1 分析电位关系可得

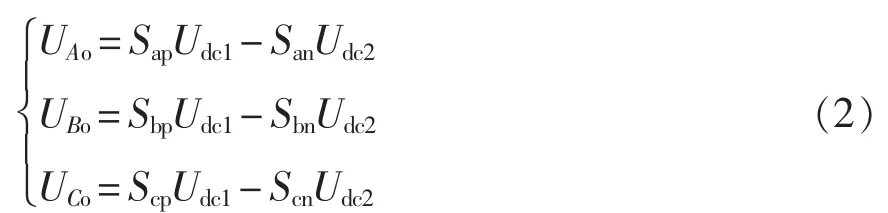
式中：UAo、UBo、UCo为电位点A、B、C 与中点o 的电位差。

对VIENNA 整流拓扑列写基尔霍夫电压定律，即

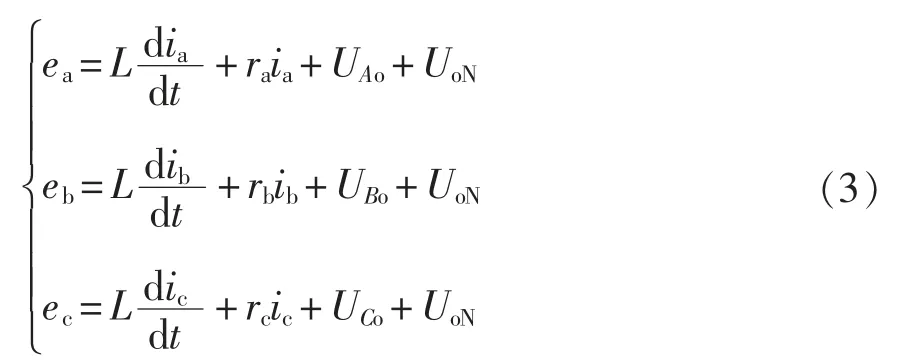
式中，UoN为中性点N 与中点o 的电位差。

对于三相对称电网有ea+eb+ec=0，ia+ib+ic=0，将式（3）各项相加后再将式（2）代入，得

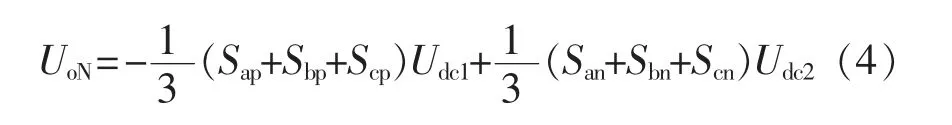
将式（2）与式（4）各项相加可得

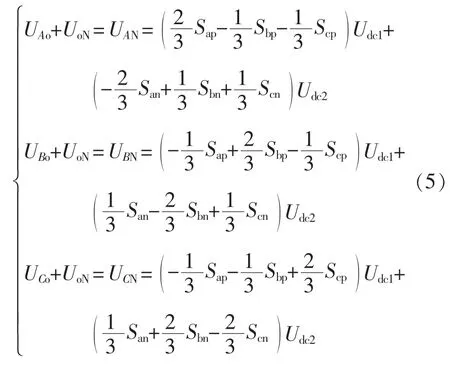
p 节点和n 节点的节点电流方程分别为

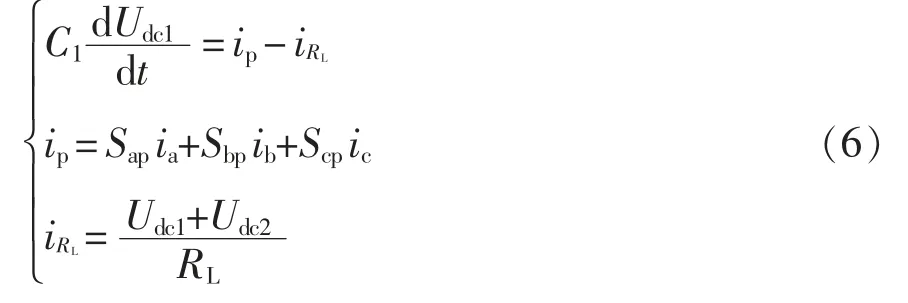
同理，n 节点的节点电流方程为

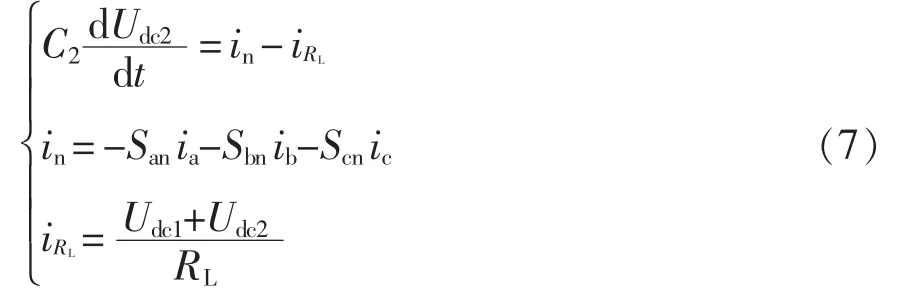
式中：ip和in分别为p节点、n节点的节点电流；rs和iRL分别为交流侧等效串联电阻和负载电流。

将式（5）代入式（3），联立回路电压方程及节点电流方程，得到VIENNA 整流器在abc 坐标系下的数学模型为

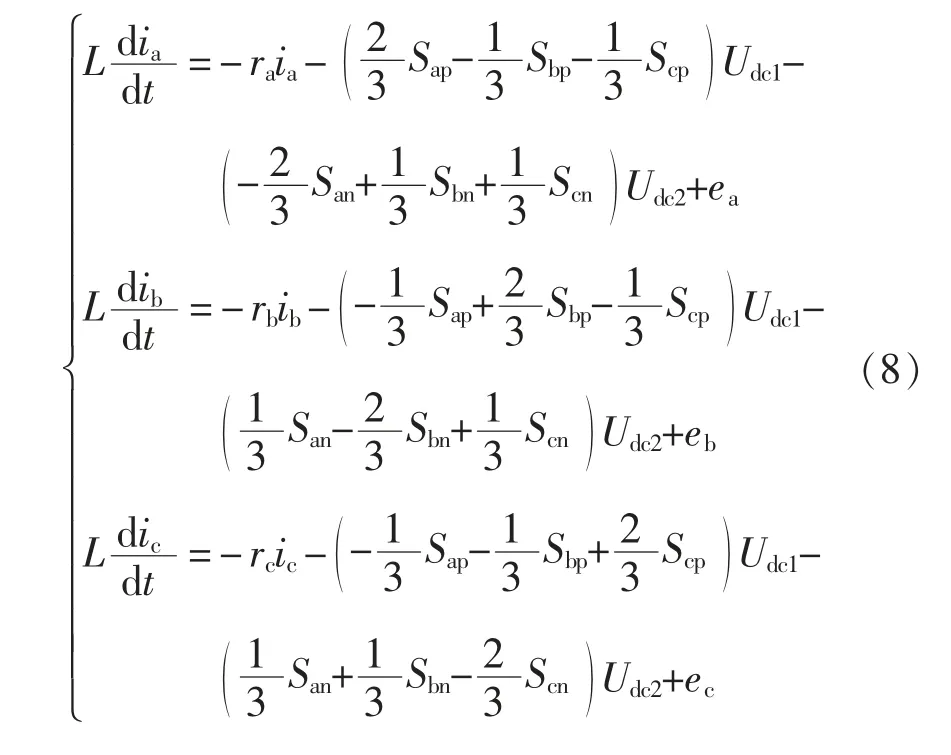
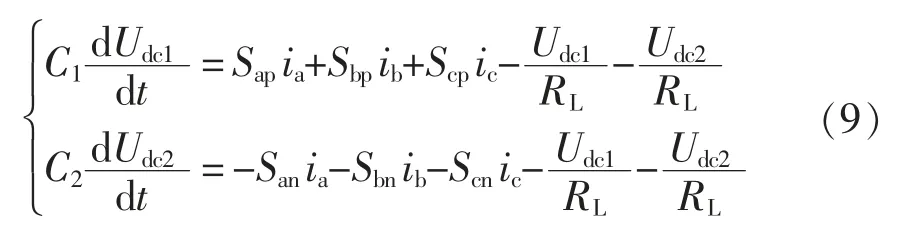
1.2 三相不平衡电网VIENNA 整流器的数学模型

当电网处于不平衡工况时，根据对称分量法，VIENNA 整流器的电网电压中会出现正序、负序和零序分量。通常在三相三线制VIENNA 整流器中，输出电容的中点与三相电网的中性点不相连，在拓扑中无零序电流通路，因此产生的零序分量可忽略，本文后续分析仅针对正、负序分量[18]。

三相电网电压在两相静止坐标系下的复矢量为

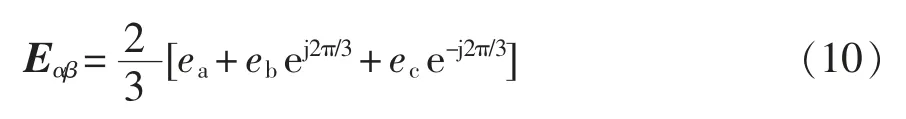
当三相电网不平衡，电网电压、电流的复矢量及整流器网侧输入端电压合成矢量均出现正、负序分量，即

根据Park 变换和Clarke 变换，由式（8）、式（9）得到VIENNA 整流器在两相静止坐标系和两相旋转坐标系下的数学模型，二者的变换矩阵T3s/2s、T2s/2r分别为

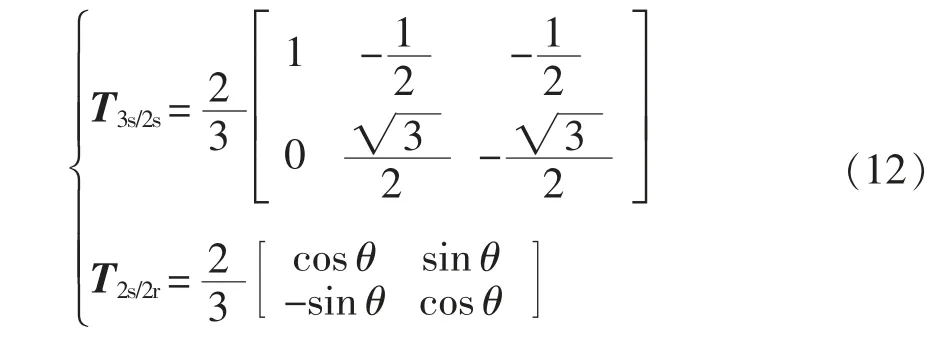
则αβ 坐标系和dq 坐标系下的数学模型分别为

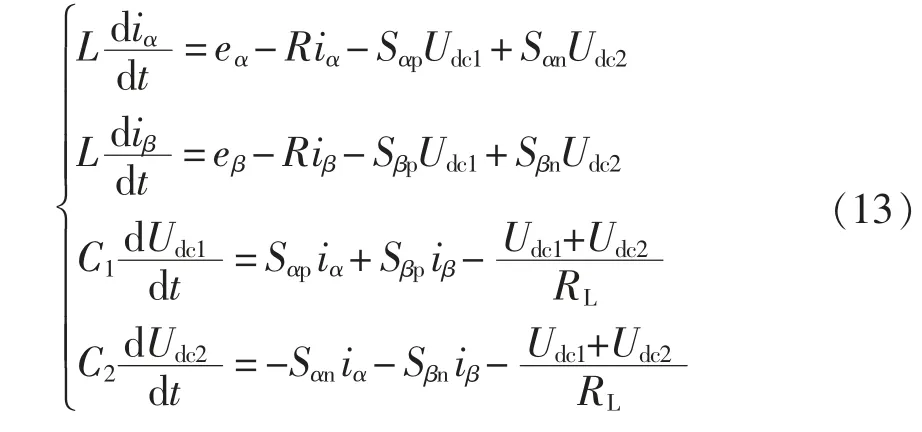
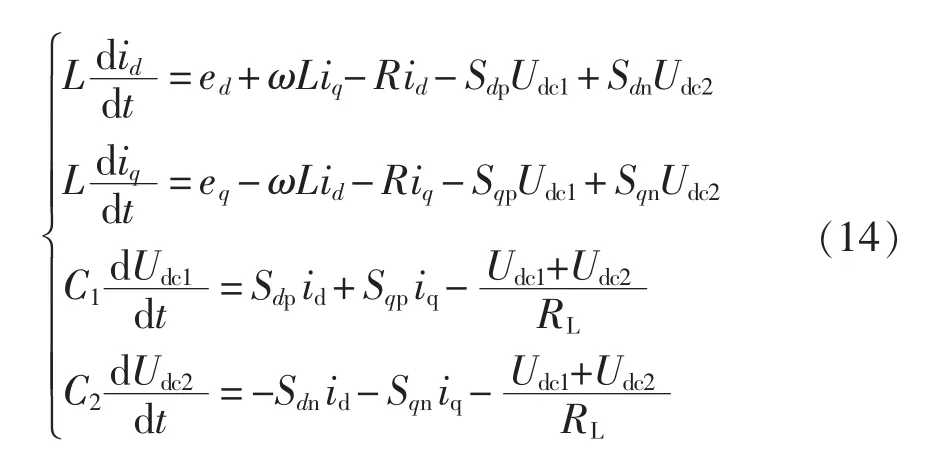
式中：iα、iβ为网侧电流的α、β 轴分量；eα、eβ为三相交流电压的α、β 轴分量；Sαi、Sβi（i=p、n）为α、β 轴下的开关函数；ω 为基波角频率；id、iq为网侧电流的d、q 轴分量；ed、eq为三相交流电压的d、q 轴分量；Sdi、Sqi（i=p、n）为d、q 轴下表示的开关函数。

由式（13）得出αβ 坐标系下VIENNA 整流器的复矢量数学模型为

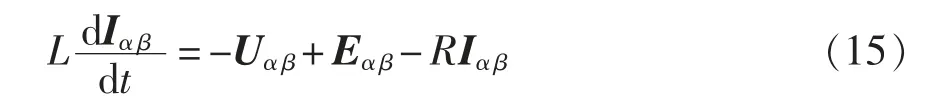
由式（14）得出dq 坐标系下VIENNA 整流器的正、负序复矢量数学模型为

该模型为本文研究三相VIENNA 整流器在电网不平衡条件下控制策略的基础。

2 VIENNA 整流器不平衡电流算法

三相电网不平衡条件下，VIENNA 整流器网侧复功率S 为

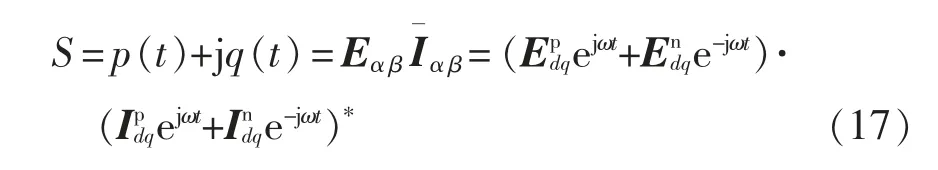
式中：上标* 为共轭运算；p（t）和q（t）分别为网侧瞬时有功功率和无功功率。

求解式（17）可得

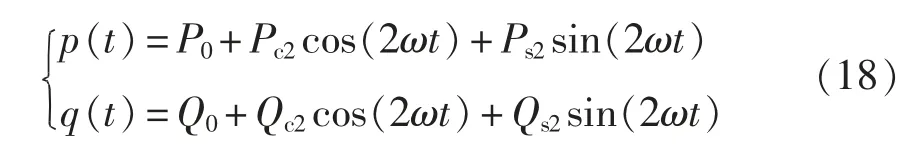
式中：P0、Q0分别为有功、无功功率平均值；Pc2、Ps2分别为有功功率的余弦、正弦项二次谐波峰值；Qc2、Qs2分别为无功功率的余弦、正弦项二次谐波峰值。

结合式（16）、式（17），将式（18）展开可得

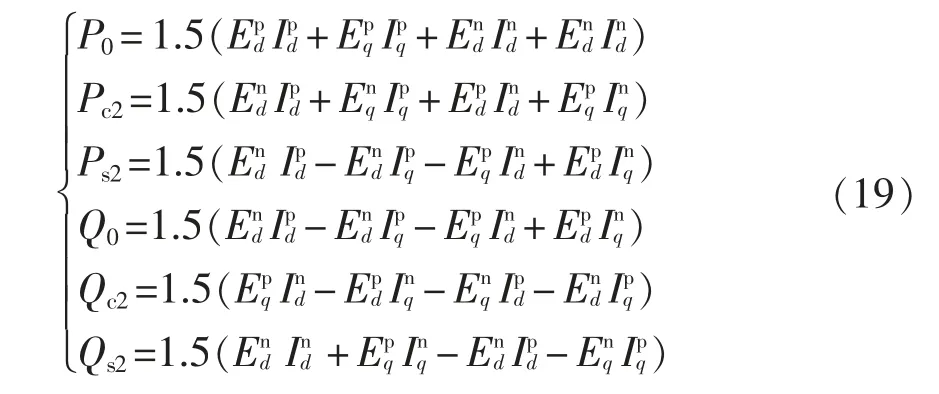
由式（18）可知，在电网电压不平衡情况下，由于负序分量的存在，三相VIENNA 整流器的p（t）及q（t）均含有二次脉动分量。若瞬时有功功率p（t）含有二次脉动分量，则直流侧输出电压也会含有二次脉动分量。

为了保证VIENNA 整流器在单位功率因数下运行，并抑制直流侧输出电压的二次脉动分量，可令Q0=Pc2=Ps2=0，代入式（18），联立式（19），整理得到抑制直流侧电压波动时电流控制指令为

联立式（13）并根据式（20）产生的电流指令，可实现直流侧电压二倍频分量的有效抑制和整流器的单位功率因数运行。但由于只有这4 个控制变量，无法同时满足Qc2和Qs2的控制需求，因此瞬时无功功率中存在二倍频分量。

3 三相不平衡时VIENNA 拓扑的控制方法

3.1 基于双同步坐标系下的解耦软件锁相环

针对三相电网不平衡时正负序分量提取及锁相问题，本文采用了基于双同步坐标系的解耦软件锁相环。

在不平衡电网中，双同步坐标系下的电压矢量如图2 所示。双同步坐标系包括2 个旋转坐标系，正序dq+1坐标系以角速度ω0沿逆时针旋转，其角度为θ0；负序dq-1坐标系沿顺时针以角速度-ω0旋转，其角度为-θ0。

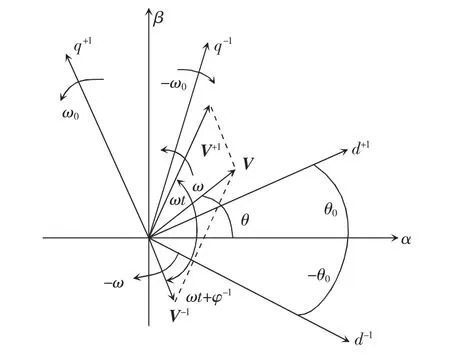
图2 双同步坐标系及坐标系中的电压矢量Fig.2 Double synchronous reference frame and voltage vectors therein

在双同步坐标系下电压矢量V 的正序和负序分量分别表示为

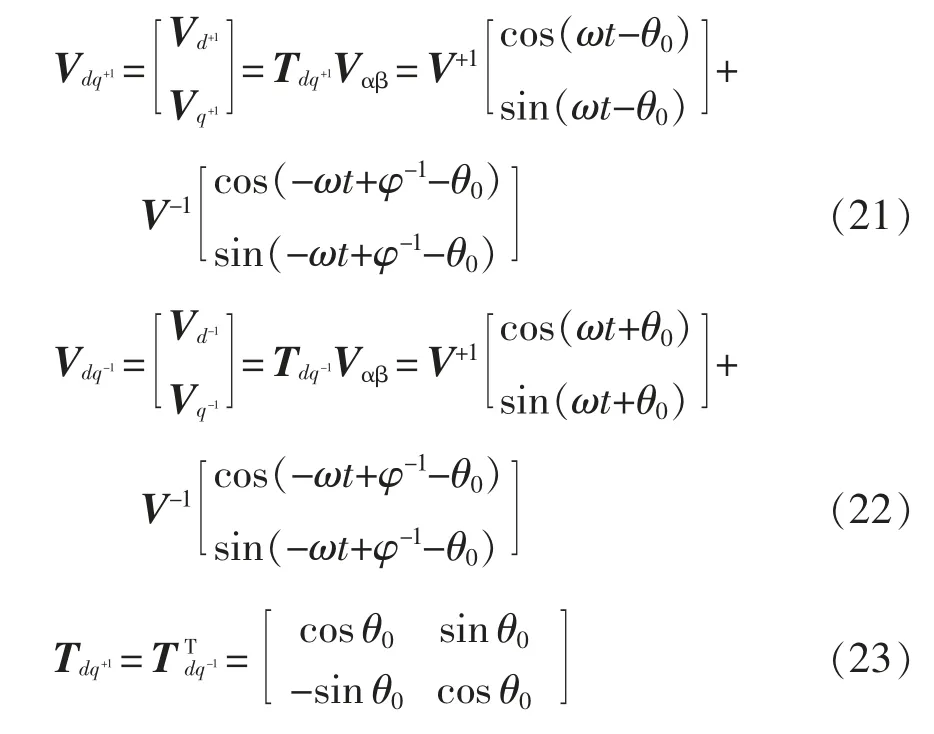
DDSRF-PLL 的原理框图如图3 所示。图3 中abc/dq+和abc/dq-分别表示abc 坐标系到正序和负序旋转坐标系的坐标变换；LPF 表示低通滤波器。通过双同步坐标系解耦下的锁相环可以准确提取电网的相位和频率，并计算出电网正、负序分量的幅值。

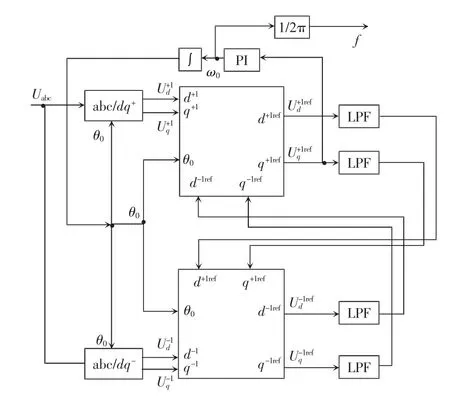
图3 双同步坐标系解耦下的锁相环原理Fig.3 Principle of DDSRF-PLL

3.2 VIENNA 整流器在不平衡条件下的控制策略

VIENNA 整流器系统的电压外环采用传统PI控制器，其内环的设计过程如下。

根据前文推导的不平衡条件下VIENNA 整流器在两相静止坐标系下的数学模型，基于滑模变理论，设置系统跟踪误差为

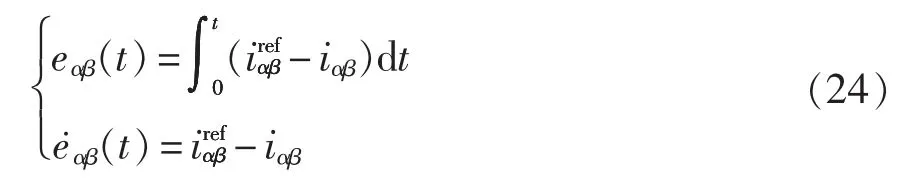
式中：eαβ（t）和αβ（t）分别为系统在αβ 坐标系下的跟踪误差及其一阶导数；iαβ和分别为αβ 坐标系下系统网侧电流实际值和参考值。

选取系统滑模面为

式中：sα、sβ分别为αβ 坐标系下系统滑模面；K1、K2为控制系数。

对式（25）求导可得

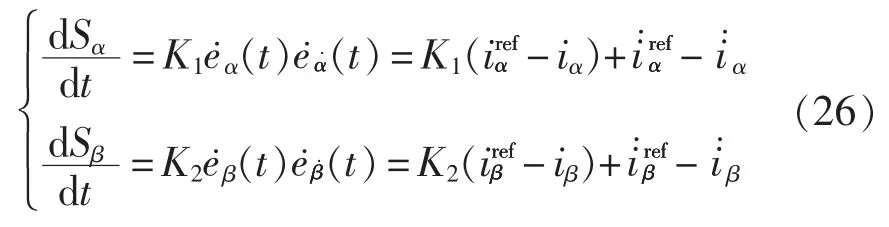
将式（26）结合VIENNA 整流器在αβ 坐标系下的数学模型，推导可得

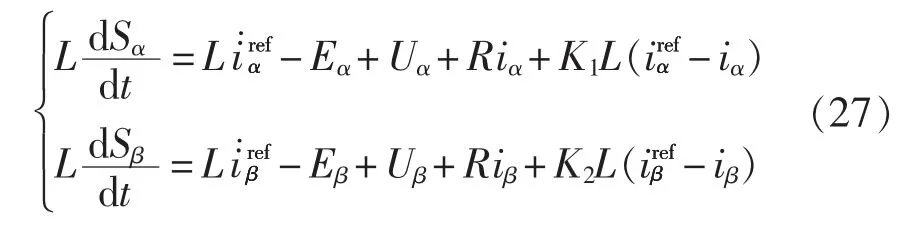
滑模运动通常包括趋近运动及滑模运动两个过程。当系统从任意初始状态趋向切换面时，最终达到切换面的运动称为趋近运动[19]。如图4 所示为系统逐渐趋于所确定的滑模面S（x）。根据滑模原理，滑模可达性条件仅保证由状态空间任意位置运动点在有限时间内到达切换面的要求，对趋近运动的具体轨迹未作限制，实际轨迹如图5 所示。因此选用合理的趋近律可以改善趋近运动的动态品质。

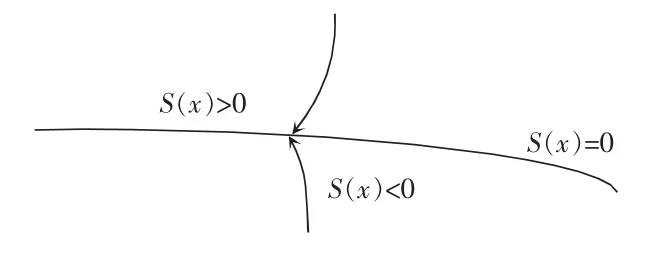
图4 系统切换面及趋近运动Fig.4 System switching surface and approaching motion

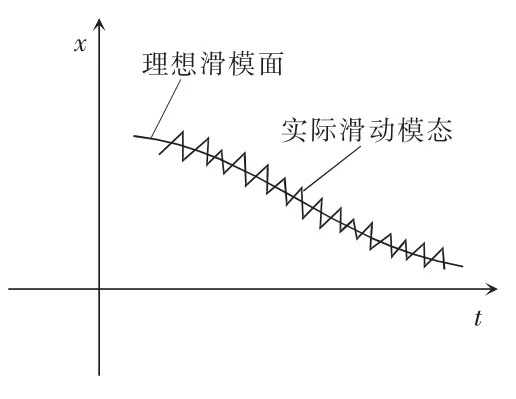
图5 滑模运动的实际轨迹Fig.5 Actual trajectory of sliding mode motion

因此，本文选用等速趋近律设计滑模变结构控制器，即有

式中：sign（）和为符号函数；Kp1和Kp2为趋近律的控制系数。

将式（28）代入式（27），移项可得两相静止坐标系下输出的控制电压为

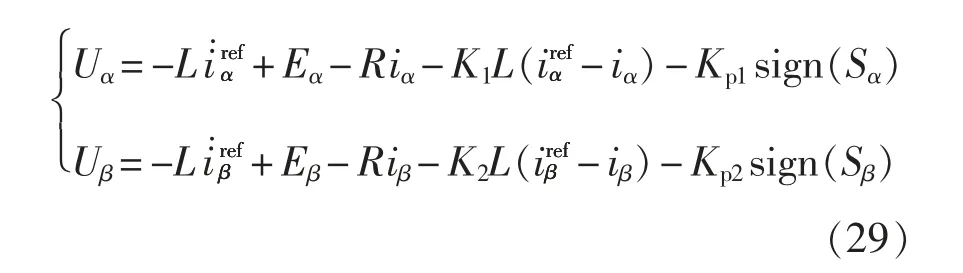
为了抑制滑模面抖振问题，滑模面系数的选取极为重要，将影响系统的稳态和动态性能。在设计系统参数时，要根据系统状态空间方程以及滑模面与滑模域的关系展开详细分析，合理选择各项控制参数，从而减小抖动对系统的影响[20]。本文所选的滑模面为

当Sα或Sβ等于0 时，收敛结果为

即当t 趋于无穷大时，误差指数收敛为0，收敛速度取决于滑模面系数K1和K2。因此合理选取K1和K2可以调整收敛速度，改善最终的动态响应时间。

本文选取的趋近律为等速趋近律，即

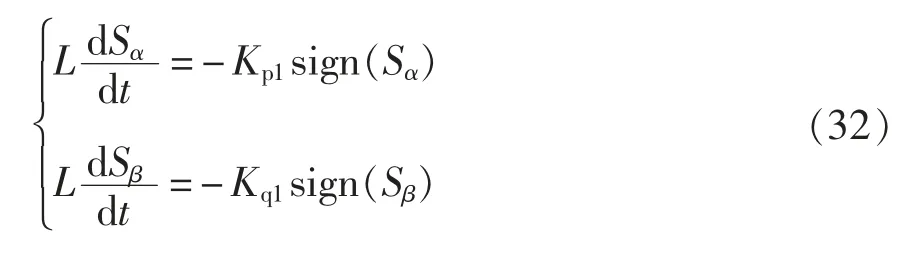
式中，Kp1和Kq1为趋近律控制系数。Kp1和Kq1越小，趋近速度越慢；Kp1和Kq1越大，趋近速度越快，同时也会引起较大的抖振现象。

本文整体的控制结构如图6 所示，其中电压外环PI 参数的设定可参考文献[21-22]。

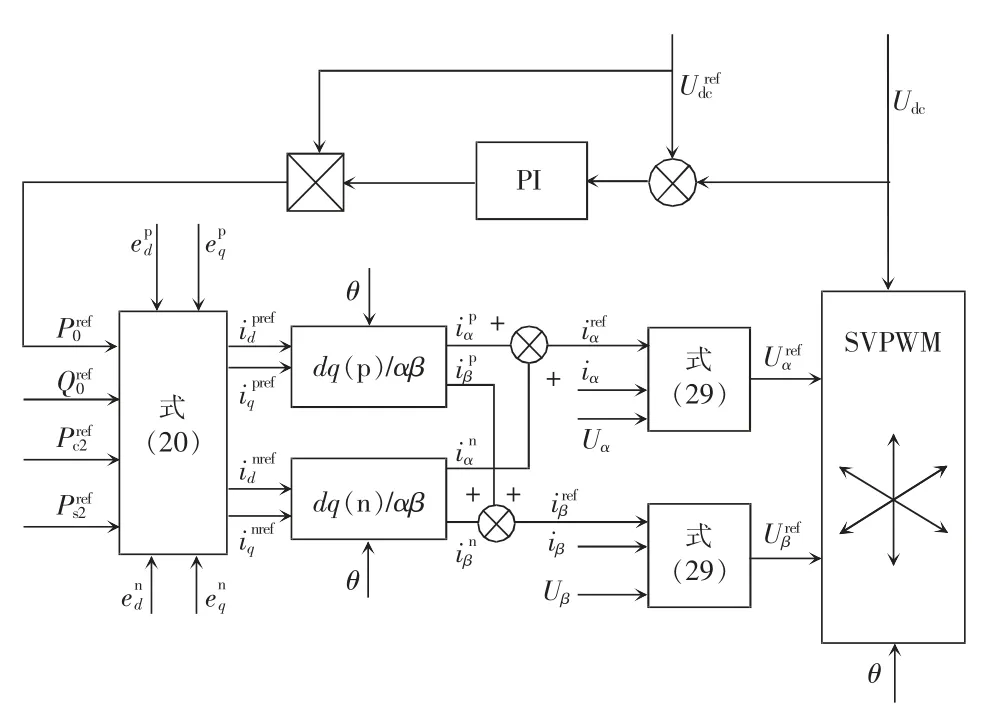
图6 三相不平衡电网中VIENNA 整流器的控制方法Fig.6 Control method for VIENNA rectifier in threephase unbalanced grid

4 系统仿真与结果分析

为验证本文所提电网不平衡下滑模变控制策略的有效性和合理性，在Matlab/Simulink 下建立VIENNA 整流器的仿真模型，其主要参数见表1。

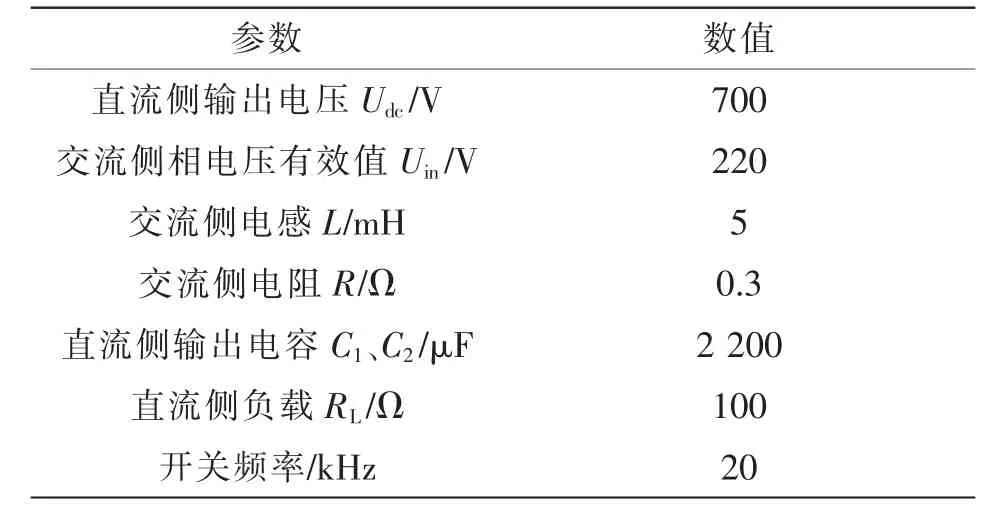
表1 VIENNA 整流器仿真参数Tab.1 Simulation parameters of VIENNA rectifier

本文选用电压跌落23%作为电网不平衡的典型情况进行分析。图7 为电网电压A 相跌落23%时VIENNA 整流器的直流侧输出电压仿真波形。可见，与传统PI 控制策略相比，本文采用的滑模内环控制策略减少了直流侧电压达到稳态所需的时间，有效改善了动态性能，且电压超调量很小。

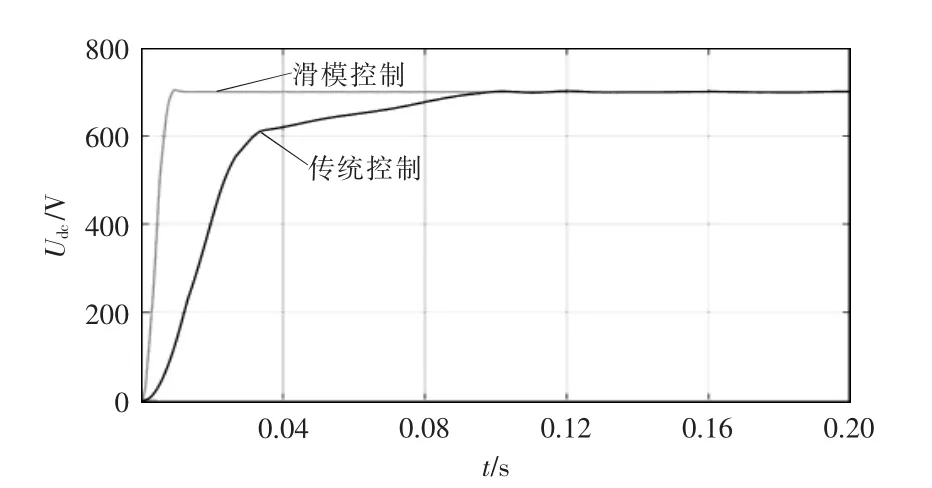
图7 三相不平衡电网下VIENNA 整流器中滑模控制和传统PI 控制的直流电压仿真波形Fig.7 DC-link voltage simulation waveforms of VIENNA rectifier under SMC and traditional PI control in unbalanced three-phase power grid

图8 为电网不平衡时两种方法的直流侧电压纹波仿真波形，可发现本文采用的方法可有效减少直流侧电压纹波。输入有功功率和无功功率如图9所示，可以看出，本文采用的方法以直流电压纹波的抑制为控制目标，可有效抑制输入有功功率的二倍频分量，但输入无功功率仍存在二倍频分量，而传统控制策略则会引入三相间有功功率和无功功率的波动。

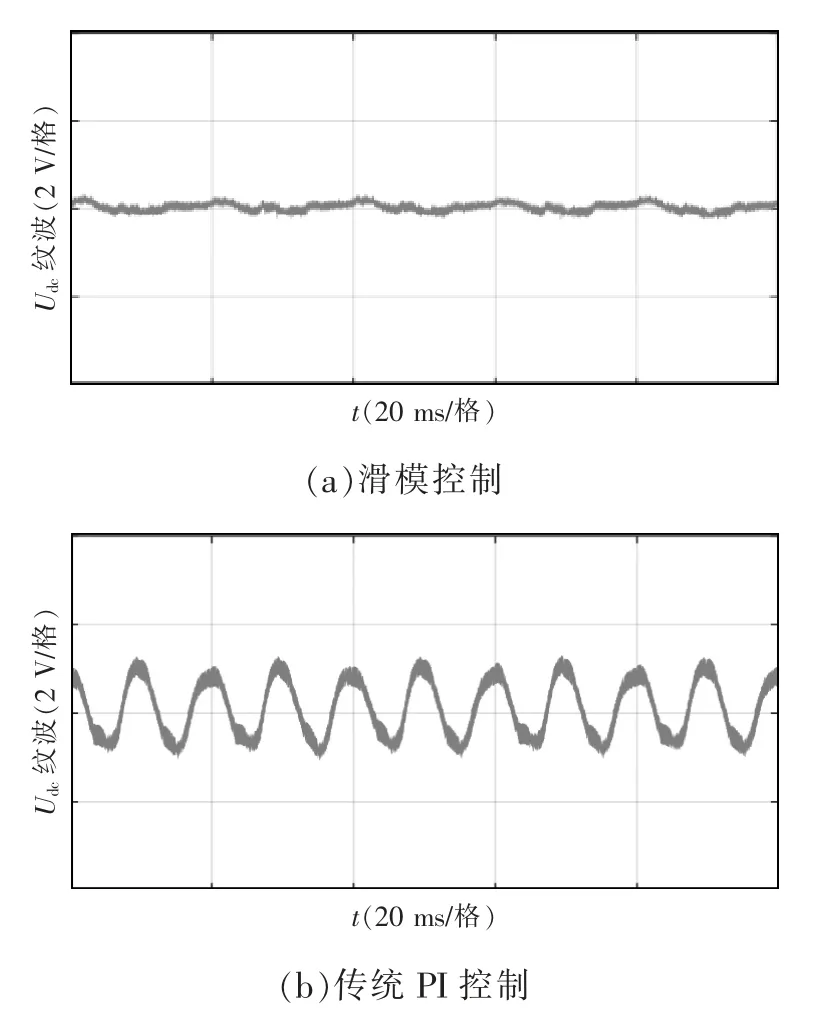
图8 三相不平衡电网中VIENNA 整流器中滑模控制和传统PI 控制的直流侧电压纹波波形Fig.8 DC-link voltage ripple simulation waveforms of VIENNA rectifier under SMC and traditional PI control in unbalanced three-phase power grid

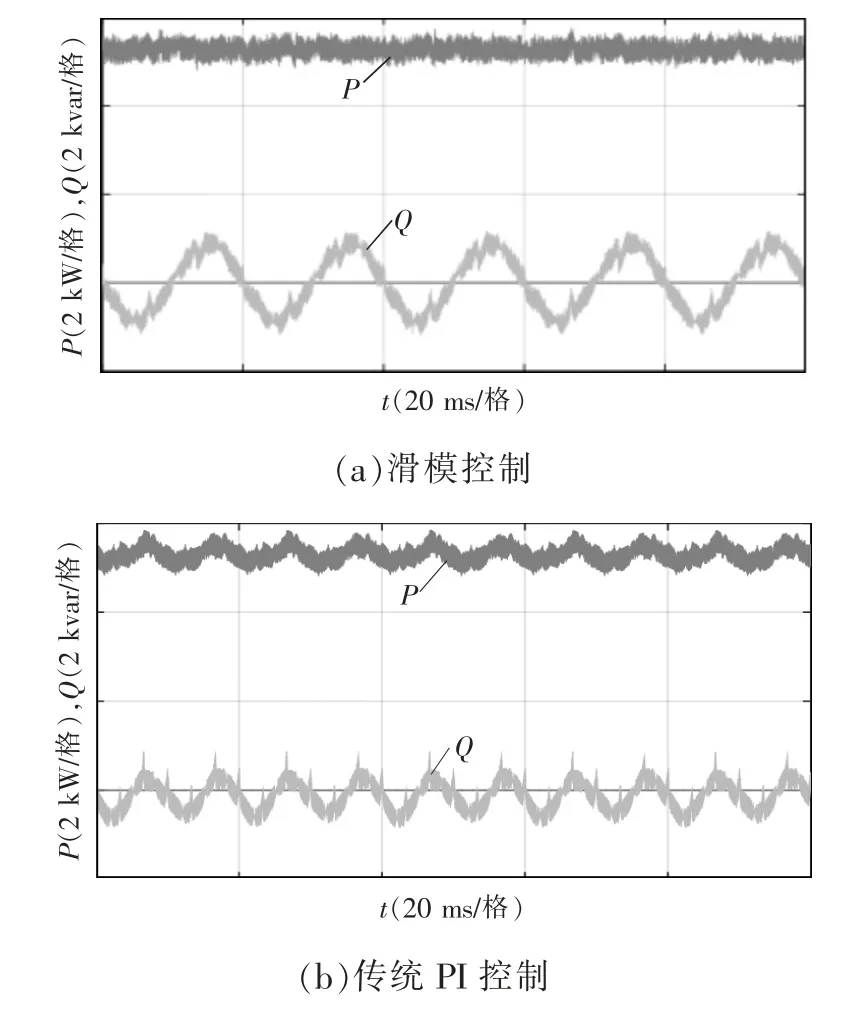
图9 输入有功功率和无功功率Fig.9 Input active power and reactive power

图10 和图11 分别为网侧三相输入电流波形和网侧三相电流的总谐波分量，可以看出，相对于传统方法的三相电流波形，本文采用的方法对各次谐波的抑制非常有效，而总谐波含量仅为1.98%。

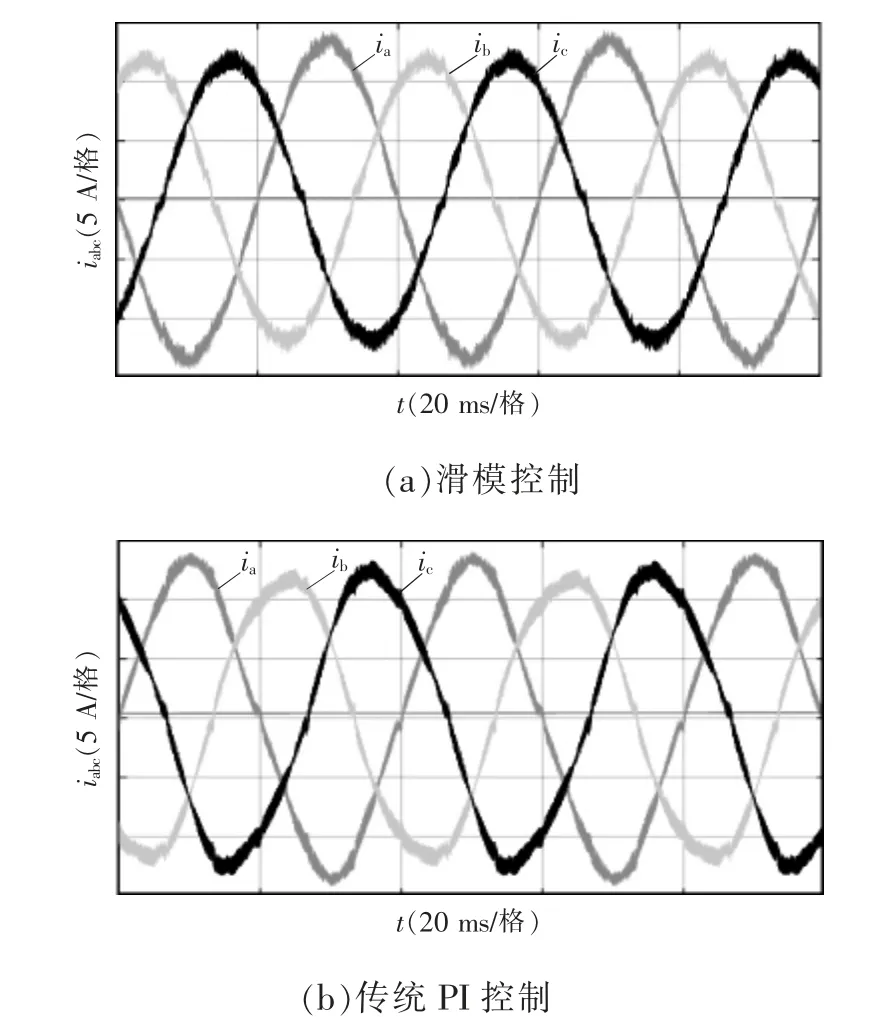
图10 三相输入电流波形Fig.10 Waveforms of three-phase input current

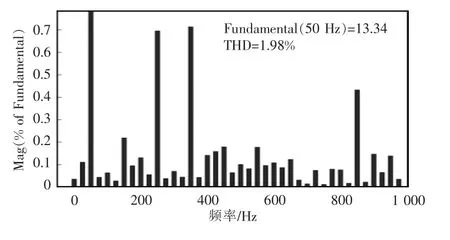
图11 网侧电流的总谐波分量Fig.11 Total harmonic component of grid-side current

5 结语

本文将滑模变原理引入到三相VIENNA 整流器中，通过不平衡电网下的电流算法实现了对正弦交流信号的无差跟踪，实现了不平衡情况下VIENNA 整流器直流侧输出电压的无纹波控制，并且可以有效抑制交流侧电流的各次谐波分量。相对传统的PI 控制器，本文策略简化了不平衡系统的控制设计及设计参数的选取和调试过程。最后，通过Matlab/Simulink 验证了本文方法在抑制直流侧电压纹波和输入有功功率二倍频分量上的优良性能。