基于模型预测的MMC-RPC 直接功率控制策略

宋平岗，杨长榄，龙日起，雷文琪

（华东交通大学电气与自动化工程学院，南昌 330013）

由于我国传统铁路牵引供电系统采用单相交流电，且机车负载具有非线性和不对称的特点，所以牵引网存在功率因数低、谐波含量高、产生大量负序电流等一系列电能质量问题，对牵引供电系统的安全稳定运行造成威胁[1-2]。为综合治理牵引供电系统的负序电流，补偿无功功率，抑制机车所带来的谐波问题，日本学者提出了铁路功率调节器RPC（railway power conditioner）这一解决方案，以其优异的治理效果和通用性受到了国内外专家学者广泛的关注和研究[3-8]。传统的RPC 需通过降压变压器接入牵引供电系统27.5 kV 母线，存在开关器件耐压水平有限，需要使用降压变压器等问题，不利于大规模推广运用[3]。有学者提出了由两个单相H桥型的模块化多电平换流器SPH-MMC（single phase H-bridge modular multilevel converter）背靠背连接构成的新型RPC（MMC-RPC）补偿装置，不仅可实现传统RPC 的所有功能，还具有能够提高电压功率等级、无需降压变压器可直接接入牵引网等优点[4-5]。

为了使RPC 更好发挥自身优越的牵引供电系统电能质量综合治理效果，对其控制方法的研究尤其重要。文献[6]采用电压外环、电流内环的双闭环比例积分PI（proportional integral）控制，实现对有功、无功分量的独立控制，较为精确快速地对牵引供电系统进行电能质量的综合治理，但PI 控制器对于稳态误差不能很好地消除；文献[7]针对MMCRPC 系统的非线性特性，提出一种基于微分平坦理论的MMC-RPC 直接功率控制策略，采用前馈控制与反馈控制相结合的方法构造MMC-RPC 功率控制器，无须建立精确的数学模型，提高了系统的抗扰动能力，但PI 环节过多，运算速度较慢；文献[8]考虑供电臂电压波动，提出一种RPC 多目标优化设计方法，并采用粒子群多目标算法进行优化，得到最优的有功、无功功率补偿指令值，既有效降低了两供电臂的电压波动，又有效减少了RPC 的补偿容量，但算法复杂，工程实际中较难实现。

模型预测控制以其控制简单、高鲁棒性、优越的动稳态性能等优点受到广大学者的关注[9-11]。文献[12]针对永磁同步电机提出了一种三矢量模型预测控制策略,在一个控制周期内施加3 个电压矢量以获取高精度的电流控制，降低了变换器开关频率，同时提高了电流环稳态性能；文献[13]把模型预测电流控制引入单相PWM 整流器，预测下一个控制周期的dq 轴电流分量，并结合最小电流误差评价函数得出最优调制函数，消除了稳态电流误差，提高了系统动态响应；文献[14]针对低惯量交流系统的频率偏移问题，采用模型预测控制算法并将其运用在VSC-HVDC 系统中，能够有效限制交流系统频率的变化，加快频率恢复的速度。而将模型预测直接功率控制运用到MMC-RPC 对牵引网进行电能质量综合治理，尚未有相关文献进行报道。

本文针对MMC-RPC 提出基于模型预测的直接功率控制策略，以V/v 牵引变压器为例，建立了MMC-RPC 的数学模型和功率预测模型，分析了功率补偿原理，以功率误差最小为原则得出目标函数，并加入延时补偿，得到最优化的SPH-MMC 交流端口电压期望值进行两相桥臂的调制。在Matlab/Simulink 分别搭建了基于MPDPC 控制、直接功率控制和双闭环PI 控制的MMC-RPC 仿真模型，仿真结果验证了MPDPC 控制策略的优越性和可行性。

1 MMC-RPC 基本原理与建模

采用三相V/v 牵引变压器的MMC-RPC 铁路牵引供电系统结构简化图如图1 所示。MMC-RPC 由2 个结构相互对称、背靠背相连的单相SPH-MMC组成，并联到左右两侧供电臂。V/v 变压器原边的3个端子分别与公用电网的A、B、C 三相连接，iA、iB、iC分别为流入变压器的三相电流。定义与牵引变压器副边左右两侧供电臂相接分别为L 侧、R 侧，uj（j=L、R）为j 侧供电臂电压，ij为变压器副边电流，ijk（k=a、b）为j 侧供电臂流入RPC 的电流，且定义is=ija=-ijb。图1 中的MMC-RPC 为四桥臂结构。每相桥臂由上下两个桥臂组成，上下桥臂均由N 个相同的子模块SM（sub-module）串联而成，子模块示意图如右侧虚线框所示。定义下标“p”、“n”为与上桥臂、下桥臂有关的量；ukp、ukn表示k 相上下桥臂N 个子模块电压之和，ikp、ikn表示流过k 相上下桥臂的电流；ejk表示j 侧桥臂交流端口对地节点电压；Rs、Ls为线路等效电阻和电感；R0、L0为桥臂等效电阻和电感；udc、idc分别为直流环节的电压和电流。

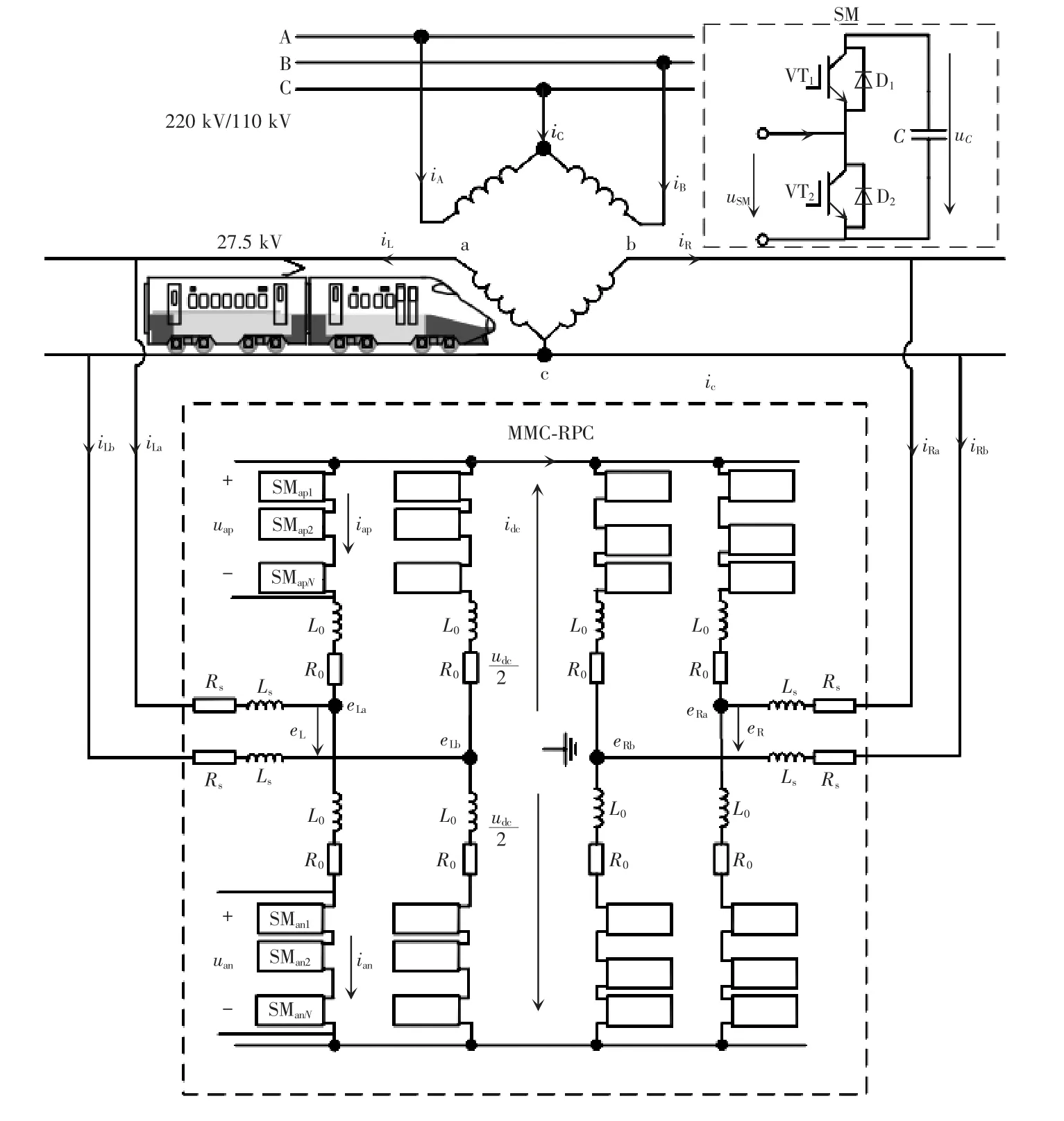
图1 MMC-RPC 结构简化图Fig.1 Simplified diagram of MMC-RPC structure

由基尔霍夫电压定律可得SPH-MMC 交流侧的数学表达式为

式中，ej为SPH-MMC 输出交流端口的电压，ej=eja-ejb。

对于SPH-MMC 的中间直流侧，满足

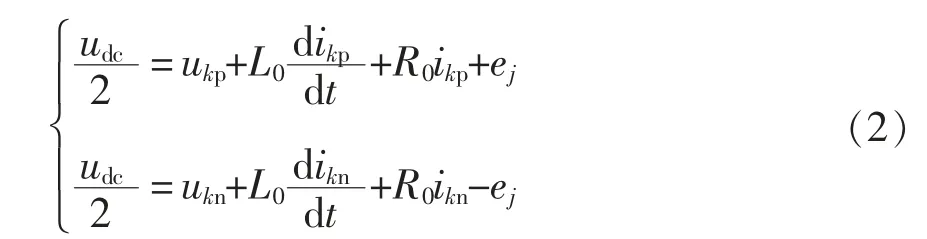
将式（2）中两个方程相加，可得SPH-MMC 直流侧电压为

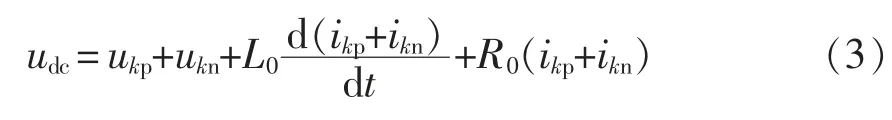
将式（2）中两个方程相减，可得SPH-MMC 交流端口电压为

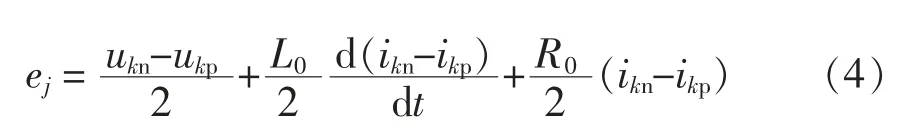
由式（3）和式（4）可知，通过控制SPH-MMC 上下桥臂子模块的投切可实现对直流侧电压和交流端口输出电压的有效控制，进而达到MMC-RPC 对牵引供电系统电能质量进行综合治理的效果。

2 V/v 牵引变压器功率补偿原理

由于供电区间的牵引负载不均衡，左右两侧供电臂的机车负载功率不同，会使牵引变压器原边存在较大的负序电流。在铁路线路上运行的电力机车运行过程中会向牵引网注入谐波，同时机车也产生大量的无功功率，故要对其进行补偿，进行牵引供电系统的电能质量治理。本文从功率角度出发，针对传统牵引供电系统的电能质量问题，以V/v 牵引变压器为例进行功率补偿指令分析，图2 为RPC功率补偿前后的矢量。uA、uB、uC分别为V/v 牵引变压器原边的三相电压矢量，pj为左右两侧供电臂负载的有功功率，qj分别为左右两侧负载的无功功率，、分别为功率补偿后左右两侧供电臂的期望有功、无功功率。由矢量关系分析，MMC-RPC 从轻载侧供电臂转移大小为|pR-pL|/2 的有功功率至重载侧，使得=。为补偿无功并消除负序电流，则需分别补偿无功功率，使补偿后原边电流达到三相对称。令pj_ref、Qj_ref分别为MMC-RPC 需要对j 侧供电臂补偿的有功和无功功率，则有

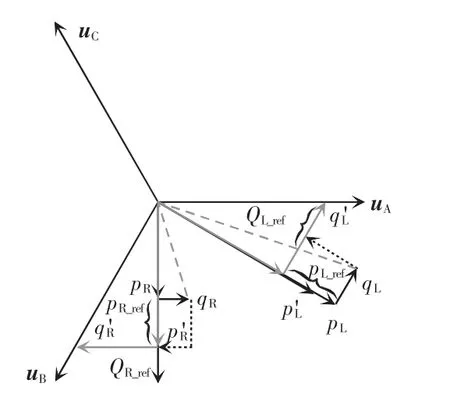
图2 RPC 功率补偿前后的矢量Fig.2 Vector before and after RPC power compensation

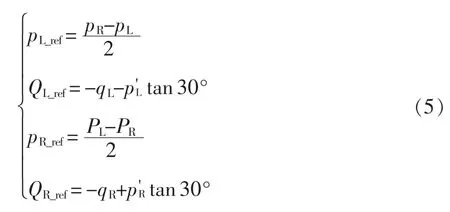
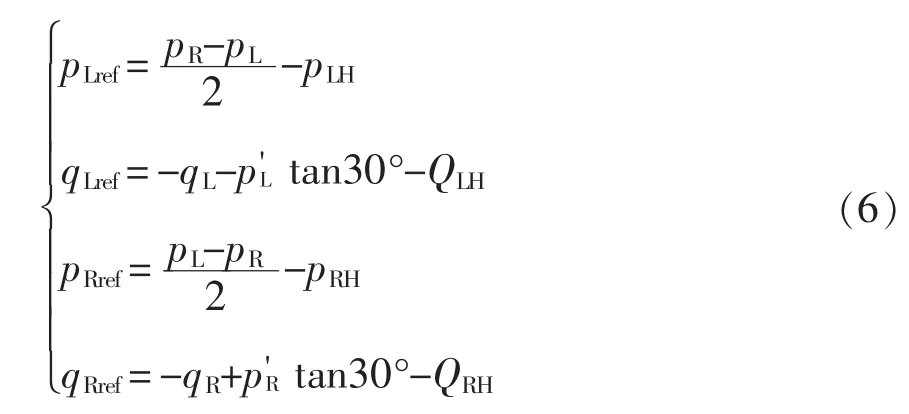
3 模型预测直接功率控制

3.1 模型预测直接功率控制原理

由于牵引网的左右两侧供电臂上为单相交流电，无法如三相交流系统一样直接由瞬时功率理论计算其瞬时有功和无功功率，因此必须构造与实际交流量正交的虚拟分量。本文采用二阶广义积分器SOGI[16]（second-order generalized integrator）来构造与电压、电流正交的虚拟分量，即式（1）可转换为

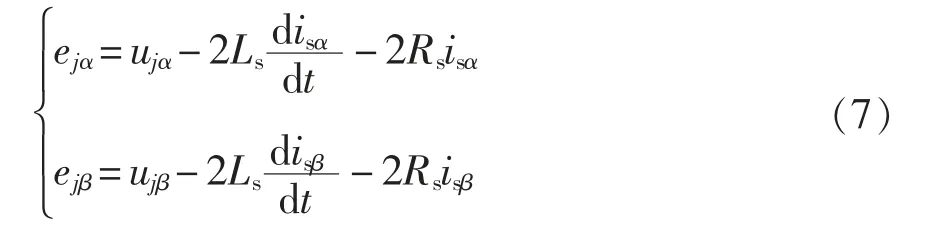
设两侧供电臂电压在α、β 轴上的分量分别为ujα=Umcos（ωt）、ujβ=Umsin（ωt），分别对isαβ和ujαβ求导得

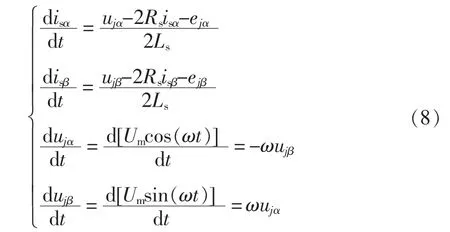
由瞬时功率理论，SPH-MMC 输出交流端口的瞬时有功、无功功率为

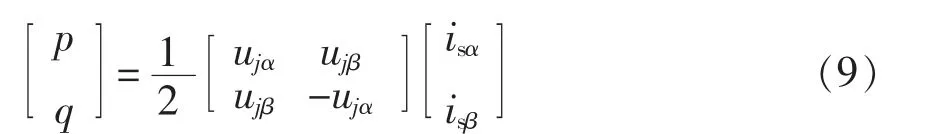
对式（9）求导得

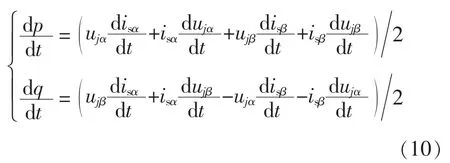
将式（7）和式（8）代入式（10），可得

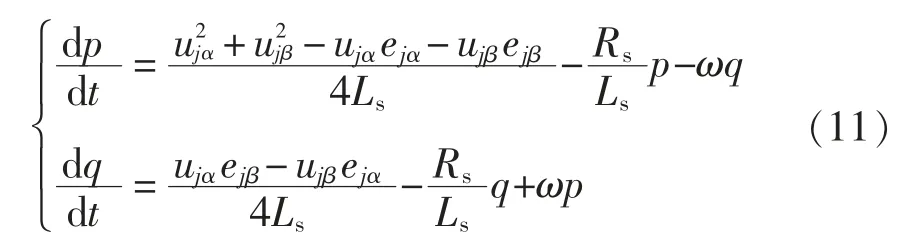
假设控制系统采样时间为T，第k 个采样周期有功和无功功率的变化量分别为Δp、Δq，有

由式（12）可得第k+1 个采样周期即t=（k+1）T时刻的有功和无功功率预测值，即

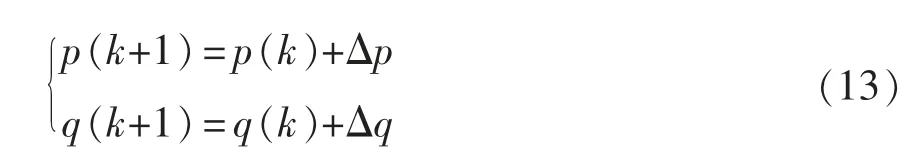
将式（11）和式（12）代入式（13），得

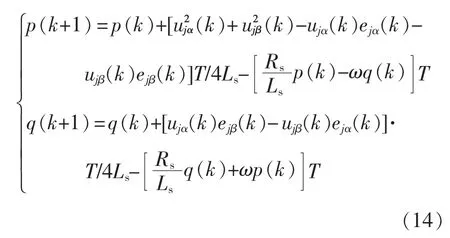
为了使SPH-MMC 两侧交流端口获得所期望的调制电压ej，同时根据模型预测原理，以每一个控制周期内有功、无功功率误差最小为原则，设计了优化性能目标函数为

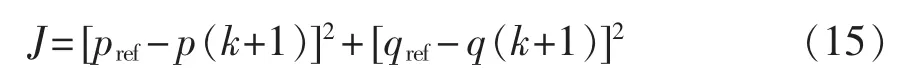
式中，pref、qref分别为期望的MMC-RPC 补偿有功功率和无功功率。

3.2 引入延时补偿控制

工程实际中控制器的采样、运算并不能瞬时完成，存在一个采样周期的延迟，即第k 个周期的SPH-MMC 交流端口电压采样值并不能够应用在当前的采样周期，而将应用在下一个采样周期即第k+1 个周期。即使延迟的时间很短，如果不对其进行补偿，将导致控制系统出现较大偏差，不能准确地对MMC-RPC 进行控制，无法获得很好的治理效果。所以，为了补偿采样周期延迟所带来的偏差，需要进行“两步预测”，即式（15）中的p（k+1）、q（k+1）相应改为p（k+2）、q（k+2），则式（15）改为

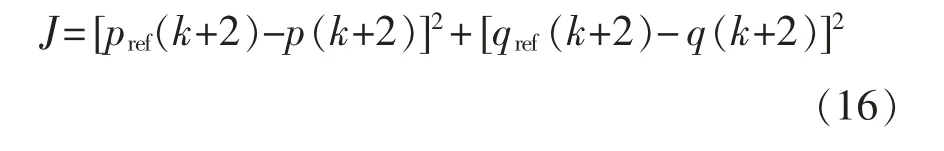
其中，p（k+2）、q（k+2）可由式（14）推导而得，即

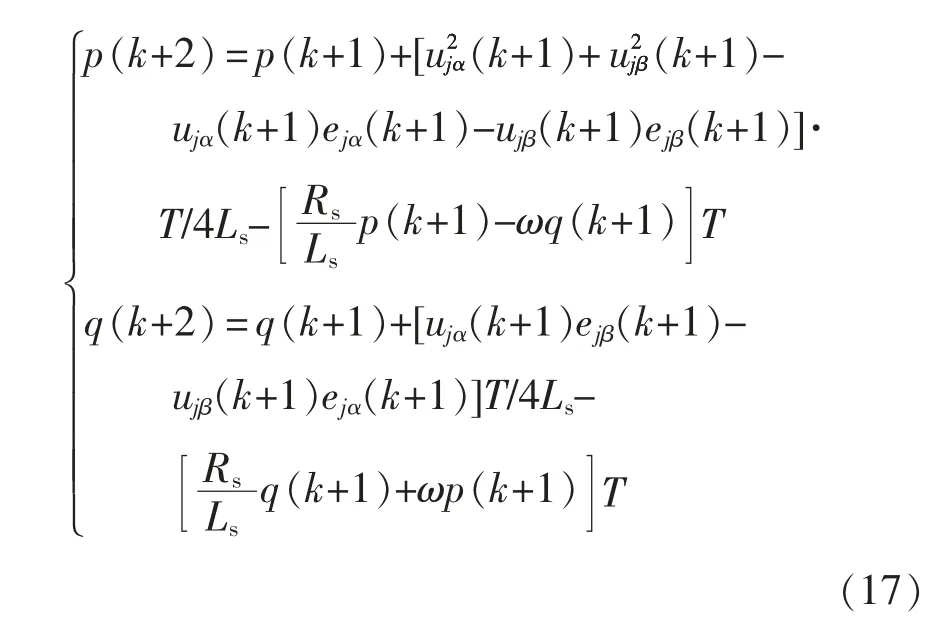
为了达到期望值与预测值之间的误差最小，即目标函数最小的控制目标，根据数学中的代数知识，需选择两侧供电臂交流端电压ejα、ejβ使目标函数最小，所以对式（16）分别求ejα、ejβ的偏导并令其为0，可得SPH-MMC 交流端口的电压最优值为

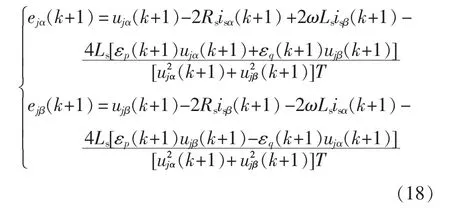
式中：εp（k+1）=pref（k+1）-p（k+1）；εq（k+1）=qref（k+1）-q（k+1），且变量均为（k+1）T 时刻的预测值。其中有功、无功的预测值p（k+1）、q（k+1）可由式（14）得到，其余变量可由二阶拉格朗日插值法得到[17]，以isα（k+1）为例，计算公式为

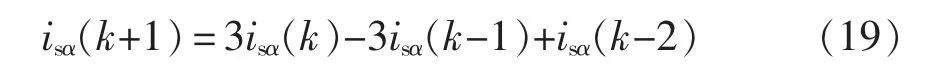
综上可得如图3 所示的控制系统总框图。电容电压排序算法指的是根据SPH-MMC 桥臂上电流的正负对子模块电容电压进行升/降序排列，确定SPH-MMC 桥臂上所投入的子模块数，进而控制SPH-MMC 的输出电压。

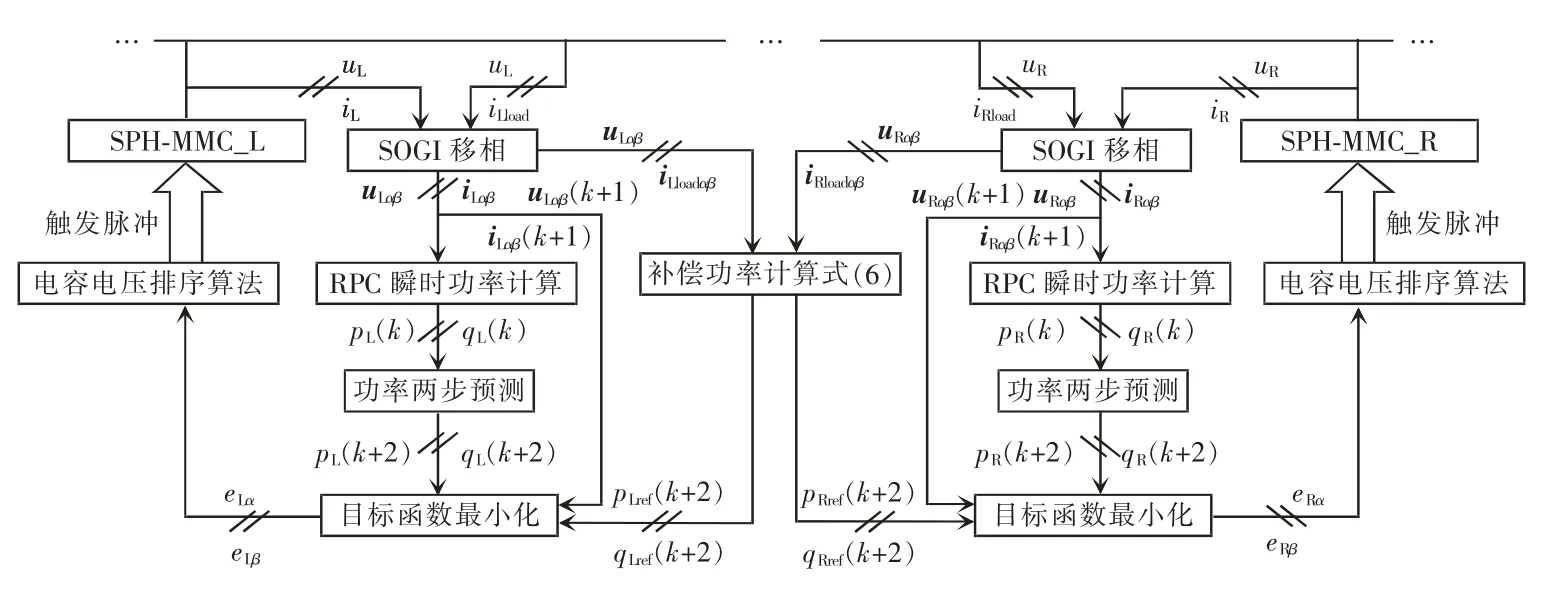
图3 基于MPDPC 的MMC-RPC 控制总框图Fig.3 Overall block diagram of MMC-RPC based on MPDPC

4 仿真分析

为了验证上述控制策略的有效性和优越的治理性能，根据图3 的控制框图在Matlab/Simulink 中分别搭建了基于MPDPC 控制、传统DPC 控制和双闭环PI 控制的MMC-RPC 模型，在同样仿真参数和工况下进行仿真对比。具体仿真参数见表1。

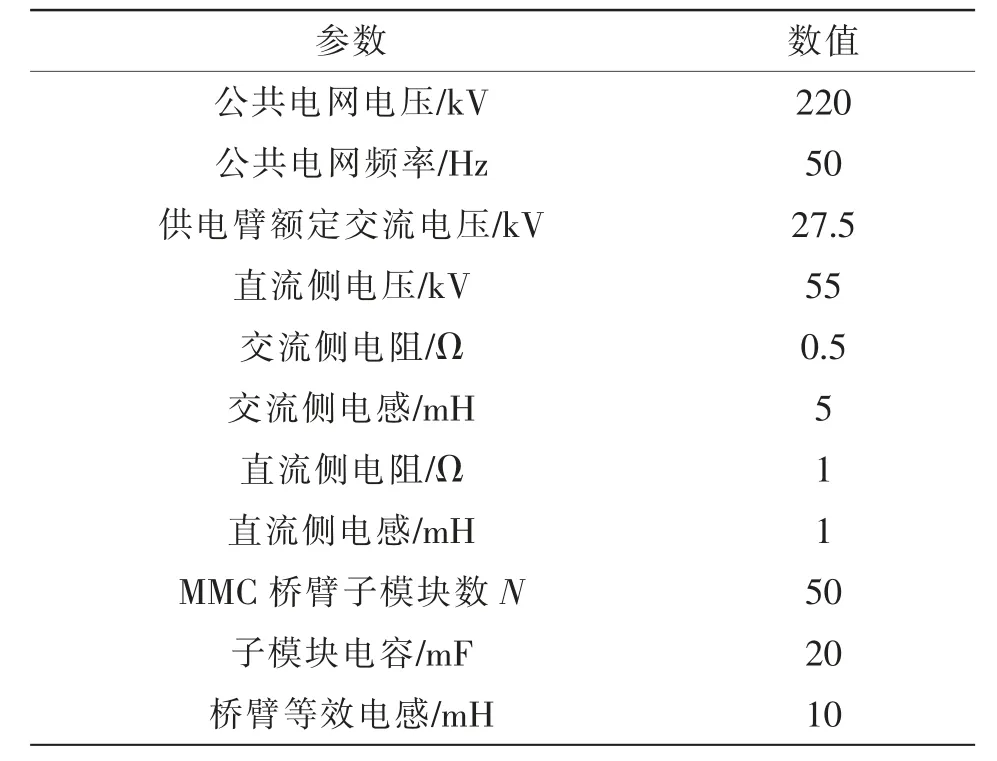
表1 具体仿真参数Tab.1 Specific simulation parameters

4.1 原边电流、直流侧电压、功率波形

为充分验证基于MPDPC 控制的MMC-RPC对牵引网电能质量的综合治理能力，模拟一种机车负载平衡度最差的情况，即左右两侧供电臂仅有一侧有机车运行。假设R 侧供电臂有一列有功功率为15 MW、无功功率为3 Mvar 的机车在运行，并且向牵引网注入3、5、7、9 次谐波，而L 侧无机车运行。为了体现MPDPC 控制的有效性和优越性，在仿真参数相同的情况下与DPC 控制和双闭环PI 控制的原边电流、直流侧电压、功率波形进行对比，在0.2 s 时投入MMC-RPC 对牵引网电能质量进行治理。

4.1.1 V/v 变压器原边电流波形

如图4 为3 种不同控制方式下MMC-RPC 治理前后的V/v 变压器原边电流波形对比。可以看出：投入MMC-RPC 治理前，原边电流存在负序分量和大量的谐波分量，三相电流严重不平衡；0.2 s时投入MMC-RPC，三相电流达到平衡，负序和谐波分量得以消除；相比于采用双闭环PI 控制，MPDPC控制和传统DPC 控制的响应速度更快，三相电流达到平衡状态的时间更短，且平衡度更高；而MPDPC 控制相比于传统DPC 控制稳定性更强，在MMC-RPC 投入瞬间电流几乎不产生波动，而且总谐波畸变率THD（total harmonic distortion）更低。

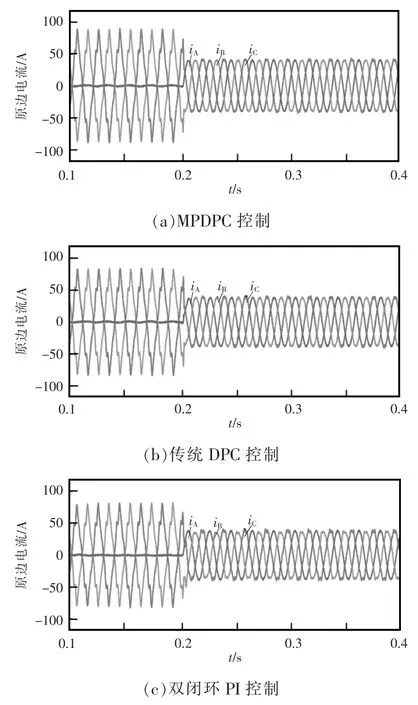
图4 3 种控制方式下的V/v 变压器原边电流Fig.4 Primary-side current of V/v transformer in three control modes

为对原边电流THD 进行分析，本文选取原边B 相电流。图5 为未投入MMC-RPC 治理前、双闭环PI 控制、传统DPC 控制以及MPDPC 控制下投入MMC-RPC 的B 相电流对比频谱分析，表2 为4 种情况下B 相电流各次谐波含量和THD 值的对比分析。可以看出，3 种方法均可对谐波进行较好的治理，但MPDPC 控制下的THD 更低。

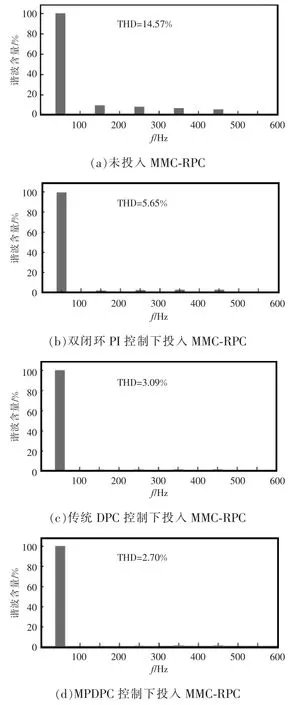
图5 B 相电流频谱图对比Fig.5 Comparison of phase-B current spectrum

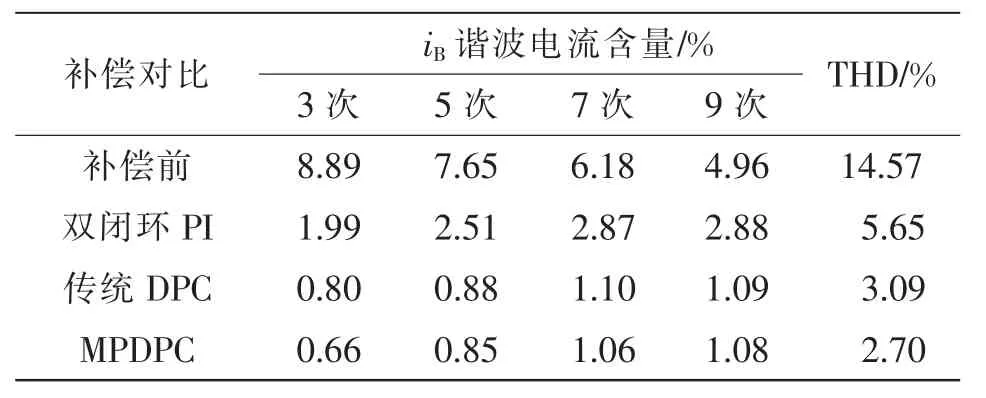
表2 MMC-RPC 补偿前后iB 各次谐波电流含量及THDTab.2 Harmonic current contents and THD of iB before and after MMC-RPC compensation

4.1.2 直流侧电压波形

由于文中所提MMC-RPC 是由2 个背靠背连接的SPH-MMC 组合而成，要求系统能够很好地控制直流侧电压，使其电压稳定。所以保持上述仿真工况不变，对比3 种控制方式下直流侧电压波形，如图6 所示。可见，3 种控制方法均能较好地实现直流侧电压的稳定控制；由其局部放大可见，相比双闭环PI 控制和传统DPC 控制，MPDPC 控制下的效果更好，直流侧电压波动相对较小，更好地保持系统可靠稳定运行。

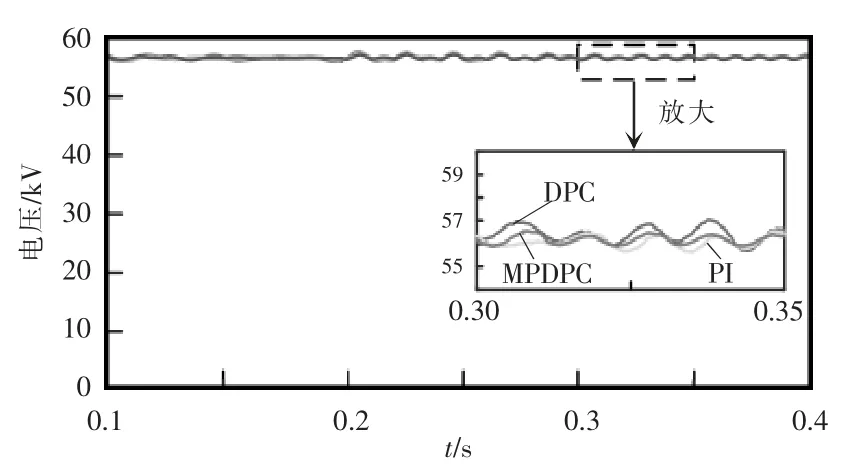
图6 3 种控制方法下直流侧电压波形对比Fig.6 Comparison of DC-side voltage waveform among three control methods

4.1.3 功率波形

保持上述仿真工况不变，对比3 种控制方式下MMC-RPC 补偿前后的左右两侧的总功率期望补偿值与实际输出功率，验证功率跟踪效果。本文以L侧供电臂为例，3 种控制方法下L 侧输出功率波形对比如图7 所示。可以看出，在3 种控制方式下，在0.2 s 投入MMC-RPC 后，L 侧输出功率均能较好地对功率期望值实现跟踪。将图7（a）（0.45～0.50 s）处的功率波形进行放大，如图7（b）、（c）所示，可以看出相比于双闭环PI 控制和传统DPC 控制，MPDPC控制下的MMC-RPC 输出功率更接近于功率期望值，跟踪效果更好，功率波动也相对较小，能够更精确地进行补偿。

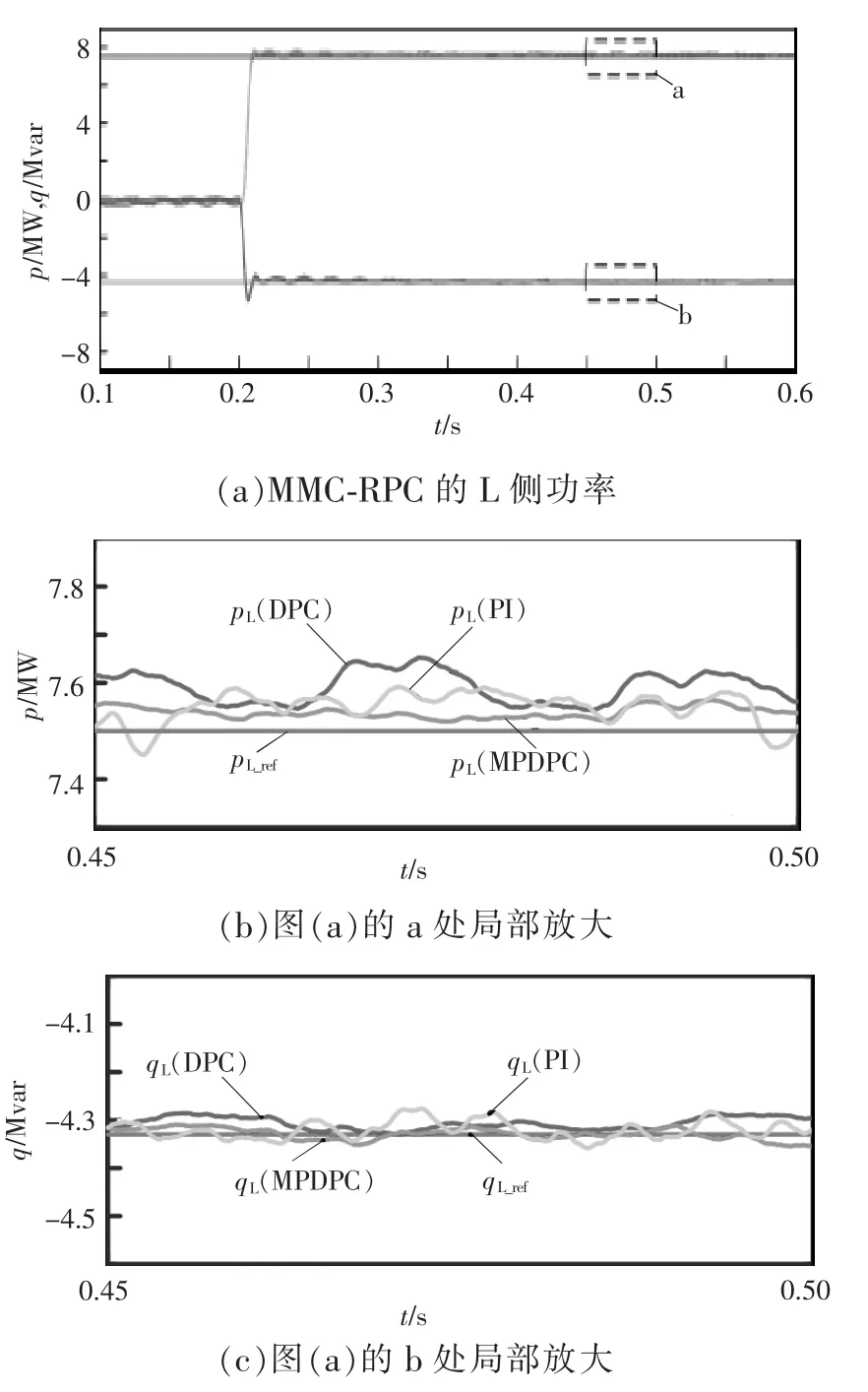
图7 3 种控制方法下L 侧输出功率波形对比Fig.7 Comparison of L-side output power waveform among three control methods

4.2 基于MPDPC 的MMC-RPC 仿真

为进一步验证MPDPC 控制下MMC-RPC 对牵引网的电能治理效果和补偿能力，模拟以下常见2种工况进行仿真。

（1）工况1：为验证MMC-RPC 在机车负载突变下的治理效果和补偿能力，假设已经投入MMCRPC 进行治理，且两侧供电臂仅有一侧有负载，0.3 s前R 侧供电臂有一列有功功率为15 MW、无功功率为3 Mvar 的机车在运行。0.3 s 时机车负载增加为有功功率25 MW、无功功率5 Mvar，0.4 s 后恢复为0.3 s 前的负载状态。

图8 为负载突变情况下V/v 变压器原边电流和两侧供电臂电流。可以看出，当0.3 s 负载突增时，原边电流和两侧供电臂电流随之增加，且很快到达平衡状态；0.4 s 恢复到之前的负载状态时，电流同样很快恢复到原来的平衡状态。可以看出在负载突变的情况下，MMC-RPC 能够在1/2 个周期内很快地对原边电流和两侧供电臂电流进行补偿，动态性能优越。

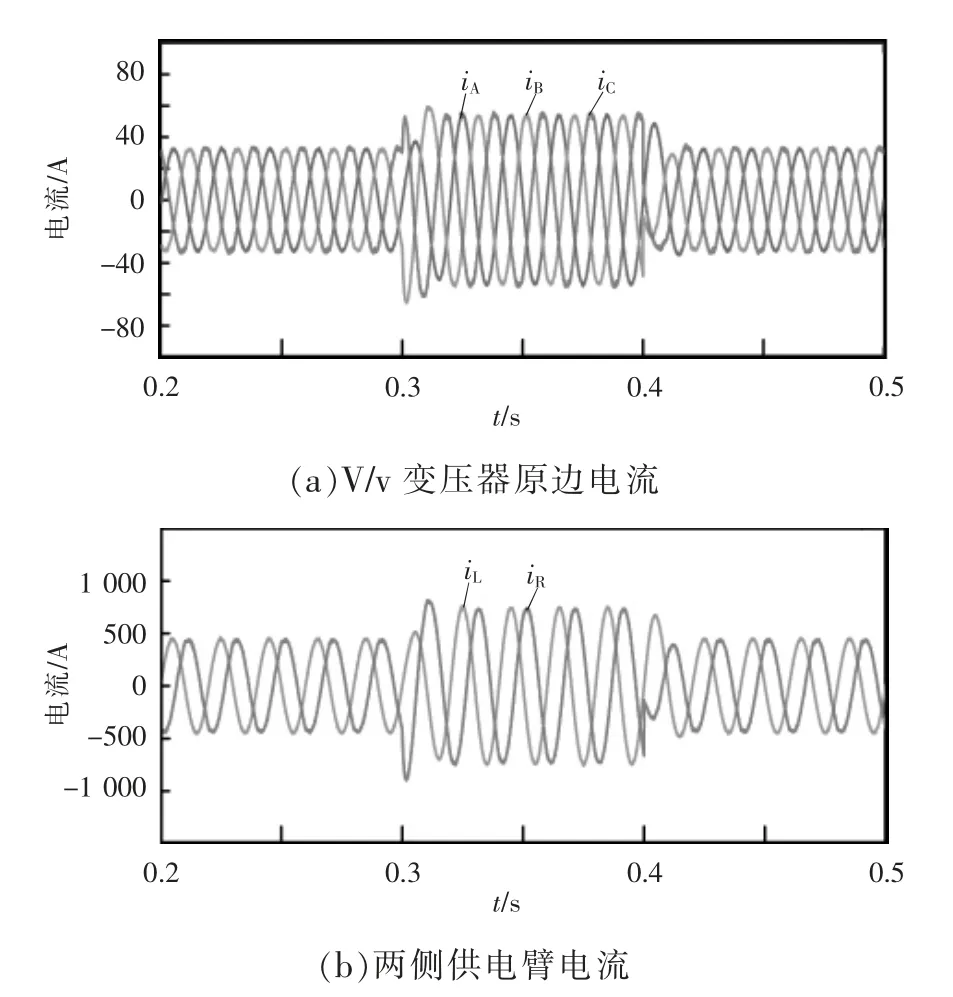
图8 工况1 下V/v 变压器原边和两侧供电臂电流Fig.8 Current on primary-side and side power supply arms of V/v transformer in Case 1

（2）工况2：为验证机车过分相情况下MMC-RPC的治理效果，假设已经投入MMC-RPC 进行治理，0.3 s 前有一列有功功率为15 MW、无功功率为3 Mvar 的机车在L 侧供电臂运行，0.3 s 时机车驶入分段换相区（供电死区），0.4 s 时进入R 侧供电臂区间。图9 为机车在过分相情况下V/v 变压器原边电流和两侧供电臂电流。可以看出通过MMC-RPC 的治理和补偿，机车发生过分相后原边电流很快恢复到之前的三相对称状态，两侧供电臂电流也很快地进入平衡状态，说明MMC-RPC 能够很好地应对机车负载过分相的情况。

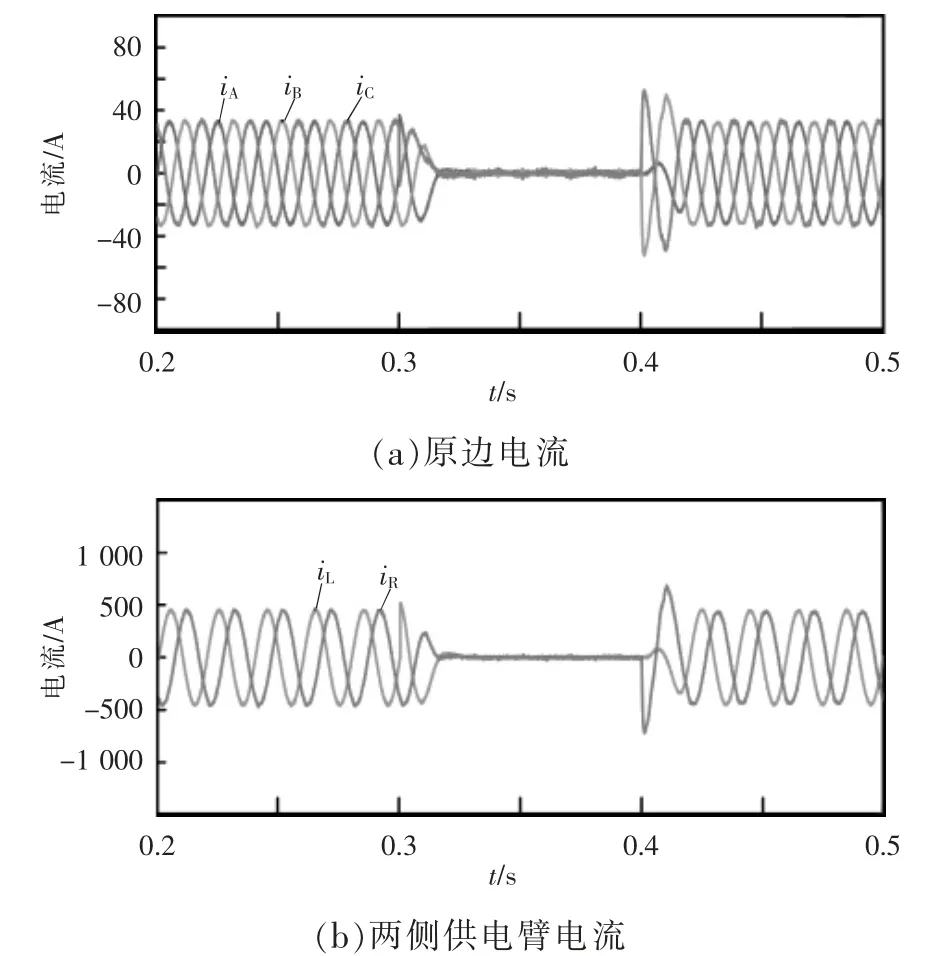
图9 工况2 下V/v 变压器原边和两侧供电臂电流Fig.9 Current on primary-side and side power supply arms of V/v transformer in Case 2

5 结论

基于模型预测控制理论，针对MMC-RPC 提出了一种新的直接功率控制策略，通过仿真分析得出以下结论：

（1）在同样的参数和工况下，对不同控制方法下的MMC-RPC 电能质量治理效果进行仿真验证，可以得出相比于双闭环PI 控制和传统DPC 控制，MPDPC 控制下的牵引变压器原边电流具有更低的THD，达到稳定平衡状态的时间更短，且能够更好地控制直流侧电压稳定，输出功率也更加精确地跟踪功率期望值，具有良好的动态性能。

（2）MPDPC控制下的MMC-RPC可有效消除机车运行产生的负序电流和谐波，使原边电流快速达到三相平衡，且能够有效应对机车负载突变和过分相的情况，响应速度较快，能够较好地对牵引供电系统的电能质量进行治理。