一种基于节点比较法的三相四桥臂并网逆变器模型预测控制方法

曹天旭，安浩澎，龙 波

（电子科技大学机械与电气工程学院，成都 611731）

并网逆变器作为把直流电能转化为高质量交流电能的桥梁，是基于可再生能源（如风能、太阳能）的分布式发电系统十分重要的一环[1-2]，它的控制也是系能源并网发电的重要研究课题。传统并网逆变器的结构为三相半桥逆变器，输出脉宽调制PWM（pulse-width-modulation）电压波形存在丰富的开关谐波。为了滤除大部分的谐波，在输出端接入LCL 型滤波器，使其输出波形满足谐波标准[3-4]。而低压配电网多采用三相四线制系统，需要通过三相四桥臂逆变器将分布式电源接入系统。

对于三相四桥臂并网逆变器的控制方法，比例-积分-微分PID（proportion-integral-derivative）控制器应用广，实现较为简单，但是存在固有稳态误差，且动态性能差[5]；比例-谐振PR（proportion-resonant）控制器的调节一般是采用电流外环的反馈，但对参数敏感，系统设计和参数选取十分复杂[6]。模型预测控制MPC（model predictive control），是近年来在电力电子系统控制中被广泛讨论的一种反馈控制策略[7]。在三相四桥臂逆变器的模型预测控制研究中，文献[8]研究了离网环境下LC 型三相四桥臂并网逆变器的模型预测控制；文献[9]在此基础上进一步研究了准Z 源以及不平衡负载条件下的有限控制集-模型预测控制FCS（finite-control-set）-MPC 策略；文献[10]在建立代价函数的基础上，采用了基于神经网络的约束MPC 求解输出占空比的最优解；文献[11]采用李雅普诺夫模型预测控制，对三相四桥臂逆变器的跟踪误差、谐波失真THD（total harmonic distortion）和计算量进行了综合考量。在三相四桥臂LCL型并网逆变器中，模型预测控制可以综合考虑输出跟踪误差、THD 和开关损耗这3 个因素，以未来几次的开关序列作为变量，通过权重分配构建代价函数，求解代价函数最小时的开关序列，并应用第1个开关序列作为逆变器的控制序列，不需要进行PWM。若权重分配合理，预测时域更长，MPC 控制策略可以最大限度地兼顾到被控制量，进行稳态动态性能更好的控制。但是长预测时域会给计算机或微处理器带来很大的计算量，加重系统负担。因此，本文介绍一种球形译码算法，可以大幅度减小计算量。同时，球形译码的计算量和初始半径的选取也有很大的关系，文献[12]采用了Babai 估计确定初始半径，可以缩减计算量。本文引入了一种新型的方法——节点比较法，可以进一步缩小初始半径，使计算时间更小。

本文首先分析了三相四桥臂LCL 型并网逆变器拓扑结构，并构建了其精确数学模型；综合考虑谐波失真、跟踪误差和开关损耗3 个主要因素，构造了代价函数，并通过球形译码减小了运算量；最后通过Matlab 进行了仿真，确定了控制的权重参数和预测时域，仿真结果验证了控制算法的理论正确。

1 系统建模

三相四桥臂LCL 型并网逆变器的拓扑结构如图1 所示，直流电源电压VD经三相四桥臂半桥逆变器后，由LCL 型滤波器滤波，最终馈入三相交流电网电压vga、vgb、vgc。逆变器侧电感L1、网侧电感L2以及滤波电容C 的支路上均串有电阻R1、R2、RC；中性线与逆变器的第4 桥臂相连，并串有电感Ln。i1a、i1b、i1c为逆变器侧电流，i2a、i2b、i2c为网侧电流，vCa、vCb、vCc为电容电压，in为中性线电流。

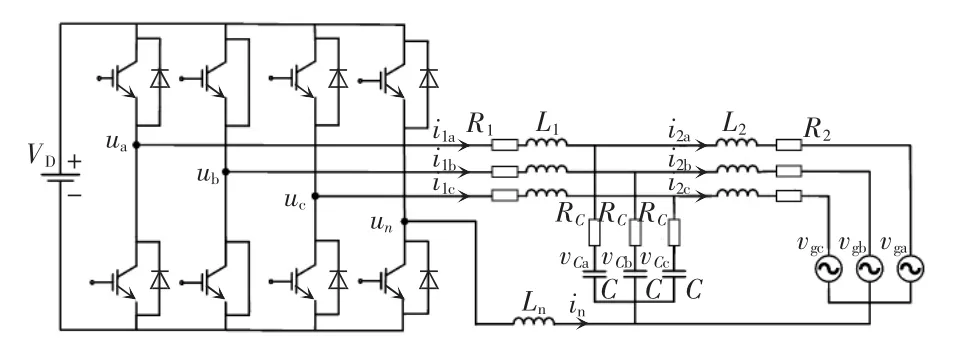
图1 三相四桥臂LCL 型并网逆变器拓扑结构Fig.1 Topology of three-phase four-leg LCL-type gridconnected inverter

首先，定义三相矢量为

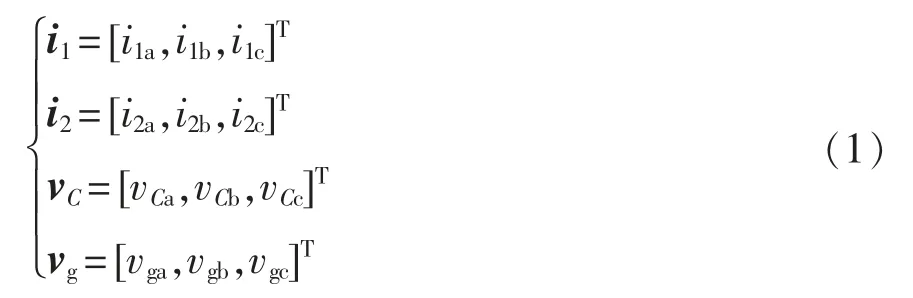
设u 代表每个桥臂上管子的开关状态，其中：1代表上桥臂导通，下桥臂关断；-1 代表下桥臂导通，上桥臂关断。那么

其中，ua、ub、uc、un∈{-1，1}。

根据基尔霍夫定律，可以推导出三相四桥臂并网逆变器的电路方程为

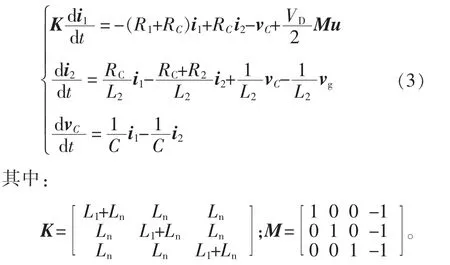
选取系统的状态变量x 为

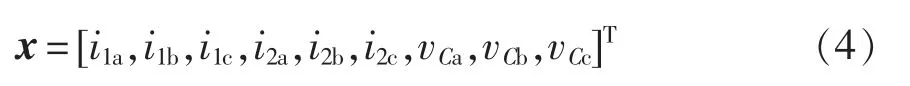
根据x 建立状态空间方程为

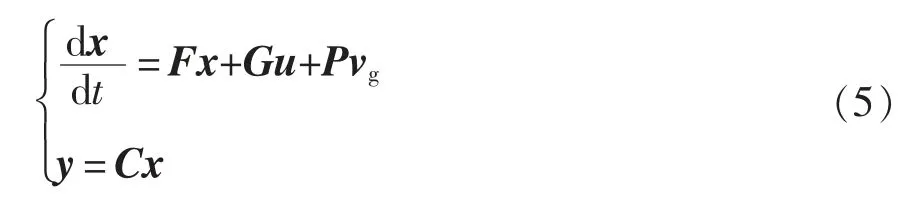
式中：F、G、P 为电路的参数矩阵；y 为输出变量，是状态变量x 的权重再分配；C 为分配系数矩阵，即

式中，λ1、λ2和λ3分别为逆变器侧电流i1、电网侧电流i2和电容电压vC的权重因子。

用Du Hamel 公式[13]将式（5）离散化，得到电路在离散时间域的状态空间方程为

由于k 时刻x（k）和vg（k）为可测得的已知量，那么根据电路的离散化状态空间方程式（7），就可以递推出x（k+m）和y（k+m），其中m=0，1，…，N，N为预测时域，则有

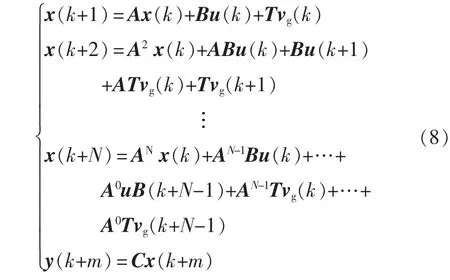
式（8）通过k 时刻的状态变量采样值预测出了k+N时刻的状态变量。

根据上述关系，设Vg（k）=，其中：Y（k ）为输出向量，合并了未来N 个时刻的输出，它们只由k 时刻的输入x（k）递推得到；U（k）为N 个时刻要采用的开关序列的合并，模型预测控制就是要求出这个序列的最优解，并把它的第1 组开关序列应用于逆变器中；Vg（k）为N 个时刻的电网电压，它自从k 时刻被测取出来后，因为不考虑电网电压的波动，所以在未来时刻都是确定的。

在k，k+1，…，k+N-1 时刻，根据递推关系，可以推出每一时刻的状态空间方程。把这些方程按照式（8）中的向量进行整合，可以得到考虑了预测时域N 的系统离散化输出方程，即

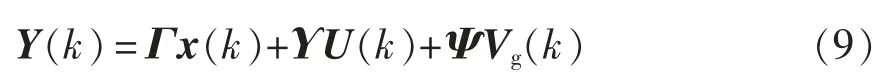
式中，Γ、Υ、Ψ 为关于A、B、C、T 的矩阵，均为时不变矩阵。

2 三相四桥臂逆变器的模型预测控制

2.1 代价函数的建立

三相四桥臂LCL 型并网逆变器要实现的最终目的是并网电流的波形符合要求，稳态时并网电流要有较小的跟踪误差，较小的谐波失真；动态响应要有较小的超调量，快速跟踪指令。除了对并网电流的要求之外，还需考虑系统的开关损耗。

在考虑了上述因素后，设计代价函数为

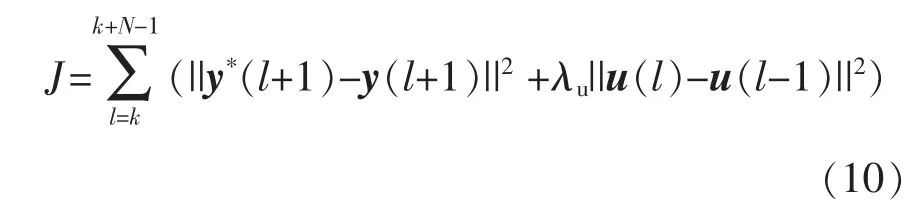
式中：||·||代表向量的欧式二范数；y*为输出参考值，由于电路的参数稳定，第k～k+N-1 时刻的y*也是确定的；λu为开关损耗的权重因子。代价函数的第1 项是输出参考值与实际值之差，考虑了跟踪误差和谐波失真；第2 项是开关状态的变化量，考虑了开关损耗。

把式（9）代入式（10）中，可以得到

式中：Y*（k）为与Y（k）相对应的N 个时刻合并的参考向量，Y*（k）=；u（k-1）第k-1 时刻的开关状态；S 和E 为时不变矩阵。

通过代价函数式（11），若实现最优的控制效果，需要代价函数最小，这时对应的U（k）即为最佳的开关序列，即

采取Uopt（k）的第1 组开关状态作为开关输入，就完成了模型预测控制的闭环控制。

进一步计算，需把代价函数进行拆分后再合并，经过整理得

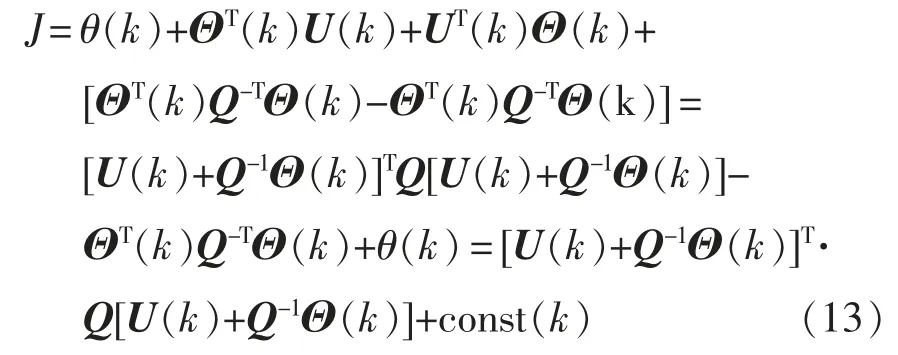
式中：const（k）是一个常数，在每个采样时刻都是确定量，所以求代价函数最小值时，不需考虑const（k），故以下的J 不再含有此项；Θ（k）为系统的参数矩阵；Q 为对称正定矩阵，经过柯列斯基分解后，可以变为

其中，H 为4N×4N 的下三角矩阵。所以有

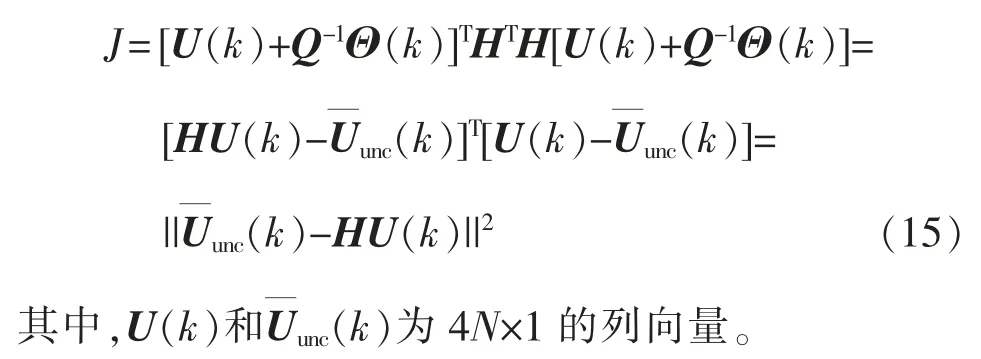
2.2 基于节点比较法的球形译码

球形译码是一种广泛应用于信号检测的最大似然检测方法。通过设定一个以接受向量为中心的超球，仅搜索超球内的格点来找到最大似然解，从而避免了繁琐复杂的搜索。球形解码算法的树形搜索过程中，有2 种搜索策略，分别是FP（Fincke-Phost）策略[14]和ER（Schnorr-Euchner）策略[15]，本文采用FP 策略。

U（k）是4N×1 的列向量，每个元只有1 和-1两种情况，则U（k）有24N种情况，每一种情况都对应一个代价函数J，所以代价函数[16]可以表示为

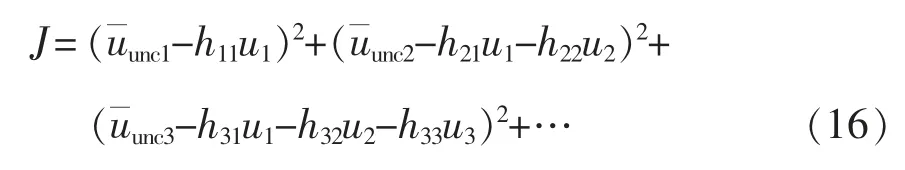
此时的代价函数是由4N 个平方项之和构成的。由于U（k）的每一个元即ui（i=1，2，…，4N）都存在-1和1 两种取值，则代价函数可以用二叉树的形式来展现。

如图2 所示，以三层的二叉树为例，说明球形译码的原理。用每一条线段代表代价函数的其中一个平方项，那么从根节点开始一直到某个叶子节点，所经过的线段长度之和，就是代价函数值。穷举搜索可以求出每种情况对应的代价函数值，再加以比较，但是消耗大量的计算时间。球形译码首先会设置一个初始半径d0，之后从左至右，逐层向下计算，判断累计半径平方和是否小于初始半径平方，黑色球节点部分为采用的路径，灰色球节点则未被采用。当（u1，u2，u3）=（1，1，1）时，累计半径之和大于初始半径，不被采用；当（u1，u2，u3）=（1，1，-1）时，累计半径之和小于初始半径，初始半径更新为此累计半径，同时返回上一层继续上述运算。如此计算，最后得到最佳的（u1，u2，u3）=（-1，1，1）。

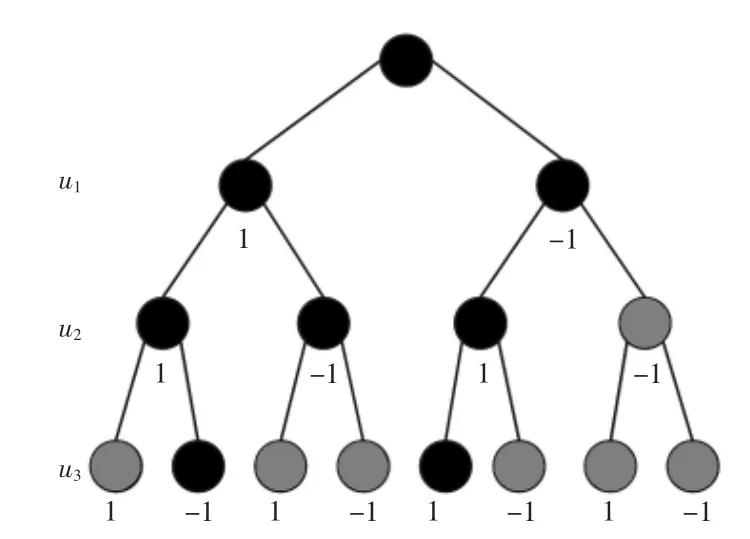
图2 球形译码算法的树形搜索结构Fig.2 Tree search structure of sphere decoding algorithm

初始半径d0对减小球形译码的计算量有重要作用，既不能太大，以至于起不到减小计算量的作用；也不能太小，以至于最优解也被剔除。

在本文中，采用了节点比较法来估计初始半径d0，其流程如图3 所示。节点比较法的思路为：将搜索树的每个节点对应的2 条路径长度进行比较，取结果较小的支路，并继续比较支路节点的2 条路径长度。以此类推，并将路径长度叠加。最后得到的总路径长度设置为初始半径。节点比较法本身得到的就是一个次优解（或最优解），所以初始半径不可能小到球形译码会把真正的最优解排除。相比于Babai估计，节点比较法的计算量可以得到进一步减少。

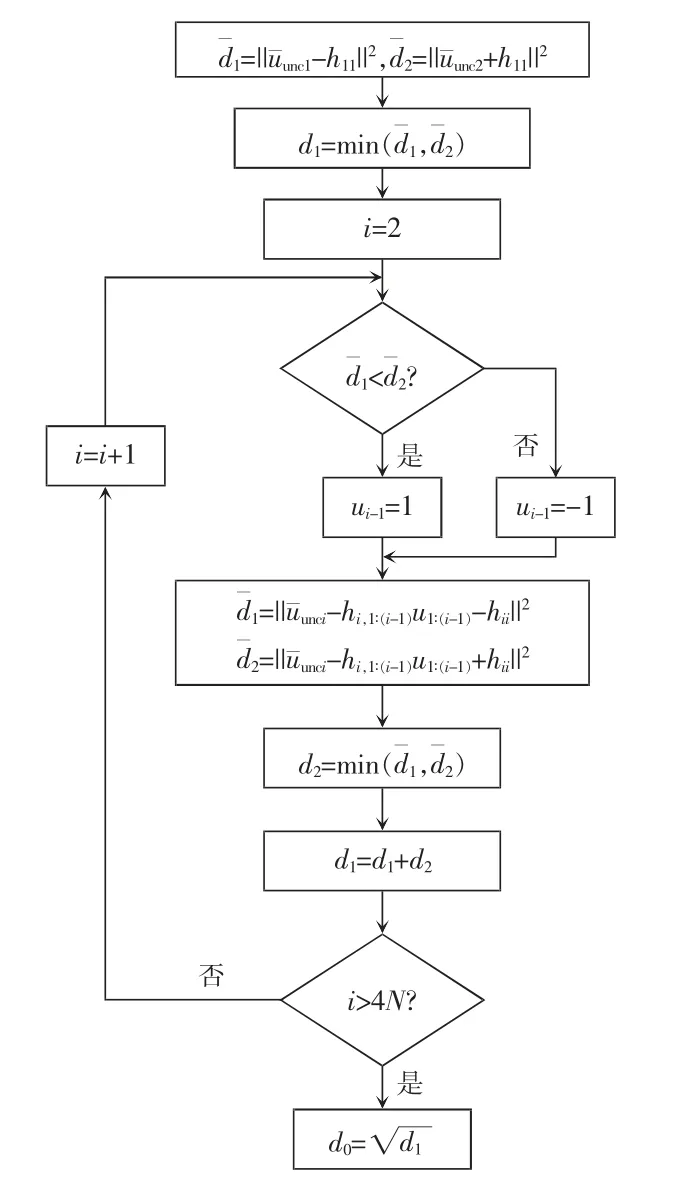
图3 节点比较法流程Fig.3 Flow chart of node comparison method

设最优解为Uopt（k），则有

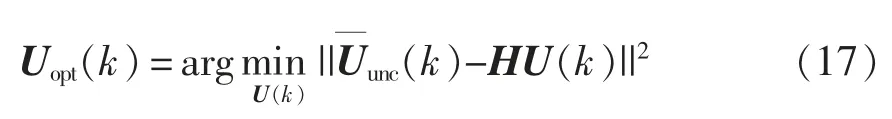
当每个采样时刻的初始半径ρini（k）用节点比较法确定后，根据球形译码的原理，执行以下算法。

算法1球形译码。算法如下。

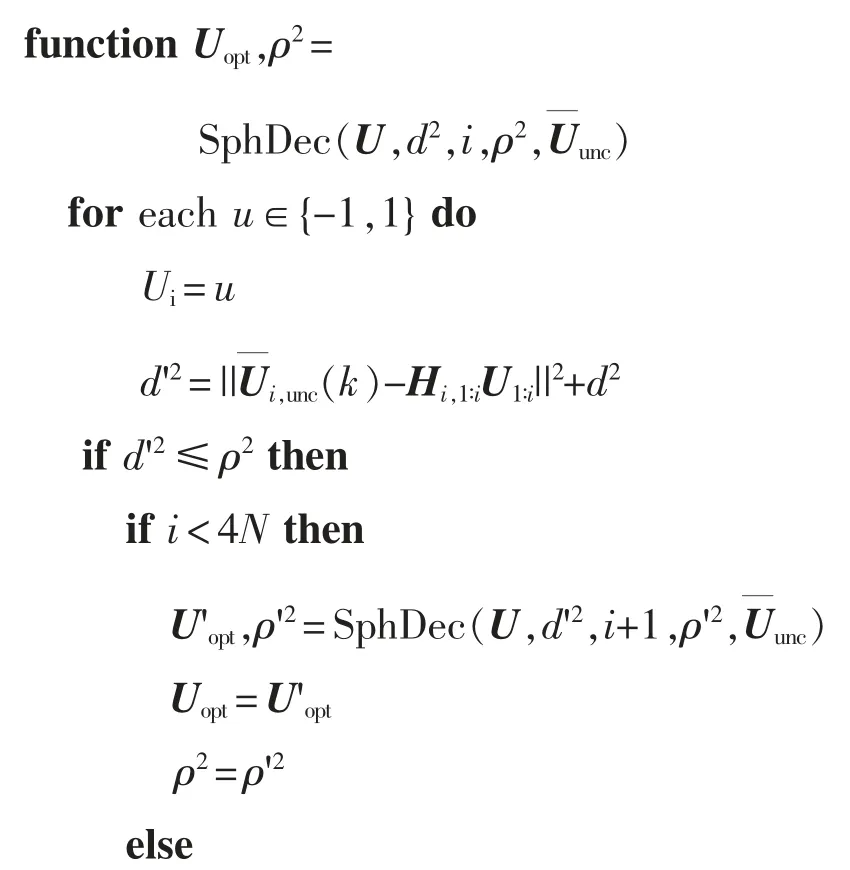
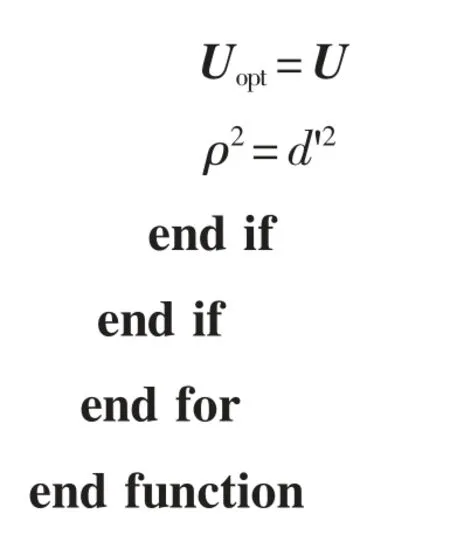
即可实现三相四桥臂LCL 型并网逆变器的模型预测控制。此算法会生成Uopt（k），即当前时刻的最优开关序列。采用此序列的第1 组开关量作为驱动信号，反馈到逆变器中。综合上述分析，最终的系统控制框图如图4 所示。

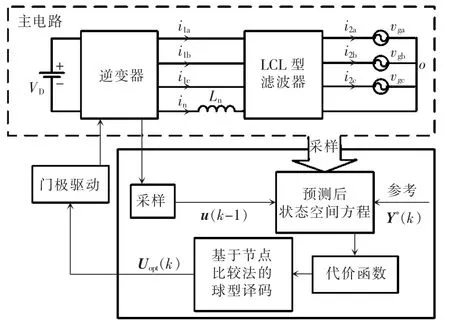
图4 三相LCL 型并网逆变器的模型预测控制框图Fig.4 Block diagram of three-phase LCL-type gridconnected inverter under MPC

3 仿真分析

在Matlab 中建立了三相四桥臂LCL 型并网逆变器的模型预测-球形译码控制策略的数学模型，通过仿真实验对控制系统进行评估。选取λ1=λ2=1，λ3=0.1。

3.1 参数的选取

系统参数如表1 所示。

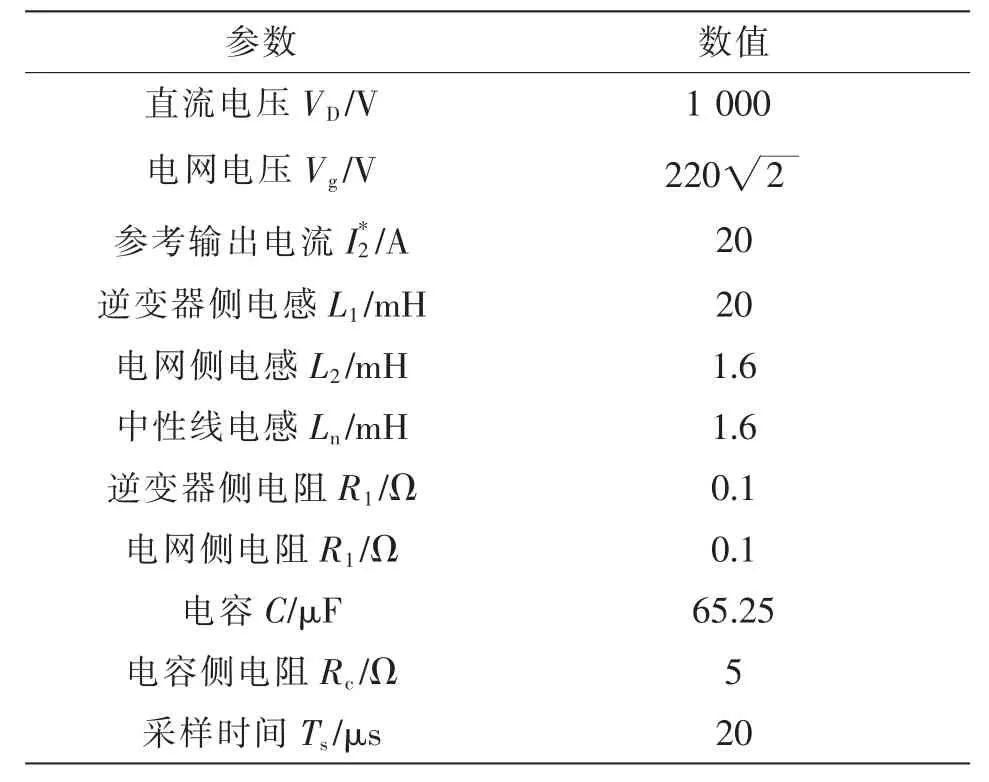
表1 系统参数Tab.1 System parameters

为了说明权重因子λu对系统稳态性能的影响，维持预测时域N=4 不变。图5 展示了λu对总谐波失真、跟踪误差和开关频率的影响。随着λu的增加，代价函数中开关损耗所占的权重越来越大，这会使开关频率降低，但是谐波失真和跟踪误差会有所增大。当λu≤10-2时，λu对减小开关损耗几乎不起作用；当10-2≤λu≤1 时可以起到平衡开关损耗和并网电流的质量的作用。因此，最终选取λu=0.1。

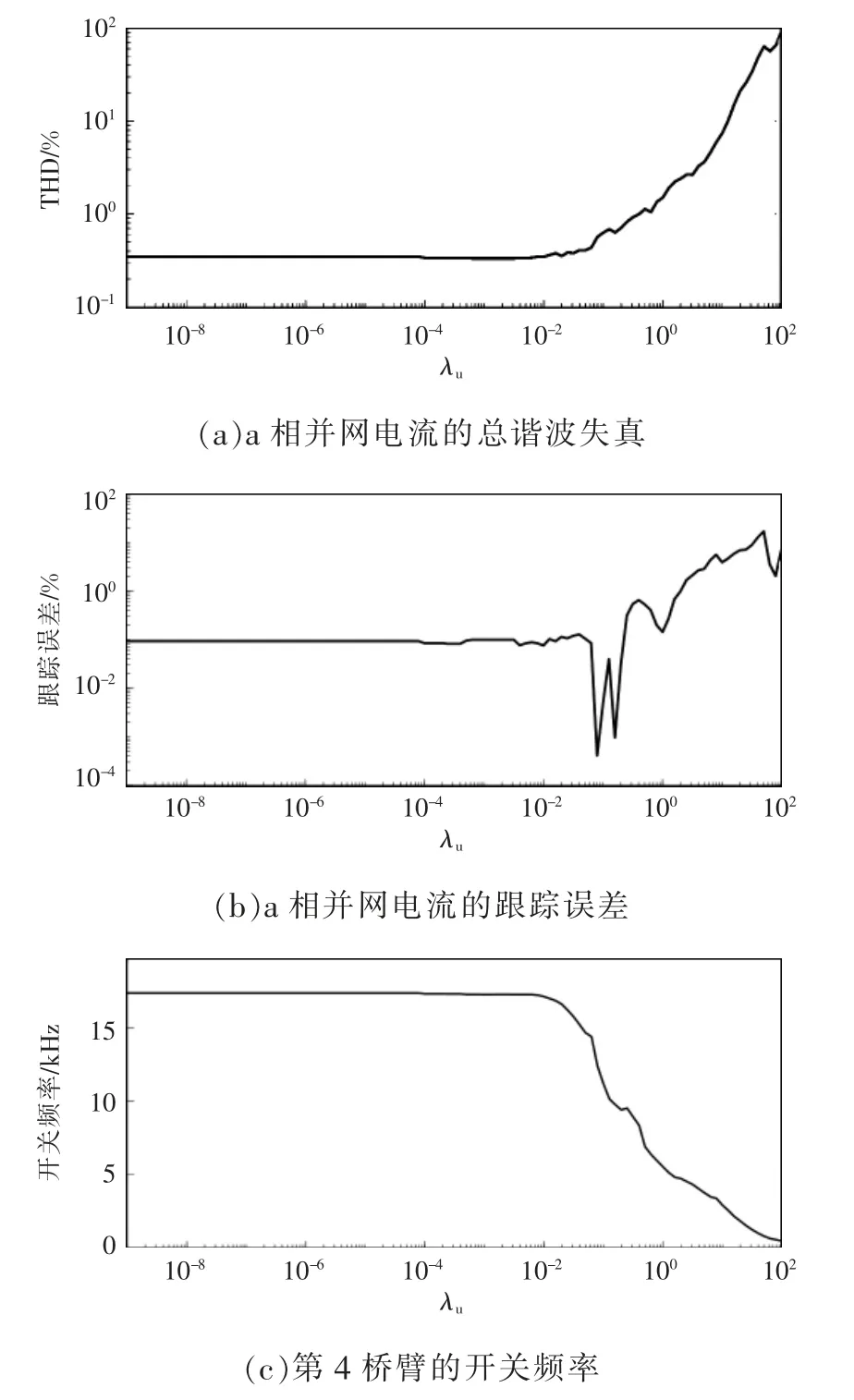
图5 N=4 时总谐波失真、跟踪误差、开关频率随权重参数λu 的变化Fig.5 Changes in THD,tracking error,and switching frequency with the adjustment of weighting coefficient λu when N is equal to 4

为了说明预测时域N 对系统稳态性能的影响，维持权重因子λu=0.1 不变。图6 展示了预测时域N对总谐波失真、跟踪误差和开关频率的影响。随着N 的增加，总谐波失真和跟踪误差呈现上下波动的趋势，开关频率呈现减小的趋势。但考虑到计算量会随着N 的增加而增加，当N>6 时，系统的仿真结果与N=6 时相比并没有得到很明显的改善，而计算时间还要大幅度提高。因此，最终选取N=6。

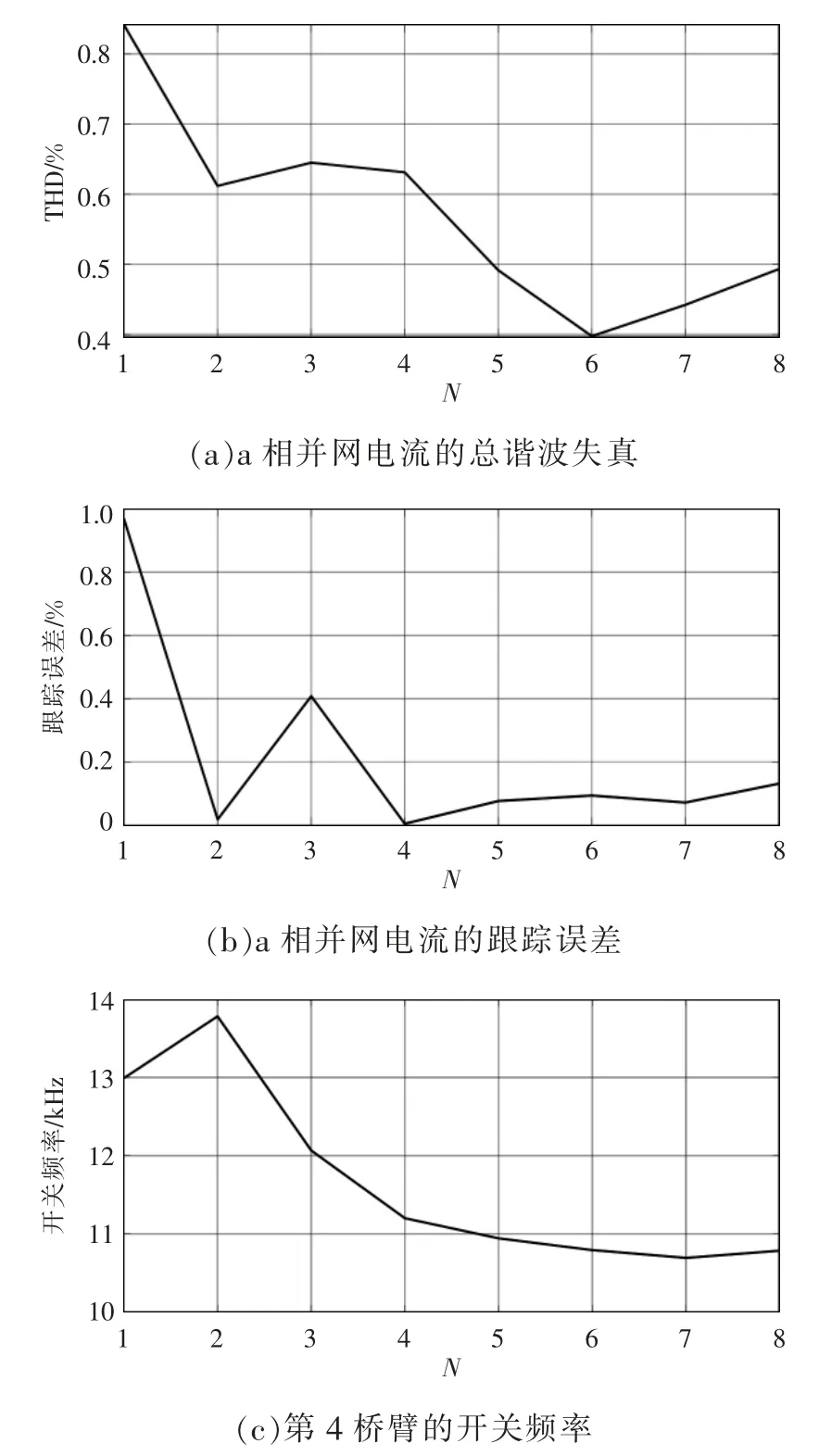
图6 λu=0.1 时的总谐波失真、跟踪误差、开关频率随预测时域N 的变化Fig.6 Changes in THD,tracking error,and switching frequency with the adjustment of prediction horizon N when λu is equal to 0.1

3.2 初始半径的选取方法

图7 显示了节点比较法和估计法在初始半径选取上的区别。在λu=0.1、N=6 的情况下，节点比较法的初始半径在2.0 附近，而Babai 估计法的初始半径在5.5 附近。节点比较法初始半径的更小，可以让球形译码排除更多次优解，减少计算量。图8显示了2 种方法随着预测时域的增加所消耗的计算时间。相比Babai 估计法，节点比较法的仿真时间减小了37.23%。

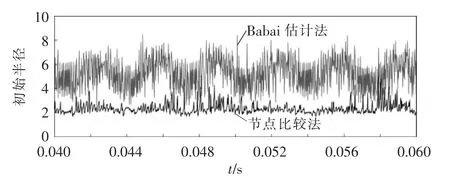
图7 节点比较法和Babai 估计的初始半径选取Fig.7 Selection of initial radius when using node comparison method and Babai estimation

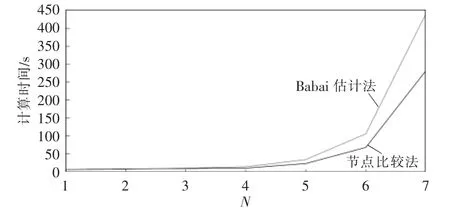
图8 节点比较法和Babai 估计法在不同预测时域中的计算时间Fig.8 Calculation time of node comparison method and Babai estimation in different prediction horizons

3.3 稳态响应

选取λu=0.1、N=6，图9 展示了并网电流的稳态波形和谐波频谱，逆变器并网电流THD=0.397%，跟踪误差为0.093%。仿真结果证明了模型预测控制的优秀性能，并网电流总谐波畸变率很小，符合入网标准。

图10 展示了稳态时4 个桥臂的开关时序，由式（3）的第1 个方程可知，第4 桥臂的开关状态un与abc 三相的开关状态ua、ub、uc都有关，这是由于中性线电流in是三相逆变器侧电流的叠加，因此第1 个方程的逆变器侧电流存在耦合关系，而第4 桥臂控制的是中性点电压，因此un的开关频率应该是最大的，图9 也证明了这一点，即a 相、b 相、c 相和第4 桥臂的开关频率分别为4.875、4.692、4.958 和10.792 kHz。提高权重因子λu，在并网电流符合入网标准的前提下，第4 桥臂的开关频率最多可以降低到约1 kHz。

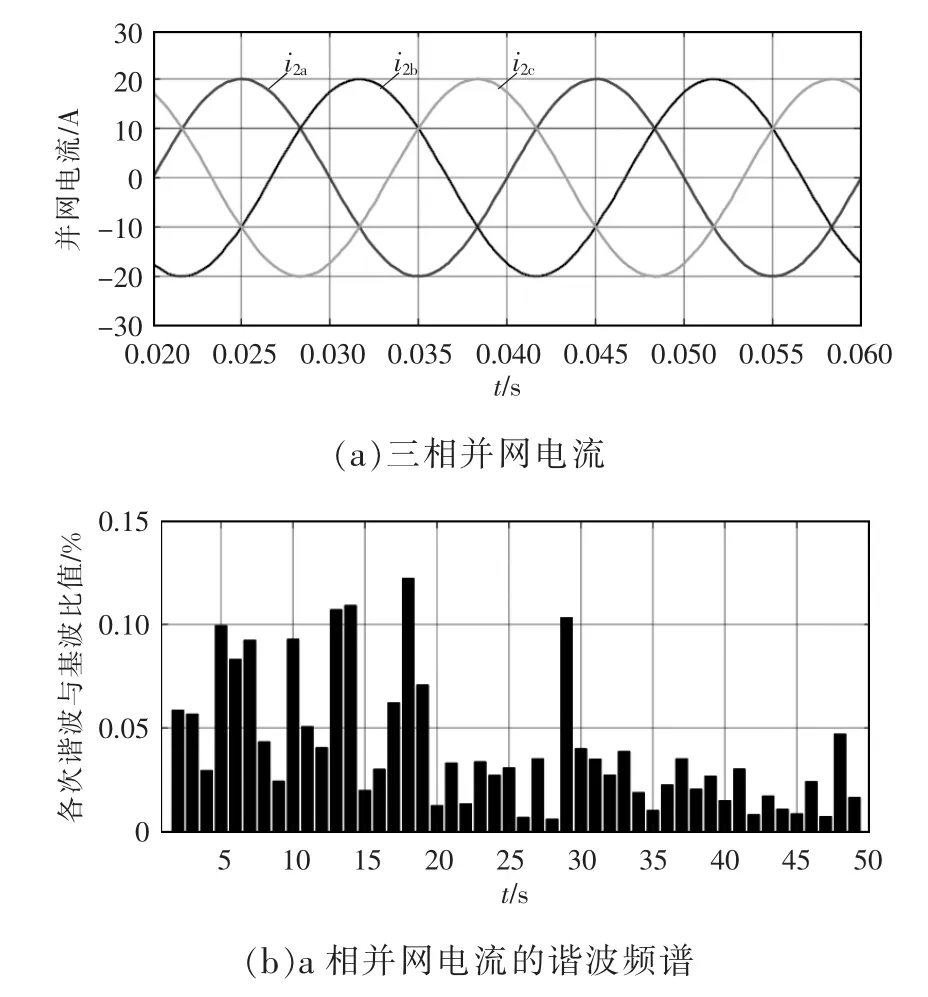
图9 稳态并网电流及谐波频谱Fig.9 Steady-state grid-connected current and harmonic spectrum

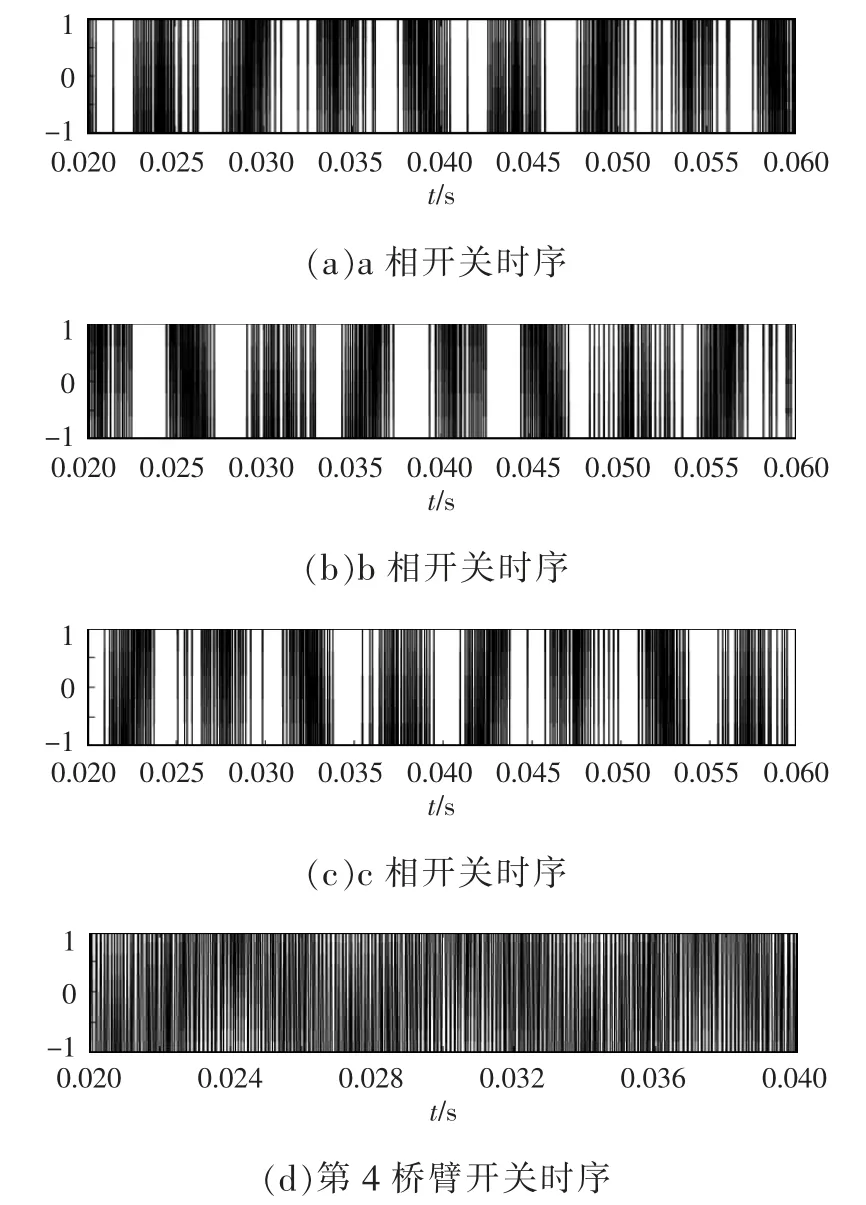
图10 开关时序Fig.10 Switching sequence

3.4 动态响应

选取λu=0.1、N=6，图11 展示了a 相网侧电流骤升和骤降时的动态响应。a 相网侧参考输出电流在t=0.026 s 从20 A 突变为5 A 以及在t=0.026 s 从5 A 突变为20 A 时，动态响应时间均小于3 ms。仿真证明了模型预测控制在这种大幅度电流升降中能保持良好的动态响应，超调量小，调节时间短。

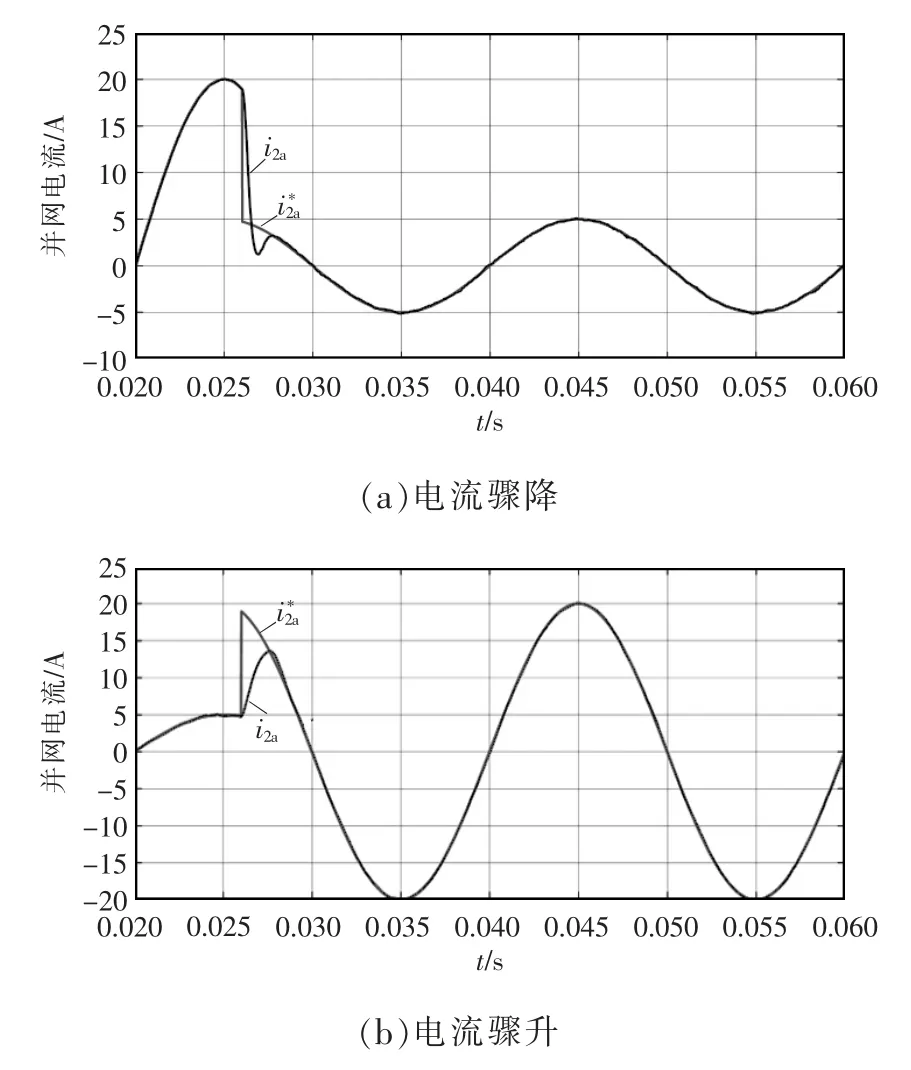
图11 并网电流的动态响应Fig.11 Dynamic response of grid-connected current

4 结语

对于三相四桥臂LCL 型并网逆变器的控制，模型预测控制是一种控制手段相对简单，控制效果出色，但是计算量大的方法。如果将代价函数J 转化为球形译码算法的标准形式，就可以运用球形译码来减少模型预测控制的计算量，从而达到更高精度的控制。经过仿真分析，证明了模型预测控制的稳态响应和动态响应可以满足要求，开关损耗也不是很高。同时，仿真分析比较了节点比较法和Babai估计的初始半径和计算时间，证明了节点比较法的初始半径明显更小，可以排除更多次优解，计算时间进一步减小。