基于盖尔圆定理的三相并网逆变器系统稳定判据及稳定性分析

谢玲玲，何方正，孙昌茂

（广西大学电气工程学院，南宁 530000）

随着新能源发电技术逐步成熟，发展可再生能源已经成为缓解能源危机的一种有效途径。并网逆变器作为风电、光伏等可再生能源接入电网的主要功率接口，在电力系统中得到了越来越广泛的应用[1]。并网逆变器与电网在公共耦合点PCC（point of common coupling）处相连，从PCC 看向电网，存在较长的输配电线路，使电网呈现阻感性的电网阻抗[2-3]，逆变器阻抗与电网阻抗的相互作用可能引起谐波振荡[4]，过高的电网阻抗可能导致并网逆变器系统失稳[5]。为了控制逆变器向电网输送的功率，需要利用锁相环PLL（phase-locked loop）来保证逆变器的输出电流与电网电压同步，但锁相环带宽的增加对并网逆变器系统的稳定存在负面影响[6]。近年来，世界各地发生了多起与可再生能源并网相关的振荡问题，为电力系统安全稳定运行提出了新的挑战。

针对并网逆变器系统的稳定性问题，国内外学者提出了基于逆变器小信号阻抗的稳定性分析方法[7-8]，将逆变器与电网视作两个独立的子系统来进行小信号阻抗建模，再通过广义Nyquist 稳定判据来分析系统稳定性。根据建立阻抗模型所使用参考坐标系的不同，小信号阻抗建模又可以分为两类：第1 类是谐波线性化方法，在静止坐标系下建立正负序阻抗模型[9-10]；第2 类是dq 小信号建模方法，在以电网频率同步旋转的dq 坐标系下建立阻抗模型[11-13]。逆变器的滤波器及控制回路会影响逆变器的小信号阻抗特性，文献[14]考虑逆变器控制回路中锁相环的影响，建立了LCL 型并网逆变器的阻抗模型，但没有考虑控制回路中的解耦反馈与电容电流反馈可能带来的影响。应用广义Nyquist判据分析系统稳定性时，需要求出系统回比矩阵特征值的频率响应[15-16]，由于逆变器的阻抗模型表达式较为复杂，故传统广义Nyquist 判据需要的计算量较高，降低了该方法在工程中的实用性。

本文同时考虑了锁相环和在电流环中加入解耦反馈与电容电流反馈对逆变器阻抗特性的影响，建立了dq 坐标系下的并网逆变器小信号阻抗模型，提高了模型的精度，更符合工程实际。在此基础上，根据广义Nyquist 判据提出一种改进的并网逆变器系统稳定性判据，通过盖尔圆定理估计系统回比矩阵特征值的位置，避免了直接计算回比矩阵特征值，大大减小了计算量，最后通过仿真与实验验证了该判据的有效性。

1 LCL 型并网逆变器的小信号模型

三相LCL 型并网逆变器系统结构如图1 所示。图中：S1～S6为开关管，L1和L2分别为变换器和电网电感，和RC分别为L1、L2和C 的寄生电阻，Zg和Zinv分别为电网阻抗和逆变器阻抗，ug为电网电压，uPCC为公共耦合点电压，uC为滤波电容电压，uinv为逆变器交流侧出口电压，Udc为直流侧电压。控制回路中，解耦反馈系数ω0LT=ω0（L1+L2），ω0为电网基频角频率，KC为电容电流反馈系数，Gi为电流环PI 控制器。

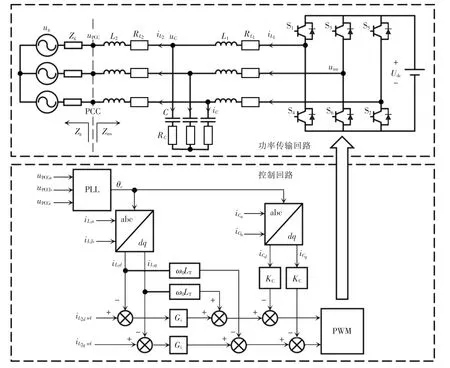
图1 三相LCL 型并网逆变器系统结构Fig.1 Structure of three-phase LCL-type grid-connected inverter system

在弱电网条件下，PCC 电压会出现扰动，这会使得在图1 中，功率传输回路与控制回路分别对应两个不同的旋转dq 参考坐标系。功率传输回路对应的dq 坐标系由输电线上实际的PCC 电压确定，称为系统dq 坐标系。而控制回路对应的dq 坐标系由PLL 输出的相位信息确定，称为控制器dq 坐标系。系统dq 坐标系与控制器dq 坐标系之间的相位关系如图2 所示。当PCC 电压出现扰动时，PLL 输出的相位信息与实际的PCC 电压相位之间会出现偏差，这会使得2 个dq 坐标系之间出现相角误差δ，而该误差只有在并网逆变器系统恢复稳态时才会消失。为反映2 个坐标系之间的差别，将电压、电流、占空比等电气量在系统dq 坐标系下的分量用上标s 表示，控制器dq 坐标系则用上标c 表示。

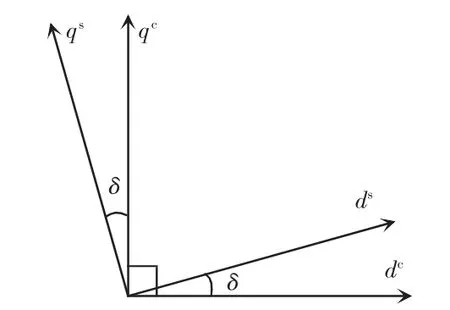
图2 系统dq 坐标系与控制器dq 坐标系Fig.2 dq coordinate frames for system and controller

若任意电气变量对应的矢量x 在控制器dq 坐标系下的d 轴与q 轴分量分别记为，而在系统dq 坐标系下的d 轴与q 轴分量分别记为与，则有

整理式（2）得到2 个dq 坐标系下小信号电量关系的表达式为

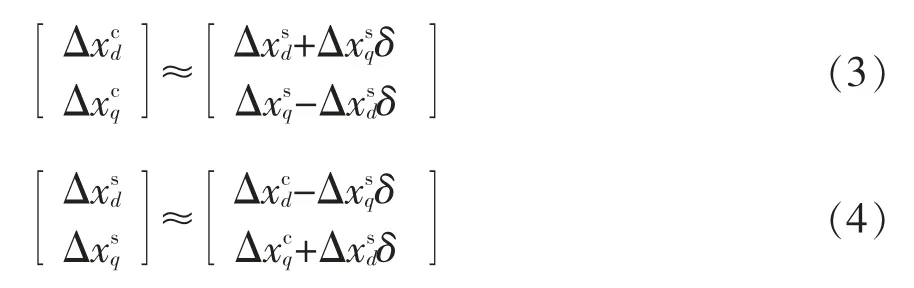
式（3）与式（4）中的相角误差δ 由PCC 电压的扰动与PLL 的动态特性共同产生。图3 为PLL 的控制框图，控制器dq 坐标系下的并网点电压q 轴分量输入PI 调节器TPLL（s），输出的角频率信号经积分后得到控制dq 坐标系相角θc，用于采样电量的dq 变换。

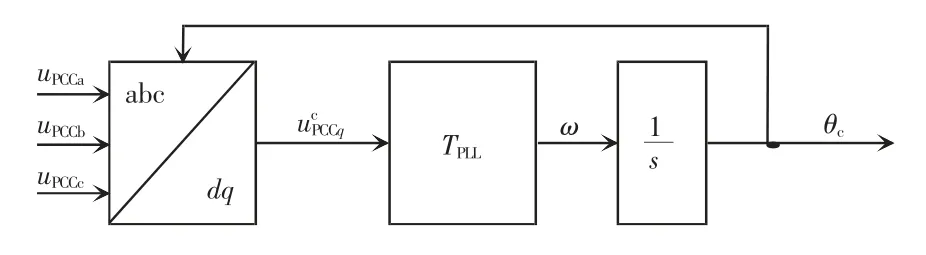
图3 PLL 控制框图Fig.3 Control block diagram of PLL

依次令式（3）、式（4）中的电量x 为电容电流iC、并网电流与占空比d，将式（6）代入式（3）、式（4）可得

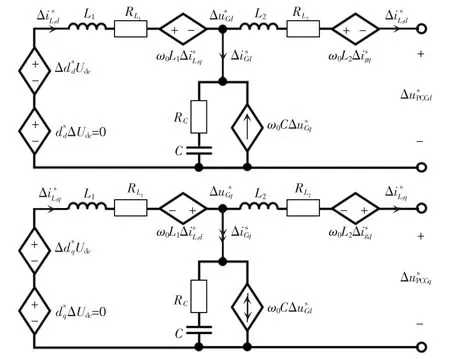
图4 系统dq 坐标系下的LCL 并网逆变器小信号电路模型Fig.4 Small-signal circuit model of LCL-type grid-connected inverter under the dq coordinate frame for system

由式（8）可知，当直流侧电压波动ΔUdc=0 时，在系统dq 坐标系下有

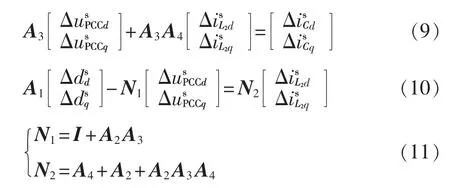
式中，I 为单位矩阵。

同时考虑锁相环与电流控制环，LCL 型并网逆变器的小信号模型如图5 所示。图中，Gi为电流控制环的PI 控制器，令kp、ki为其比例积分系数，有

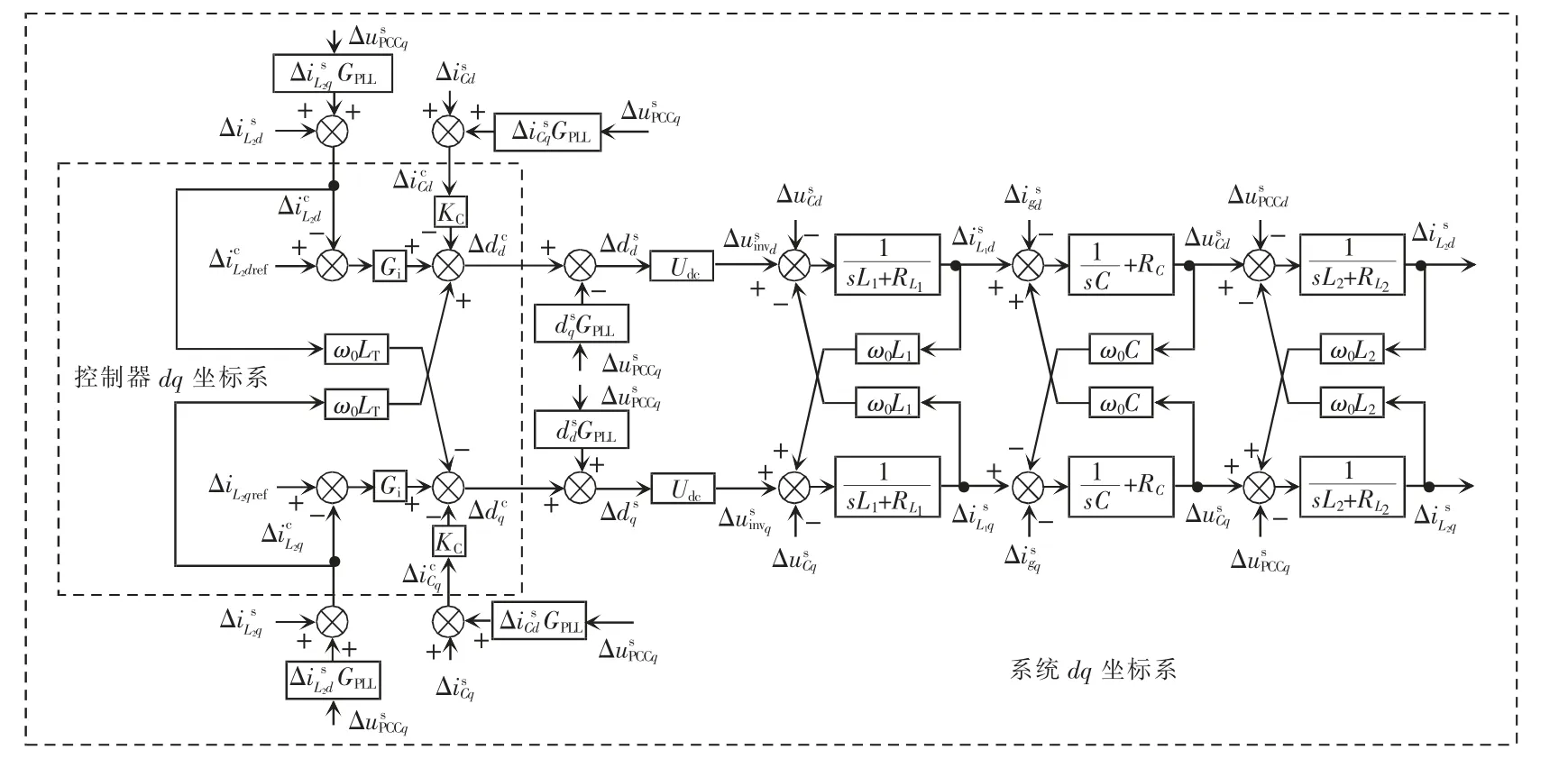
图5 LCL 并网逆变器的小信号模型Fig.5 Small-signal model of LCL-type grid-connected inverter

由图5 可知，当d 轴与q 轴参考电流保持不变，即ΔiL2dref=ΔiL2qref=0 时，在控制器dq 坐标系下有

矩阵Yinv即为LCL 型并网逆变器的小信号输出导纳矩阵。

2 系统稳定性分析

系统dq 坐标系下的电网输入阻抗矩阵可以写为

式中：Lg为电网等效电感；Rg为电网等效电阻。假设逆变器在理想电网条件下能正常工作，则当电网阻抗不可忽略时，当且仅当系统回比矩阵L（s）满足广义Nyquist 判据，系统稳定工作[17]。广义Nyquist稳定判据定义的回比矩阵L（s）表达式为

当L（s）的特征值的Nyquist 曲线在s 平面逆时针包围点（-1，0j）的净次数等于Yinv和Zg处在右半平面的极点总数时，级联系统稳定。由于电网在不含逆变器时稳定，逆变器单独工作时稳定，故Yinv和Zg均不含不稳定极点，则当L（s）的特征值的Nyquist 曲线不包围点（-1，0j）时，系统稳定。由于Yinv包含了逆变器控制回路的动态特性，故λ1与λ2的表达式形式复杂，应用广义Nyquist 稳定判据所需计算量较大，难以作为系统设计的指导。因此，本文利用盖尔圆定理来估计L（s）的特征值轨迹，从而实现对广义Nyquist 稳定判据的简化，降低其计算量。

3 基于盖尔圆定理的系统稳定性判据

盖尔圆定理提出了矩阵特征值在s 平面上分布范围的给定方法，由盖尔圆定理可以推得：回比矩阵L（s）的特征值必定处于如图6 所示的2 个盖尔圆内，即L（s）的4 个元素与L（s）的2 个特征值λ1和λ2之间的关系为

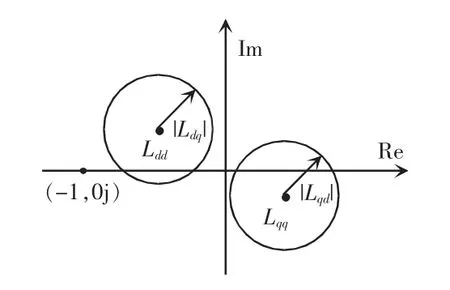
图6 盖尔圆定理Fig.6 Gershgorin theorem

单位圆允许域如图7 所示，若对于任何频率点，两个盖尔圆都被包含在s 平面上的单位圆内时，L（s）的特征值轨迹必定不包围点（-1，0j），则系统一定稳定。该稳定条件的充分条件为

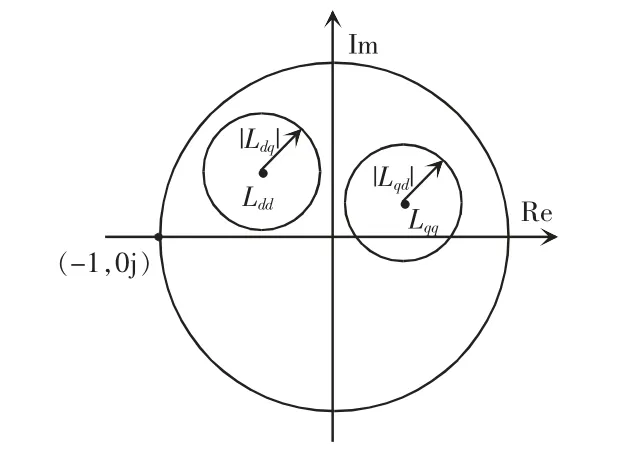
图7 单位圆允许域Fig.7 Allowed areas in unit circle

圆形允许域如图8 所示，为了给系统稳定留出一定的裕度，可以引入幅值裕度参数A（0＜A≤1），将单位圆缩小为以A 为半径的圆，该稳定条件的充分条件为

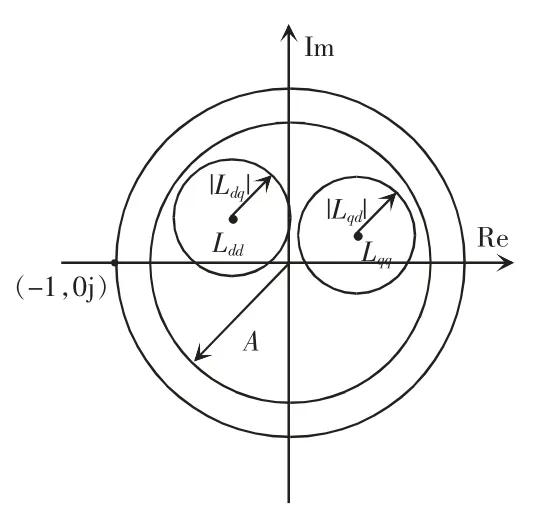
图8 圆形允许域Fig.8 Circular allowed area

该允许域表述简单，但保守性过强，对设计参数的限制过于苛刻。为了缩小盖尔圆在s 平面上的禁止区，如图9 所示，对于系统稳定裕度参数A（0＜A≤1），若对于任何频率点，两个盖尔圆都处于虚轴的平行线Re（x）=-A 的右侧，即2 个盖尔圆不进入图9 中的阴影区域时，L（s）的特征值轨迹必定不包围点（-1，0j），则系统一定稳定。该稳定条件的表达式为

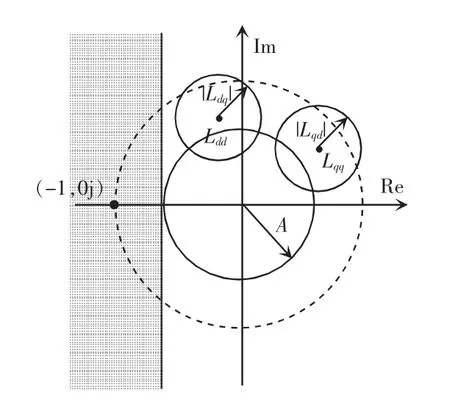
图9 禁止区1Fig.9 Prohibited area 1

为了进一步减小s 平面上禁止区的面积，减低稳定判据将稳定系统误判为不稳定的概率，可以同时引入系统稳定裕度参数A（0＜A≤1）与P（0＜P≤90°），构建如图10 阴影区域所示的禁止区。当2 个盖尔圆在任何频率点都不进入图10 所示的禁止区时，系统稳定。该稳定条件的表达式为

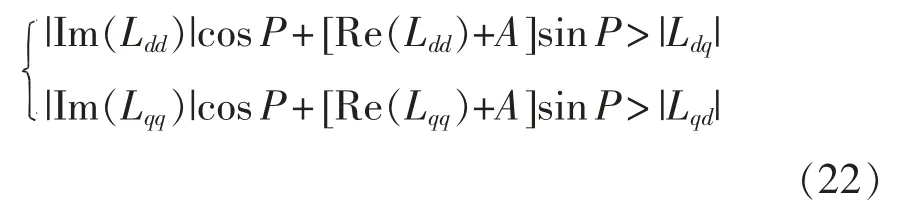
图10 禁止区2Fig.10 Prohibited area 2

4 仿真验证

为了验证本文提出稳定性判据的有效性，在Simulink 仿真环境中搭建了LCL 型并网逆变器与电网的交互系统，系统参数如表1 所示。

表1 系统参数Tab.1 System parameters

首先，利用前文的稳定判据来分析并网逆变器系统的稳定性。电网阻抗的增加会影响系统的稳定性，当并网逆变器交互系统中电网电阻Rg不变，电网电感Lg从0.02 mH 增加到0.15 mH 时，回比矩阵L（s）的特征值Nyquist 曲线变化趋势如图11 所示。由图11 可知，当电网电感增大到一定程度时，Nyquist 曲线开始包围点（-1，0j），这意味着交互系统将失去稳定，广义Nyquist 稳定判据得到的系统稳定临界点约为Lg=0.11 mH。

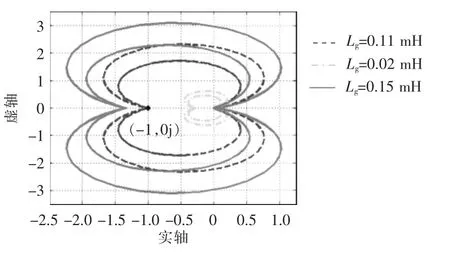
图11 广义Nyquist 稳定判据Fig.11 Generalized Nyquist stability criterion

应用如图8 所示的圆形允许域，设置系统稳定裕度参数A=1，定义

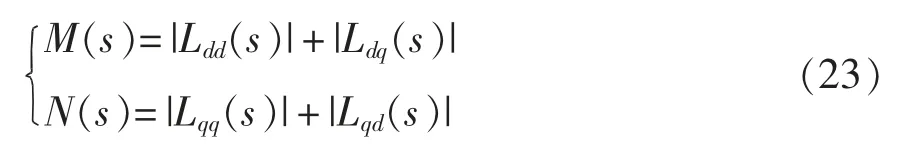
令电网电感Lg从0.02 mH 增加至0.05 mH，M（s）与N（s）的频率响应变化趋势分别如图12（a）与图12（b）所示。根据圆形允许域的定义，当M（s）与N（s）在任何频率点处都居于黑色虚线下方时，系统稳定。从图12 可以看出，该判据可以反映系统稳定裕度随电网电感增大而降低的趋势，其判断系统稳定的临界点约为Lg=0.033 mH，虽然该判据计算简便，且能够保证系统的稳定，但其结果与广义Nyquist 方法得到的结果相差较大，保守性过强。

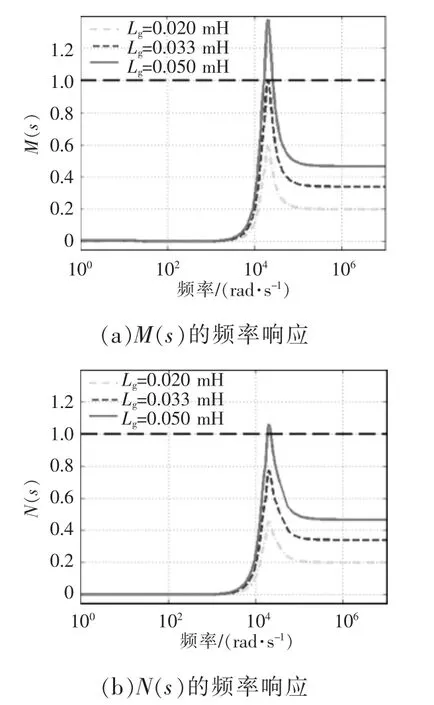
图12 利用圆形允许域判定系统稳定性Fig.12 Judging system stability by using circular allowed area

若应用如图9 所示的禁止区1，设置系统稳定裕度参数A=1，定义

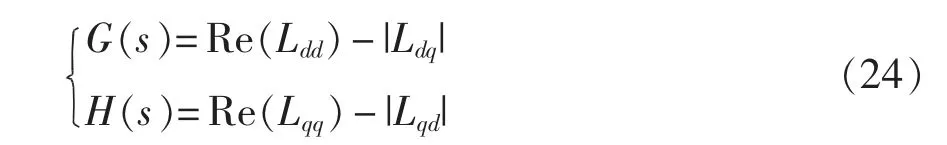
令电网电感Lg从0.02 mH 增加至0.08 mH，G（s）与H（s）的频率响应变化趋势分别如图13（a）与图13（b）所示。根据禁止区1 的定义，当G（s）与H（s）在任何频率点处都居于黑色虚线上方时，系统稳定。该判据判断系统稳定的临界点约为Lg=0.057 mH，从图13 可以看出，相比圆形允许域，禁止区1 的保守性有所降低。

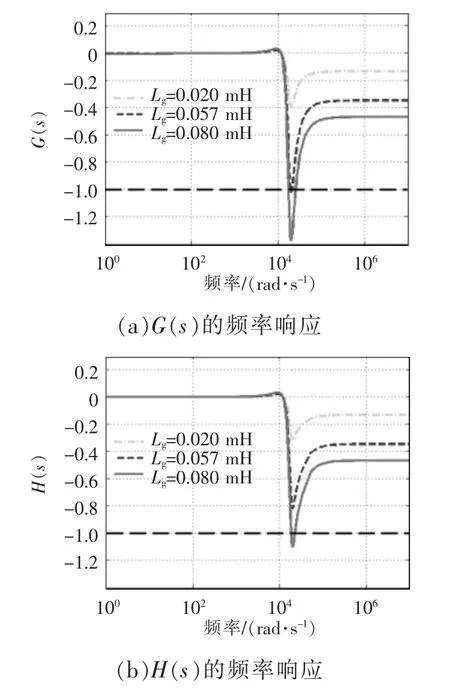
图13 利用禁止区1 判定系统稳定性Fig.13 Judging system stability by using prohibited area 1

若应用如图10 所示的禁止区2，设置系统稳定裕度参数A=1，P=10°，定义

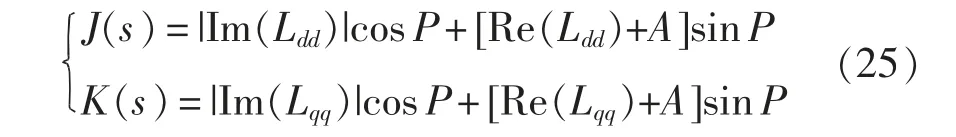
令电网电感Lg从0.020 mH 增加至0.120 mH，J（s）与|Ldq|的频率响应变化趋势如图14 所示，K（s）与|Lqd|的频率响应变化趋势如图15 所示。根据禁止区2 的定义，当J（s）在任何频率点处都居于|Ldq|上方，且K（s）在任何频率点处都居于|Lqd|上方时，系统稳定。该判据判断系统稳定的临界点约为Lg=0.085 mH，与应用广义Nyquist 方法得出的结果已经比较接近，由于该判据不需要计算L（s）的特征值，故该判据与传统的广义Nyquist 方法相比，计算量大大降低。

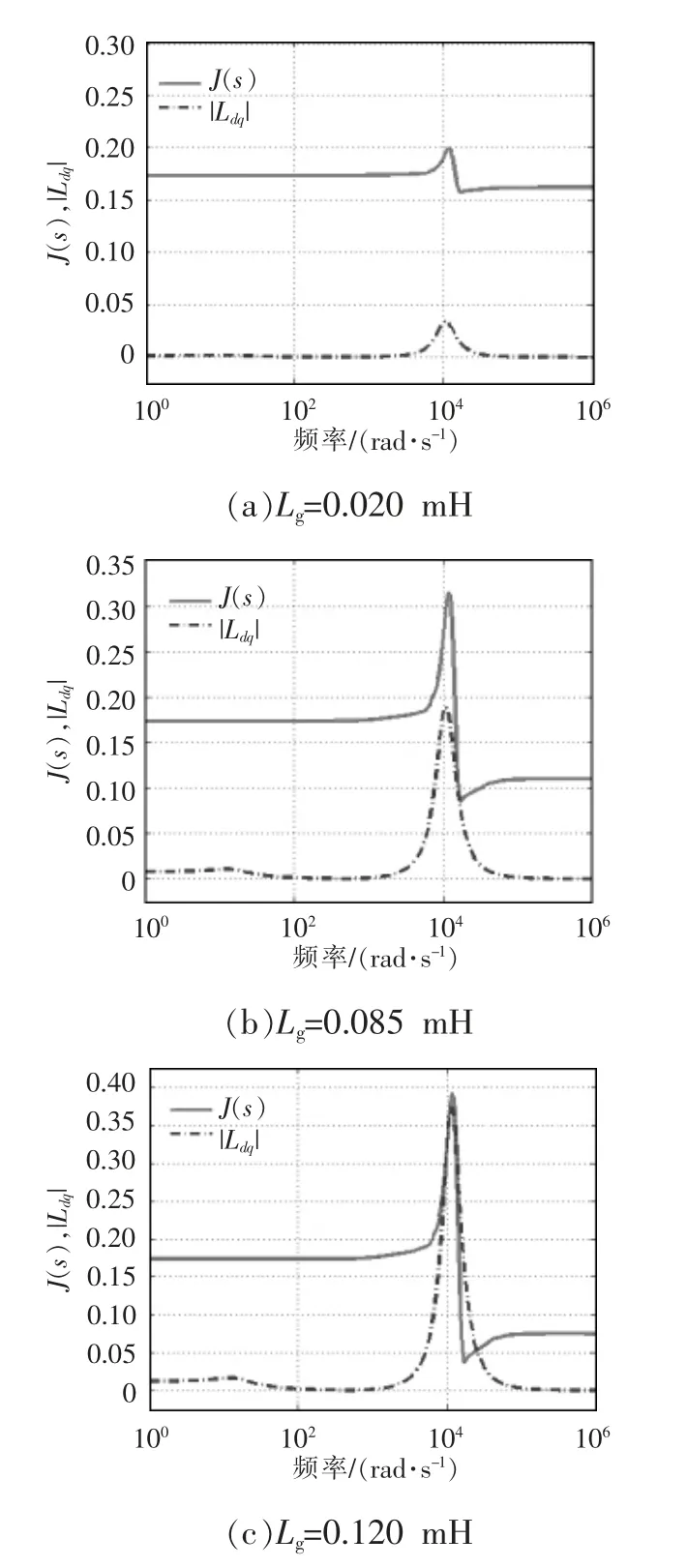
图14 J（s）与|Ldq|的频率响应Fig.14 Frequency response characteristics of J（s）and |Ldq|

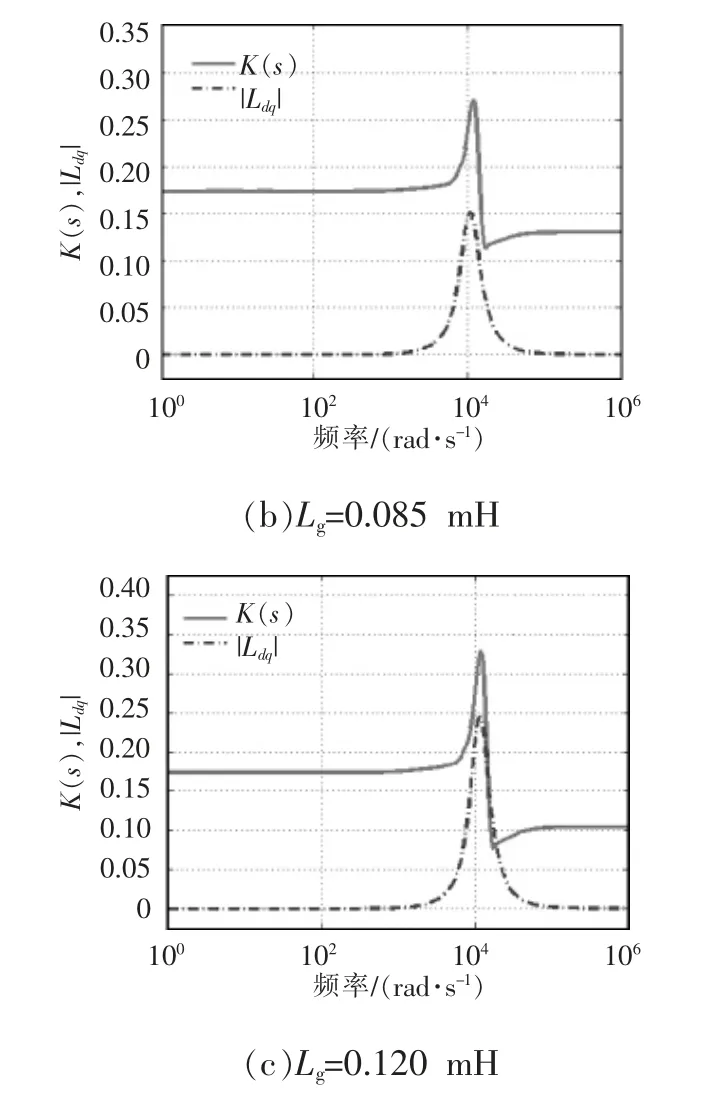
图15 K（s）与|Ldq|的频率响应Fig.15 Frequency response characteristics of K（s）and |Ldq|

利用Simulink 搭建的LCL 型并网逆变器系统仿真模型，对稳定性分析结果进行验证。在t=1 s 时，令电网电感Lg从0.030 mH 突升至0.085 mH，并网电压uPCC与并网电流波形如图16 所示。在t=1 s 时，令电网电感Lg从0.030 mH 突升至0.160 mH，并网电压uPCC与并网电流波形如图17 所示。

从图16 与图17 可以看出，当Lg=0.030 mH时，并网逆变器系统稳定，输出电压与电流波形所含的谐波较小，A 相PCC 电压THD=3.17%，Lg增大至0.085 mH 后，A 相PCC 电压THD=3.92%，系统仍能保持稳定，Lg增大至0.160 mH 后，并网逆变器系统出现了明显的振荡，进入不稳定状态，这符合禁止区2 所确定的判据给出的预测，说明该判据可以保证并网逆变器系统的稳定。由理论分析可知，该判据的保守性略高于传统的Nyquist 判据，但其优点在于计算量大幅下降，可以作为一种实用的系统稳定区域估算方法。

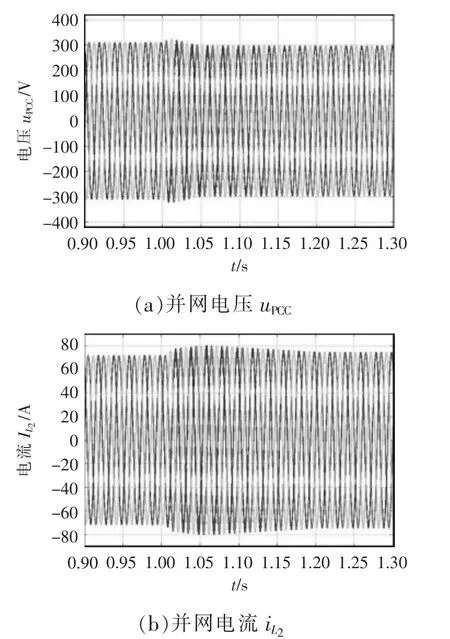
图16 Lg 从0.030 mH 突升至0.085 mH 时的逆变器输出仿真波形Fig.16 Inverter output simulation waveforms when Lg changes from 0.030 to 0.085 mH abruptly

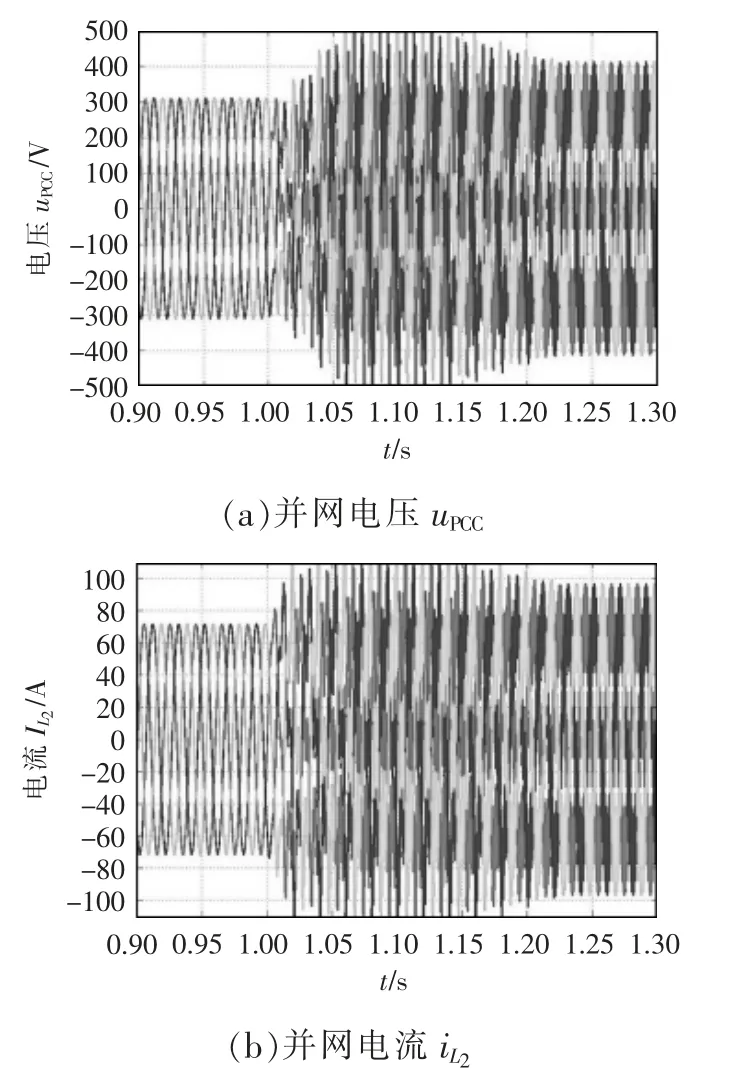
图17 Lg 从0.030 mH 突升至0.160 mH 时的逆变器输出仿真波形Fig.17 Inverter output simulation waveforms when Lg changes from 0.030 to 0.160 mH abruptly

5 实验验证

为验证稳定性判据的有效性，搭建了一个50 kW 的三相LCL 型逆变器实验平台，控制芯片采用TI 公司的32 位浮点型DSP，型号为TMS320F283 35，IGBT 采用RENESAS 公司的RJH60F5，系统参数如表1 所示。

设置电网电感Lg=0.030 mH，测得PCC 电压THD=4.12%，PCC 处的电压与电流波形如图18 所示。

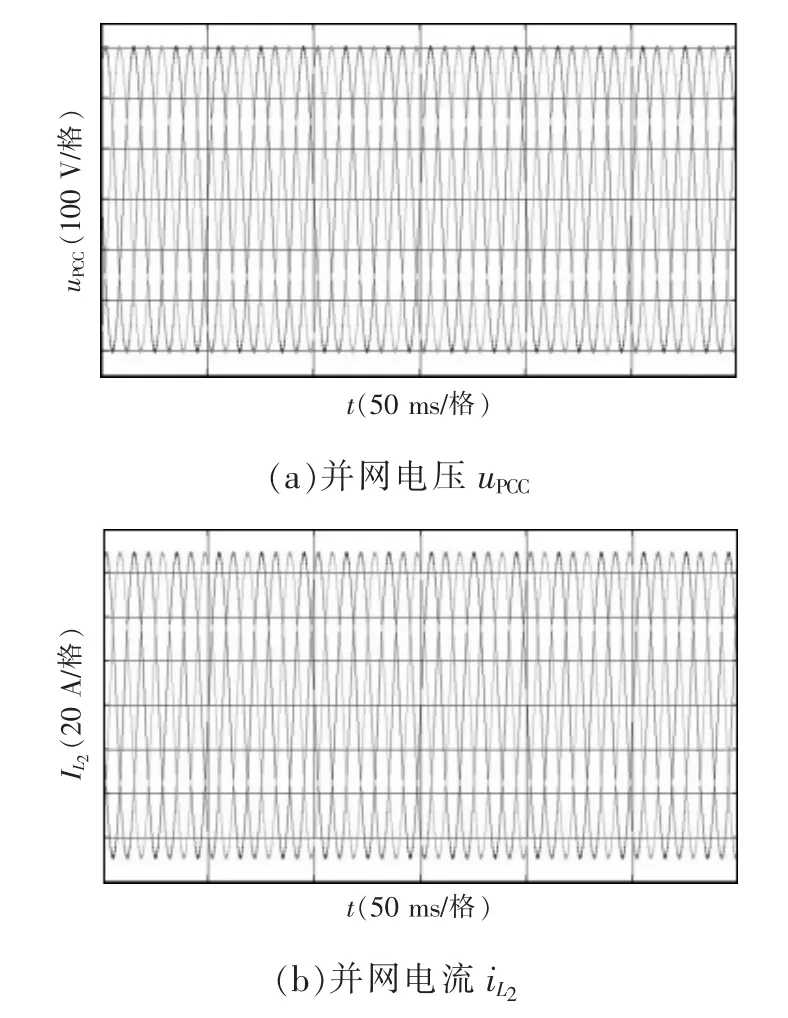
图18 Lg=0.030 mH 时的逆变器实验输出波形Fig.18 Experimental waveforms of inverter output when Lg=0.030 mH

将电网电感Lg增大至0.085 mH，测得PCC 电压THD=4.51%，逆变器输出波形中所含的谐波有所增加，PCC 处的电压与电流波形如图19 所示。

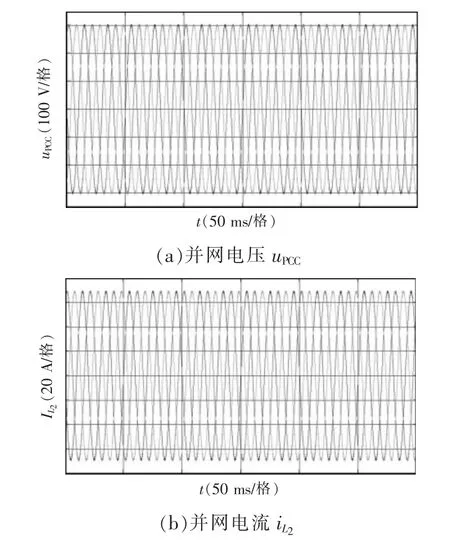
图19 Lg=0.085 mH 时的逆变器实验输出波形Fig.19 Experimental waveforms of inverter output when Lg=0.085 mH

将电网电感Lg增大至0.160 mH，观察到系统中出现了明显的振荡，PCC 处的电压与电流波形如图20 所示。

由图18～图20 可以看出，实验结果与仿真结果基本一致，随着电网电感Lg的增大，系统稳定性逐渐变差，禁止区2 所确定的判据可以保证并网逆变器系统的稳定，虽然该判据的保守性略高于传统的Nyquist 判据，但在实际应用环境下，在利用传统Nyquist 判据确定系统的稳定临界点后，不会直接应用稳定临界点来指导参数的设计，而是还需要在稳定临界点的基础上为系统留出一定的稳定裕度。也就是说，在能够保证系统稳定的前提下，对系统稳定临界点的判断在更加保守的方向上允许出现一定的误差，因此，本文提出的稳定判据在实际应用环境中可以充分发挥其计算量小的优势，作为一个实用的系统稳定临界点估算方法，在系统环境参数不断变化时，能够快速地估计出系统的稳定区域，且在保证系统稳定的同时，相比传统方法，保守性的上升也能保持在可接受的范围内。

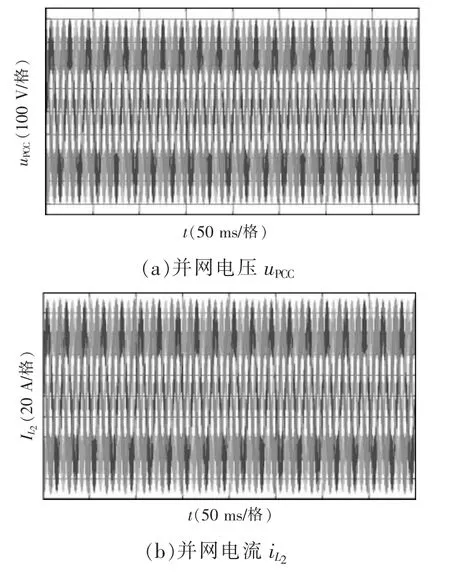
图20 Lg=0.160 mH 时的逆变器实验输出波形Fig.20 Experimental waveforms of inverter output when Lg=0.160 mH

6 结语

本文针对光伏并网逆变器系统进行了小信号分析，建立了dq 坐标系下的考虑锁相环与电流环补偿因素的并网逆变器系统小信号模型，提高了模型的精度。在此基础上，提出了一种基于广义Nyquist 理论的简化稳定性判据，通过盖尔圆理论来估计回率矩阵L（s）的特征值，通过在s 平面设置不同的禁止区来保证系统稳定。该判据与已有的广义Nyquist 稳定判据相比，以保守性的少许上升为代价，避免了直接计算L（s）的特征值，大幅度减少了计算量，在实际应用环境中，本文提出的稳定性判据可以充分发挥其计算量小的优势，作为一个实用的系统稳定临界点估算方法，在系统环境参数不断变化时快速估计系统的稳定区域，且通过引入系统稳定裕度参数，可以控制s 平面上禁止区的大小，为系统设计提供更高的灵活性。仿真与实验结果验证了稳定性判据的有效性。