考虑元件温-湿关联影响的氢燃料电池系统动态可靠性分析

高清振，时培成，潘道远

（1.安徽工程大学机械工程学院，芜湖 241000；2.安徽工程大学汽车新技术安徽省工程技术研究中心，芜湖 241000）

质子膜氢燃料电池在航空航天、新能源汽车等领域有广泛的应用，它具有复杂的结构和运行机理，尤其是元件之间存在较强的功能关联关系，这种关联影响使电池系统可靠性呈现复杂的多态动态变化特性。对于动态系统的可靠性分析，Castet J等[1-2]、曹颖赛等[3]、Lisnianski A 等[4]、Xing Liudong等[5]、Fan Hehong 等[6]、Shen Zupei 等[7]学者分别提出了Petri 网、Boolean 模型扩展法、Markov 法、Monte Carlo 仿真法、Bayesian 网络和GO 法等，并开展了相关研究，但上述方法均假设系统元件相互独立，没有考虑元件的关联关系。而Levitin G[8]、Zio E[9]的研究表明，元件的关联作用对系统可靠性具有较大影响。综上，研究元件关联作用对质子膜氢燃料电池系统可靠性的影响具有重要的现实意义，而此类研究目前鲜有报道。

本文将基于元件多态可靠性建模、关联元件转移矩阵、向量发生函数及Kolmogorov 方程等方法分析集流板、扩散层和催化层的状态分布与质子膜温度失效和湿度失效两方面的关联影响。

1 元件功能关联分析

如图1 所示，质子膜氢燃料电池[10]由集流板、扩散层、催化层和质子膜构成。双极板由具有槽通道结构的石墨或合金构成，用于气体分配、冷却液集流和电池密封；扩散层由碳布组成，起传播气体、水汽以及导电、散热的作用；催化层是由Pt/C 形成的薄层，用于加速电化学反应；质子膜用于传导质子并隔离电子及反应气体，一般由氟磺酸膜、nafion 膜、非氟聚合膜等构成，其功能受温度和湿度影响极大，当温、湿度不符合标准时，质子膜功能会失效。

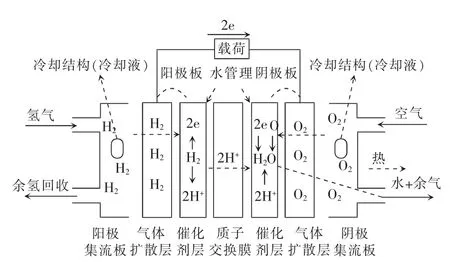
图1 质子膜氢燃料电池工作原理Fig.1 Working principle of proton membrane hydrogen fuel cell

氢燃料、空气和冷却液经集流板各自入口引入电池，氢燃料和空气用于电化学反应；冷却液保证质子膜工作温度稳定在100 ℃以内[11-12]；氢燃料和空气在引入时会被水汽增湿以保证质子膜湿度[13-14]。综上，对元件进行功能关联分析，如表1 所示。

由表1 可见，质子膜的可靠性状态除受自身性能衰减影响外，还依赖于集流板冷却结构的性能水平以及集流板、扩散层和催化层结构水汽通过率的性能水平。因此，元件关联作用集中在集流板、扩散层和催化层的可靠性状态对质子膜冷却和增湿效果的影响。

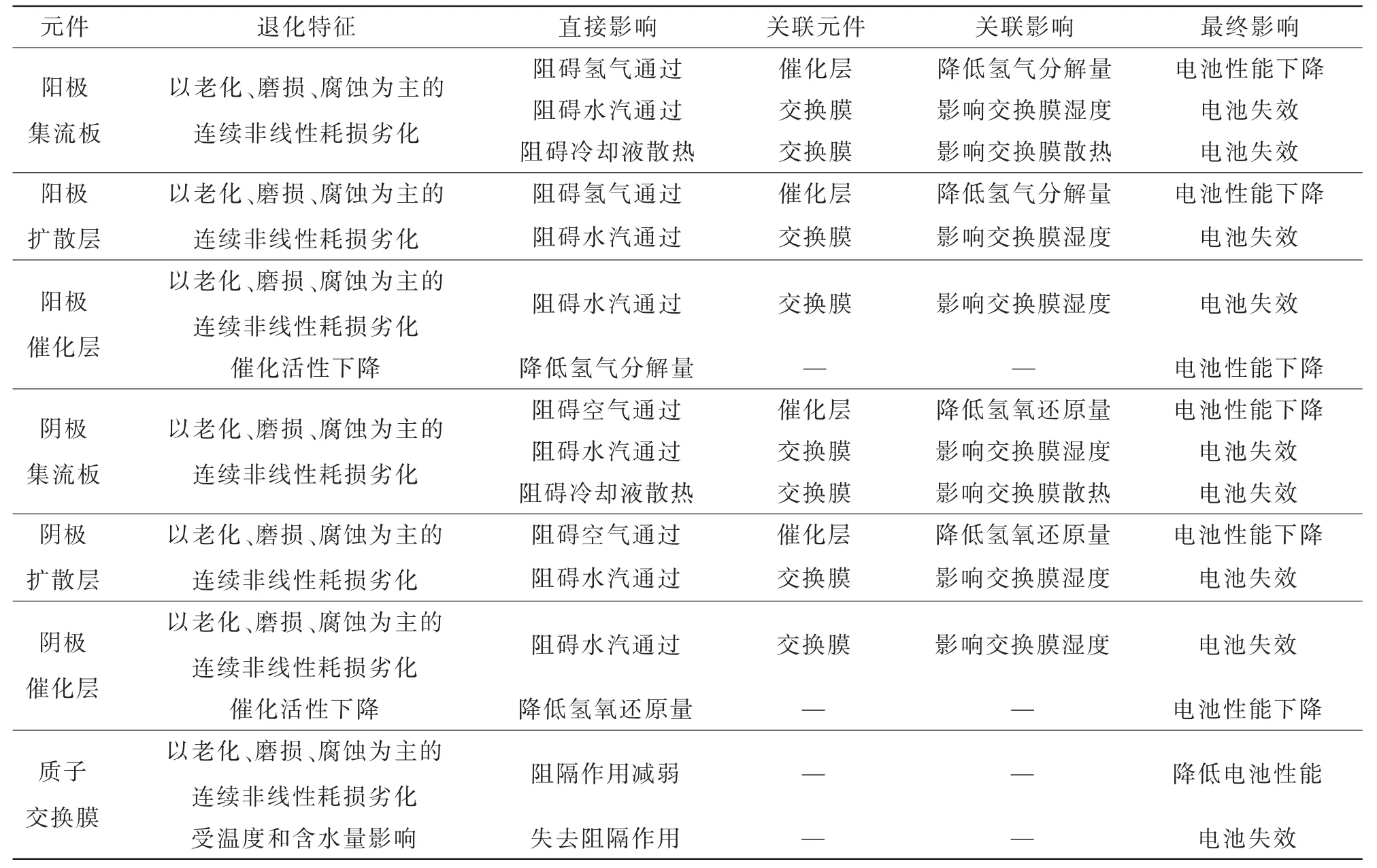
表1 元件功能关联关系Tab.1 Correlation relationship among element functions

2 元件退化过程建模

电池集流板、扩散层、催化层及质子膜在使用寿命周期里，由于老化、磨损、腐蚀等原因造成其性能连续非线性退化。首先将这种逐步退化状态采用Markov 方法[15]进行离散量化处理。假设元件k 的性能从正常状态退化到失效状态共经历N 个状态，该随机过程为连续时间内性能离散状态的合集，其中表征正常状态，表征失效状态。设为元件k 在t 时刻由m 状态向n 状态转移的概率，则以Markov 过程表征元件k 的性能状态转移率矩阵为

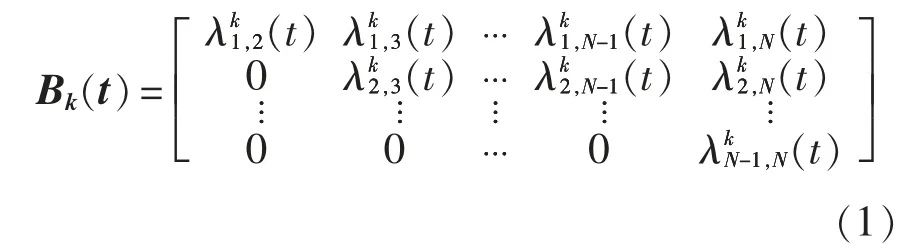
若元件k 初始状态确定，其不同状态时的稳态概率可以通过状态转移率矩阵和Chapman-Kol-mogorov 公式求得，元件k 的初始状态转移率矩阵可以通过对试验收据进行统计推算的方法求得。

3 元件关联特性分析

为便于分析，将对系统后续元件状态分布产生影响的元件定义为触发元件；将性能状态受系统上游元件状态分布影响的元件定义为关联元件；一个触发元件和其对应的关联元件构成一个关联组。对于氢燃料电池，触发元件为集流板、扩散层和催化层，关联元件为质子膜。元件k 各状态的性能值为的一个性能值子集对应关联元件l 的一种状态性能分布。Sk（t）由G 个互不相交的子集（l≤g≤G）组成，当k 的状态性能值属于某个子集时,元件l 的状态性能分布随之确定，关联元件l 的性能值表示关联元件l 在一个寿命周期里的状态总数。当，式中为k 的性能值属于子集时l 的性能值，Dl/g为l 此时的状态数，Dl/g≤Q。当元件的性能值逐渐劣化转移到另一个子区间时，关联元件的状态性能分布发生变化。

实际中，随着元件工作时间的增长及其内部损伤的积累，元件的状态转移概率在不同退化阶段是变化的且变化规律不一[16]。因此不能假定元件状态转移率是定值或是时间t 的函数，故引入状态转移系数η，且

式中:Mk为触发元件k 的性能子集总数；mk（t，n）为t 时刻触发元件性能状态值所处的性能状态子集数。设关联元件l 的初始状态转移矩为L1（0），则经过一段时间的性能退化之后,关联元件的状态转移矩阵为

4 关联系统多态可靠性计算

本处依据通用发生函数[17-18]表达具有关联特性元件的性能状态及其状态概率。已知元件k 的性能水平值为离散型随机变量，其通用发生函数可表示为

系统性能E 的分布用w 函数表示为

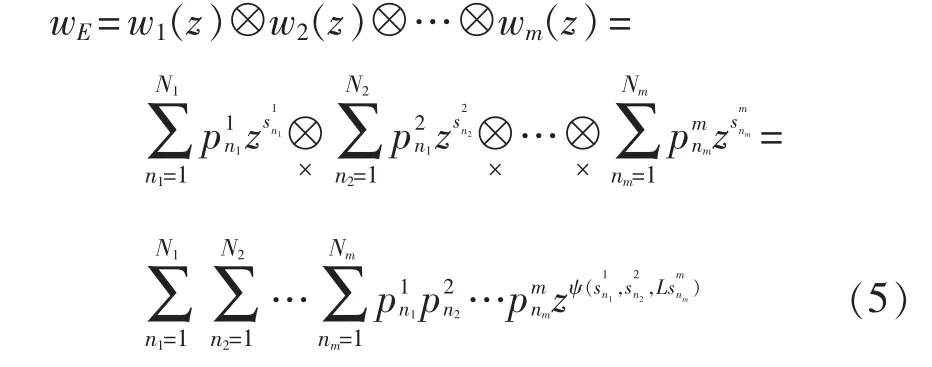
在一个由两个元件构成的关联组中，触发元件k 的性能子集共有G 个，根据前文分析可知关联元件l 在整个使用周期的状态概率矩阵Pl表示为

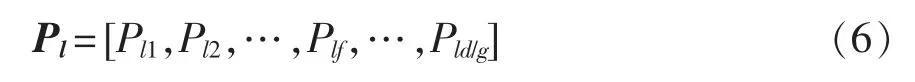
关联元件l 在第f 个状态所对应的状态概率可用向量表示为

l 的发生函数可表示为

由k 和l 组成的关联组的发生函数为

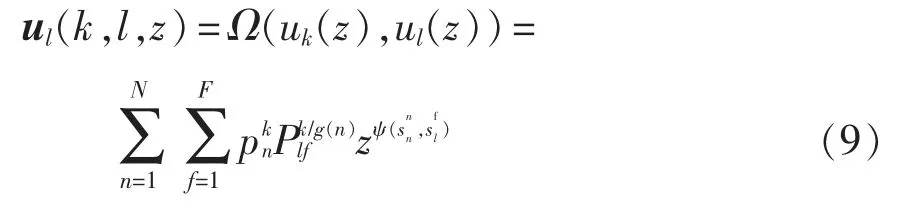
对于多元件组成的关联组则存在更复杂的关联关系，本处电池系统属于多个触发元件对应一个关联元件的情况，假设关联元件l 与触发元件a、b、c、…、k 分别关联，根据关联方式导出该关联组的发生函数为

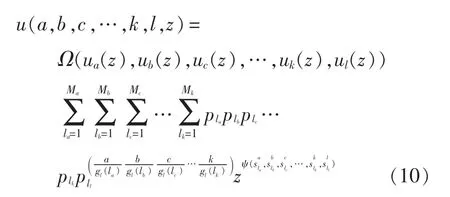
通过关联组发生函数和式（5），计算全系统的发生函数，根据系统设定的可靠性阈值可求得考虑元件关联特性时的系统可靠度[19]。

5 质子膜关联可靠性分析

5.1 单一关联组可靠性分析

简化集流板、扩散层、催化层与质子膜的关联关系如图2 所示。图中实线表示温度关联影响；虚线表示湿度和温度关联影响，其中湿度影响占绝对主导作用。温度影响是考虑循环加湿具有一些散热效果，虽所占比重较少，但为更贴合实际也将该关联因素考虑在内。且按可靠性功能划分，关联元件均为串联结构。

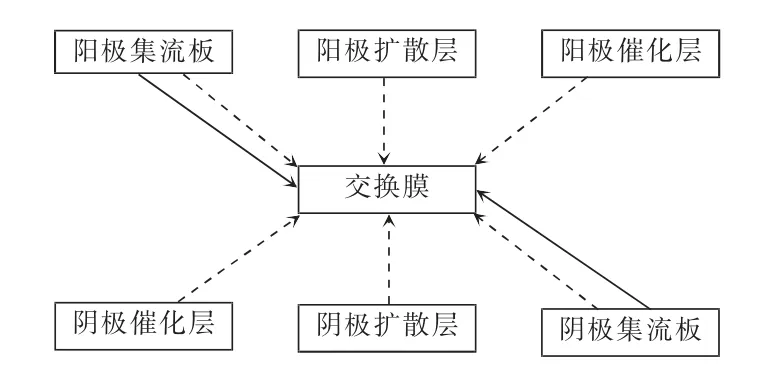
图2 元件关联关系Fig.2 Correlation relationship among elements

根据实际退化过程将元件划分为5 种状态，如表2 所示。

表2 元件状态类别划分Tab.2 Classification of state types of elements

通过试验检测流体通过率得到集流板、扩散层、催化剂层和交换膜的多状态性能水平值，设定退化过程不同状态为

集流板：S1（t）=S7（t）={5，4，3，2，1}；

扩散层：S2（t）=S6（t）={5，4.5，3.5，2.5.1.5}；

催化层：S3（t）=S5（t）={5，4，3，2，1}；

交换膜：S4（t）={5，4.5，4，3.5，3}。

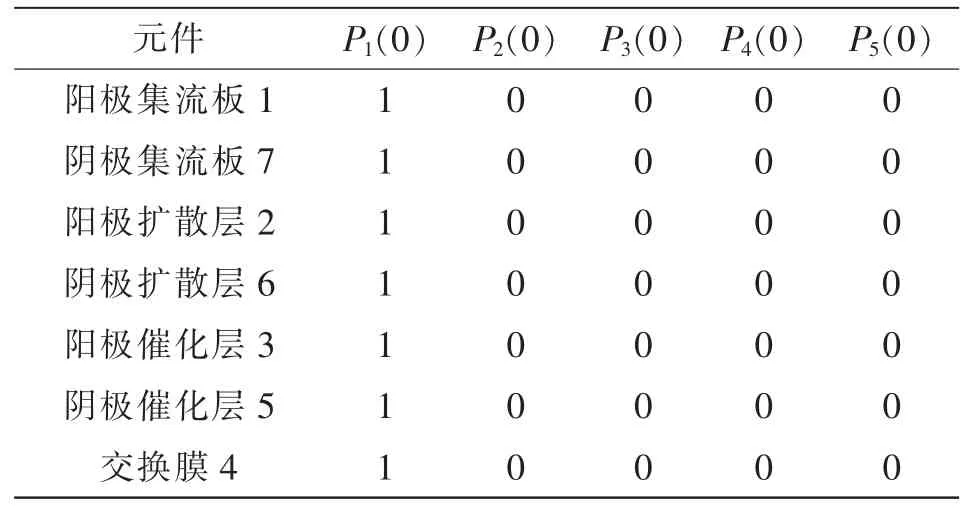
表3 元件初始状态概率Tab.3 Initial state probability of elements

通过Chapman-Kolmogorov 公式[20]导出关联元件4 的多状态概率微分方程为

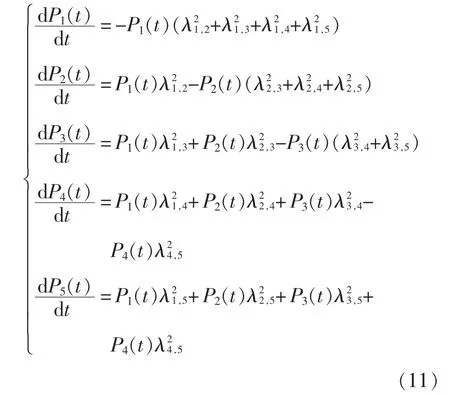
由图2 可知，交换膜与集流板、扩散层、催化剂层分别构成关联组。以阳极集流板与质子膜关联组为例分析温度关联特性，设集流板性能区间数M=2，根据式（2），当3.0≤≤5.0（m=2）时，交换膜的状态转移率系数η=1；当1.0≤＜3.0（m=1）时，交换膜的状态转移率系数η=2。交换膜在集流板处于不同性能区间时的状态转移率见表4，其状态概率见图3 和图4。

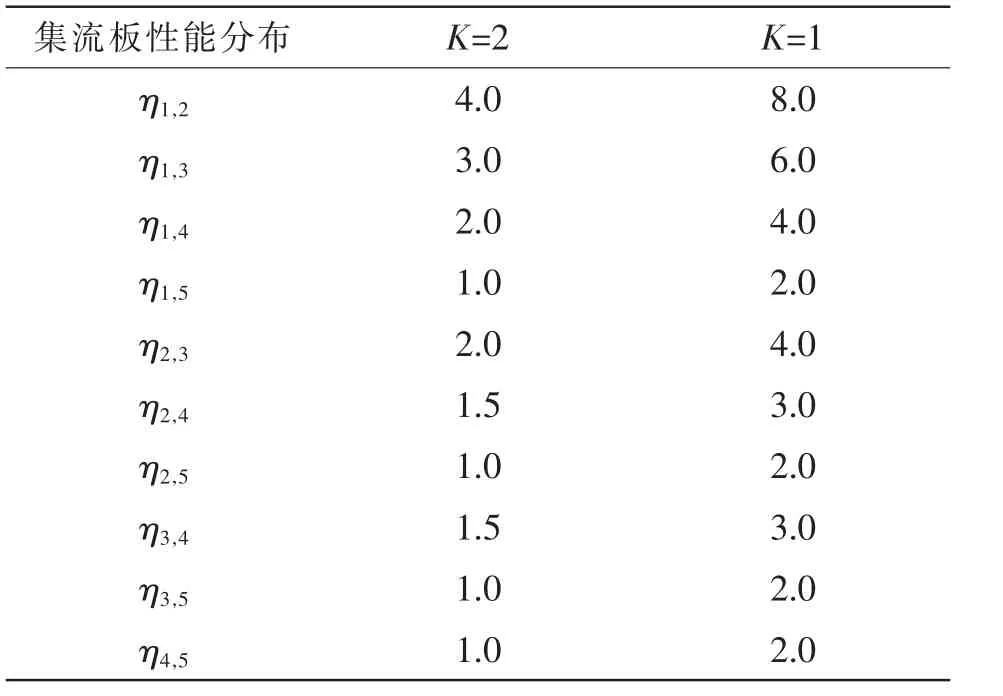
表4 质子膜状态转移率Tab.4 State transition rate of proton membrane 10-5/h

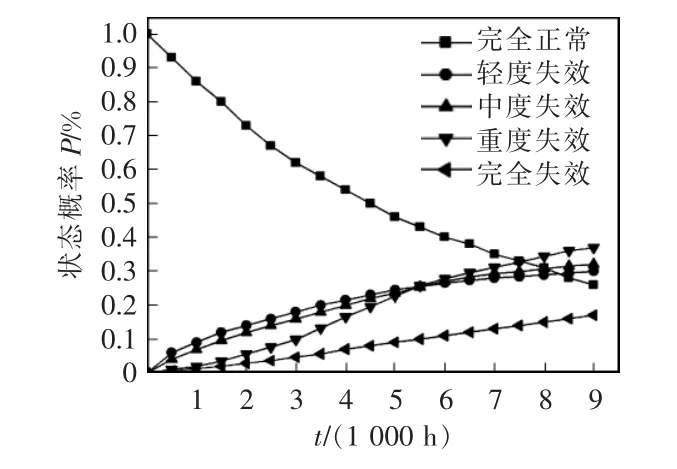
图3 质子膜温度关联状态概率（1.0≤＜3.0）Fig.3 Temperature-dependent state probability of proton membrane（1.0≤＜3.0）

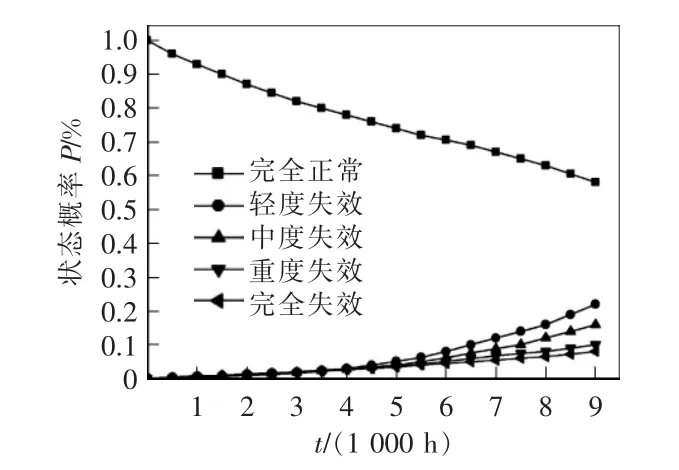
图4 质子膜温度关联状态概率（3.0≤≤5.0）Fig.4 Temperature-dependent state probability of proton membrane（3.0≤≤5.0）

通过图3 和图4 触发单元处于不同性能区间时的对比分析可知，触发单元性能状态偏高时，关联元件的各状态稳态概率曲线更平滑，即在相同时刻关联元件处于高性能的概率更大。在触发元件处于低性能状态时，关联元件的失效概率也会增大。

5.2 多关联组温度-湿度复合影响可靠性分析

为分析所有元件关联特性对系统可靠性的影响，取系统工作t=9 000 h 计算各元件的稳态概率。设各元件都是从最高性能的初始状态开始劣化，根据第2 节所述方法，计算7 个元件的多状态稳态概率，如表5 所示。

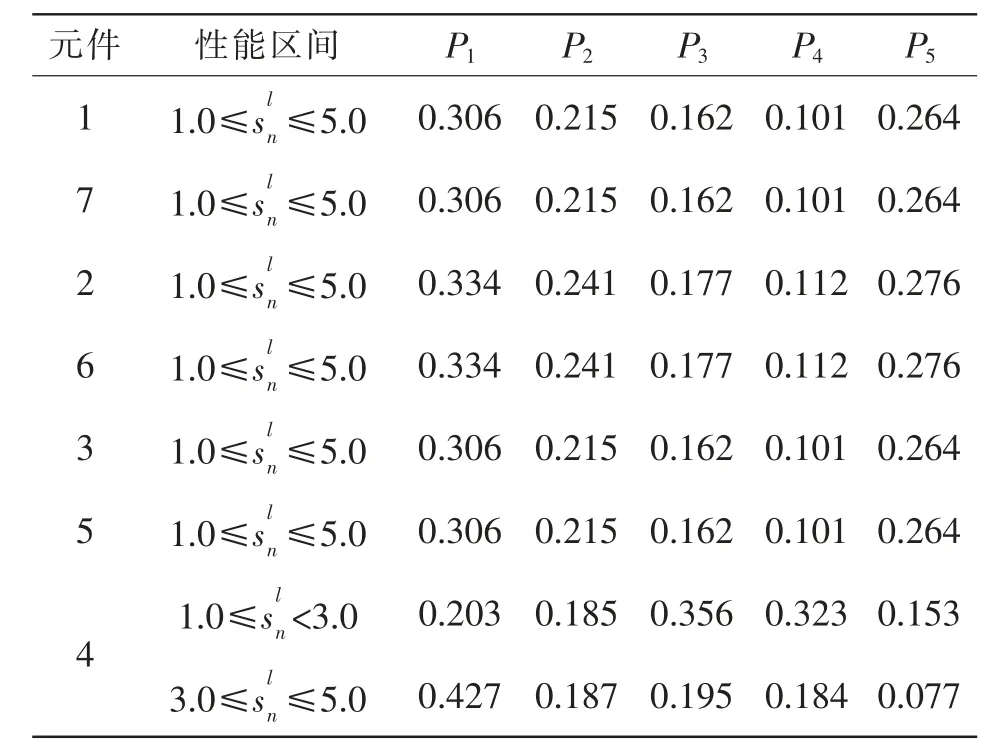
表5 各元件稳态概率Tab.5 Stead-state probability of each element

由表5 的稳态概率可知，在触发元件处于“完全正常”和“轻度失效”时，关联元件处于“完全正常”和“轻度失效”的概率会大些；反之，当触发元件处于“严重失效”和“完全失效”时，关联单元处于“严重失效”和“完全失效”的概率也会大些。元件的关联性通过稳态概率分布得到体现。

将触发元件和关联元件状态水平值通过改进的通用发生函数表示为

由式（5）～式（11）计算各关联组子系统性能状态发生函数，即

最终可求得考虑元件关联特性时的系统发生函数为

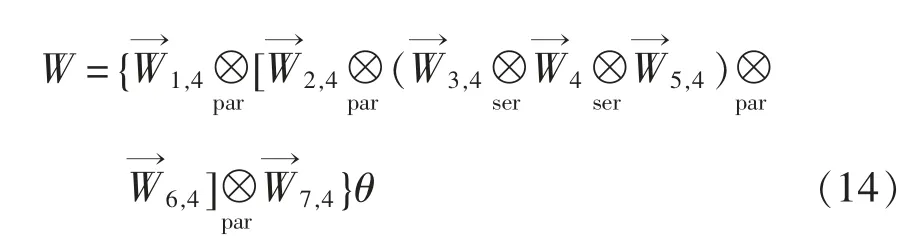
式中，θ 为湿度关联温度加权因子[21]，表征温度-湿度之间的复合关联影响，含义为增湿过程包含的散热效果，当湿度关联触发元件状态处于时，根据经验统计θ=1.05；当湿度关联触发元件状态处于时，取θ=1.1。

若不考虑元件关联影响，假设系统元件功能相互独立，在分析中将关联元件进行不相关处理，即设定关联元件的状态转移率矩阵在初始确定后不再改变，其他条件相同，导出系统发生函数为

从图5 可知，当系统的性能指标S 设定在3.0之前时，考虑了元件关联性的系统可靠度比相互独立时的可靠度要低，这是因为在设定工作时间内，随着系统的退化，组成系统的元件由于存在关联性，当处于低性能状态的触发元件发生失效后会增大其关联元件的状态转移率，即性能水平会同时降低到更低的状态;而独立元件失效并不影响其它单元，最终反映在系统上的结果即有关联性的系统可靠性降低更多。当性能指标S 设定在3.5 之后时，考虑了元件关联性的系统可靠度高于相互独立时的可靠度，这是因为触发元件的高性能状态决定了其关联元件的状态转移率较低，即一个关联组元件能同时保持在较高的性能状态。

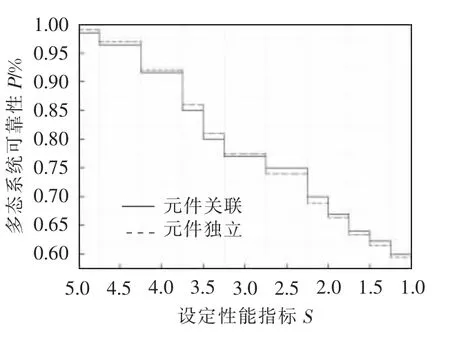
图5 两种情况下的多态系统可靠度Fig.5 Multi-state reliability of system in two cases

从图6 可见，质子膜可靠度随冷却关联元件性能的衰退而下降，尤其是随着工作时间的延长，当冷却关联元件性能处于低状态时，质子膜可靠度下降会更快；增湿元件状态的变化并不能改变质子膜可靠度随冷却关联元件性能衰退而下降的趋势，但当增湿元件状态处于高状态时，质子膜可靠度略有提高，说明增湿循环过程具有一定的冷却作用，但效果有限。

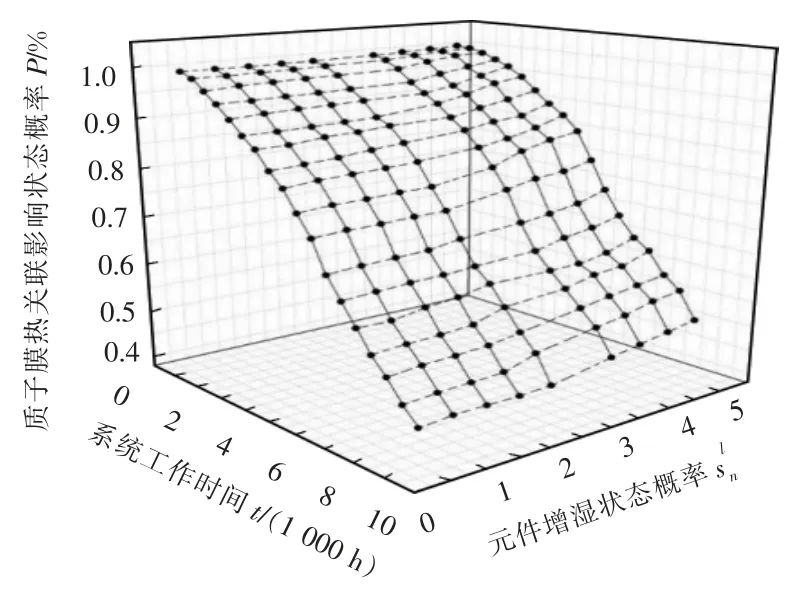
图6 质子膜温度-湿度复合影响下的可靠度概率分布Fig.6 Probability distribution of proton membrane reliability under the combined influence of temperature-humidity

6 结论

（1）利用元件功能关联分析方法，可以清楚地展示集流板、扩散层和催化层对质子膜工作温度和湿度的关联影响。因此，若按传统方法，只根据元件自身性能水平计算系统可靠度，而不考虑元件的关联作用，得到的结果不够准确。

（2）对于质子膜氢燃料电池等具有元件关联特性的多态动态复杂系统，通过Markov 模型描述元件的多状态退化过程、利用状态转移系数构建元件关联情况下的状态转移矩阵、依据发生函数建立系统可靠性分析模型的方法具有可行性。

（3）研究表明，在集流板、扩散层和催化层处于高性能状态时，质子膜的关联特性使系统的可靠性提高，而这些元件在低性能状态时，质子膜的关联特性使系统的可靠性降低；冷却关联元件的性能状态对系统可靠性的影响比湿度关联元件性能状态的影响大，因此提高集流板的性能状态有助于提升系统可靠性。