一种线性卡尔曼滤波的并网逆变器的自适应准PR 控制器

娄一川，梁理程，杨 浩，滕馥遥，宋国杰，陈延明

（广西大学电气工程学院，南宁 530004）

在偏远地区、海岛等电网末端的弱电网中，低短路容量的电气特性使电网的短路承载能力降低，负荷变化容易引起电网电压波动，高电网阻抗容易导致谐波共振和电网电压波形畸变。畸变的电网电压容易使光伏并网逆变器锁频环FLL（frequency locked loop）出现偏差甚至失效，并导致电能质量降低，因此弱电网下的电网同步方法至关重要。

目前采用的电网同步算法有离散傅里叶变换DFT（discrete Fourier transform）、最小二乘法等，但DFT 技术是建立在稳定波形的基础上，而用最小二乘法处理信号时，也需假定分析期间信号是静止的，这类方法不适合时变谐波估计。针对电网电压此类时变信号，很多学者提出采用FLL、锁相环PLL（phase locked loop）、卡尔曼滤波器等方法。在实际情况下，电网的相角多变，而频率比较稳定，即使发生漂移，其范围也比较小，因此学者研究了FLL 的同步算法。FLL 的主要优点是采用电网频率为反馈变量，进而估计输出电网电压的频率。文献[1]通过加入锁频环节，对频率偏移有较强的适应能力；文献[2]提出二阶广义积分器锁频环节SOGI-FLL（second order generalized integrator-frequency locked loop），能够准确估计电网电压基波和谐波分量；文献[3]对SOGI-FLL 进行了拓展，提出了多双二阶广义积分器，应用于三相不平衡的条件下。以上的FLL 技术虽然都可以达到预期的控制指标，但其对在含有大量环境噪声及测量噪声下提取基波信号不足。文献[4-7]提出了一种将卡尔曼滤波器和锁频环相结合的思路，利用FLL 使得卡尔曼滤波器自适应于电网频率的变化，但没有考虑三相的情况。

在文献[4，8]的基础上设计基于卡尔曼滤波器的三相锁频环结构，采用线性卡尔曼滤波器LKF（linear Kalman filter）准确估计电网电压的幅值、相角，讨论分析卡尔曼增益的大小决定在测量值与估计值两者之间信任程度问题及卡尔曼滤波器参数的选取。并通过将基于SOGI-FLL 准PR 控制器与加入线性卡尔曼滤波的锁频环LKF-FLL（linear Kalman filter-frequency locked loop）后的准PR 控制器的控制结果进行比较，来证明后者对电网频率追踪能力更优、动态性能更快、可以有效抑制噪音，对准PR 控制器的控制效果改善，电网电能质量得到优化。

1 基于频率自适应谐振控制策略的并网逆变器系统结构

SOGI-FLL 频率自适应准PR 控制策略，方法结构简单，稳态精度高，但动态跟踪误差大，动态性能有待提升，且不能有效抑制测量过程中的噪声和估计噪声。本文针对以上不足提出LKF-FLL 频率自适应准PR 控制策略，结构如图1 所示。

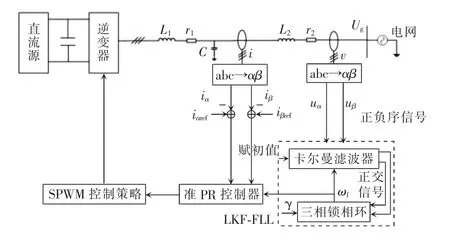
图1 基于LKF-FLL 的三相并网逆变器控制系统Fig.1 Control system of three-phase grid-connected inverter based on LKF-FLL

对于三相并网逆变器，在αβ 两相静止坐标系中，并网逆变器控制系统结构示意如图1 所示（为了绘制方便用单线表示三线拓扑）。L1、r1分别为逆变器侧电感及其寄生电阻；L2、r2分别为网侧电感及其寄生电阻；iα、iβ为αβ 两相静止坐标系中的输出电流；uα、uβ为αβ 两相静止坐标系中电网电压；γ 为频率跟踪环节的比例增益；ωf为电网电压估计值。

用卡尔曼滤波器估计电网状态，针对基频观测采用三相锁频环，通过误差分析提出频率自适应三相锁频结构，同时提升FLL 动态性能与抗干扰能力，通过线性卡尔曼滤波器与准PR 控制器的结合，保证准PR 控制器一直工作在谐振点，对并网逆变器的电能质量起到一定改善。

2 LKF-FLL 的结构与原理

卡尔曼滤波器算法具有收敛平稳、速度快、精度高、有效抑制噪声等优点。使用状态空间概念来描述系统，其状态量每一次的更新仅取决于前一次估计值和新的输入数据，不需要过去所有数据，节省空间，提升了运算速度，估计值也更加有效可靠。LKF-FLL 利用LKF 对电网电压采样，得到基频电压和基频电压的正交值，计算出电网频率，使LKF跟随频率变化调整控制器。LKF-FLL 的框图如图2所示。

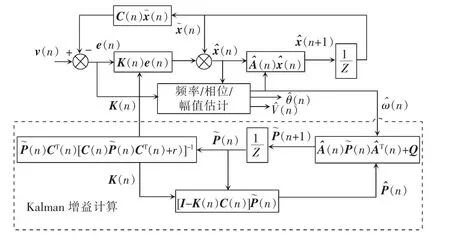
图2 LKF-FLL 的框图Fig.2 Block diagram of LKF-FLL

由图2 可知

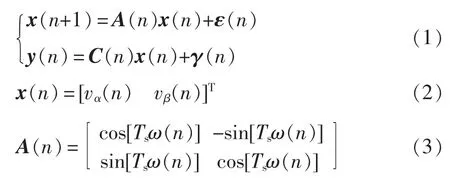
式中：n 表示当前值；x（n）为状态向量；A（n）为状态转换矩阵；y（n）为测量值；C（n）为测量矩阵，C（n）=[1，0]；Ts为采样周期；ω 为电网电压角频率；ε（n）为过称噪音矢量，ε（n）～N（0，Q），服从均值为0 和协方差为Q 的高斯分布，Q=qI（I 为单位矩阵）；γ（n）为测量噪音，γ（n）～N（0，r），不受ε（n）影响，服从均值为0，协方差为r 的高斯分布，本文中r 为标量。Q与r 的初值可以根据工程实际情况设定，通过LKF可以得到电网电压的基波跟一个与基波差90°的值。

预测公式为

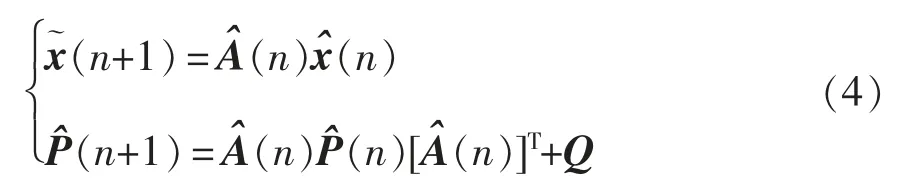
更新公式为

因离散域下分析LKF-FLL 控制算法较为困难，把离散域下的LKF-FLL 等效到连续域下，在式（1）第一式两边同时减去状态矢量x（n），再乘以1/Ts，经过运算可得

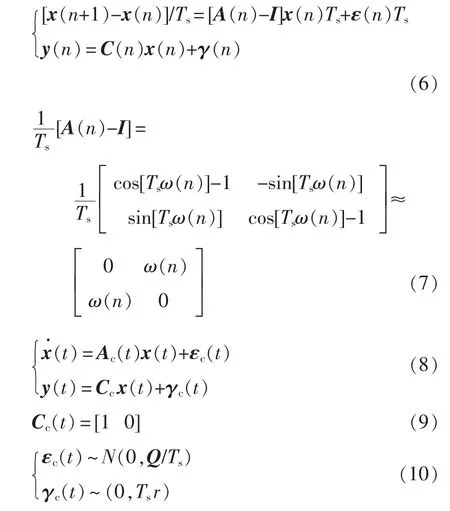
用式（4）、式（5）、式（6）和式（9）可以得到连续域下的误差协方差Pc（t），卡尔曼增益矢量Kc（t）和估算值的更新矩阵，表示为

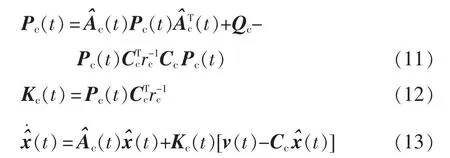
2.1 基波频率观测

电网电压频率随负载要求和发电不匹配波动，FLL 可自适应跟踪电网电压频率。FLL 原理如图3所示，图中，ωff为预设的角频率，ω'为电网的角频率估计值，误差e 为FLL 的输入变量。当电网频率锁定时，误差e 控制为0，v' 与v 相等。在系统中γ 系数的大小决定了FLL 的抗干扰能力和动态性能，当γ 值较大时，就会牺牲抗干扰能力来增加动态性能，当γ 值较小时则动态性能降低，在实际工程中根据实际需要选择γ 值。

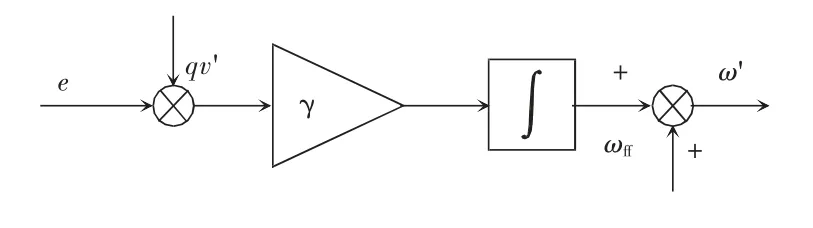
图3 FLL 原理Fig.3 Schematic of FLL

在图2 和图3 的基础上，本文设计的基于线性卡尔曼滤波器的三相锁频环结构原理如图4 所示。

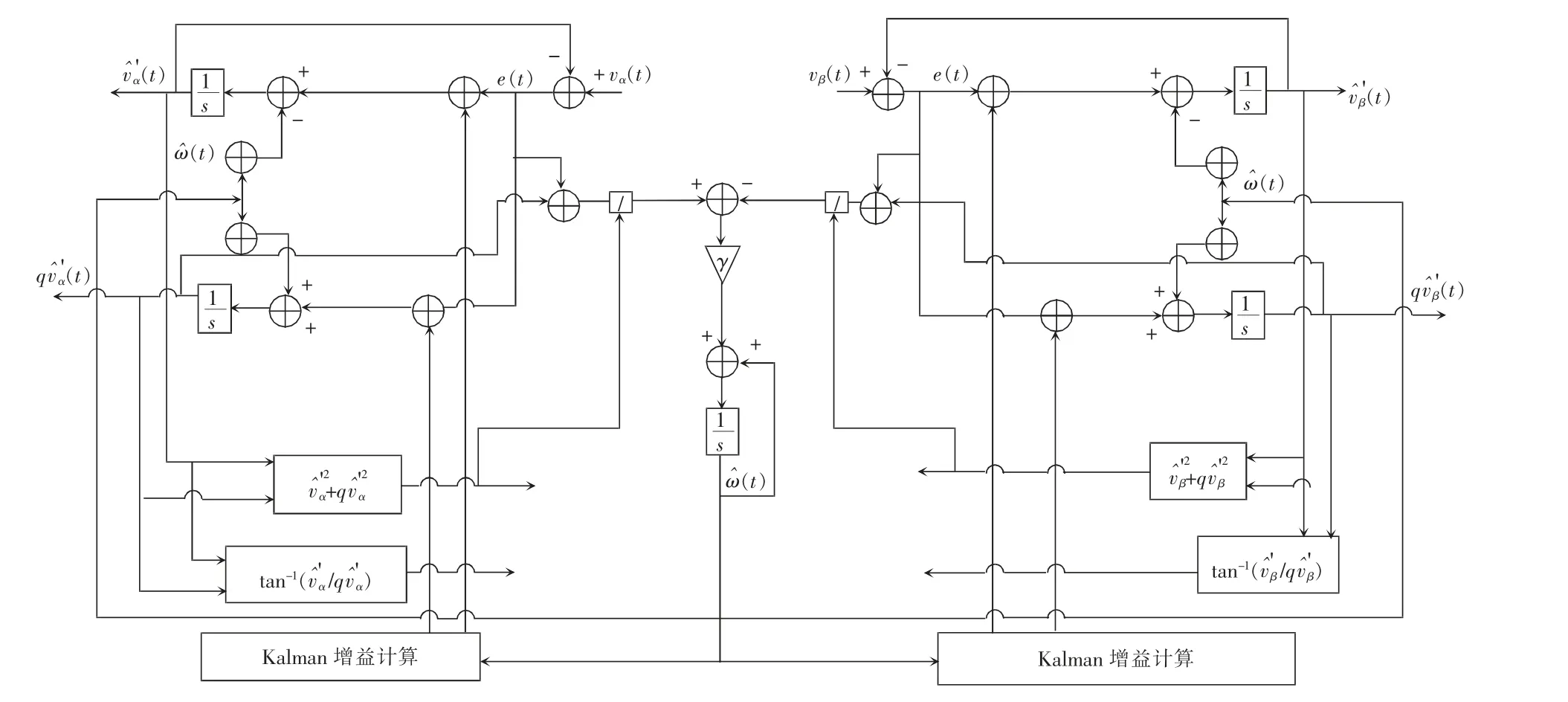
图4 三相锁频环原理Fig.4 Schematic of three-phase FLL

图中，vα（t）、vβ（t）为三相电网电压经3/2 变换后的输出值，为卡尔曼滤波器估计值，为对应信号的正交值。

2.2 滤波器的参数选取

预测方程式（4）表明预测的不确定性来自过程噪声和估计值的不确定性影响，初始值给定，通过更新方程式（5）来计算估计值与误差协方差，调整卡尔曼增益使更新后的误差协方差最小。在方程式（5）中，卡尔曼增益的大小取决于是偏向相信估计值还是测量值。若测量噪音足够小，那么测量值就比较可信，将卡尔曼增益调大；若预估值更可信，将卡尔曼增益调小。

定义误差协方差矩阵Pc（t）为

假设时间足够长，在系统到达稳定时令Pc（t）=0，此时可以得到卡尔曼增益系数kα和kβ的最优关系。

因为Pc（t）为对称矩阵，所以p2=p3，通过解方 程Pc（t）=0 可以得到

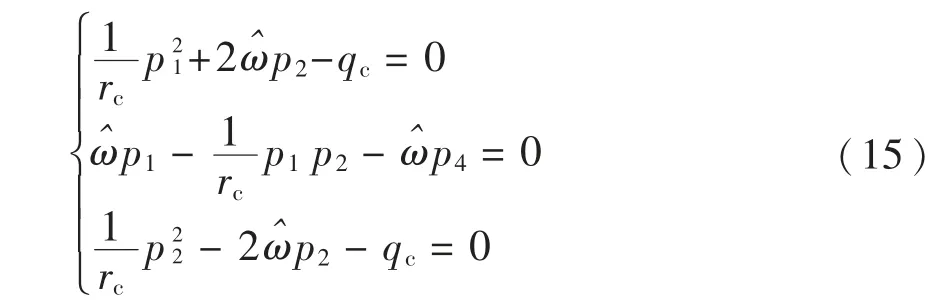
定义卡尔曼增益为

综合式（15）和式（16）得到

3 系统仿真及实验分析

3.1 仿真

本文搭建了Matlab/Simulink 仿真模型，对比LKF-FLL 和SOGI-FLL 的性能。采样频率为10 kHz，基波频率为50 Hz，通过负载切换、改变电网频率和给系统注入噪声进行仿真对比。仿真相关主要参数见表1。

表1 仿真实验相关主要参数Tab.1 Main parameters related to simulation

基于SOGI-FLL 策略和LKF-FLL 策略的准PR控制器仿真结果如图5 和图6 所示。

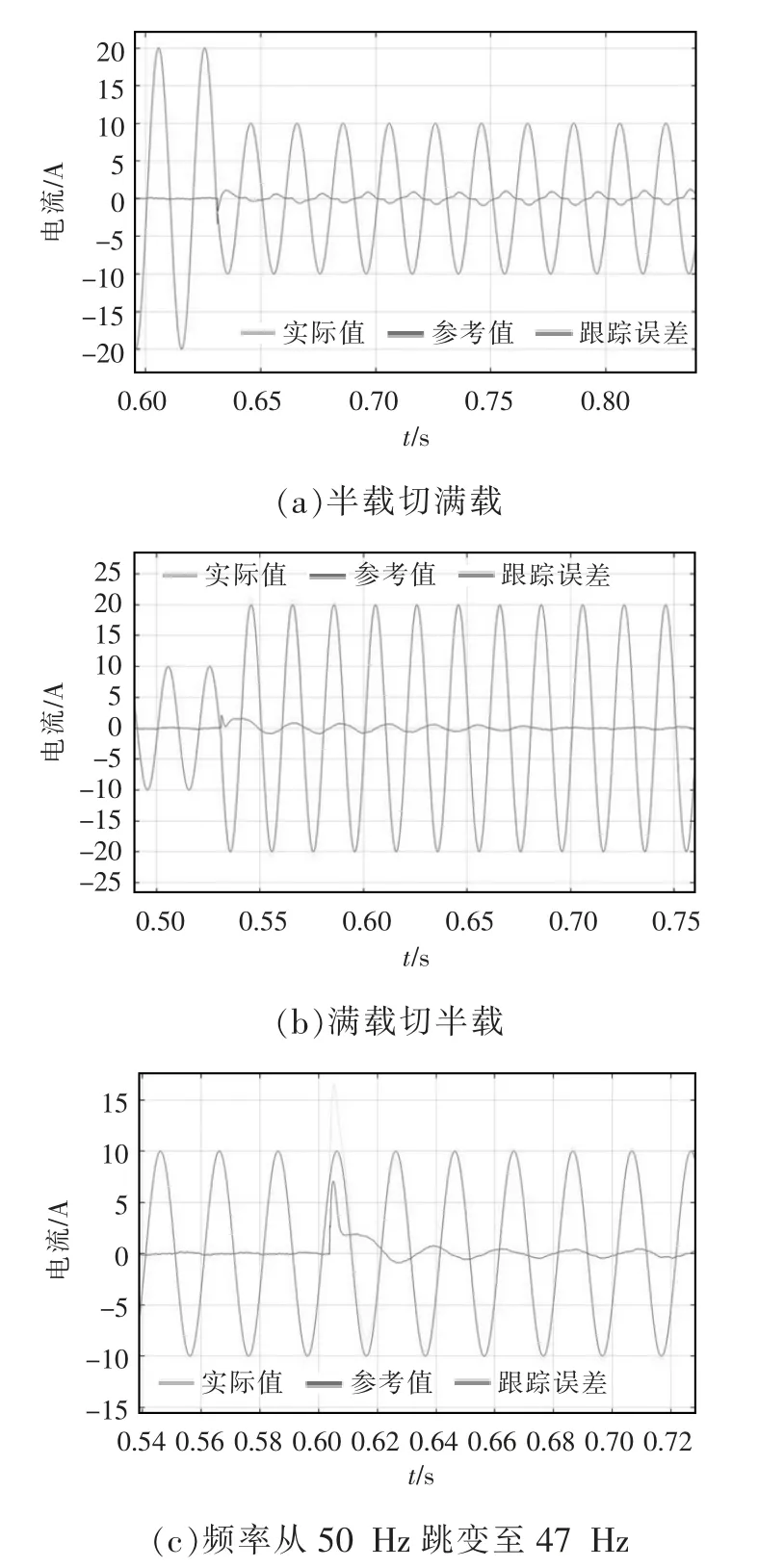
图5 基于SOGI-FLL 策略的准PR 控制器仿真结果Fig.5 Simulation results of quasi-PR controller based on SOGI-FLL strategy

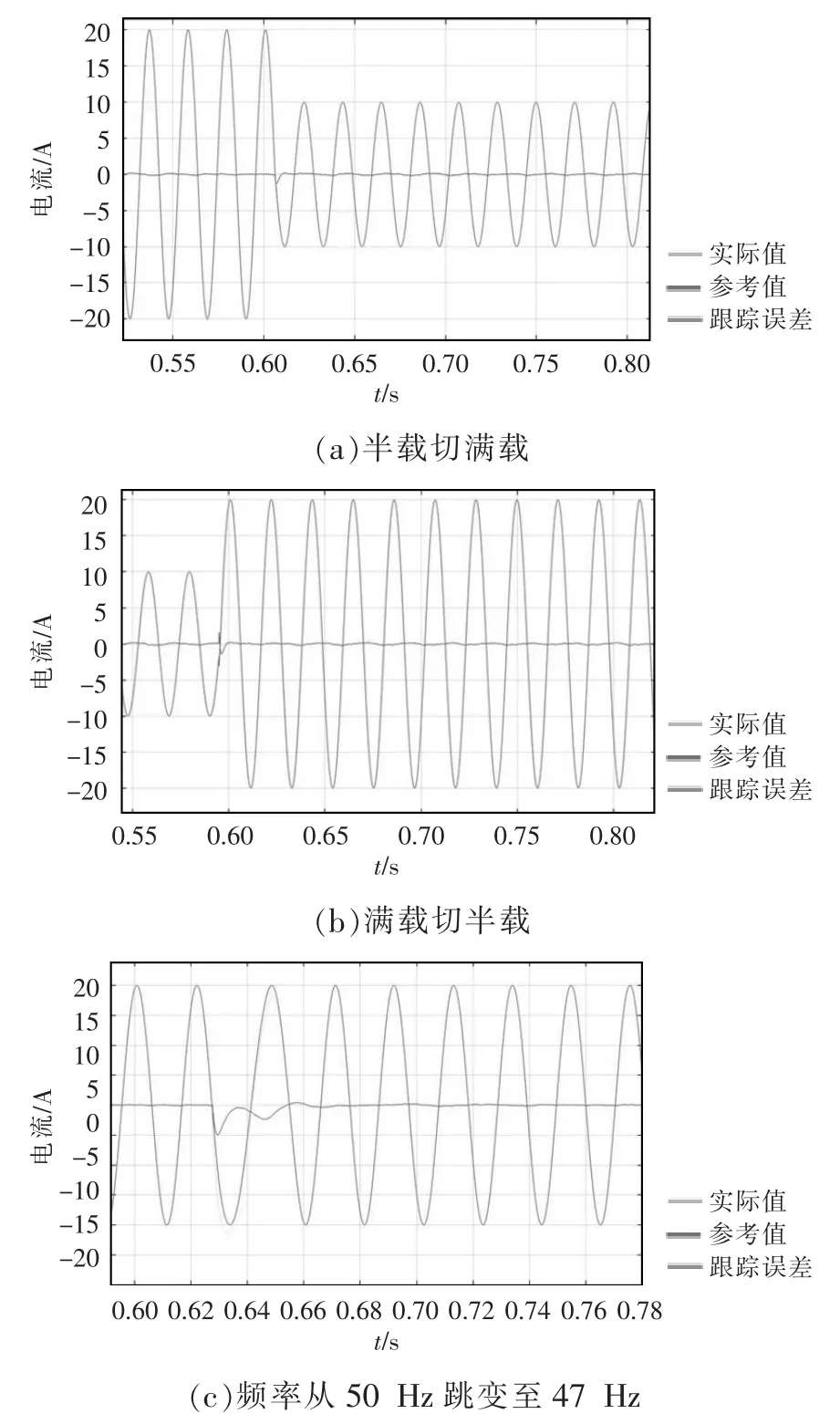
图6 基于LKF-FLL 策略的准PR 控制器仿真Fig.6 Simulation of quasi-PR controller based on LKF-FLL strategy

由图5、图6 可见电网频率从50 Hz 跳到47 Hz后，改变参考电流，基于SOGI-FLL 的准PR 控制器的控制精度下降，其电流跟踪误差出现波动，而基于LKF-FLL 策略的准PR 控制器在电网频率发生偏移时具有较高的控制精度和较强的的频率自适应能力。

图7 为注入噪音后的仿真对比。图7（a）、（b）为注入的噪音；图7（c）中的频率幅度最大值为300 Hz，最小值为285 Hz，振幅较大，受噪音干扰影响较严重；图7（d）频率幅度最大值为298 Hz，最小值为293 Hz，振幅较小受噪音影响较轻，有抑制噪音的能力，且兼顾动态性能。

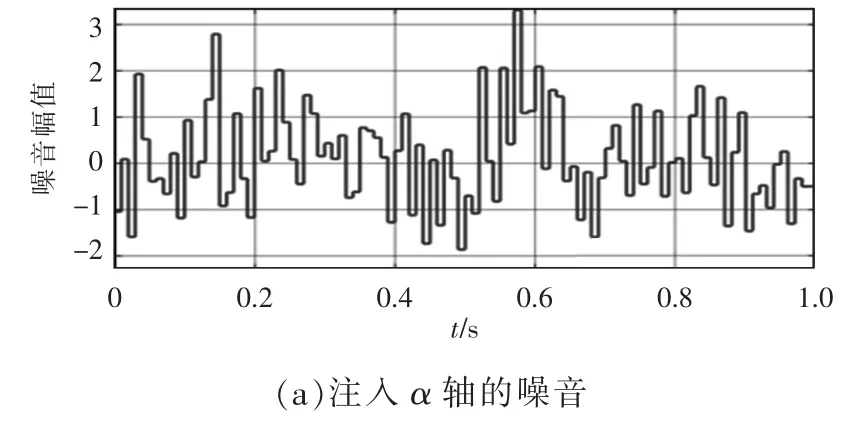
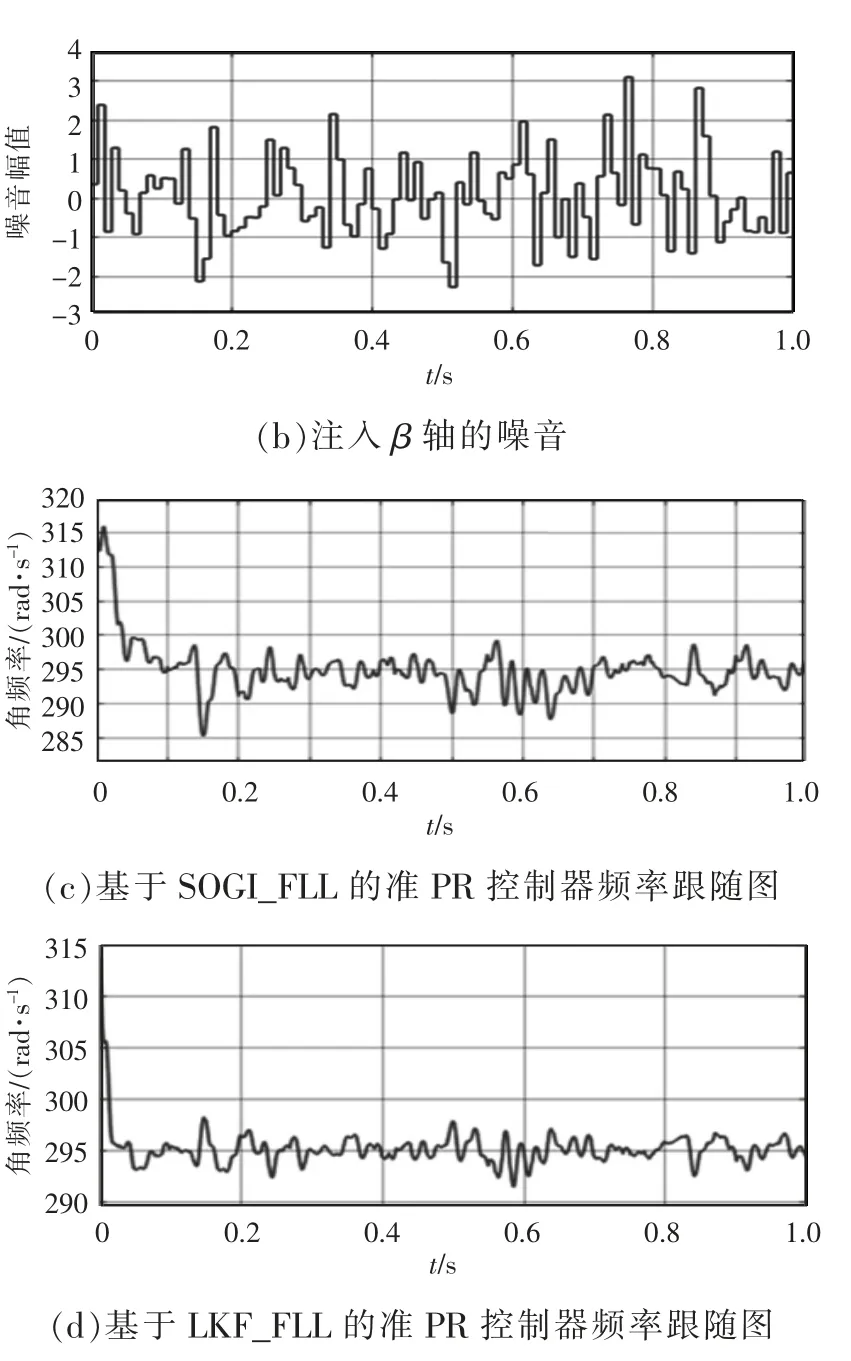
图7 测试抑制噪音的仿真对比Fig.7 Comparison of simulation of noise suppression test

3.2 实验结果

根据仿真模型，采用TI 公司TMS320F28335作为控制芯片，研制了额定功率为1.7 kW 样机实验平台，采样频率为10 kHz，交流侧100 V 电网电压通过电网接至变压器再接到调压器获得，直流侧电压180 V 通过直流稳压电源代替新能源发电提供，平台如图8 所示。

图8 实验装置及说明Fig.8 Experimental setup and its description

基于SOGI-FLL 策略和LKF-FLL 策略的实验结果对比如图9、图10 所示。图9（a）、10（a）为半载切满载（10 A 切换至20 A）A 相电流波形，基于LKFFLL 策略准PR 控制器的并网电流切换平稳，具有良好的动态性能，基于SOGI-FLL 策略准PR 控制器切换后，并网电流有少许畸变，经历近2 个周期恢复。将电网频率设为47 Hz，基于SOGI-FLL 策略的准PR 控制器输出电流出现波动，实际值跟踪参考值的拟合度相对较低，稳定后误差在±0.6 A 之间波动。基于LKF-FLL 策略的准PR 控制器输出电流的波动较小，实际值跟踪参考值得拟合度高，误差稳定在±0.2 A 之间波动。

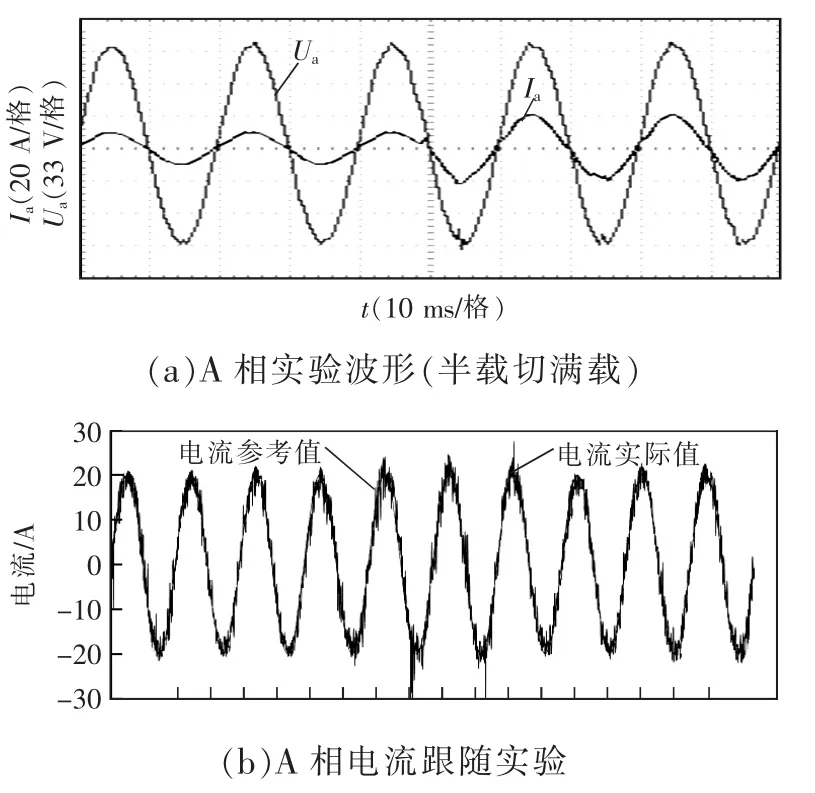
图9 基于SOGI-FLL 策略的准PR 控制器实验结果Fig.9 Experimental results of quasi-PR controller based on SOGI-FLL strategy

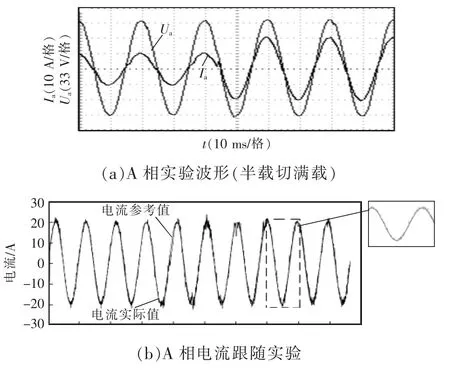
图10 基于LKF-FLL 策略的准PR 控制器实验结果Fig.10 Experimental results of quasi-PR controller based on LKF-FLL strategy

为验证引入LKF-FLL 后并网电流THD 值的有效性，进行了相应的对比实验，实验结果如图11、图12 所示，并网电流的THD 值由3.6%降为2.2%，并网电流的电能质量得到提升。

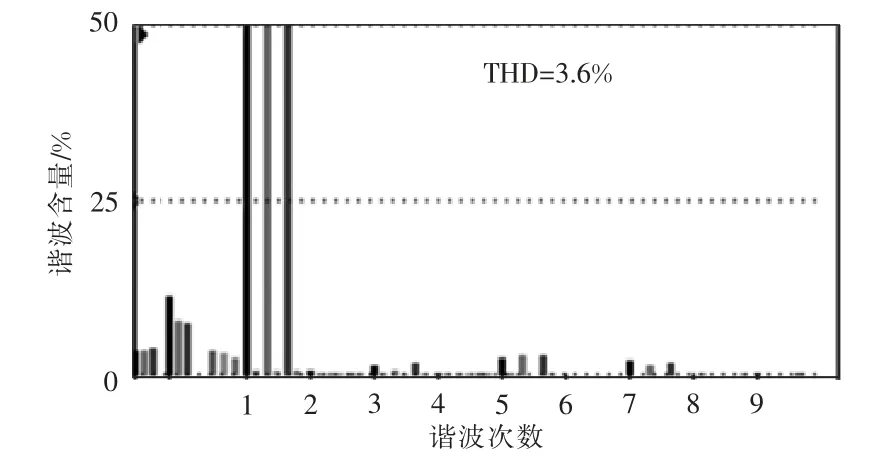
图11 基于SOGI-FLL 的准PR 控制器THD 值Fig.11 THD value of quasi-PR controller based on SOGI-FLL

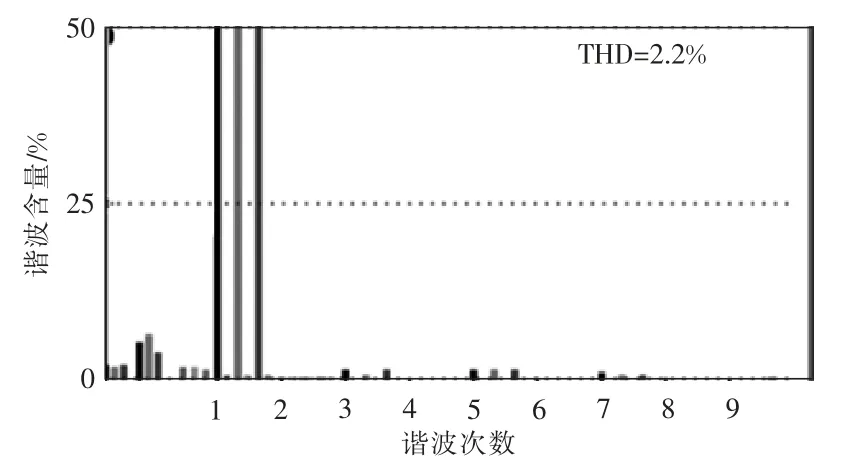
图12 基于LKF-FLL 的准PR 控制器THD 值Fig.12 THD value of quasi-PR controller based on LKF-FLL

4 结论

针对LCL 型滤波器的三相并网逆变器，本文提出了一种基于LKF-FLL 的PR 控制方法，经仿真和实验得出以下结论：

（1）本文所提设计方案将谐振控制与LKF-FLL结合，实现了频率自适应，加强了系统对电网频率偏移的适应能力。

（2）讨论分析了卡尔曼滤波器的参数选取，弥补了FLL 在追求快速响应过程中的抗干扰问题。

（3）通过仿真和实验证明了LKF-FLL 对电网频率的跟踪速度比SOGI-FLL 快，精度高，基于LKFFLL 的准PR 控制器能够兼顾动态性能和跟踪能力。

（4）比较研究2 种控制策略得到的并网电流THD，证明了基于LKF-FLL 的准PR 控制器对电网频率追踪能力以及对准PR 控制器的控制效果提升，并网电流的电能质量得到了改善。