微电网储能系统调度日SOC 初值确定方法

郑 健，杨 耕，耿 华

（清华大学自动化系，北京 100089）

微电网为满足并网和孤岛运行模式下的能量平衡问题，其控制/调度单元需要对光伏、风电、储能系统ESS（energy storage system）、柴油发电机等分布式电源DG（distributed generation）及可控负荷进行控制和管理。微电网调度的目标有经济性、可靠性等[1-3]。ESS 加入微电网后，可以提高新能源的消纳，提高供电的可靠性。同时，由于动力电池和变流器的成本目前比较高，ESS 成本也比较高，经济性和可靠性存在一定的对立关系。目前大规模的商用ESS 比较少见，且用于平抑波动较多，用于削峰填谷较少[4]。此外，新能源微电网中ESS 参与重要负荷保障时，相对柴油发电机而言具有无缝切换的优势。因此，对这类要求高可靠性的负荷而言，ESS 可以同时提高负荷运转的经济性和可靠性，在微电网孤岛运行的极端工况下，如何充分发挥ESS 的作用成为微电网调度的一个关键问题。

ESS 的容量和荷电状态SOC（state of charge）决定了ESS 在未来一段时间内能够存储或使用的能量。在以天为时间长度的调度中，每天ESS 的SOC初值决定了当日ESS 供电和吸收富余能量的能力，进一步影响新能源消纳、传统能源出力以及微电网应对峰值负荷的能力，对微电网运行的经济性和可靠性影响很大。例如，当某一调度日新能源出力大，微电网能量富余时，希望ESS 的SOC 初值低，可以多存储能量，以提高经济性；当调度日微电网能量不足时，希望ESS 的SOC 初值高，以保证该调度日的能量需求，提高系统可靠性。ESS 的加入还使得微电网每日的调度成为一个连续的过程，调度日之间通过ESS 的SOC 变化紧密联系[5]。因此，每天ESS的SOC 初值确定，既要考虑多日工况对该值的需求，也要考虑前一日的调度计划，是微电网调度中的重要环节。在目前对微电网调度的研究中，通常将ESS 每天的SOC 初值设定为常值（例如50%），并将一天结束时SOC 的终值控制到初值作为调度模型的一个约束，使得每日的SOC 初值保持不变[3，9]。这个约束简单实用，但由于每日新能源发电量和负荷情况会发生变化，对储能系统SOC 初值的需求也不相同，该方法在经济性和可靠性上就略显不足。

本文提出一种微电网储能系统调度日SOC 初值的确定方法。首先，综合多日调度下工况的数据分析对ESS 每天SOC 初值的不同需求；其次，在调度模型中引入每日SOC 终值下限约束，并根据多日工况对ESS 的能量需求给出该下限值；再次，通过多时间尺度的调度方法确定ESS 调度日的SOC初值；最后，通过一个通用的微电网模型对该方法进行验证。

1 微电网孤岛运行下ESS 需求分析

典型微电网结构如图1 所示，微电网与公共电网通过公共连接点PCC（point of common coupling）连接，当PPC 断开时微电网孤岛运行。每个调度周期调度中心调度网内所有设备给网内负荷、新能源、备用电源、ESS 发送功率指令Pload，t、Pnew，t、Pbp，t、Pess，t，微电网保持功率平衡。在长时间尺度下，调度日还需要保持能量平衡。以d 表示调度日，是负荷需求的能量，是新能源、备用电源提供的最大能量；ESS 提供的最大能量是调度日的初始容量，取决于其初始SOC

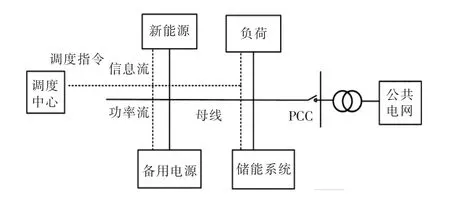
图1 典型微电网结构Fig.1 Typical structure of microgrid

由以上分析可以得出，d调度日对ESS 初始SOC 的最低需求为

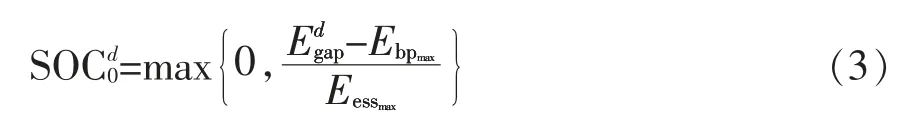
式（3）计算了单个调度日对于ESS 初始SOC 的最低需求，当考虑多个调度日后，微电网的工况变得更加复杂。每个调度日有（a）、（b）两种情况，考虑k 个调度日，则有2k种情况，复杂度呈指数增加。假设有n，n+1，…，n+k 个调度日，要考虑n+1，n+2，…，n+k 共k 个调度日的能量供需情况，计算第n+1 日对ESS 初始SOC 的最低需求。

首先，考虑的调度日数量k 不同，多日的能量缺口叠加使得在n+1 日考虑的多日总能量缺口不断变化，则有

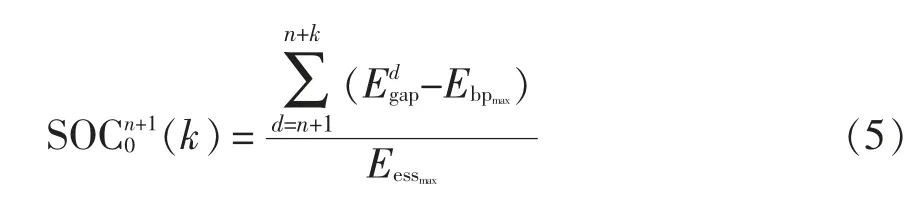
由于在k 个调度日中，后面调度日的能量是不能在前面调度日使用的，因此，并不能简单地将k个调度日的能量供需叠加起来计算最低需求，应该取中的最大值，即

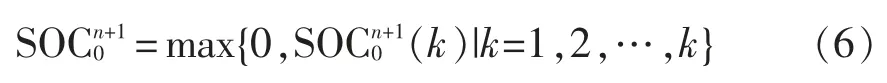
通过式（5）和式（6）可知，考虑k 个调度日内能量供需情况下，对n+1 日ESS 初始SOC 的最低需求。一般情况下，希望这个最低需求总是能够满足，然而ESS 的SOC 是连续变化的，与每个调度周期t的功率指令相关联，其关系分别表示为

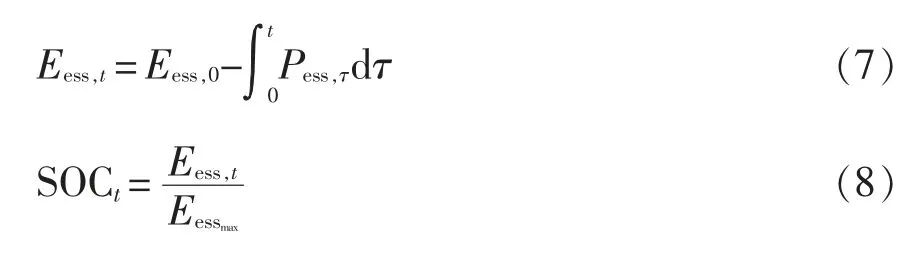
因此，n+1 日ESS 的初始SOC 继承第n 日的最终SOC，还需要考虑第n 日的能量供需情况。如果第n 日的能量能够满足第n+1 日的最低需求，则在此基础上制定调度计划；如果不能满足，只能根据能量供需情况，使第n+1 日的初始SOC 最大，表示为

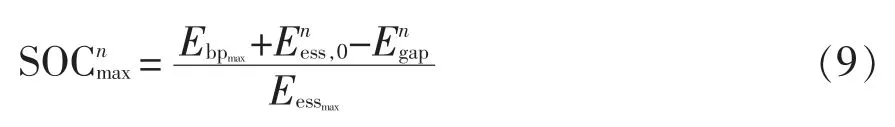
2 功率预测和调度

由上述分析可知，第n+1 调度日ESS 的SOC初值取决于n+1，n+2，…，n+k 调度日的需求以及第n 调度日的调度计划。这需要对未来n+1，n+2，…，n+k 日的发电和用电进行有效预测，以及对第n 日准确调度。

2.1 基于预测的多时间尺度调度方法

以光伏发电预测为例，文献[11]中基于多元线性回归理论对光伏发电进行了多时间尺度的预测。该方法不仅基于定性变量（小时、月份、天气类型）和定量变量（光照强度）设计了光伏发电功率预测模型，而且基于当前的实际发电量设计了短时间尺度的矫正环节。在复杂气象条件下进行的仿真结果显示，矫正环节将预测结果的平均绝对百分比误差由0.543 3 减小到0.162 4，能够显著改善单一依赖于预测模型的功率预测精度。

与之对应，调度环节也可以进行更为准确的实时调度。图2 说明了多时间尺度预测与调度的关系。

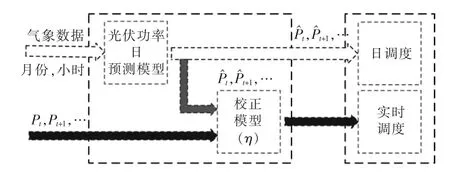
图2 多时间尺度光伏功率预测与调度的关系Fig.2 Relationship between multi-timescale photovoltaic power forecasting and scheduling

在短时间尺度上，不断更新预测数据，根据新的数据进行实时调度，不断修正调度计划，整个过程如图3 所示。

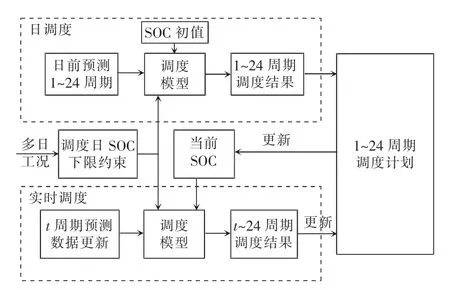
图3 多时间尺度调度过程Fig.3 Process of multi-time scale scheduling

2.2 考虑多日工况对ESS 需求的调度模型

基于上述多时间尺度预测方法进行实时调度时，对调度算法的实时性要求很高。本文采用凸优化调度方法[9-10]，这种方法不但求解速度快，还可以得到全局最优解。

假定微电网孤岛运行，以1 h 为调度周期，每个调度日共24 个调度周期，t=1，2，…表示调度周期。

假定新能源的发电成本为0，所以目标函数中的发电成本只包括备用电源和ESS 的发电成本。优化目标为运行成本最小，目标函数为

式中：ak为第y 个备用电源的成本折算系数；bm、cm为第m 个ESS 充、放电成本系数，可以根据不同体系电池的特性和成本价格差异进行调整；h 为网损折算系数；rl为第l 条支路的电阻。

约束条件包括微电网的潮流约束、发电设备约束、ESS 约束，潮流约束和发电设备约束。参考文献[9]，本文研究ESS 的SOC 初值确定方法主要与ESS相关的约束为

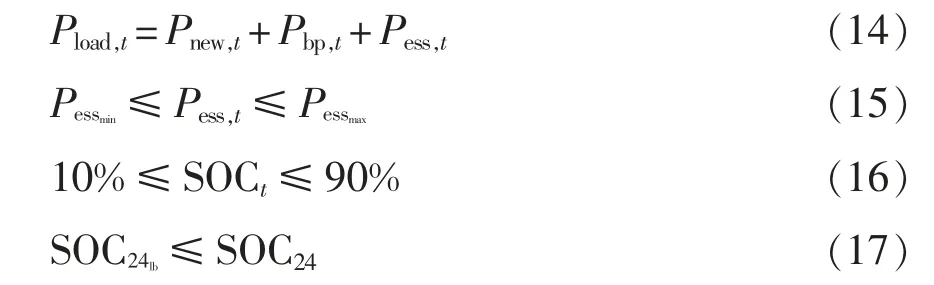
式中：SOC24为调度日SOC 的最终值；为调度日SOC 的终值下限。式（14）是微电网瞬时功率平衡的约束；式（15）是ESS 的最大充、放电功率约束；式（16）是为了保证ESS 运行过程中SOC 在安全范围内的SOC 上下限约束[12]；式（17）是对调度日ESS 的SOC 终值进行约束，可以根据多日工况对ESS 的需求获得。

3 储能系统调度日SOC 初值的确定

基于多日的微电网工况分析和多时间尺度调度方法，可以确定每个调度日的ESS 初始SOC，假定有n，n+1，…，n+k 个调度日，考虑2 d 能量供需情况，整个过程如图4 所示。

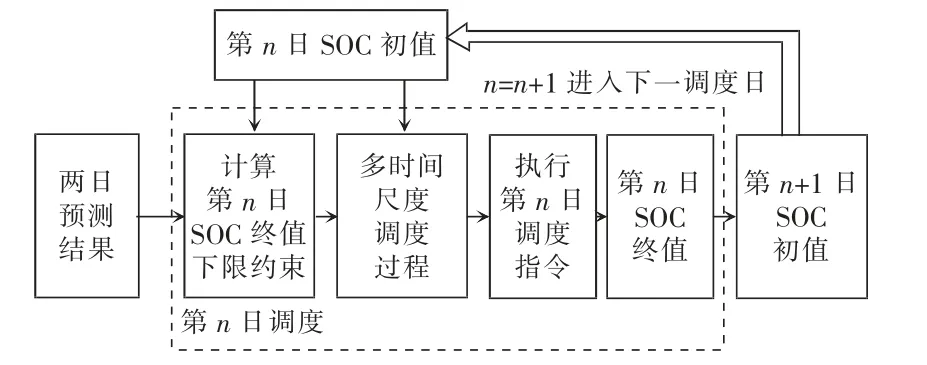
图4 储能系统SOC 每日初值确定方法Fig.4 Daily initial SOC determination method for ESS

具体步骤如下。

（1）计算调度日ESS 最终SOC 的下限约束。以第n 日调度为例，在得到2 d 预测结果和当日ESS的SOC 初值后，根据式（5）、式（6）、式（9）可以分别计算第n+1 日对初始SOC 的最低需求和第n 日能够提供的SOC 最大值。当时，两日总能量够用，可以满足最低需求；否则，只能按提供能量，而第n+1 日必须切除部分负荷。由此，可以得到第n 日ESS 最终SOC 下限约束为

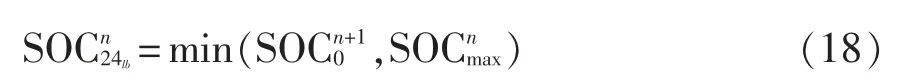
通过以上两步，在完成第n 日调度的同时，确定了第n+1 日ESS 的SOC 初值，可以继续进行第n+1 日的调度。

4 算例分析

本文选用的微电网来自国际大电网组织CIGRE（Conseil International des Grands Réseaux Électriques）推荐的Benchmark[13]，其结构如图5 所示。电网电压为20 kV，包含11 个节点和10 条支路，运行在孤岛状态。每个节点连接的DG、负荷情况和线路阻抗见表1。

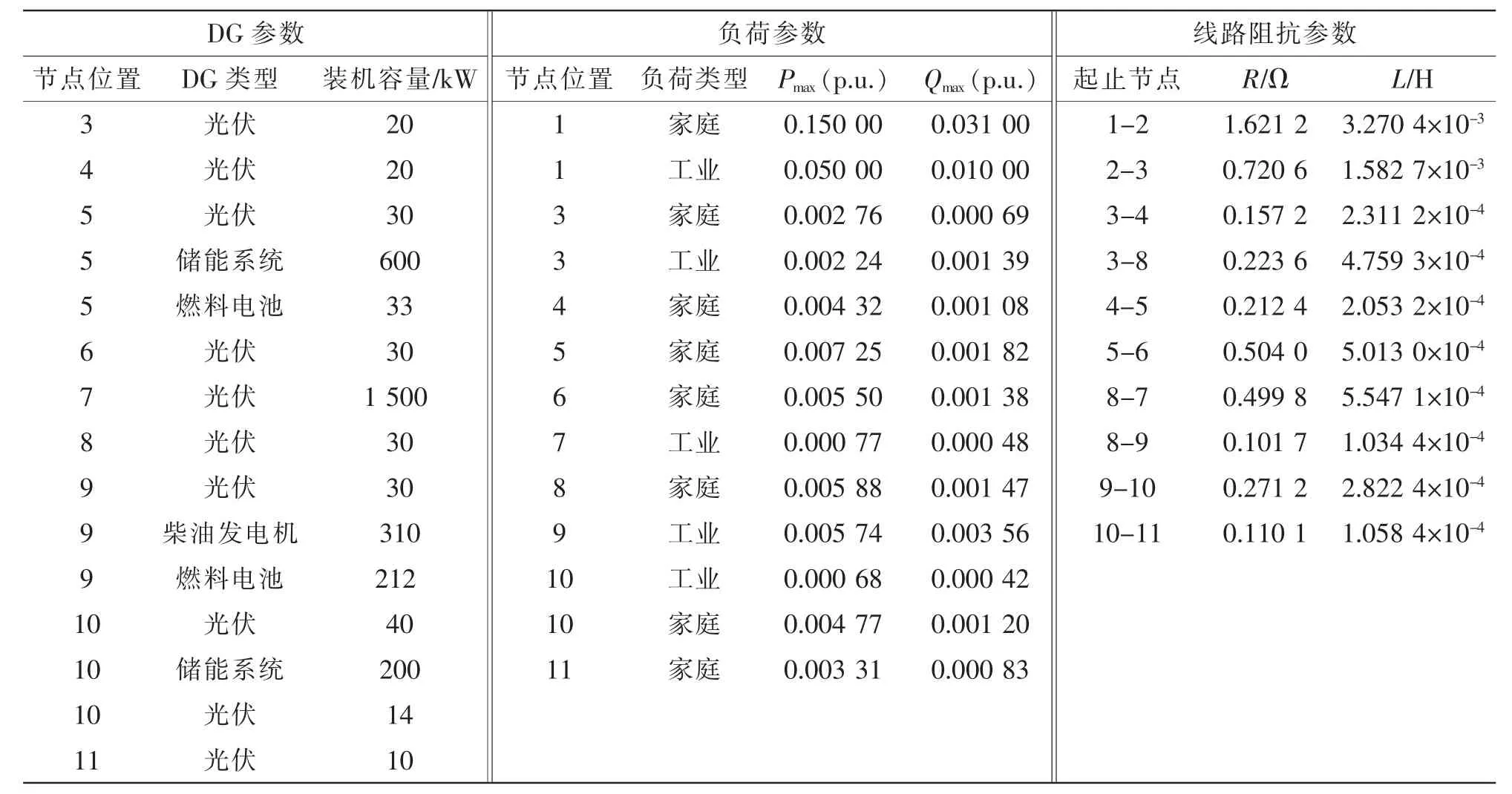
表1 微网相关参数Tab.1 Related parameters of microgrid

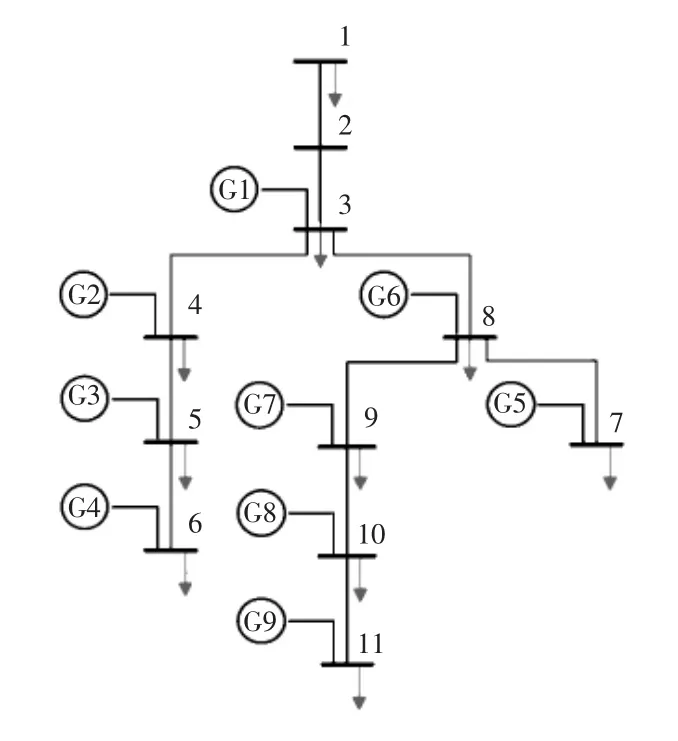
图5 微电网Benchmark（孤岛运行）Fig.5 Microgrid Benchmark（islanded operation）

本文设计的微电网采用两级分层控制架构[3]，底层的新能源发电装置采用虚拟同步机控制，而整个微电网采用一个集中控制器做全网的控制和调度。各层控制器已经保证微电网的稳定性，集中控制器采用第2 节的多时间尺度调度方法进行调度。

在仿真中，以2 d 调度为例，设计了2 种不同的工况，采用本文所提方法对第n 日和第n+1 日进行调度。比较方案则采用ESS 约束为SOC0=SOC24=0.5 的调度方案，验证本文方法对微电网经济性和可靠性的影响。

4.1 工况1：第n 日新能源发电量富余

工况1 模拟第n 日新能源发电量有富余，而第n+1 日需求这部分能量的情况。因此，调度模型中ESS 约束为≤SOC24，根据式（18）计算得第n日2 个ESS 最终SOC 的下限约束为0.374。仿真结果如图6 所示。

工况1 的仿真中，采用2 种方法的共同点是2个调度日后，2 个ESS 的SOC 都回到了0.5。不同之处在于，采用约束SOC0=SOC24=0.5 时，如图6（a）所示，第n 日的光伏能够按照最大功率输出，但是风机出现了弃风现象，调度的总成本为5 889.7 元；而采用本文方法，通过改变约束，使得第n+1 日2 个ESS 的SOC 初始值分别为0.86、0.70，第n 日多出的能量存入了ESS，风机不再弃风，调度的总成本为5 498.7 元，降低了6.64%。所以本文方法提高了新能源的利用率，经济指标更好。

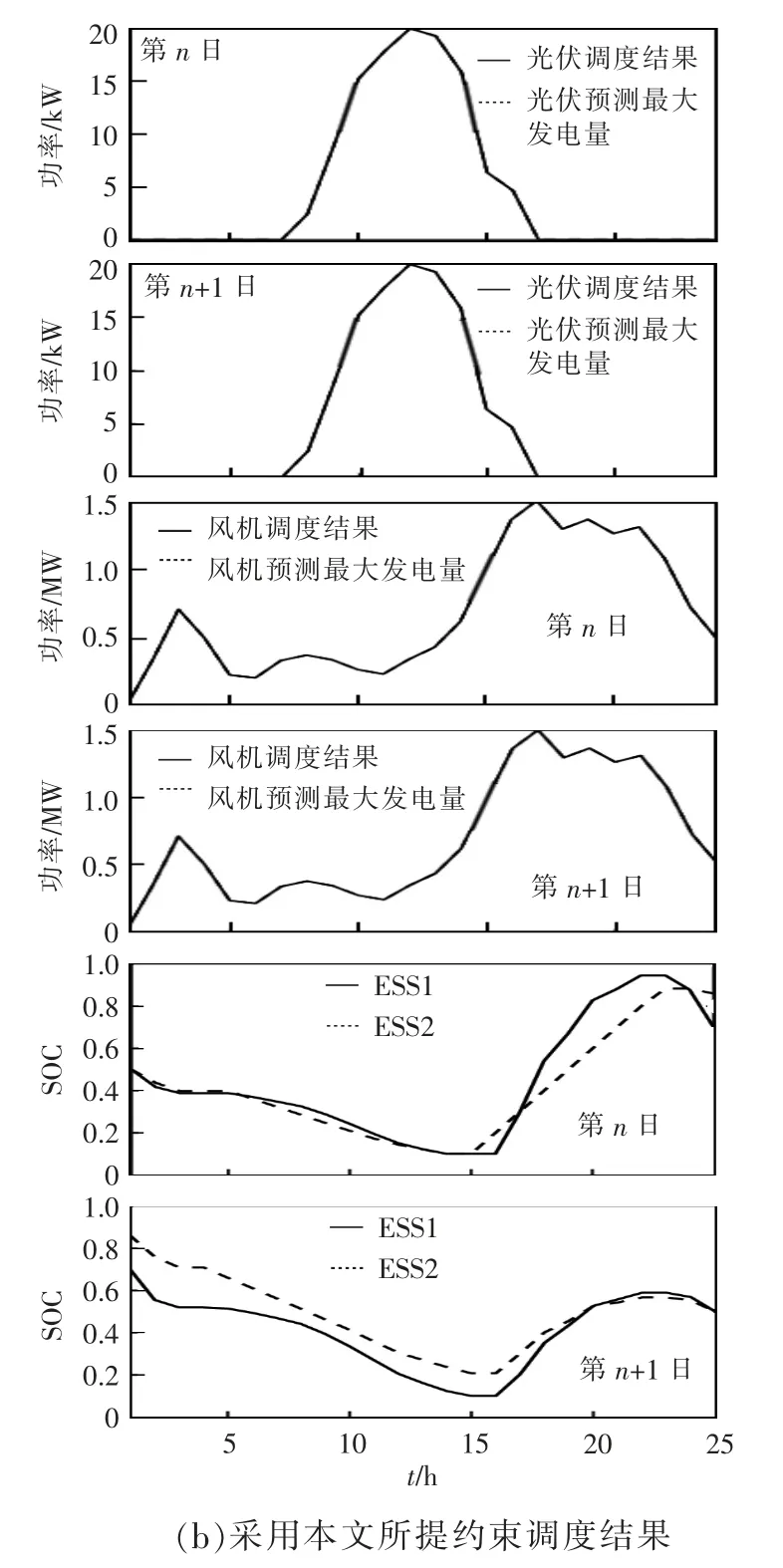
图6 工况1 仿真结果Fig.6 Simulation results in Condition 1

4.2 工况2：第n、n+1 连续两日新能源发电量都不足

工况2 模拟第n、n+1 连续两日新能源发电量都不足的情况，且第n+1 日能量缺口较大，备用电源无法填补缺口，需要ESS 提前存储足够的能量。

比较基准依然是ESS 约束SOC0=SOC24=0.5。使用本文方法，调度模型中ESS 约束为，根据式（18）计算得第n 日两个ESS 最终SOC 的下限约束为0.711。仿真结果如图7 所示。

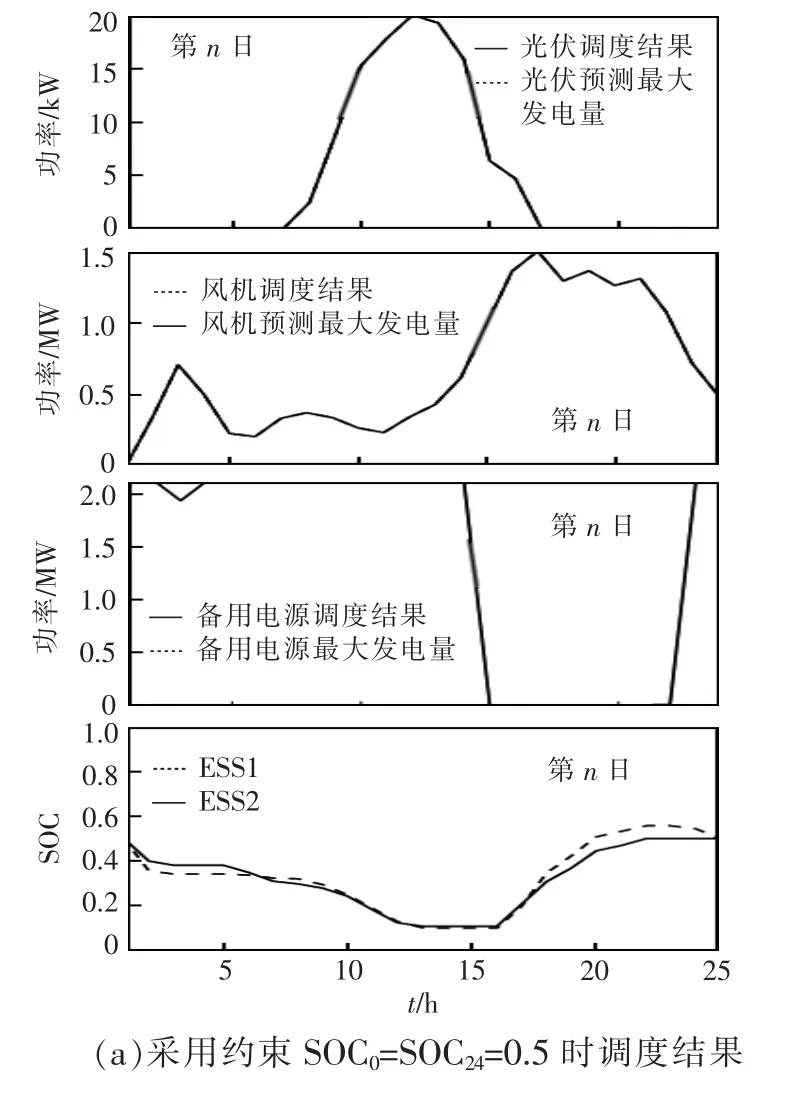
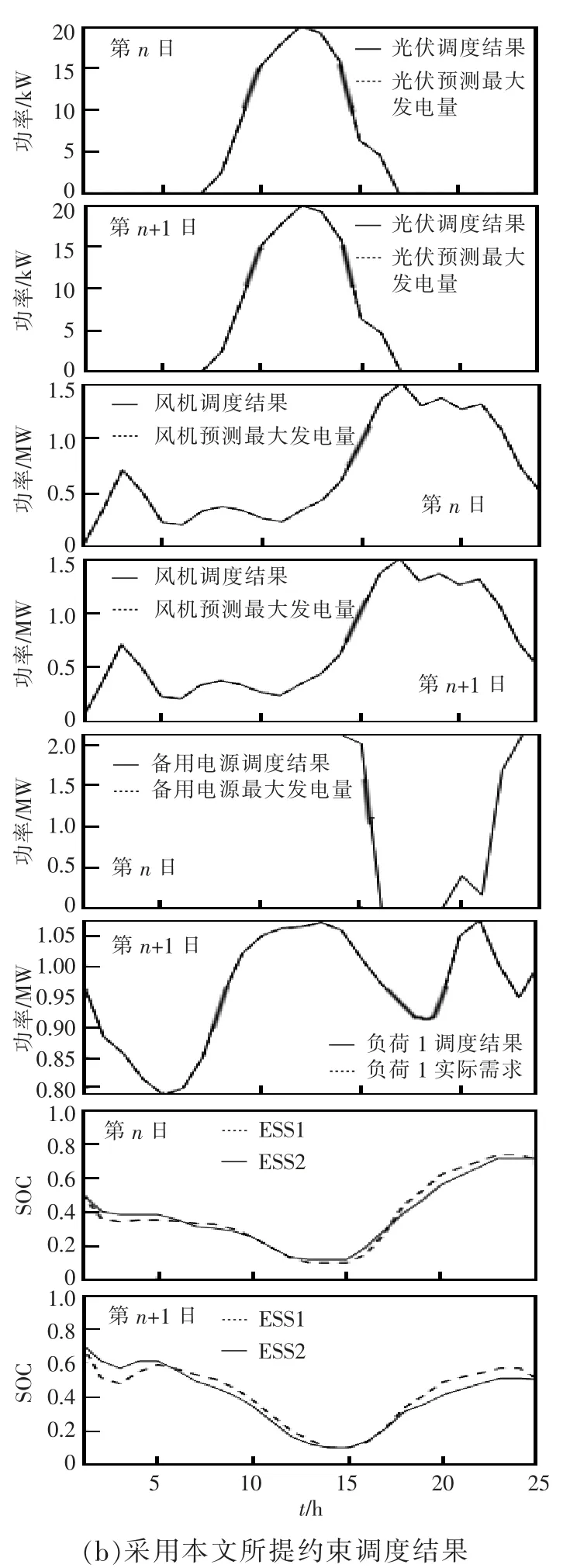
图7 工况2 仿真结果Fig.7 Simulation results in Condition 2

由仿真结果可知，ESS 约束SOC0=SOC24=0.5时，虽然第n 日调度计划能够使光伏、风电按最大功率输出，但是由于只考虑了当日的使用需求，没有给ESS 多充电，无法满足第n+1 日的负荷需求。所以第n+1 日只能切除部分负荷。采用本文方法后，使第n 日增加了备用电源的出力，提前给ESS充电，虽然第n 日发电成本增加了，但是保证了第n+1 日2 个ESS 的初始SOC 均为0.711，能够满足第n+1 日的负荷需求，提高了供电可靠性。

5 结论

（1）调度模型中引入每日SOC 终值下限约束，并根据多日工况对ESS 的能量需求给出该下限值。

（2）基于多时间尺度功率预测技术和调度方法的日调度计划。该调度不但可以使ESS 的运行满足当日功率平衡需求，还能实现所计划的次日SOC初值目标。

（3）本文采用微电网的一个Benchmark 进行了两日调度仿真，结果表明SOC 初值的合理设定提高了微电网的经济性和可靠性。