计及开关频率分区优化的PMSM 三电平模型预测控制

朱晨光，於 锋，罗 潇，吴晓新

（1.南通大学电气工程学院，南通 226019；2.国网上海市电力公司，上海 200025）

模型预测控制MPC（model predictive control）是20 世纪70 年代后期开始受到研究者们广泛关注的计算机控制算法。在电机控制领域中主要分为模型预测电流控制MPCC（model predictive current control）和模型预测转矩控制MPTC（model predictive torque control）[1-3]。MPTC 通过价值函数在线滚动优化，来获取逆变器的最优开关状态，能够提高系统的动态响应，并在一定程度上减小转矩脉动。但是，由于磁链与转矩的量纲不同，在传统的MPTC 价值函数中需要加入权重系数对转矩跟踪和磁链跟踪进行权衡。然而，由于缺乏统一有效的设计方案，最优权重需要通过仿真和实验不断调试来确定，因此设计权重系数是一项十分繁琐的工作[4-5]。

随着电力电子技术的发展，一种二极管中点钳位式NPC（neutral-point-clamped）三电平逆变器因其更小的电压应力、更低的谐波含量等优点受到国内外研究者们的关注[6-8]。但是NPC 三电平逆变器需要在全工况下保持中点电位平衡才能稳定运行，因此，如何更好地控制中点电位，是应用NPC 三电平逆变器的关键技术问题。文献[9]提出一种基于正负小矢量的中点电位控制策略，即通过检测当前中点电位状态，利用正负冗余小矢量对中点电位作用效果相反的特性来对小矢量进行合理替换，从而有效平衡中点电位。此外，由于NPC 三电平逆变器存在27 个基本电压矢量，传统的MPTC 在一个采样周期内需要进行27 次运算，极大增加了控制器的计算负担，加剧了系统延时，降低了预测的准确性。因此，有必要通过减少备选矢量的数量来提高控制系统的性能。文献[10-11]提出一种磁链与转矩偏差的矢量筛选策略，通过分析不同电压矢量对磁链偏差的影响，以磁链偏差的绝对值最小为基准，将备选矢量由27 个减少到14 个，但并未在开关状态切换表中考虑开关频率的限制条件，可能会产生较高的开关频率，引起较高的开关损耗，降低系统效率和开关器件的使用寿命。为降低开关频率，文献[1]以线电压和相电压的幅值跳变均不超过直流母线电压的一半为原则，建立了能够降低开关频率的MPTC 有限控制集元素，同时也能够将备选矢量的数量筛选至4～7 个，然而7 个备选矢量仍然会给控制系统带来较大的计算负担。

针对上述问题，本文提出一种计及开关频率分区优化的永磁同步电机PMSM（permanent magnet synchronous machine）三电平模型预测磁链控制MPFC（model predictive flux control）方法。首先，采用文献[12]提出的控制策略，构建基于PMSM 的预测磁链控制模型以消除权重系数；进一步，提出一种分扇区优化的控制策略，在一个采样周期内仅允许一相开关状态发生连续跳变，并且根据上一时刻的开关状态仅选择相邻扇区内的基本电压矢量作为备选矢量，能够在降低开关频率的同时，有效地将备选矢量减少到3～5 个；然后，利用正负冗余小矢量进行中点电位平衡控制；最后，通过仿真与实验验证所提控制策略的有效性。

1 永磁同步电机数学模型的建立

本文以内嵌式PMSM 为研究对象，在dq 坐标系中建立数学模型。电机的定子电压方程和磁链方程分别为

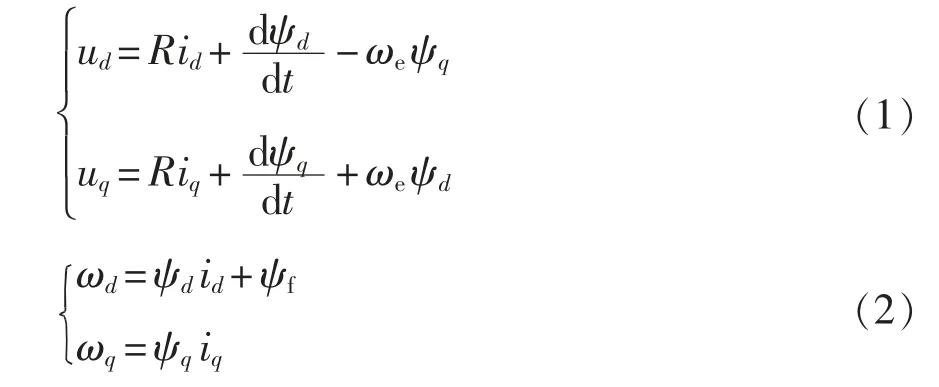
式中：ud、uq为d、q 轴定子电压分量；id、iq为d、q 轴定子电流分量；ψd、ψq为d、q 轴定子磁链分量；Ld、Lq为d、q 轴电感分量；R 为定子电阻；ωe为电角速度；ψf为永磁体磁链。

将式（2）代入式（1）得到新的定子电压方程为

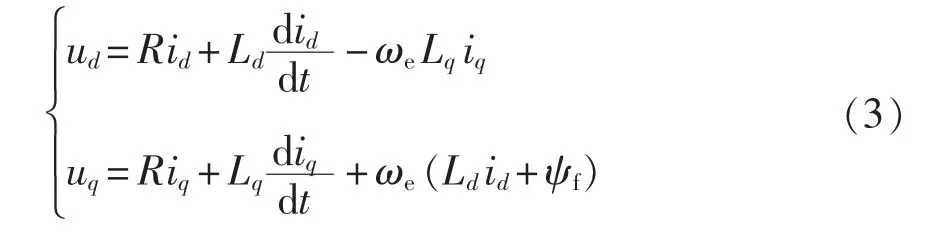
电磁转矩方程为

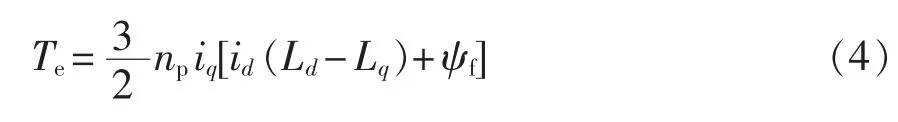
式中：Te为电磁转矩；np为极对数。

2 模型预测磁链控制

本文采用有限集模型预测控制算法，根据变换器的被控量x 和开关函数S 间的关系构建离散预测模型，再由k 时刻被控量的测量值和不同开关状态Sj（j=1，2，…，27）来计算k+1 时刻被控量的预测值，然后根据系统特性构建系统优化的价值函数g，最后通过价值函数的遍历、寻优挑选出使g 最小的开关状态Sj，直接作用于变换器。

2.1 模型预测磁链控制框图

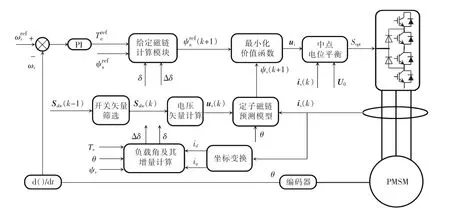
图1 NPC 三电平逆变器MPFC 框图Fig.1 Block diagram of MPFC scheme utilized in NPC three-level inverter

2.2 预测磁链控制模型

整理式（3）得dq 坐标系下的电流微分方程为

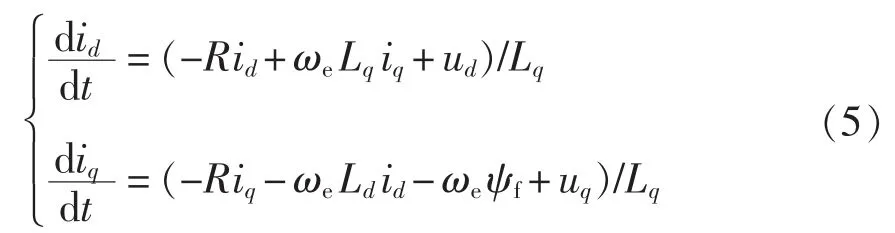
欧拉公式为

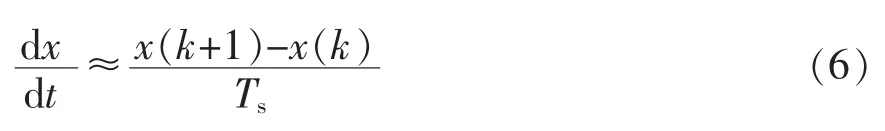
式中：x（k）和x（k+1）分别为当前k 时刻采样状态和k+1 时刻的预测状态。

将式（5）、式（6）经离散化处理可得k+1 时刻dq 坐标系下的电流预测方程，即

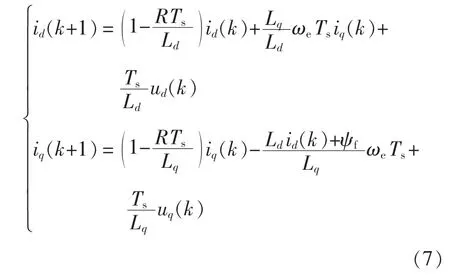
式中：id（k+1）、iq（k+1）为k+1 时刻d、q 轴的电流预测值；id（k）、iq（k）为k 时刻d、q 轴电流测量值；ud（k）、uq（k）为k 时刻d、q 轴定子电压分量；Ts为采样时间。

将式（7）代入式（4），可得k+1 时刻转矩的预测值Te（k+1）为

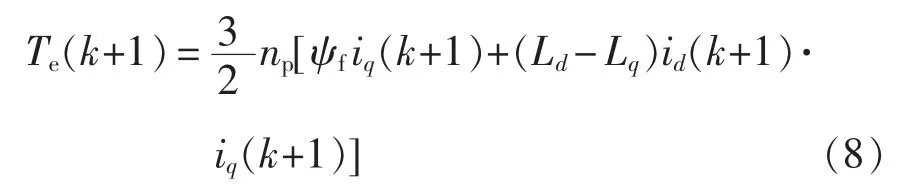
将dq 坐标系下的定子磁链方程用负载角函数表示为

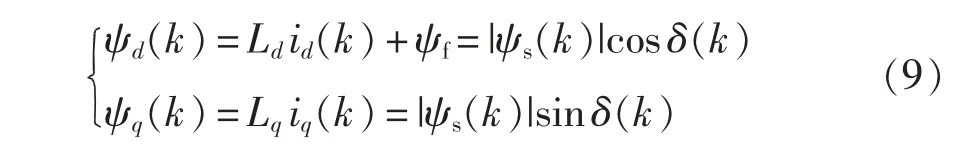
式中：|ψs（k）|为k 时刻合成磁链的幅值；δ（k）为k 时刻合成磁链ψs（k）与d 轴之间的负载角。

将式（9）代入式（4），再对δ（k）求导，并改写为增量形式，整理后可得负载角增量Δδ 方程为

根据式（9）和式（11）可得k+1 时刻d、q 轴磁链参考方程为

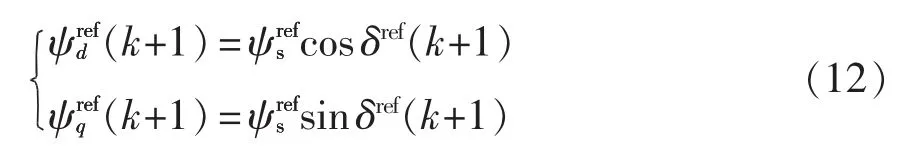
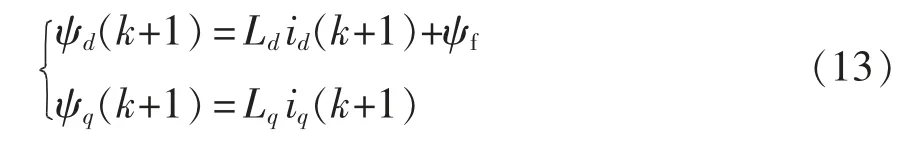
通过上述预测磁链控制模型的建立，将传统MPTC 中对转矩和磁链的控制转换为对d、q 轴磁链的控制，然后，基于磁链偏差最小的原则，k+1 时刻磁链的预测值应该尽可能接近磁链的参考值，即min{（k+1）-ψs（k+1）}，因此，可以建立MPFC 价值函数，即

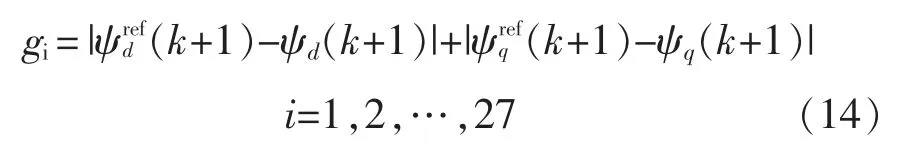
通过最小化价值函数，能够获得使式（14）最小的电压矢量作为控制输出。由式（14）可以看出，MPFC 的价值函数中仅包含磁链项，因此不需要权重系数的调节。

2.3 分扇区优化控制策略

图2 为NPC 三电平空间电压矢量分布。由于NPC 三电平逆变器存在27 个空间电压矢量，如果依次进行滚动优化，需要进行27 次运算，尤其是在多步及多矢量预测控制中，计算量会呈指数形式递增，这将影响预测控制的准确性。因此，为降低系统的计算负担，提出一种分扇区优化的控制策略。在一个采样周期中仅允许一相开关状态发生连续跳变，即开关状态仅允许在-1 和0 或0 和1 之间变换，在此基础上，仅考虑上一采样时刻作用矢量相邻扇区内的基本矢量作为备选矢量，能够在限制开关频率的同时进一步将备选矢量减少到3～5 个。

为降低开关频率的同时能够进一步减少备选矢量的数量，进行如下两步操作：

步骤1为降低开关频率，建立了开关频率约束条件，在每个采样周期只允许一相开关状态发生连续跳变，能够将备选矢量的数量减少到4～7 个；

步骤2考虑到7 个备选矢量依然是一个较大的计算负担，为进一步减少备选矢量的数量、降低计算负担，将空间电压矢量平面以30 度为界划分为12 个扇区，每个扇区有3 个零矢量、2 个小矢量、1 个中矢量和1 个大矢量，如图2 所示。

此时，计算模型属于超静定梁模型，求解时需要引入变形协调条件以及力与位移间的物理关系建立补充方程，具体方法简述如下。

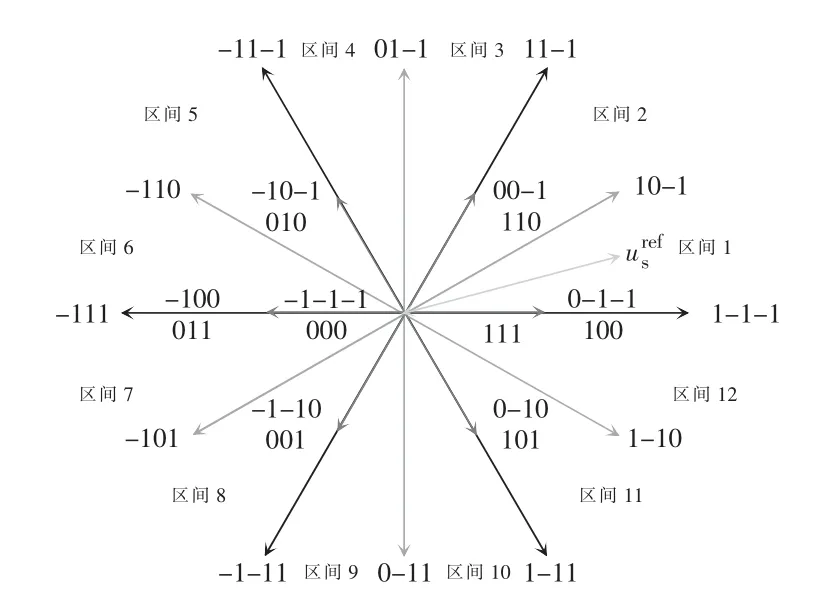
图2 NPC 三电平逆变器空间电压矢量分布Fig.2 Distribution of space voltage vectors of NPC three-level inverter

由于5 kHz 的采样频率下系统的采样周期仅0.2 ms，因此，在一个采样周期内参考矢量的位置变化不会超出上一采样周期内作用矢量的相邻扇区。所以，以上一时刻采样周期内的作用矢量为参考，选择相邻扇区内的矢量作为备选矢量，可以进一步将备选矢量减少至3～5 个，并且在理论上可以保证系统性能。以上一时刻的开关状态100 为例，相邻扇区为扇区1 和扇区12，在开关频率约束条件下的备选矢量为①100；②000；③1-10；④10-1。依此类推，可得分扇区优化矢量筛选表，如表1 所示。特别地，当上一时刻作用矢量为零矢量时，相邻扇区位置难以判断，因此，对零矢量-1-1-1 和111 仅考虑开关频率的限制，对于零矢量000 仅考虑开关频率的限制条件依然存在7 个备选矢量，为进一步减少备选矢量的数量，结合k+1 时刻参考矢量的位置进行进一步的筛选。

表1 分扇区优化矢量筛选Tab.1 Vector screening for subregion optimization

为判断参考电压矢量所在位置，首先对PMSM的三相电流ia、ib、ic进行Clark 变换得到αβ 坐标下的电流isα（k）、isβ（k），将式（2）进行反Park 变换得到αβ 坐标下的磁链ψsα（k）、ψsβ（k），则合成磁链与α轴之间的夹角为θs（k）=arctan（ψsα（k）/ψsβ（k））。

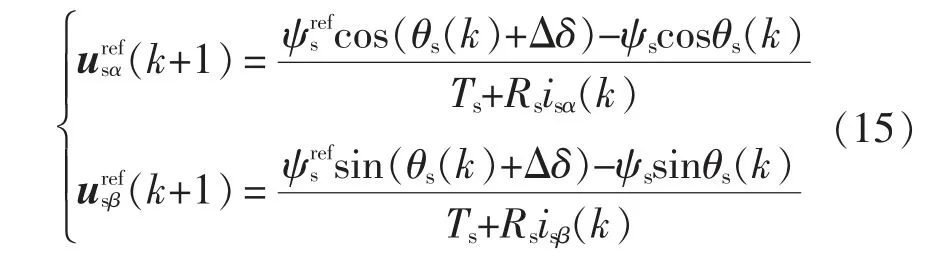
2.4 中点电位平衡

NPC 三电平PMSM 等效模型如图3 所示。通过对图3进行分析可知，NPC 三电平逆变器的空间矢量中，大矢量和零矢量不会对中点电位造成影响，仅有中矢量和小矢量会影响中点电位。利用一对冗余小矢量对中点电位的影响效果相反这一特性，当选择小矢量作为控制矢量时，通过检测当前中点电位的状态，选择有利于抑制中点电位波动的冗余小矢量进行替换，从而有效地控制中点电位。中、小矢量对中点电位的影响见表2。

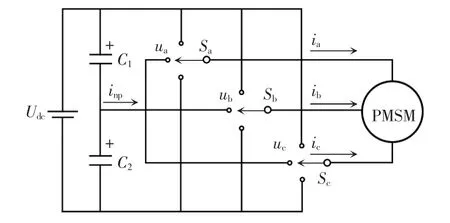
图3 NPC 三电平逆变器PMSM 等效模型Fig.3 Equivalent model of NPC three-level inverter based PMSM

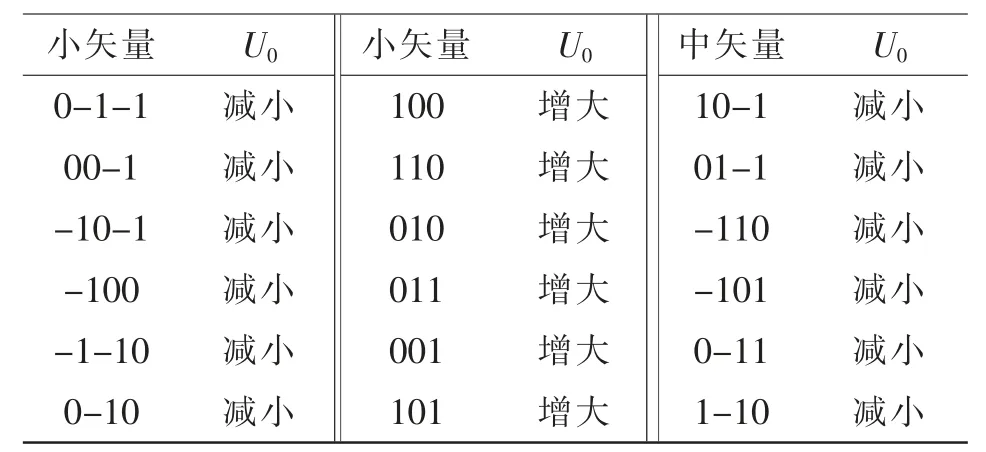
表2 中、小矢量对中点电位U0 的影响Tab.2 Effect of small and medium vectors on midpoint potential U0

通过上述分析可以看出，所提出的中点电位平衡控制方法是基于正负冗余小矢量实行的，因此，不需要将中点电位放入价值函数进行统筹考虑，也不需要繁琐的权重系数调节过程。实际上，所提出的中点电位平衡策略是在价值函数滚动优化之后进行的，当价值函数选择小矢量作为控制输出量时，判断当前中点电位的状态，若当前中点电位偏高则采用对应的负小矢量作为控制输出，若当前中点电位偏低则采用正小矢量作为控制输出。此外，在本文所提出的分扇区优化矢量筛选表中，每个备选矢量集均有小矢量的存在，这意味着任何一个备选矢量集参与运算均有可供选择的小矢量来平衡中点电位。

3 仿真分析

为验证所提出的计及开关频率分区优化的PMSM 三电平模型预测控制策略的可行性，利用Matlab/Simulink 软件对该算法进行了仿真。PMSM参数见表3。仿真中设置逆变器直流侧母线电压为300 V，逆变器直流侧上下分压电容为470 μF，系统采样频率为5 kHz。

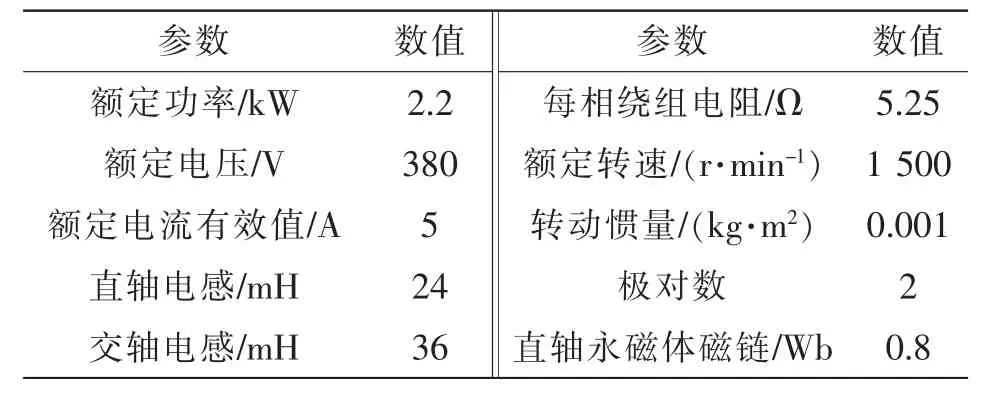
表3 PMSM 参数Tab.3 Parameters of PMSM

3.1 NPC 三电平线电压及中点电位

图4 为NPC 逆变器线电压仿真波形，可以看出，图4（b）所示的NPC 三电平逆变器线电压波形存在5 个电压梯度，而图4（a）所示的两电平逆变器线电压波形只有3 个电压梯度，因此NPC 三电平逆变器能够获得比两电平逆变器正弦度更好的波形。

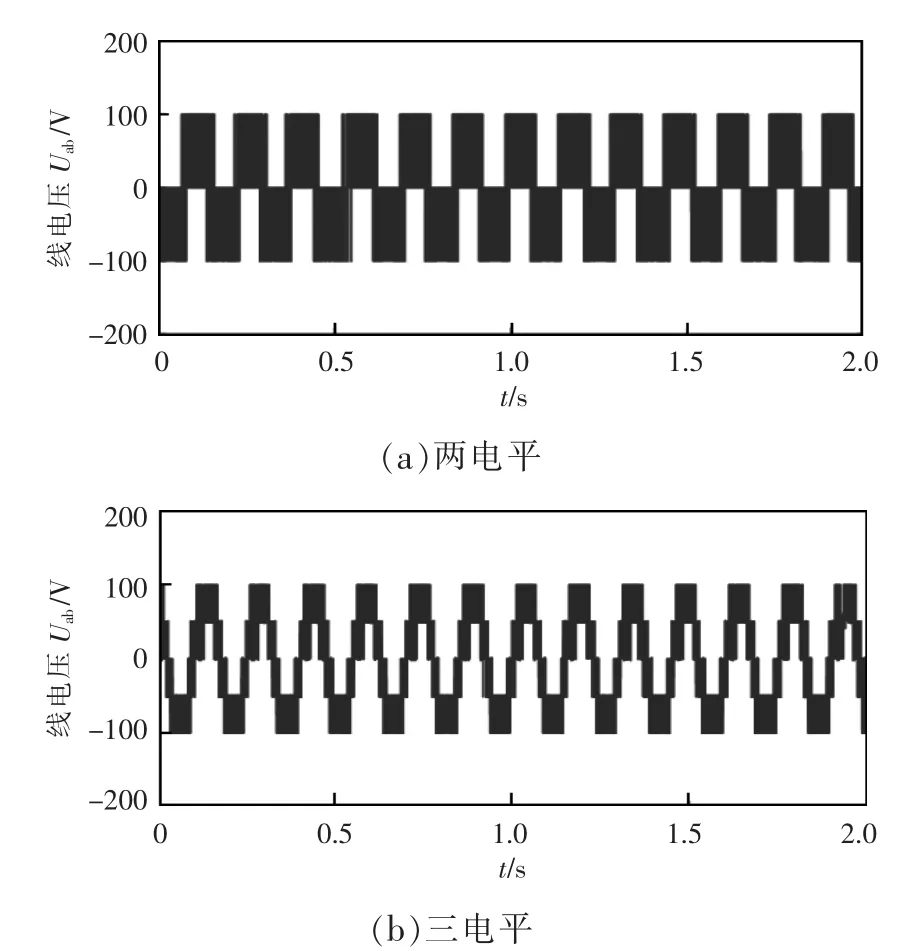
图4 NPC 逆变器线电压仿真波形Fig.4 Simulation waveforms of line voltage for NPC inverter

图5 为A 相电流和中点电位平衡仿真波形，在t=1 s 之前不进行中点电位的控制，此时，直流侧分压电容从t=0 时刻开始充电，由于开始阶段并未对中点电位进行平衡控制，因此，直流侧上下分压电容的充电速度并不一致，导致中点电位由0 缓慢上升到150 V，并使A 相电流波形发生严重畸变。在t=1 s 时刻加入中点电位平衡控制，此时，中点电位迅速下降且保持在0 附近，A 相电流波形能够保持较好的正弦度。

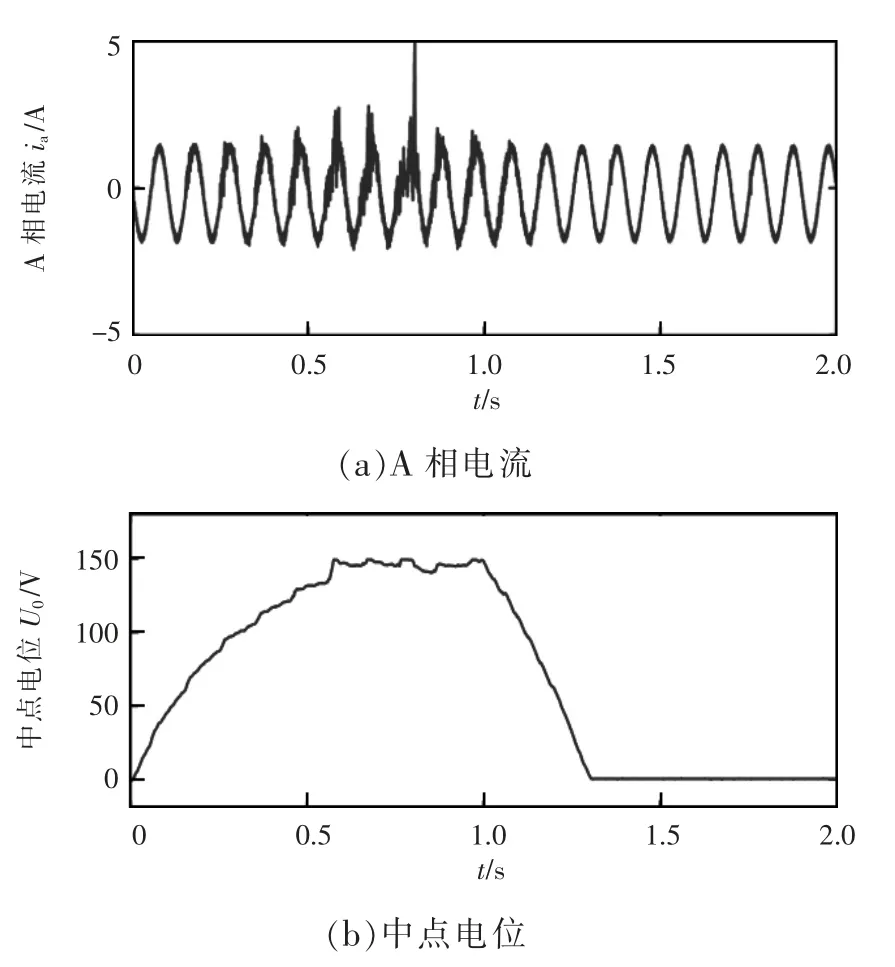
图5 A 相电流和中点电位平衡仿真波形Fig.5 Simulation waveforms in midpoint potential balance

考虑到随着调制比增大，参考矢量的长度也随之增大，小矢量的参与比例也随之减小，因此分别在调制比M=0.50、0.95 的条件下观察图6 所示中点电位的控制效果。在图6（a）调制比M=0.50 的条件下，中点电位能够很好地被抑制在0 附近，且基本不产生波动，证明在低调制比下所提出的中点电位平衡方法具有很好地控制效果；相比较于图6（a），图6（b）的中点电位控制效果明显变差，考虑到调制比M=0.95，参考电压矢量将接近电压极限圆运行，此时，小矢量的应用频率降低，导致中点电位产生较大的波动，但是中点电位依然能够被限制在0 附近，而且所提出的中点电位平衡控制方法不会对价值函数的滚动优化产生影响，也无需额外调节中点电位的权重系数。

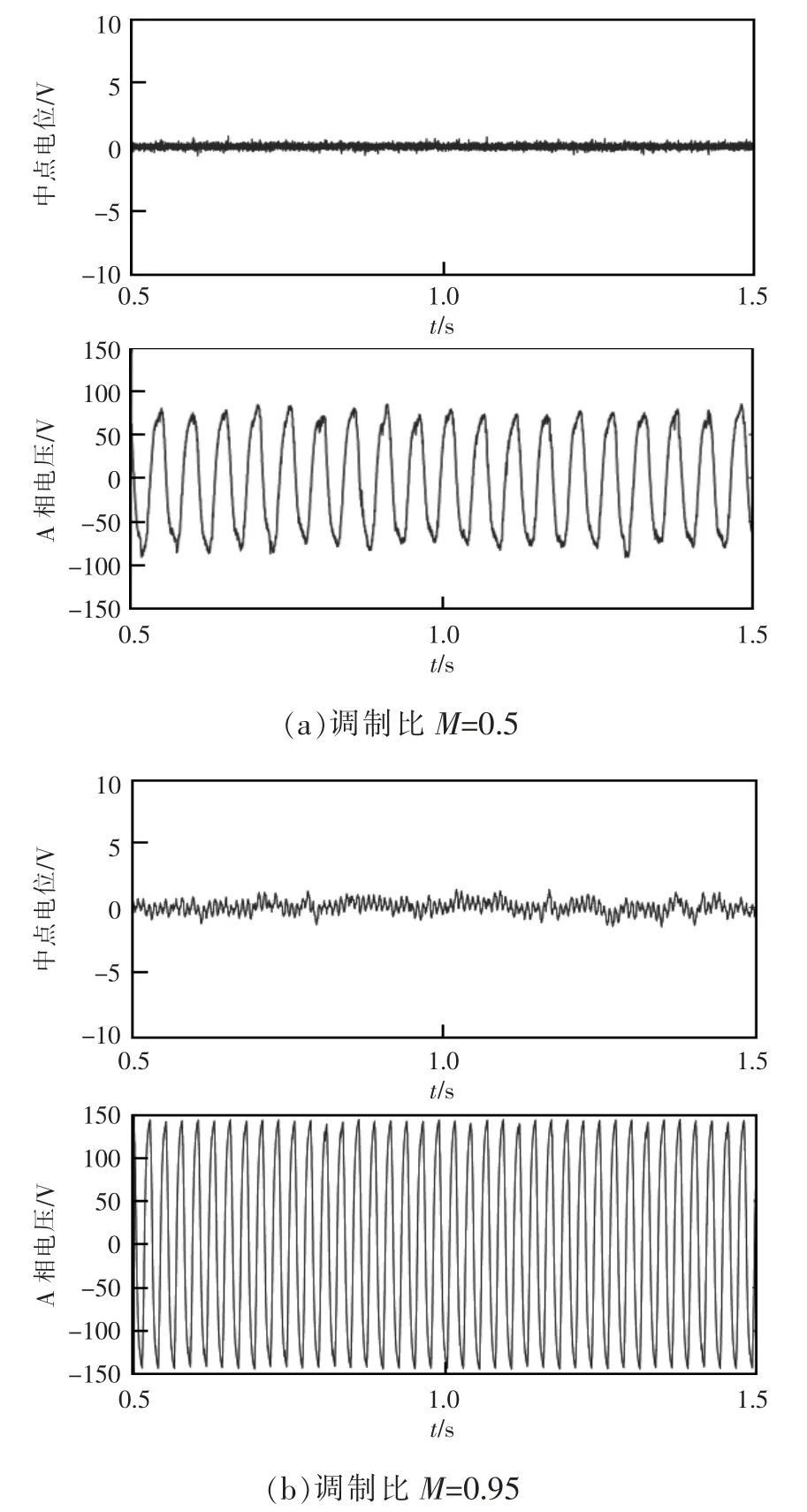
图6 不同调制比下的中点电位仿真波形Fig.6 Simulation waveforms of midpoint potential at different modulation ratios

3.2 稳态性能

图7 为分扇区优化的MPFC 稳态波形，在额定电压380 V、给定转速1 200 r/min、给定负载4 N·m的条件下进行稳态性能的仿真分析结果。可看出高速时转速和转矩均能够保持平稳，电流也能保持良好的正弦状态，中点电位也能够很好地被抑制在0附近，说明所提出的分扇区优化的NPC 三电平MPFC 方法在高速时依然能够获得良好的控制效果。

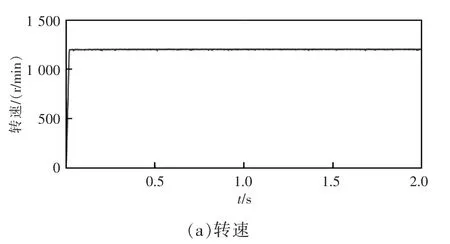
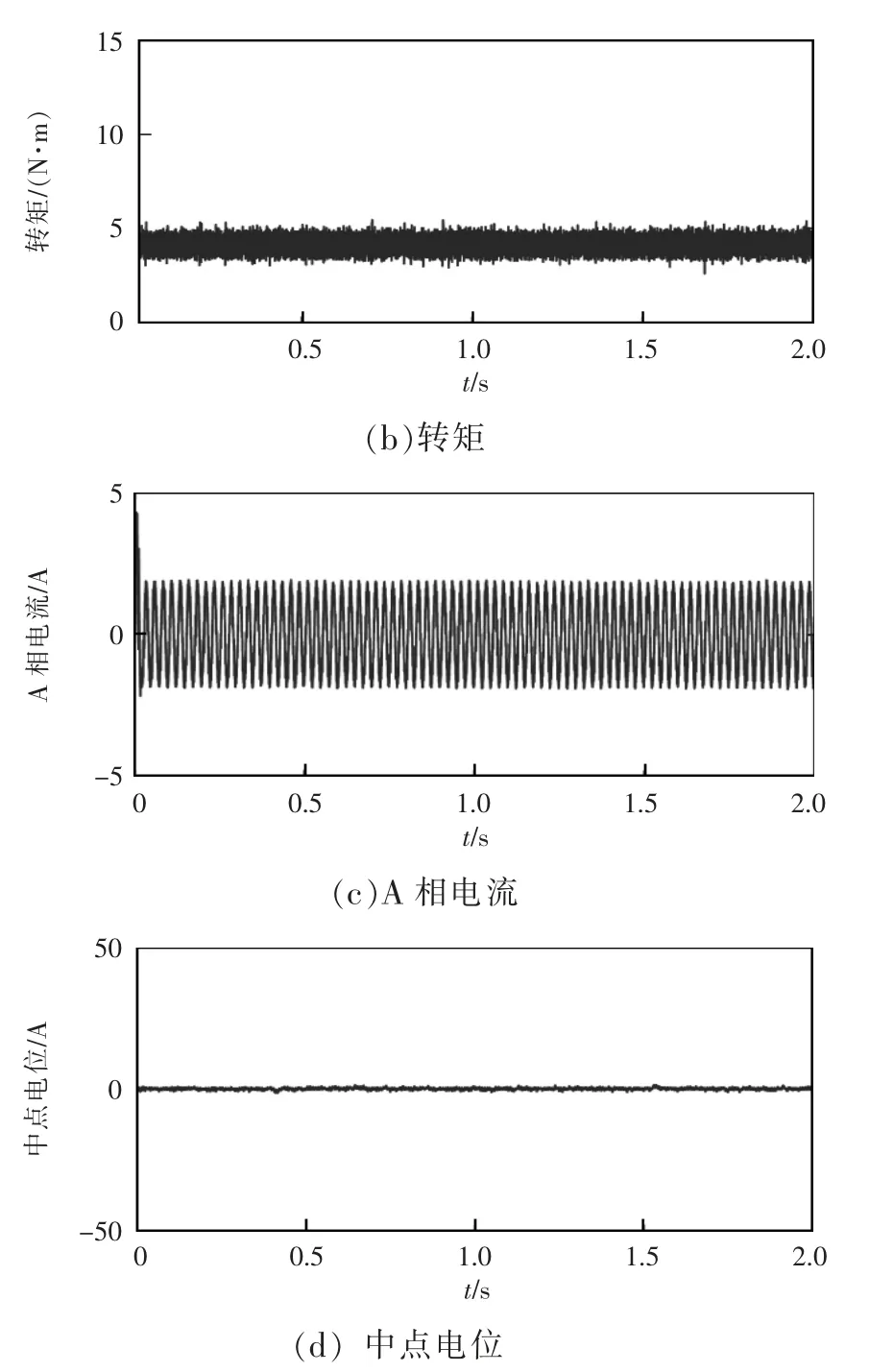
图7 分扇区优化的MPFC 稳态波形Fig.7 Steady-state waveforms of MPFC for subregion optimization

3.3 开关频率

图8 为给定转速300 r/min、负载转矩4 N·m 条件下开关频率仿真波形。图8（a）为不对备选矢量进行筛选的传统NPC 三电平MPFC 开关频率的仿真波形，开关频率达到4 kHz；图8（b）为文献[11]中基于磁链和转矩偏差开关状态表的仿真波形，开关频率为3.4 kHz；图8（c）为文献[1]中限制开关状态跳变的NPC 三电平MPFC 的仿真波形，开关频率为2.1 kHz；图8（d）为分扇区优化的NPC 三电平MPFC仿真波形，开关频率为2 kHz。通过对图8 的分析可知，比起传统MPFC 策略，文献[11]所提出的备选矢量筛选方法在减少备选矢量的同时，能够在一定程度上降低开关频率，文献[1]所提出的开关状态表能够在有效降低开关频率的同时将备选矢量减少至4～7 个，本文所提出的分扇区优化的控制策略能够比文献[11]更为有效地降低开关频率，而相比较于文献[1]能够在限制开关跳变的同时更为有效地减少备选矢量的数量。

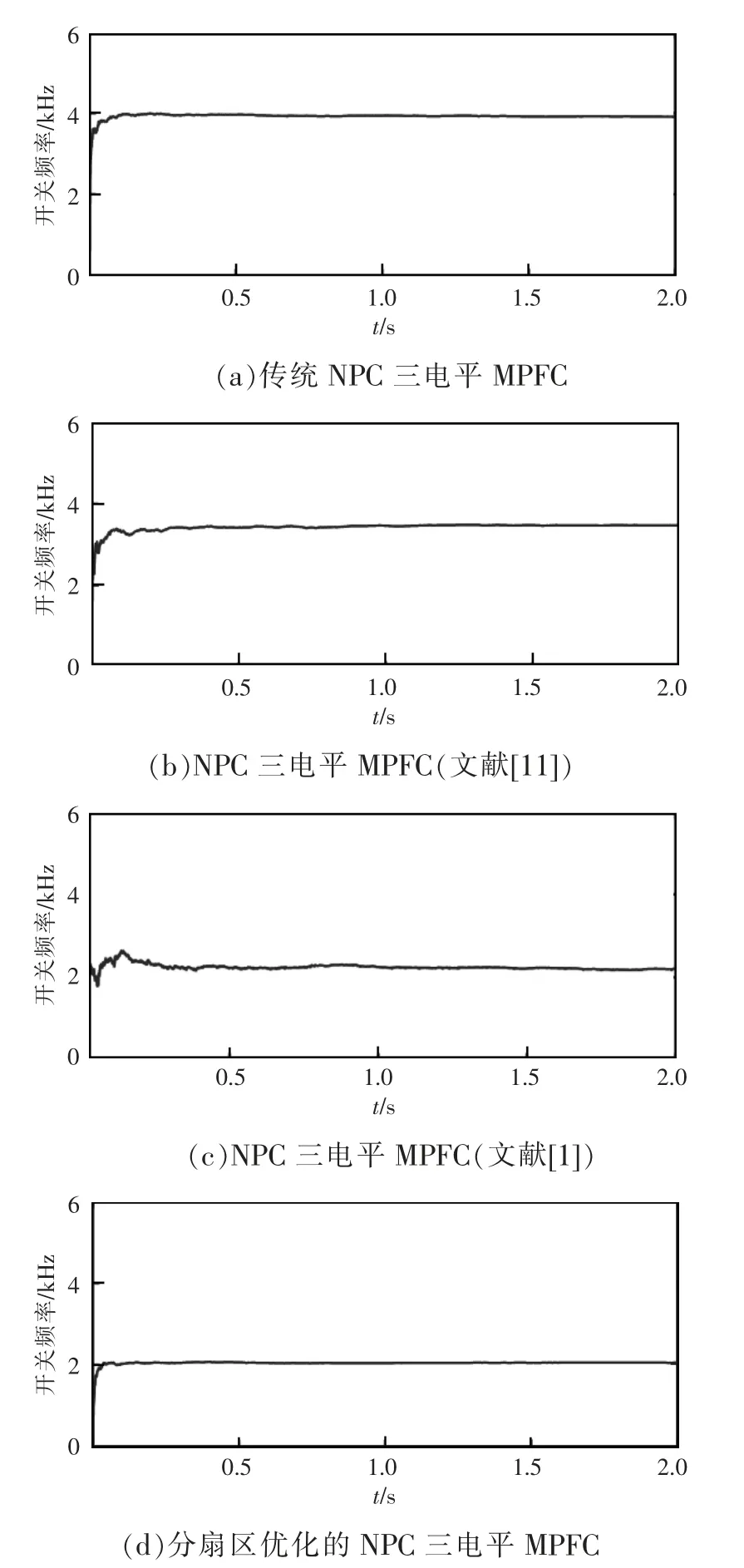
图8 开关频率仿真波形Fig.8 Simulation waveforms of switching frequency

4 实验验证

为验证所提出控制策略的可行性，以一台2.2 kW的PMSM 进行验证。实验平台如图9 所示，采用dSPACE1104 半实物平台，通过在Matlab 2009a/Simulink 环境下直接编译程序，生成dSPACE1104可识别代码，进而在dSPACE 软件中建立可调参数的虚拟界面进行实验分析。电机参数与表3 一致，直流母线电压300 V，采样频率5 kHz。

图9 实验平台Fig.9 Experimental platform

4.1 NPC 三电平线电压及中点电位

图10 为NPC 三电平线电压实验波形，可看出NPC 三电平逆变器线电压存在5 个梯度，能够获得较好的正弦度。

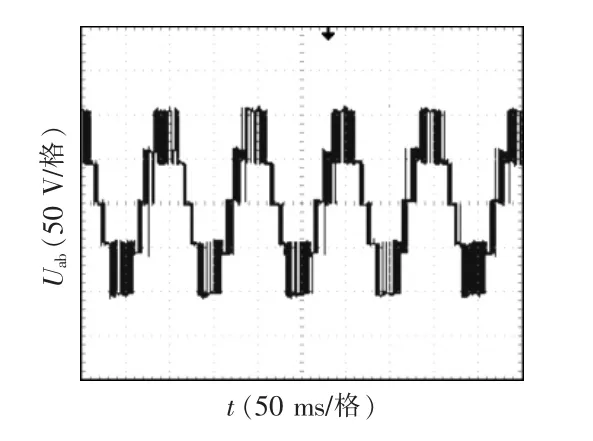
图10 NPC 三电平逆变器线电压实验波形Fig.10 Experimental waveforms of line voltage for NPC three-level inverter

图11 为NPC 三电平中点电位平衡实验波形，在加入中点电位平衡控制前，中点电位发生严重偏移，电流波形发生较大畸变；而加入中点电位平衡控制后，中点电位迅速稳定到0，电流波形也保持良好的正弦状态。

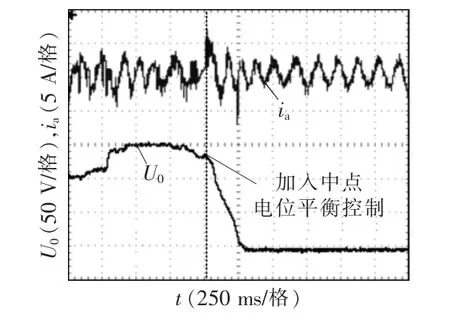
图11 NPC 三电平逆变器中点电位平衡实验波形Fig.11 Experimental waveforms in midpoint potential balance for NPC three-level inverter

4.2 NPC 三电平开关频率

图12 为条件下开关频率仿真波形时NPC 三电平MPFC 开关频率实验波形、给定转速300 r/min、给定负载4 N·m。图12（a）为不进行矢量筛选的传统MPFC 方法，开关频率为3.8 kHz；图12（b）为分扇区优化的MPFC 方法，开关频率为2 kHz。图13为相电流THD（total harmonic distortion）分析，可以看出传统MPFC 方案下相电流总谐波含量THD 为13.88%，而分扇区优化的MPFC 为15.24%，两种控制策略的电流THD 差别不大。结合图12 和图13可看出，两种方案的稳态性能基本一致。

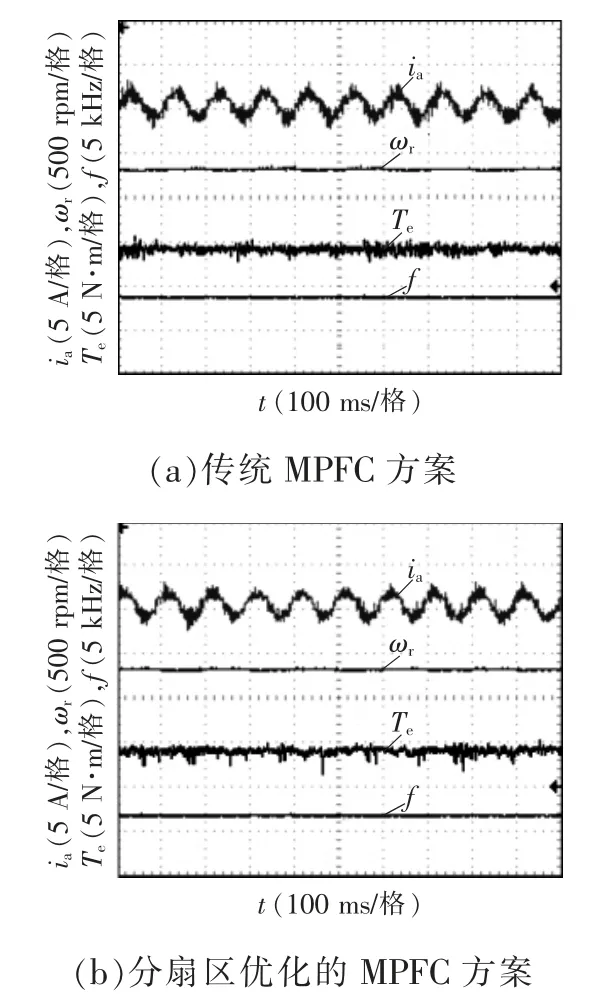
图12 NPC 三电平逆变器MPFC 开关频率实验波形Fig.12 Experimental waveforms of MPFC switching frequency for NPC three-level inverter

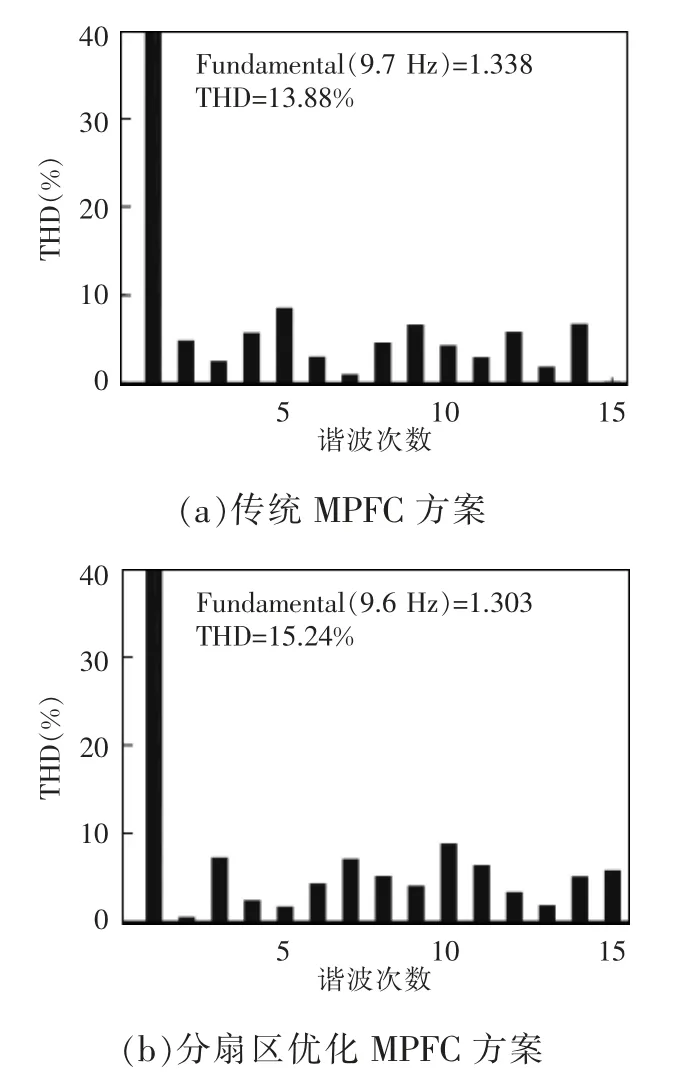
图13 相电流THD 分析Fig.13 THD analysis of phase current

图14 为分扇区优化的MPFC 动态波形。图14（a）为突变负载条件下的实验波形，给定转速300 r/min，负载由4 N·m 突变到6 N·m，转矩能在0.3 s内过渡到6 N·m，响应较快，转速在转矩变化过程中也能保持平稳。图14（b）为突变转速条件下的实验波形，给定负载4 N·m，转速由300 r/min 突变到500 r/min，转速能在0.2 s 内过渡到500 r/min 且基本无超调，在突变转速时转矩会出现较小的尖峰，但是能够随着转速的稳定而恢复平稳。根据动态实验波形可以看出，所提出的MPFC 策略具有良好的动态性能。

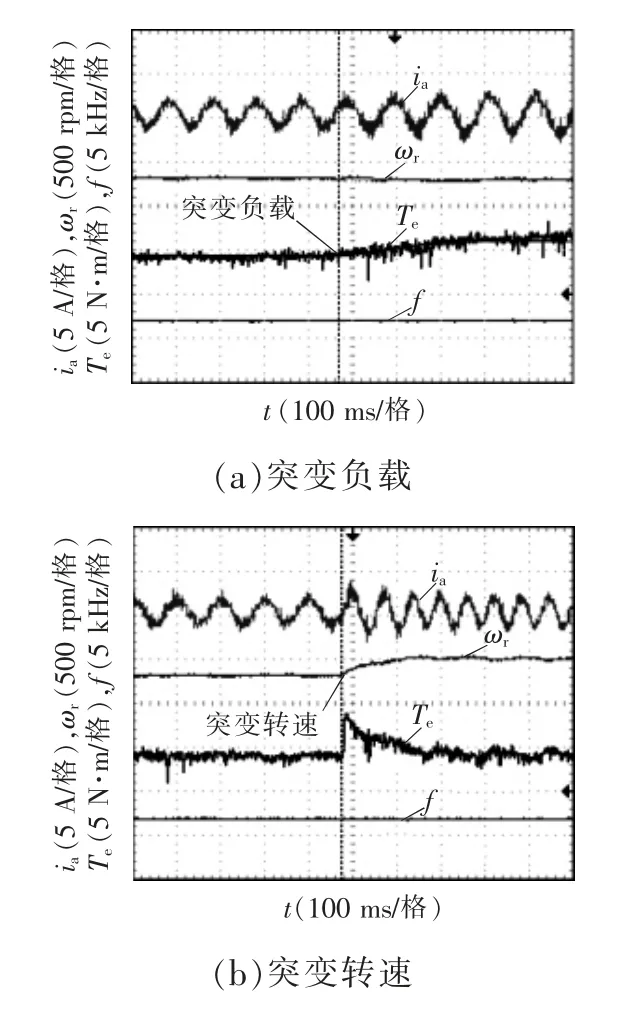
图14 分扇区优化的MPFC 动态波形Fig.14 Dynamic waveforms of MPFC for subregion optimization

5 结语

为降低开关频率，本文提出了一种计及开关频率分区优化的PMSM 三电平MPFC 策略。首先采用MPFC 消除传统MPTC 中的权重系数，根据上一时刻的开关状态，选择相邻扇区的矢量作为备选矢量，结合一个开关周期内只允许一相开关状态发生连续变化的限制条件，在有效降低开关频率的同时将备选矢量筛选到3～5 个。然后，通过正负冗余小矢量的合理替换实现中点电位平衡。最后，通过仿真与实验，验证了该控制方法的可行性。