基于模糊双线性模型的连续搅拌反应釜滑模控制

陈 珺,陈 汉

(江南大学 轻工过程与先进控制教育部重点实验室，江苏 无锡 214122)

0 引言

滑模控制是一种变结构控制，在非线性系统的分析中得到广泛应用，其优点显著：响应速度快，对于实际系统中存在的参数不确定性和外界的噪声干扰具有较强的鲁棒性，同时不需要对系统进行在线辨识。因此，被广泛应用于机器人控制、航空航天以及化工控制等领域[1-3]。然而滑模控制本质上是一类特殊的非线性控制，其非线性表现为控制的不连续性。由于现实中物理能量不可能无限大，这也限制了系统的加速度为有界值；此外，惯性存在于每一个系统中，这也导致滑模控制的切换量必然存在一定的滞后，正因如此，滑模控制的作用往往伴随幅值较大的抖振。系统性能受这种抖振的影响很大，如果没有妥善处理，整个系统的稳定性也难以保障，且在实际系统中控制器也难以实现。若要将滑模控制应用于非线性系统，可将与模糊逼近相结合，并采用基于模糊规则的模糊滑模控制方法，即可通过模糊化切换增益有效地抑制干扰项，并且消除抖振[4-6]。

双线性系统不同于一般的线性系统，有其特殊性，主要有两点表现：第一，它仅比线性系统多了状态变量和输出变量的乘积，即双线性项，形式上接近于线性系统，这种形式结构简易，因此便于控制；第二，对于一些特殊的非线性系统，其拥有比传统线性系统高得多的准确描述对象的能力。因此自问世之初，就引起了广泛关注并在许多领域得到了应用：核工程，信号和图像处理，通信，生物，生化，社会经济等[7-10]。近几十年来，许多学者研究了这类特殊系统的控制器设计和稳定性分析[11-13]。

T-S模糊模型可以以任意精度有效逼近实际被控对象，拥有良好的描述非线性系统的能力。鉴于双线性系统的特殊性，将T-S模糊模型和双线性系统相结合，模糊双线性模型应运而生。因其具有更好的描述非线性系统的能力，对T-S模糊双线性系统的研究引起了学者的广泛关注[14-16]。文献[14]研究了一类具有不确定性的连续模糊双线性系统容错控制问题，并结合了输出反馈和观测器以提升系统在故障状态的稳定性，文献[15]则讨论了不确定双线性混沌系统的鲁棒自适应同步问题，文献[16]对一类具有扰动的仿射双线性系统设计了鲁棒H∞模糊输出反馈控制器。

然而，在这些成果中，控制器的设计都是基于状态反馈或者输出反馈，形式较为单一，并且控制器的结构较为复杂，导致了较大的计算量。因此，一些学者研究了基于模糊双线性系统的滑模控制[17-18]。文献[17]考虑了带有模糊双线性噪声的滑模控制。文献[18]提出了一种将滑模控制应用于齐次双线性系统的控制方法，然而若将其应用于非齐次双线性系统，在有扰动情况下存在静差，精度难以保证。

基于上述原因，本文主要研究了一种可以应用于非齐次模糊双线性系统的模糊滑模控制方法。首先，根据系统结构构造积分滑模面，从而保证控制精度。当系统处于滑模面，为维持系统处于滑模面从而保证系统稳定性并满足性能指标，推导等效控制量。当系统状态游离于滑模面之外时，根据构造好的滑模面和趋近律，设计切换控制量，这样即可保证滑模控制的可达性。接着，根据滑模面和滑模面导数的范围对切换控制量进行模糊化处理，使控制量平滑化，便于实现。最后，以基于模糊双线性系统的连续搅拌反应釜的仿真实例验证了所提方法的有效性。

1 问题描述

考虑一类由T-S模糊双线性模型描述的非线性系统，其第i条规则如下：

Plant Rule i: IF ϑ1(t) isMi1and … and ϑp(t) isMip,

THEN

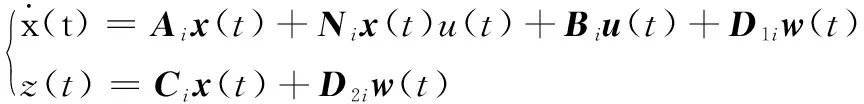
(1)

其中:x(t)∈Rn为状态向量，u(t)∈Rm为控制输入，w(t)∈Rl为平方可积的干扰输入向量，且满足|w(t)|≤d；ϑ1(t),...ϑp(t)为模糊规则的前件变量，Mij(j=1,2,...,p)为模糊集合，r为模糊规则推理数。Ai,Ni,Bi,D1i,Ci,D2i为具有适当维数的已知常数矩阵。

采用单点模糊化、乘积推理以及加权平均反模糊化的方法，可得模糊双线性系统的整体方程为:

(2)

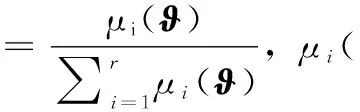
2 滑模控制器设计与稳定性证明

滑模控制方法可将系统状态引导到事先定义好的滑模面，并使其滑向平衡点。因此，滑模控制通常有切换控制us和等效控制ueq两个部分组成。切换控制是不连续的，并且只当系统不在滑模面时起作用，等效控制是连续的，目的是使系统在滑模面上运行。滑模控制器形式为:

u=us+ueq

(3)

接下来推导两个控制分量的具体结构与稳定性证明。

2.1 等效控制量

首先，定义如下积分滑模面:

(4)

传统滑模面为线性滑模面，即只有上式前一项，形式如下：

S(x)=Cx=0

该类滑模控制系统稳定性分析简单、便捷，参数设计相对容易，故线性滑模最早被提出，并应用广泛。但线性滑模在复杂非线性系统中应用的控制效果略显不足：对于带有扰动的复杂系统，会出现状态分量之间的误差成比例存在，此时滑模面函数也为0，这就造成控制精度难以保证。为此，采用式(4)的积分滑模面，积分项的引入，可显著提高控制精度。

为保证系统可以处于滑模面上运行，从而达到平衡点，需满足以下条件：当滑模面已经到达时，即S=0时，有：

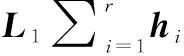
(5)

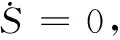
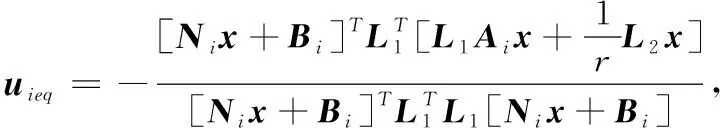
L1[Nix+Bi]≠0

(6)

结合并行分布补偿(PDC)算法，整体的等效控制量为:

(7)

为保证系统可在控制量(7)的作用下于滑模面上渐近稳定，给出如下定理：

定理1：若存在一个对称正定矩阵P，和L1，L2满足如下线性矩阵不等式(8)，则模糊双线性系统(2)在等效控制器(7)的作用下是渐近稳定的。

(8)

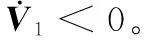
证明：取Lyapunov函数为V1=xTPx，P为正定对称矩阵。对V1的时间t进行求导得:

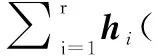
将等效控制量式(6)代入得:

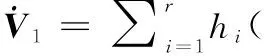
若满足如下条件:

(9)

证毕。

2.2 切换控制量

滑模面设计可以保证滑动模态运动品质，滑模切换控制律则可以保证系统有限时间可达性和提高趋近阶段的动态品质，使系统进入滑动模态。可达性指系统状态在有限时间内到达滑模面。滑模切换控制律可以根据趋近律设计，常见的趋近律有等速趋近律，指数趋近律，幂次趋近律，这里滑模切换控制器的设计是基于等速趋近律。

当满足如下条件，则滑模面的可达性可以保证：

(10)

为此，设计切换控制器形式为:

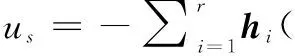
K≥L1D1id,L1(Nix+Bi)≠0

(11)

定理2：在控制器(7)和(11)的共同作用下，且满足L1[Nix(t)+Bi]≠0时，系统(2)将满足可达性。

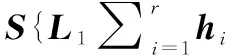
(12)

将式(3)代入式(12)中得：

D1iw]+L2x}=

证毕。

滑模控制的鲁棒性由切换控制得到保证，然而滑模控制的抖振也由切换控制中的符号项造成：当系统状态到达滑模面，由于惯性的影响，系统状态将穿过滑模面，此时在符号项的作用下，切换控制量符号瞬间取反，而增益不变，控制器输出变化剧烈，相应地，系统状态也会受其影响；当系统状态变化趋势已经处于滑模面附近时，状态量就会在控制器的作用下频繁穿越滑模面，这就是系统抖振。

为了消除抖振，应使切换控制在保证鲁棒性的同时尽量小，常用的方法有模糊推理，自适应滑模控制，高阶滑模等，这里使用的是曼达尼模糊推理。

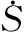
此时切换控制量形式为：

K≥L1D1id,L1(Nix+Bi)≠0

(13)

表模糊规则表

3 应用实例

连续搅拌反应釜(CSTR)是工业过程中最常用的一种化学反应器，它可以实现聚合反应，在石油、医药、试剂、食品以及合成材料等工业生产过程中占有相当重要的地位。一般来说，CSTR是在与最佳生产率相联系的某个平衡点上运行的，以追求最大的经济效益。从控制的角度来说，CSTR具有高度的非线性，特别是在具有外部干扰的情况下，因此难以通过常规方法取得令人满意的效果。为了验证所提方法的控制效果，以下将以CSTR系统为对象进行仿真研究。CSTR状态方程(14)如下[19]：

(14)

其中：x1(t)为反应釜中反应物的浓度，x2(t)为生成物的浓度，控制输入u(t)为稀释比例，w(t)=e-tsin(5t)为扰动。系统中动力参数选为k1=50 h-1，k2=100 h-1，k3=10 L/mol·h，CA0=10 mol/L。

假设x1(t)∈[0,10]，采用两个T-S模糊双线性模型来逼近CSTR系统(14)，即:

Rule 1: Ifx1(t) is about 0, THEN:

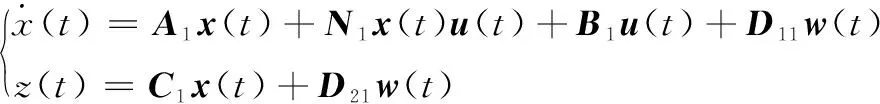
Rule 2: Ifx1(t) is about 10, THEN：

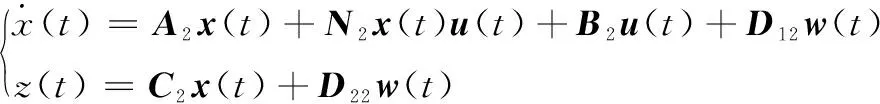
其中系统参数矩阵如下：

对应规则的模糊隶属度函数为：

h1(x1(t))=1-0.1x1(t)，h2(x1(t))=0.1x1(t)。

为便于比较，取系统(14)的一个平衡点：

xd(t)=[4.5 1.266]T，ud(t)=77.7272。

此时先将系统转化为基于误差的系统，形式如下：

Ni(e(t)+xd)u(t)+Biu(t)+D1iw(t)]

(15)

其中：e(t)=x(t)-xd(t)。

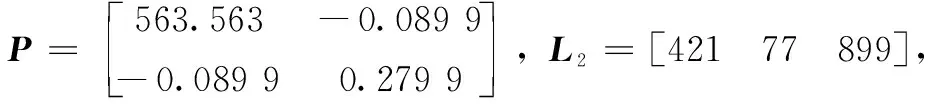
(16)

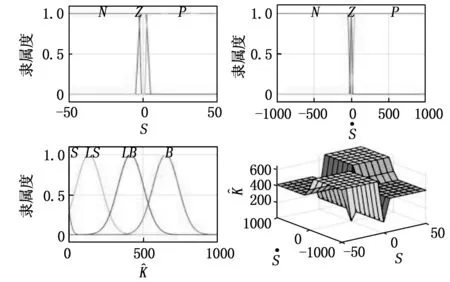
图的模糊规则隶属度函数

图2给出了该系统在初始条件x0(t)=[5.5 -1.8]T下的状态响应。由仿真结果可以看出，初始状态与平衡点差距较大，且伴有扰动。但在控制器(3)的作用下，系统状态响应经过短暂的过渡过程(大约0.1 s)后即可维持在给定的平衡点xd(t)=[4.5 1.266]T附近，因此所设计的控制器可以保证模糊双线性系统是渐近稳定的。

图3则是文献[18]的方法应用于连续搅拌反应釜的效果。对比文献[18]可知，文献[18]没有考虑扰动对系统的影响，且采用的滑模面为传统的线性滑模面。因此在有扰动的情况下，系统虽能维持稳定，但系统的状态和平衡点之间存在静差，且状态与控制量均持续抖动难以稳定；另外，由于切换增益无法随扰动改变，系统状态受扰动影响变化幅值明显大于本文所提方法。而本文在干扰存在的情况下仍能取得较快的响应时间和较好的过渡过程特性，并且控制精度也得到了保障。

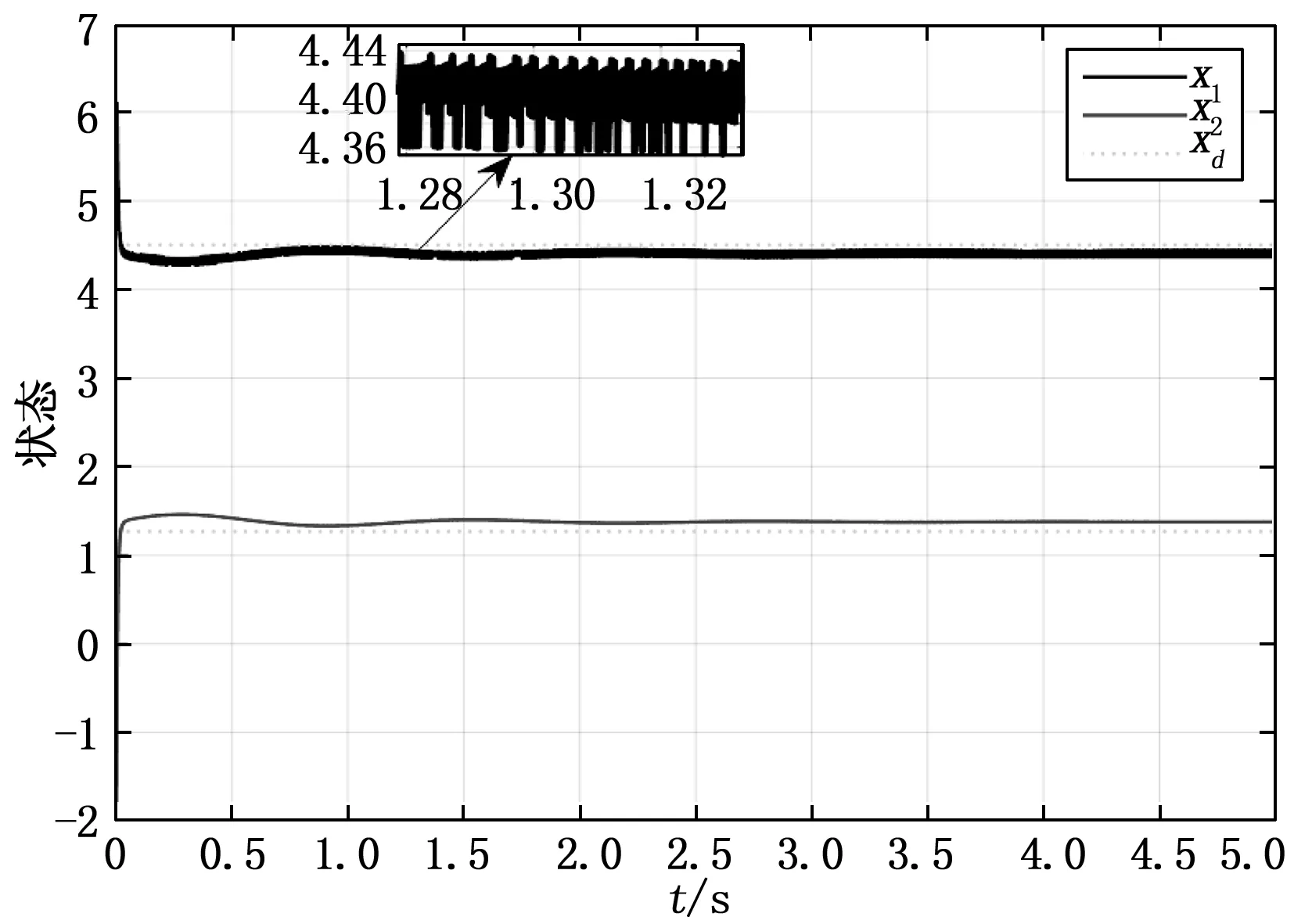
图3 文献[18]状态响应曲线

图4是本文提出的与状态响应相应的控制曲线。由图可知，控制量由大约58迅速升至平衡点77.727 2附近，为了克服扰动，存在一定的抖振，但在7条模糊规则的作用下，控制量逐渐平滑，实现了实际中的可操作性。当扰动消失时，控制量也稳定在平衡点。

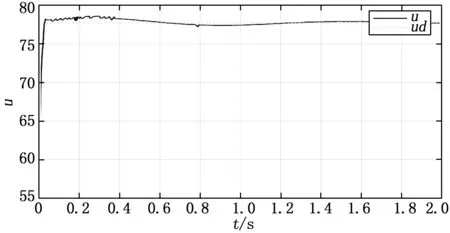
图4 系统的控制曲线

图5为滑模面函数对时间变化的曲线。由图可知滑模面一开始大约在42左右，这是因为初始状态与平衡点之间差距较大。但在滑模控制器的作用下迅速降至0左右，紧接着由于控制器抖振引起状态的抖振，滑模面函数也相应地小幅度起伏，但随即与控制量一起稳定下来。

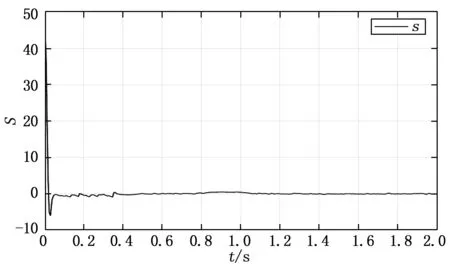
图5 滑模面随时间变化曲线

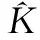
图随时间变化曲线

4 结束语

本文以连续CSTR为研究对象，引用T-S模糊双线性模型对其进行控制。通过对滑模控制中等效控制和切换控制的设计，给出了一个新的保证闭环模糊双线性系统全局渐近稳定的控制方法，从而使得系统具有较强的鲁棒性。模糊规则的引入解除了滑模控制的抖振现象，使得控制量连续化并且具有可实现性。最终通过仿真研究，验证了本文方法的有效性。

但是，本文的控制器设计也有所不足，控制器分母有一定的条件限制，滑模面的参数如果选取不当可能导致系统运行中发生奇异问题，从而引发系统不稳定和发散。未来，可就这一问题引入事件触发机制[20]，规避奇异问题的发生；此外，对于滑模面的选择，可以尝试性能更高的滑模面类型，如终端滑模面[21]，全局滑模面等，相信可以有更好的控制效果。