基于Gabor特征与加权协同表示的人脸识别算法

赵雪章，丁 犇，席运江

(1.佛山职业技术学院 电子信息学院，广东 佛山 528137;2.华南理工大学 经济管理学院， 广州 510641)

0 引言

随着计算机科技的发展，人脸识别技术在安防、教育、电子商务、金融等领域有着非常广泛应用，已经渗透到到人们的方方面面当中。人脸识别容易受到遮挡、光照、多姿态性、表情变化等因素的影响，这些不确定因素提高了人脸识别的难度。其中稀疏表示由于具有遮挡和腐蚀的干扰具有非常好的鲁棒性，以及对特征的选择不敏感等优点，被Wright[1]等人首次应用到人脸识别问题中，先直接使用所有训练祥本对测试样本进行线性表示，再通过最小重构误差对测试样本进行分类，特别是当测试样本有损坏或遮挡时，SRC方法依然有出色的分类性能，但当SRC线性组合的样本维数比较高时，时间复杂度大大増加。为解决这个问题，Hui和Ortiz等人[2-3]将SRC和线性嵌入思想相结合，提出基于线性近似的稀疏表示分类方法，在进行稀疏优化前，先利用线性回归对训练样本进行筛选，从而加快稀疏分解减少计算时间。另外的解决办法就是利用字典学习提高稀疏分解效率，利用字典学习可以获得信息量大但规模小的字典，字典原子个数远小于原始训练样本。2010年Zhang等人[4]提出具有鉴别性的D-KSVD算法，主要思想是在K-SVD算法的基础上引入分类误差项，该算法特点是学习到的字典具有鉴别能力；与此类似，Jiang等人[5]提出具有标签一致性约束的LC-KSVD算法，该算法是在K-SVD算法的基础上利用训练样本的标签信息，由于存在标签约束项使得同类训练样本的编码系数具有相似性，鉴别能力有较大的提高，但字典学习方法主要将重点集中在突出训练样本的编码系数或标签信息及字典原子的鉴别信息，忽略了训练样本的多样性，并且使用稀疏约束得到稀疏编码系数矩阵，计算效率不高。

所以协同表示分类被研究者提上日程，Zhang[6]等人于2011年提出基于2范数约束的协同表示分类(CRC)方法，这一方法表明SRC成功的根本原因不是稀疏约束，实际上是协同表示机制(CR)，此外还具备较为迅速的计算速度，更符合实际情况。尽管CRC方法对于CR机制在分类方面的高效性作出较为合理的解释，然而其几何解释存在较为显著的难点。因此Cai[7]等人在2016年提出了基于概率协同表示的分类方法(ProCRC)，从概率角度解释协同表示机制的分类原理。Lan等人[8]在此的基础上又提出通过提取训练样本的先验知识来提升分类性能的ProCRC方法(PKPCRC)。Yuan等人[9]提出协同竞争表示分类方法(CCRC)，利用不同类别的训练样本来竞争表示测试样本，通过竞争表示项针对表示、分类完成融合的过程，由此能够对分类功能进行具有针对性的优化。CRC方法却是以全局表示为基础的一种分类方式，通过全部训练样本完成线性组合的做成从而不断逼近测试样本，因此有很多和测试样本类别存在区别的训练样本，造成测试样本分类错误的可能性很强，此外在实际情况下因为训练样本的具体数目并非无限的，通过整体特征无法对光照变化、各种姿势表情等多种局部信息发生的变更进行良好的处理。

所以以局部特征为核心的分类算法被有关领域的研究人员予以高度重视，比如Gabor小波[8]这一性能优良的特征提取器，能够针对大脑皮层中存在的单细胞感受野对应的轮廓进行模拟，捕捉目标图像特定区域内的多位置多尺度多方向空间频率特性，从而能更好的克服光照、姿态和表情等全局干扰对识别效果的影响。除此之外，Akhtar等相关研究人员[9]通过大量研究结果指出，若针对协同表示系数对应的稀疏性进行提升，可以对分类功能的性能进行合理优化与改进。Yang等人[10]提出先对图像局部特征提取，然后通过学习编码得到具有Gabor特征的闭塞字典的方法提高了SRC识别准确率也减少了计算量；Hu等人[11]提出了判别式字典学习的稀疏表示识别算法，结合Fisher判别Gabor特征字典的学习得到字典原子对应类别标签的结构化字典，该典中特定类的子字典对相关的类的表示能力较好。

综上所述，此次研究提出以Gabor特征与加权协同表示为核心的人脸识别算法。在最开始的步骤中，必须针对人脸图像内所包含的各个尺度以及方向的Gabor特征完成提取的过程，初始特征样本字典实际上属于增广Gabor特征矩阵，并对其完成学习的过程，从而获得训练样本子字典，再在CRC方法中将样本对应的局部信息进行引入，从而进一步得到Gabor特征以及加权的协同表示分类方法[12-14]。

1 Gabor小波变换特征提取

Gabor 最早提出了将信号加窗后再进行傅里叶变换，当窗口函数取高斯函数时傅里叶变换就被称作为Gabor变换；Grbor变换可以从不同频率邻域及不同尺度方向上对图像进行处理，所以该方法通常在信号处理领域用来提取图像的纹理特征。在实际实践过程中一般采用Gabor变换作为线性滤波器在图像特征提取过程中对输入的图像样本进行小波变换，然后利用Gabor小波与图像进行卷积操作进而得到图像样本的Gabor特征。该特征在频率邻域和空间领域都具有良好的特性，能够较好地描述图像的空间频率、空间位置以及方向的局部特征信息。由于Gabor小波具备了这些特性，研究者经常利用它的多分辨特性对人脸图像进行局部特征的提取并增加系统的鲁棒性。

Daugman首次在二维空间结合小波理论进行Gabor变换，将一维Gabor滤波推广到二维构造出二维Gabor小波。

二维Gabor滤波器定义如下：

(1)

在实践中通过Gabor函数与图像I的卷积得到人脸图像I=(x,y)的人脸图像，对于任一像素点z0(x0,y0)，Gabor小波变换描述出点局部区域的图像特征，卷积过程定义为：

(2)

其中:*表示卷积，Ομ，ν(z0)表示在点z0(x0,y0)处的卷积值，通常如果对方向参数μ和尺度参数ν进行改变，就提取到不同方向下的多尺度局部特征，由各个不同像素点组成的集合，就构成了图像I=(x,y)的Gabor小波特征[16]。

公式(2)可以写为：

Ομ，ν(z0)=Mμ,ν(z0)·exp(iθμ，ν(z0))

(3)

Mμ,ν(z0)为幅值，θμ，ν(z0)为相位，幅值部分主要涵盖了图像局部能量的各种变化信息，所以图像特征对应的描述是经过变换过程的幅值。利用公式(2)完成卷积运算，基于像素点z0(x0,y0)进一步获取a×b个值，Gabor特征对应的维数较高，所以针对获取的幅值Mμ,ν(z0)首先需要针对单位方差利用均衡下采样同时完成归一化到零均值的过程，再进一步将其通过列进行连接，进一步组成Gabor小波特征向量[17-20]，表示为：

χ=[Gabor1(z0),Gabor2(z0),…，Gabora×b(z0)]T

(4)

χ是一个局部特征描述子。

2 加权协同表示方法

2.1 SRC方法

稀疏表示分类是指将测试图像表示为训练样本的线性组合，然后用l1或l2范数对保真度项进行编码，由Wright[1]等人提出的SRC方法作为稀疏理论的代表性成果，通过全部样本训练进一步共同构成字典原子，所对应的目标函数为公式(5)：

(5)

其中:λc为平衡参数，α所指代的是系数，在系数α被计算出来后，测试样本便能够通过分类被纳入最小残差值的训练样本的范围，可利用公式(6)进行分类：

(6)

其中:αi是第i类训练样本的表示系数。将SRC方法中目标函数的l1范数用l2范数代替，便是CRC方法[21-23]。CRC方法的函数公式为：

(7)

其中:β为表示系数，式(7)的解析解可用式(8)表示：

β=(XTX+λcI)-1XTy

(8)

在分类时各类训练样本的残差项和表示系数均含有鉴别信息[24-27]，都可以用来分类，分类规则为：

(9)

其中:βi是第i类训练样本的表示系数。

2.2 WCRC方法

在实践中，样本矩阵X中的列向量具有线性相关性，由此能够让矩阵XTX不断与奇异相接近，进一步造成矩阵内部对角线对应的值较高；此外所有样本及其邻近样本都有可能是同种类型，其表示系数具有较强的相似程度。Timofte等相关研究人员[9]以CRC方法为基础，进一步提出了WCRC方法[12-14]，其目标函数公式如下：

(10)

γ=(XTX+λwcWTW)-1XTy

(11)

根据公式(12)计算出WCRC方法的表示系数γ后，对测试样本y进行分类，分类规则为：

(12)

其中:γi是第i类训练样本的表示系数。

此次研究选择通过OMP算法[24]来完成对测试样本y所对应的稀疏系数α的计算过程。在这种情况下，增强加权所对应的表示系数如下：

(13)

ζ为增强系数。

假设L={l1,l2,…,lM}类样本，用m维向量表示每幅人脸图像特征，这里的向量已经过Gabor小波提取的特征向量。每个已标记类别的人脸样本数为n1,n2,…,nM，所以ci类别的ni幅人脸图像经Gabor提取后得到ni个m维的特征向量，那么标签矩阵则能够表示为Di=[di,1,di,2,…,di,n]∈Rm×n，测试样本表示为y∈Rm×1。

针对第i类样本Xi分布主要集中于标签矩阵Di的第i行，标签矩阵Di中所包含的非0元素数目为ni个。因此向量ϖ=Dζ所包含的第i个元素ϖi从本质上来看是i类训练样本Xi中所涵盖的所有表示系数ζi的和[25-27]。向量ϖ中包含的值能够作为所有训练样本中分类对应的得分值。所以测试样本y所对应的类别标签能够通过利用得分向量ϖ内存在的最大值而确定。

2.3 算法描述

此次研究的方法主要依据如下若干个步骤：

1) 根据式(1)～式(3)对每幅待识别的人脸图像进行Gabor小波变换，通过计算而获取的Gabor特征值先利用均衡下采样的方式并完成归一化至零均值的单位方差这一过程，再进一步以列为依据将其进行连接，进一步组成Gabor小波特征向量。

2) 通过OMP算法计算SRC方法的稀疏系数α[21]；

3) 利用公式(10)得出WCRC方法的表示系数γ；

4) 利用公式(12)得出增强系数ζ；

5) 计算WCRC方法测试样本y的分类向量ϖ=Dζ；

3 实验结果与分析

为了验证本文方法在人脸检测方面的性能，本文将在不同情况下作三组对比测试，实验1是不同数量测试样本训练识别，实验2是在Yale、Extended Yale B与AR数据库，实验3是人脸不同角度变化的测试。所有方法均在CPU为Inter Core i7-9700@4.9GHz，内存16G，操作系统为64位，Matlab2019a下进行。

3.1 不同数量测试样本训练及识别实验

本组实验是在LFW人脸数据库随机采集400个对象，由10种不同的代表一个人脸姿态的标签所组成，图像不对光照进行限制以验证实验对光照的鲁棒性。

在 LFW人脸数据库中分别选取数量为 50、100、200 和 400 个图像样本进行训练及测试，识别率见表1。

表1 不同数量训练样本的识别率

从表1中可以看出,对不同数量测试样本进行实验均可以达到较好的识别率及稳定性。

3.2 在Yale、Extended Yale B与AR数据库的实验

3.2.1 在Yale人脸数据库的实验

Yale人脸数据库由耶鲁大学著名的计算视觉与控制中心创建，数据库由15个受拍者每个人拍摄11张图片共165张人脸图像组成，所有人脸图像都以分辨率为100*100像素GIF格式存储的灰度图，这些人脸在拍摄时有较大的光照变化、姿态变化以及表情变化。

实验用的所有人脸图像被裁剪并采样为25*25像素，每个人随机选择8张人脸图像作为训练样本，其余的用作测试样本。在Yale人脸数据库中的实验都重复20次，SRC方法误差阈值η设为0.05。CRC方法与本文方法中平衡参数λc、λwc均为0.001，σ为0.4。

从表2中，支持向量机、稀疏表示分类、协同表示分类、融合表示分类与本文方法的识别率的比较可以看出，其他算法的识别率都高于支持向量机分类方法，说明稀疏表示分类在识别性能方面比支持向量机分类更优越；本文算法识别效率最优，主要利用训练样本的标签矩阵与测试样本的增强系数相乘得出分类分值，所以具有较高的分类效率，识别效率比支持向量机分类方法快10倍左右。

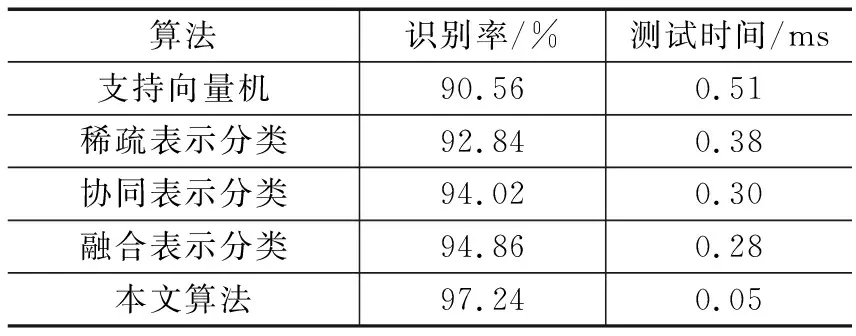
表2 在Yale中的识别率及测试时间

3.2.2 在Extended Yale B数据库实验

Extended Yale B人脸数据库也由耶鲁大学创建，库中包含38人共2 414张灰度格式的人脸图像，人脸图像存在大量的光照变化，大小为192*168像素。SRC方法误差阈值η设为0.05。CRC方法与本文方法中平衡参数λc、λwc均为0.001，σ为0.4。所有方法在Extended Yale B人脸数据库中都单独运行10次。并计算出平均识别率和单个测试样本进行识别的平均测试时间。

此次实验在AR数据库内选择一个子集，涵盖的图像中男性受试者人数为50名，女性受试者人数也为50名。

表3是通过Gabor小波变换对样本集进行PCA降维后特征维数d=300时的结果，可以得到本文算法取得了最高的识别率，而且是SRC分类效率的4倍，原因是本文算法在降低特征维数的时保留原空间的最有效信息，从而保持较好的识别性能，并且降低了计算复杂度，具有较高的分类效率。

表3 在Extended Yale B中的识别率及测试时间

3.2.3 在AR人脸数据库的实验

AR人脸数据库于1998年由西班牙巴塞罗纳计算机视觉中心建立，累计人数为126人，具有超过四千张的彩色图像。拍摄此类图像需要经历两个阶段，分别是将环境中的所有表情变化进行搜集、对若干种光照条件以及遮挡是否存在变化进行检测，人脸图像的尺寸等于165*120像素，σ等于0.5。在AR数据库中一个子集进行测试，包括50名男、女共2 600张图像，每张图像随机投影到向量空间中。每人随机选10张人脸图像为训练样本，剩余为测试样本。SRC方法的误差阈值为0.05，CRC方法的正则平衡参数与本文方法相同λc、λwc均为0.001。所有方法在AR人脸数据库中都单独运行10次。并计算出平均识别率和单个测试样本进行识别的平均测试时间。

从表4中可以看出，提出的方法可以获得更高的面部识别率，此外，在鲁棒性方面也较强，比经典的SRC算法错误识别率大约降低58%，而且识别速度得到显著提高，说明本文算法表示思路的合理性。

表4 在AR中的识别率及测试时间

3.3 人脸不同姿态变化的实验

FERET人脸数据库由美国国防部商级研究计划局创建，包含1万多张人脸灰度图像，这些人脸图像在各种光照条件、多种脸部角度及各种面部表情的情景下拍摄。主要选择FERET人脸数据库的一个常用姿态库子集对头部不同角度变化问题进行测试，该数据集由200个受拍者共1 400张人脸图像组成，每人7张人脸图像，3幅为正面图像，4幅为各种角度图像，分别标记为“ba、bj、bk、be、bf、bd、bg”。实验中每张人脸图像都被采样到40*40像素。我们进行5组不同姿态角度的测试，在实验1(姿态角度0°)，每一类图像中前1-2的图像作为训练样本，每人人脸图像第3个的为测试样本；剩余的4组实验中，前1～3的图像为训练样本，然后分别用bg(-20°)、bf(-15°)、be(+15°)、bd(+25°)作为测试样本，取得人脸不同角度下的识别结果。在实验中通过Gabor小波变换对对样本集进行PCA降维后特征维数d=300。参数设置与前面相同。

图1给出了不同算法在人脸不同角度下的识别率，从图中可以得到，当人脸角度偏转不大的情况下(0°±15°)，支持向量机算法对角度变化很敏感；随着偏转角度的增大，当角度变化较大时(达到±25°)，所有的算法的识别率都明显下降，但本文的算法仍然高于其他算法。本文算法Gabor特征描述图像局部信息的优点，显著地提高了识别率，本文算法相比其他算法更好的克服了人脸角度变化的影响。实验结果表明本文算法在姿态变化不大的情况下显著的提高了识别效果，在实际中具有一定的实践价值。

图1 FERET人脸数据库算法结果

本文所选的算法在FERET人脸数据库测试中都有随着训练样本和测试样本数量的增加而识别率下降的问题出现，这有可能与选择训练样本方式有关，更为合理的应当是采用随机选取方法，后期将在FERET人脸数据库的训练样本加入随机策略方式进行验证。而且本文提出的算法需要确定3个参数，分别是权重参数σ和正则项平衡参数λ及SRC方法误差阈值η。经过研究本文方法对两个参数不敏感，但当误差阈值为0.05和正则项平衡参数λ=0.001时，文本方法的识别率达到最佳数据。

4 结束语

本文提出了一种基于Gabor特征与加权协同表示的人脸识别算法，先提取人脸图像多尺度多方向的Gabor特征，将增广Gabor特征矩阵作为初始特征样本字典，对该特征字典进行学习，形成训练样本子字典，与协同表示分类相比，由于考虑样本的局部信息和表示系数的稀疏性，这样使得协同表示分类中较为“稠密”的表示系数的稀疏性增强，系数的表示能力得到提升，降低重构误差，使得以本文算法为核心的人脸图像识别算法在Yale人脸数据库、Extended Yale B和AR人脸数据库的实验中都取得最高识别率和较短的分类时间，具有一定的实践价值。但在现实应用中，人脸存在姿态变化、光亮度变化及遮挡等因素，使训练及测试样本同时被噪声影响，未来会针对训练样本由于受到污损或遮挡的情况进行研究，提高抗噪能力。