一种结合灰狼算法的粒子群优化算法

李 真，王 帆，王冉珺

(1.中国科学院 光电技术研究所,成都 610209； 2.中国科学院大学,北京 100049；3.中国科学院 空间光电精密测量技术重点实验室,成都 610209；4.中国科学院 西安光学精密机械研究所,西安 710000；5.中国科学院 空间精密测量技术重点实验室,西安 710000)

0 引言

群体智能算法[1]如蚁群算法[2]、鲨鱼算法[3]、蜂群算法[4-5]、遗传算法[6-8]、粒子群算法[9-11]近几年逐渐成为学者们研究的焦点，由于粒子群算法(PSO,particle swarm optimization)易于实现且复杂度相对较小，已广泛应用于多个不同的工程领域[12-13]，但粒子群算法存在一个天然缺陷，就是其在搜索的过程当中，易陷入局部最优，即最终通过粒子群算法找到的值与全局最优值有一定的差距，针对此缺点许多学者提出了许多改进策略。文献[14]将提出将遗传算法与粒子群算法结合使算法能够快速收敛，文献[15]将粒子群算法的位置更新公式进行改进，增强其搜索能力，文献[16]将混沌策略加入粒子群算法当中，改善了其易陷入局部最优的缺点。文献[17]对粒子群算法的参数进行调整，平衡全局和局部的搜索能力.

本文同样针对粒子群算法易陷入局部最优的缺点，对粒子群算法进行改进，由此提出了一种改进的粒子群优化算法(PSO_GWO)，主要改进策略包括最差粒子进行进化策略和对最优粒子进行扰动的策略，以及结合灰狼算法搜索能力强[18]的优点，将灰狼算法的优势引入粒子群算法中，并且选取了9个常用的标准测试函数进行测试，从收敛速度和寻优精度两个方面进行了对比，仿真结果表明所提算法有效。

1 粒子群算法

粒子群算法(PSO)是1995年Kennedy[11]提出的通过仿照鸟群寻找食物的过程的一种进化算法，其基本思想是将粒子看作没有体积和质量的个体，每个粒子都有速度和位置两个特征，每个粒子在每次迭代过程中朝着粒子群全局最优和自身历史最优趋近，不断进化寻找更优值。粒子群算法迭代更新公式如下：

(1)

(2)

2 粒子群优化策略

由于粒子群算法有易陷入局部最优的缺点，其陷入局部最优的原因主要有两点：第一点是由于粒子群算法在迭代后期会发生聚集造成种群多样性下降；第二点是在算法迭代更新公式中只考虑了个体经验和最优粒子的引导作用，同样会导致算法出现多样性下降和早熟收敛的问题。所以，本文为提高粒子群算法的搜索能力，提出了改进粒子群算法(PSO_GWO)，分别提出了最差改进策略、最优粒子扰动策略，并结合灰狼算法对迭代更新公式进行改进，其中最差粒子改进策略是为了提高粒子群算法在搜索过程中的多样性，而最优粒子扰动策略则是为了防止算法后期发生聚集导致搜索能力下降，灰狼算法的引进是为了改进现有粒子群算更新公式中所存在的缺点。

2.1 最差粒子改进策略

由于粒子群算法是一种模仿自然界中鸟群觅食的过程提出的一种智能优化算法，受自然界中“优胜劣汰”生存法则的启发，对粒子群算法中的进行优化，即在每次迭代过程中对适应度最差的粒子进行进化，其主要目的是为了增加粒子群的多样性增强算法的搜索能力，如果进化后的粒子的适应度优于未进化时的适应度，则将进化后的粒子替换掉未进化的粒子，如果进化后的粒子的适应度比未进化时的适应度差，则保留未进化时的粒子。对最差适应度的粒子进化策略具体如下：

x_worst(t)=argmax(fit(x1(t)),fit(x2(t))…

fit(xN(t)))

(3)

Eworst(t)=xi(t)+rand(xj(t)+xk(t))

(i≠j≠k∈1,…,N)

(4)

x_worst(t)=

(5)

式中，x_worst(t)表示第t次迭代时，N个粒子中最差适应度的粒子，其中N表示粒子群的数量为N。式(4)中Eworst(t)表示进化后的粒子的位置，其中i、j、k为在粒子种群中随机选择的3个互不相同的粒子。如式(5)所示，若进化后的粒子的适应度优于未进化的粒子的适应度，则替换掉进化前的粒子。若进化后的粒子的适应度比未进化的粒子的适应度差，则保留原有粒子。

2.2 最优粒子扰动策略

在算法迭代后期，由于粒子群发生聚集导致粒子群的搜索能力下降，从而使得粒子群算法极易陷入局部最优。粒子群算法的全局最优位置gbest(t)在整个粒子群算法寻优过程中对种群有很强的引导作用，全局最优位置会引导所有粒子朝着全局最优位置方向进行，所以可以根据粒子群的聚集程度，对全局最优位置进行扰动，从而增大粒子群的全局搜索能力。

(6)

ri=|xi-avg_x|

(7)

(8)

式中，avg_x(j)表示粒子群中所有粒子的中心位置的第j维，i表示第i个粒子。式(7)中ri表示第i个粒子与粒子群中心位置的距离，式(8)表示所有粒子到中心位置的平均距离。若avg_r较大说明粒子群较为分散，即说明粒子群还具有很强的多样性，此时只需要对全局最优位置进行较小的扰动，即增强粒子群的局部搜索能力。若avg_r较小说明粒子群较为密集，此时粒子群的多样下降，甚至粒子群可能已经陷入局部最优，此时需要对全局最优位置进行较大的扰动，使得全局最优位置引导粒子群跳出局部最优，即增强粒子群全局搜索能力。对全局最优位置的扰动策略如式(9)，使用指数函数对全局最优粒子进行扰动，avg_r较小时，对应的指数函数值较大，即产生的扰动较大。反之，对应的指数函数值较小，即产生的扰动较小。

Nbest(t)=sign(rand-0.5)exp(-avg_r)

gbest(t)+gbest(t)

观察图4～图8发现，钢筋连接件荷载-变形曲线的模拟结果略大于试验结果，偏心试件模拟结果和试验结果吻合较好。最大荷载值的相对误差：试件H400-20为25%，试件H500-16为5.2%，其余试件为3%左右，偏移试件基本都为1%左右。通过ABAQUS建立模型得到的模拟结果整体较好。表3所示为有限元分析结果与试验结果的对比。

(9)

(10)

式中，若扰动后的粒子的适应值优于扰动前的粒子，则将扰动前的粒子替换为扰动后的粒子；反之，扰动前的粒子将不进行替换。

2.3 灰狼包围优化策略

最差粒子进化策略提高了粒子群算法的多样性，最优粒子进化策略帮助算法在迭代后期跳出局部最优，针对粒子群算法迭代更新公式中只考虑了个体经验和最优粒子的引导作用，导致算法出现多样性下降和早熟收敛的问题。本文结合灰狼算法对其更新公式进行改进，主要原因是灰狼算法在迭代更新时，采用精英群体引导策略，即选择群体中最优的3个精英个体进行引导更新，而不再是粒子群算法中最优的一个个体进行引导。而且灰狼算法采用的是包围式引导策略，即在搜索对过程中，其他粒子会包围式的向精英群体进行趋近。所以将粒子群算法与狼群算法进行结合可以进一步提高算法的搜索能力。

灰狼算法中最重要的搜索策略的包围式搜索策略，其数学模型如下。

X(t+1)=Xp(t)-A×D

(11)

D=|C×Xp(t)-X(t)|

(12)

其中：t为迭代次数，Xp(t)是猎物的位置向量，X(t)是灰狼的位置向量。其包围示意图如图1所示。

图1 灰狼算法包围策略示意图

C=2r1

(13)

(14)

其中:r1、r2为[0,1]之间的随机数，a为控制参数在[0,2]内随着迭代次数线性递减,递减公式如式(15)：

(15)

由上述对灰狼算法的介绍中可知，灰狼算法在进行引导时，其采用精英群体对种群进行引导，即选择最优的3个精英个体对种群进行引导。灰狼种群中最优的3个精英个体分别是最优解α、次优解β以及第三最优解，3个精英个体均会根据(11)、(12)对整个种群进行包围式的引导，其引导策略具体公式如下：

Dα=|C1×Xα(t)-X(t)|

(16)

Dβ=|C1×Xβ(t)-X(t)|

(17)

Dδ=|C1×Xδ(t)-X(t)|

(18)

其中：式(16)～(18)为群体中灰狼个体分别距离前3个最优解α、β、δ的距离，式(19)～(21)为灰狼种群分别向3个精英个体移动的方向，式(22)为结合3个精英个体引导后，灰狼算法的更新公式：

X1(t)=Xα(t)-A1×Dα

(19)

X2(t)=Xβ(t)-A2×Dβ

(20)

X3(t)=Xδ(t)-A3×Dδ

(21)

(22)

为引入灰狼算法包围式搜索的全局搜索能力强的优点，将粒子群算法的更新公式改为式(23),即在粒子群算法更新公式中添加灰狼算法的包围式更新策略：

(23)

通过式(23)可以看出，在粒子群算法的位置更新过程中，保留了粒子群算法原本的个体经验和最优粒子的引导，并且引入了灰狼算法更新策略X(t),其不仅包含了灰狼算法的精英群体的引导策略还包含了灰狼算法的包围式搜索策略。通过引入灰狼算法，可以弥补粒子群算法在迭代更新公式中存在的不足。

3 仿真分析

为验证算法的有效性，采用表1中的9个测试函数进行测试，这9个测试函数表示不同的参数空间并且拥有不同的特性，可以充分考察算法的寻优能力，函数表达式和函数的搜索范围以及9个函数的全局最优值如表1所示，其中f1～f3、f6～f9为单峰函数,表示只有一个最小值；f4～f5为多峰函数，表示有多个局部最小值，将优化算法在不同函数上进行寻优，测试算法性能。

表1 9个不同的测试函数函数

3.1 算法寻优精度对比分析

将PSO、GWO、GAPSO、PSOd以及本文提出的改进粒子群算法(PSO_GWO)分别对测试函数寻优，每种算法的种群规模均为N=20，算法的迭代次数均为Tmax=1 000，对每种算法重复运行20次，对20次的结果求均值(mean)和方差(std)进行对比，最终对5种不同算法的性能进行了排名(rank)，5种算法的寻优精度对比以及最终的结果排名如表2所示。

由表2可知，将本文提出的改进粒子群算法(PSO_GWO)与其他4种算法做对比时，函数f1、f2、f4、f5、f6、f8均可找到全局最优值0，而标准粒子群(PSO)和改进位置更新公式的粒子群算法(PSO_d)在对这6个函数进行寻优时，均未找到全局最优值0，并且最终找到的值与全局最优值0差距较大。对于f7函数，对比其他4种算法，PSO_GWO的寻优精度与GAPSO的寻优精度相同，但是比较其他3种算法其寻优精度提高了1～16个数量级。对f3函数进行寻优时，PSO_GWO的寻优精度比较其他4种算法寻优精度提高了1～4个数量级。对f9函数进行寻优时，PSO_GWO的寻优精度比较其他4种算法寻优精度提高了1～4个数量级，综上所述，PSO_GWO在对不同测试函数上进行寻优时，只有在f7函数上进行寻优时，寻优结果与GAPSO,在其余函数上进行寻优时的寻优结果均是优于其他4种算法的，所以在对5种算法进行综合评价时，PSO_GWO的综合排名是处于第1位的，即PSO_GWO在寻优精度上是优于其余4种算法的。

表2 不同测试函数寻优精度对比

3.2 算法收敛性能对比分析

图2为不同算法对不同函数寻优时的收敛曲线，可以看出对函数f1、f4、f5、f6、f7、f8进行寻优时，PSO_GWO算法在前期的收敛速度较慢，在后期明显加快，其中在对f1函数的寻优过程中，PSO_GWO算法在迭代90次时，达到其他4种算法迭代200次的寻优精度。在对f4进行寻优时，其前期的收敛速度略差于GAPSO，但其在80次迭代时，可达到其余4种算法在200次的寻优精度。在对f5函数的寻优过程中，PSO_GWO算法在迭代120次时，达到其他4种算法迭代200次的寻优精度。在对f6函数的寻优过程中，PSO_GWO算法在迭代80次时，达到其他4种算法迭代200次的寻优精度。在对f7函数的寻优过程中，PSO_GWO算法在迭代83次时，达到其他4种算法迭代200次的寻优精度。在对f8函数的寻优过程中，PSO_GWO算法在迭代70次时，达到其他4种算法迭代200次的寻优精度。在对f9函数的寻优过程中，PSO_GWO算法在迭代初期开始寻优速度就是优于其他4种算法的，其迭代30次时，达到其他4种算法迭代200次的寻优精度。但在对f2、f3进行寻优时,PSO_GWO的寻优速度虽优于PSO、GWO、PSOd三种算法但略差于GAPSO。综上所述，PSO_GWO除了在对函数f2、f3进行寻优时的速度略差于GAPSO，在对其他函数上进行寻优时，寻优速度均是优于其他算法的。

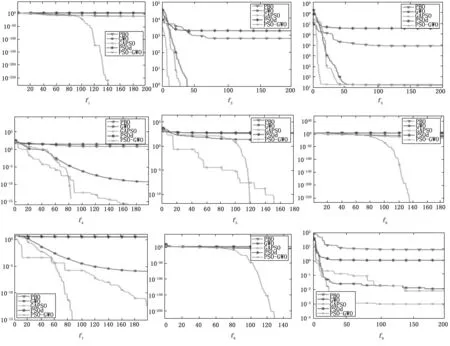
图2 各种算法在不同函数的寻优曲线

4 结束语

本文提出了一种结合灰狼算法的粒子群优化算法(PSO_GWO)，主要思想是对粒子群最差粒子进行进化，提高粒子群的多样性以及对最优粒子进行扰动使粒子群跳出局部最优，此外还结合灰狼算法的精英群体包围式搜索策略增强粒子群算法的全局搜索能力，最后将改进完的粒子群算法(PSO_GWO)与标准粒子群算法(PSO)、灰狼算法(GWO)、遗传粒子群算法(GAPSO)、改进位置更新公式的粒子群算法(PSOd)在9个标准测试函数上进行寻优精度和收敛性能的对比。在寻优精度上，PSO_GWO在对9个函数进行寻优时，对其中6个函数均找到了全局最优值0，对其他3个函数进行寻优时，即使未找到理论最优值0，但比较其他4种算法依旧提高了1～16个数量级。在收敛性能上，除f2、f3函数外，在对其他7个函数进行寻优时，在前200次迭代均能达到其余算法的收敛精度。由此可以看出，PSO_GWO在寻优精度和收敛性能上均是优于其他4种算法的。本文将所提算法主要用于自抗扰控制器[19-20]的参数自整定中，其主要原因是控制系统处于不同的环境当中时，控制对象的模型会发生改变，由此会造成参数不适用的现象，为了使控制系统的参数在不同的环境下均有良好的控制效果，本文将粒子群算法(PSO)和改进粒子群算法(PSO_GWO)均用于自抗扰控制器的参数自整定中去，结果表明PSO_GWO的整定的参数的控制效果更优。