一种割草机无刷电机高频注入启动策略研究
葛海康,潘海鹏
(浙江理工大学 机械与自动控制学院,杭州 310018)
0 引言
手推式割草机主要应用于绿化草坪的养护,能够极大程度地节省人力资源。在手推式割草机电机的启动过程中,需要做到快速、平稳、无反转启动,并要避免产生较大的抖振[1-2]。现阶段,手推式割草机主要使用表贴式的无感无刷电机作为动力源,常用的启动方法主要有:三段式启动、电感法、短时检测脉冲启动法、高频注入启动等[3-4]。
无感无刷电机在启动中可分为初始位置定位和加速两个阶段,常规三段式启动方法在转子初始位置定位阶段会造成转子反转,因此对割草机电机并不适用[5]。在此基础上可以通过电感法和短时脉冲法进行转子定位,解决启动中转子反转的问题,但定位精度较低[6]。初始位置定位后进入电机的加速阶段,可通过升频升压的方法进行开环加速[7],但割草机电机可变负载的特性会造成启动中失步的情况。文献[7]改进了外同步加速阶段,通过注入不同电压矢量,对其产生的对应电流与电流阈值的对比作为换向条件,使电机处于闭环加速状态,提升了转速提升的平稳性。但电流阈值设置不精确,会导致换向精度低,加速阶段不平稳的问题。
高频注入法的优点在于转子初始位置定位精度高,不会出现转子反转,而且加速阶段处于双闭环中,提高了电机启动中转速的平稳性[8]。割草机电机常用表贴式无感无刷电机,具有很小的凸极率,只能采用脉振高频注入的方式,利用电机的饱和凸极性响应来得到转子的位置信息[9]。传统高频注入方法多采用弦波注入,信号处理过程复杂,与之相比方波信号无需对高频响应信号进行较多的滤波处理,在开关频率较低时,能够获得更好的调制效果[10]。使用脉振方波高频注入时,通常使用带通滤波器提取高频响应电流信号,并对带通滤波器的带来相移进行补偿[11-12],来提高转子位置和转速判断的准确性。文献[13]在提出了一种利用高频方波注入的条件下,高频响应电流和基频电流的关系,使用软件算法取代滤波器的使用,解决了滤波器带来的相移影响位置估计精度的问题,但在电机转速较高时,由于采样点的选择带来的误差,难以保证转子位置估计的精确度。此外,在电机首次启动时需要对旋转坐标轴系d轴的极性进行判别[14],文献[15]使用传统的注入正负脉冲的方法,分别在转子位置角正向和反向各注入恒定电压,利用磁路的饱和效应确定d轴的极性,但实验证明此方法用时较多,不利于割草机电机的快速启动。
通过以上分析,可采用脉振方波高频注入的方式实现割草机电机的启动,论文对高频响应电流采用低速和高速两个阶段分离选取采样点的策略,确保电机全转速运行中转子位置估计的准确性,提高割草机电机在启动的平稳性,并使用改进的正负脉冲注入的方法确定d轴的极性。
1 表贴式无刷直流电机模型
使用脉振方波高频注入法估计转子的位置时,需要在估计的转子同步旋转坐标系中的直轴注入高频方波信号,由于高频感抗远大于纯电阻,纯电阻项可忽略不计。而在低速时,高频模型中的交直轴耦合项和反电动势部分占比很小。在同步旋转坐标系dq轴系下电压方程为:
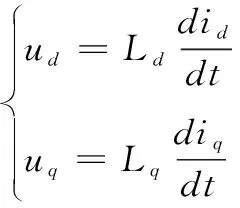
(1)
式中,下标d、q分别为直轴和交轴,u为电压量;L为电感量;i为电流量。将其写为矩阵形式:
(2)
式中,p为微分算子。
2 脉振方波高频电压注入
脉振方波高频电压注入的方法,要求在转子估计同步旋转坐标系dhqh轴系中的dh轴,注入高频的方波电压信号。转子同步旋转坐标系为dq轴系,两相静止坐标系为αβ轴系,电机三相绕组中A相绕组与α轴重合,各坐标系之间关系如图1所示。

图1 各坐标系之间的关系
d轴和A相绕组轴线的夹角为θ,dh轴和A相绕组轴线的夹角为θh,dh和d轴夹角为Δθ,α轴和A相绕组轴线重合,其中夹角关系如式(3)所示:
Δθ=θ-θh
(3)
目前提取高频响应电流的方式可分别在dq轴系和αβ轴系实现,可通过检测在αβ轴系下的高频电流响应,来对转子的位置进行估计。如图1所示,从dhqh轴系到dq轴系可通过旋转Δθ得到,如式(4)所示:
(4)
同理,dq轴系到αβ轴系的变换如式(5)所示:
(5)
使用高频方波电压注入时,方波电压的信号可表示为:
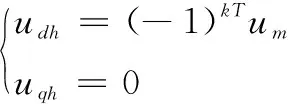
(6)
其中:k=0,1,2,3,…;T为注入方波信号的周期;um为方波电压的幅值。
将式(2)代入式(4)中,可得出在dq轴系下的高频电流响应,如式(7)所示:
(7)
由式(5)和式(7)可得出在αβ轴系下的高频电流响应,如式(8)所示。
(8)
将式(3)和式(6)代入式(8),用平均电感L=(Ld+Lq)/2和半差电感ΔL=(Lq-Ld)/2表示Ld、Lq,并进行化简可以得到αβ轴系下的脉冲响应为:
(9)
对于表贴式无刷直流电机,近似认为Ld≈Lq,假定在一个采样周期内电流呈线性变化,式(9)可变换为:
(10)
由式(10)可知,在αβ轴系下的高频电流响应包含转子的位置信息,可以对iα轴和iβ轴的高频电流响应进行信号处理作为转子位置估计的输入信号,以此获得转子的位置和转速。从式(10)可知,当半差电感ΔL≈0时,仍可以从高频电流响应中得出转子的估计角度,验证了此方法对表贴式直流无刷电机具有适用性。
3 割草机电机的启动策略
3.1 初始角度估计
割草机电机在启动过程中可分为转子初始定位阶段和加速阶段。在初始定位时,使用脉振方波高频注入算法可以避免转子的反转。在估计转子坐标轴注入高频方波信号,此时转子处于静止阶段,采样得到的iα和iβ只包含高频电流响应,通过式(10)可知,其包含转子的位置信息。使用的正反切的方法,将iαh和iβh直接引入位置计算,通过状态追踪可得到对应的转速和位置信息,计算过程如式(11)所示:
(11)
但割草机电机在启动过程中,实际的电流信号中包含各种外界干扰,将电流信号直接引入正反切函数的除法运算会使得外界干扰被放大,致使估计位置和转速产生较大的误差。为降低对噪声的敏感程度,可将高频响应电流作叉乘运算,以得到位置误差Δθ,再通过锁相环进行位置和转速估算,其估算过程如图2所示。
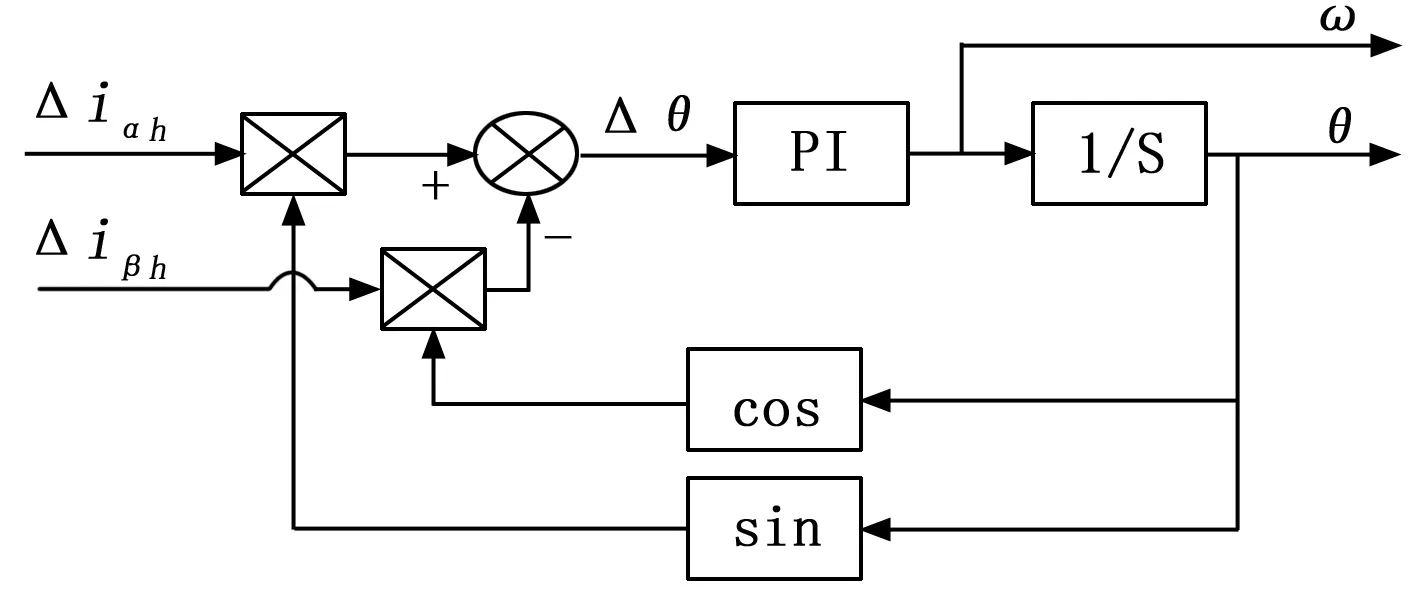
图2 位置和转速估算
3.2 转子的极性判断
通过锁相环的方法可得到静止状态和转动状态下转子的位置和转速,通过式(10)可知,Δθ有一个稳定平衡点Δθ=0,和一个不稳定平衡点Δθ=π,动态下Δθ总会收敛到稳定平衡点。但在静止状态下,在初次位置估计得到初始角度θ后,需要对d轴的极性进行判定,以确定电机转子的实际位置[16-17]。注入电压的幅值和频率将会影响电机启动性能,当注入电压幅值或频率过小会增大极性判断的难度[14],反之则会导致转子的抖动。
在估计角度θh注入高频电压,通过图2所示的位置估计方法可得到转子初始角度θ,此时割草机电机转子的实际位置有θ和θ+π两种情况。在角度收敛到θ过程中,在dq坐标系下进行分析,可由式(7)得到:
(12)
由式(12)可知,在Δθ≈0时,Δidh会随着L的增大而减小,随着L的减小而增大。在得到转子初始角度θ的过程中,记录下注入角度为θh时的高频电压得到的电流响应幅值,并做平均值滤波处理,记为idh1。记录完成后,再注入相同幅值和频率的,角度为θh+π高频电压向量,并记录电流幅值,记为idh2。假定实际位置θm=θ,即θ为d轴的极性为正方向,此时需要对|θ-θh|的大小分情况讨论。
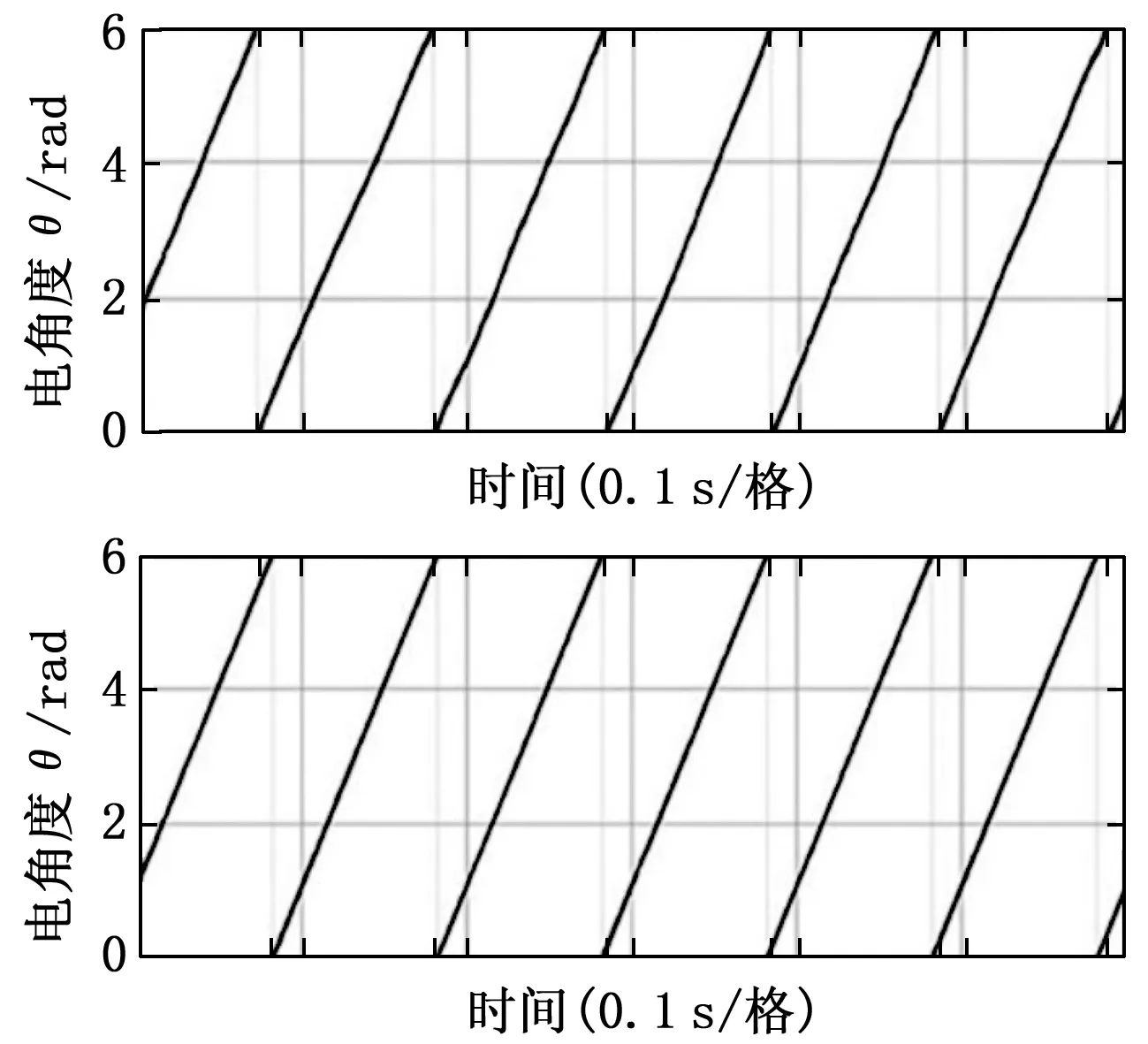
以估计角度θh注入时为例,在估计坐标轴dh注入如式(6)所示的方波电压,通过式(4)可转换为,在转子初始角度θ注入幅值为udhcos(|θ-θh|)的电压向量,当cos(|θ-θh|)>0时,相当于在初始角度θ的正方向进行电压注入,反之则相当于在θ+π注入电压。当|θ-θh|<π/2时,若此时idh1>idh2则说明时假设正确,θ为电机转子的实际位置;若此时idh1 (13) (14) 当|θ-θh|>π/2,idh1和idh2的大小和转子实际位置的关系则相反,若idh1>idh2则说明时假设错误,电机转子的实际位置为θ+π;若idh1 加速阶段工作在电流环和速度环中,此时iα和iβ不仅包含高频电流分量还包括基波电流分量。其中高频电流分量包含割草机电机转子的位置信息,因此需要解调出高频电流分量,将此信息作为位置估计的输入,最终估算出转子的实际位置。通常使用低通滤波器提取基波分量,通过带通滤波器提取高频分量,但滤波器的使用会导致相移的产生,使位置和转速的估计出现误差,致使割草机电机在启动过程中出现抖振的情况,甚至启动失败[18]。为解决此问题,可利用基波响应电流和高频响应电流的关系,进行解耦运算。 通过3.1节所述方法得到转子的位置信息,需要采样得到Δiαh和Δiβh,再将作叉乘运算得出的Δθ代入锁相环中,通过比例积分控制器将Δθ调节至零,估计位置则会最终收敛到转子的实际位置。在得到Δiαh和Δiβh的过程中,以磁场定向控制常见的七段式控制为例,其示意图如图3所示。在一个周期内,开关器件的状态发生改变,器件的续流作用会使iα和iβ产生非线性的变化,若将这种非线性变化作如式(10)所示的近似处理,会对位置和转速的计算带来误差。 图3 采样点分析 在割草机电机转速提升的过程中,当转速较低时,零矢量作用时间较长,在零矢量作用的中点Tzero,此时开关器件无开关状态变化,可降低续流作用对采样电流的影响[19-21]。当转速较高时,零矢量的作用时间变短,有效矢量时间变长,开关器件的续流作用在零矢量作用期间内变得明显,因此可选择在有效矢量的中点Topen进行采样,此时开关器件状态不发生变化,可以减少开关器件产生的不利因素。后续实验通过割草机电机在3 000 r/min时,选择不同采样点得到电流信号估计转子的位置信息,验证了两个采样点得到的位置信息的差异。以Topen时刻的电流采样过程为例进行分析,当高频电压的信号的注入信号为开关频率的一半时,两者具有如图4所示的关系,Ts为开关频率的载波信号周期,Tin为高频的注入信号周期,将Tin延迟Ts半个载波周期。 图4 高频解耦信号分析 以iα为例,在t-1时刻采样得到的iα包含的基波电流分量和高频电流分量关系如式(15)所示,在t时刻三者具有如式(16)所示的关系: iα(t-1)=iαf(t-1)-iαh (15) iαt=iαft+iαh (16) 其中:iαf为基波电流分量;iαh为高频电流分量;iα(t-1)和iαt分别为t-1时刻和t时刻采样得到的α轴的电流值。在允许一个采样周期误差的情况下,t时刻的基波分量可表示为: (17) 同理,t时刻的高频电流分量可表示为: (18) 割草机电机启动过程中负载变化主要体现在对基波电流的影响上,在位置估算过程中,利用式(18)所示的原理,可消除基波电流的变化对位置估算的影响。上述的电流信号的处理方法避免了使用带通滤波器带来的时间延迟,降低了位置估计的误差,而且在不使用低通滤波器的情况下可以得到基波电流,由式(17)可以看出,以此方法得到高频电流分量存在一个采样周期的延迟,但在实际的闭环系统中,这一延迟是客观存在的,后续的实验验证了此处理方法的有效性。通过同样的方法可得到iβ的高频电流分量和基波电流分量,在得到t-1时刻和t时刻的iαh和iβh后,相减得到Δiαh和Δiβh,应用于图3所示的锁相环中,计算得出转子的实际估算位置和转速,用于加速阶段的速度控制,基波电流分量应用于内环电流的控制,其具体控制过程如图5所示。 图5 整体控制框图 为验证上述分析和方法的有效性,使用一台500W割草机用直流无刷电机进行实验。电机参数:极对数为9,额定转速3 500 r/min,母线电压36 V,定子电阻R=0.6 Ω,定子电感LS=0.75 mH,转动惯量为280 g/cm2,永磁体磁链为0.127 Wb。使用STM32F302R8T6作为控制芯片搭建电路,通过示波器采集D/A转换接口得到电机的位置和速度的波形,并通过网线连接PC端和示波器实时监视。实验配置如图6所示。 图6 实验配置 系统母线电压为36 V,载波频率为16 kHz,注入电压幅值取3.6 V,频率是载波频率的一半为8 kHz。在电机静止状态下,得到注入方波信号后的相电流响应,图7为A相电流响应曲线。注入电压的频率会对高频响应电流产生较大影响,注入频率越低,高频响应电流的幅值越大,逆变器的基波电流输出的畸变率就越高[13]。在开关频率较低时,要尽可能提高注入频率,降低逆变器的非线性特性带来的影响。 图7 高频电流响应 将位置估算信号通过D/A转换输出到示波器可得到转子角度波形,图8为启动阶段前0.08 s的角度数据。分别取|θ-θh|<π/2和|θ-θh|>π/2两种情况下,电机转子实际位置判断情况。当判断出d轴极性与假设相同时,如图8右两图所示,角度收敛到转子的初始位置保持不变;当两者相反时,如图8右两图所示,转子初始位置会迅速调整到θ+π,可以看出在约0.06 s左右,初始角度收敛到实际位置。 图8 初始角度估计 设置斜坡的加速直线,在0.1 s时进入加速阶段,以在0.5 s时速度提升至2 000 r/min,并保持不变,速度观测波形如图9所示,电机转速达到追踪效果。 图9 转速变化 在闭环加速阶段,电机的转速和位置观测值由图4所示位置估算器给出,图10为转子角度反馈波形,在加速初始阶段,速度和角度的存在波动,但在0.3 s后速度观测值趋近于设定值,角度观测波形更为稳定;在0.5 s时,角度周期约为0.03 s。 图10 加速阶段角度估计 割草机电机工作时,电机转速在3 000 r/min以上[2],以最终转速到达3 500 r/min。当电机转速为3 000 r/min,此时占空比较大,仍在Tzero采样,开关管的噪声将对采样电流产生较大影响,图11上图为电机转速为3 000 r/min时,对在Tzero采样得到的相电流,进行处理和估算得到的角度观测波形。在此情况下,电机的转子角度的估计值存在明显波动,造成割草机电机在启动提速过程产生抖振情况的发生,图11下图为在Topen采样相电流,进行处理和估算后得到的角度观测波形。结果证明在占空比较高时,在载波周期中点采样能使割草机电机在启动过程中更加平稳。 图11 不同采样点的估计角度 论文分析了割草机电机在启动中存在的问题,在脉振高频方波注入法的基础上,提出了一种用于转子初始位置判断的转子极性判别方法,提高了电机启动速度;并提出了一种转子加速阶段的分阶段的电流采样策略,改善了割草机电机启动阶段角度估计的准确度。实验证明,在转子初始位置判定阶段,能够快速、准确地判断d轴极性;在加速阶段,低占空比时能够实现割草机电机在启动过程的平稳提速,二段加速时,使用优化的信号处理方法提高了角度估计位置的精确度。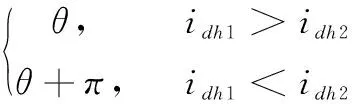

3.3 高频电流的解耦



4 实验分析





5 结束语

