新定义题的解题策略:逻辑加直观,动静卡边界

【摘 要】 文章以2022年北京市中考数学卷压轴题为例,分析新定义题的价值和试题结构.通过对该压轴题的剖析和解答,总结出解答新定义题的一般解题策略:逻辑推理突出几何直观,动静结合卡准边界位置.
【关键词】 新定义题;解题策略;几何直观;边界位置
新定义题是中考试卷中的一类特殊题型,一般是指在某种情境下借助新符号定义新运算新法则,或给某种数学变换关系定义新概念等.要求考生现场学习,解答新问题.考查考生的阅读、理解和迁移能力.
而北京市中考数学卷从2012年到2022年的11道新定义题则不同于通常意义下的新定义题,试题的立意、结构、综合性和试题功能等均有很大不同.这类新定义题不仅考查数学抽象、逻辑推理、直观想象、数学运算等重要的数学学科能力,还考查包括学习能力、探究能力等更普适性、对学生未来的学习都非常重要的能力[1].
下面以2022年北京市中考数学卷压轴题第28题为例,谈谈该类试题的一般解题策略.
1 新定义题及其结构
2022年北京市中考数学卷延续了用新定义题压轴的试卷结构,试题如下:
在平面直角坐标系xOy中,已知点M(a,b),N.
对于点P给出如下定义:将点P向右(a≥0)或向左(a<0)平移a个单位长度,再向上(b≥0)或向下(b<0)平移b个单位长度,得到点P′,点P′关于点N的对称点为Q,称点Q为点P的“对应点”.
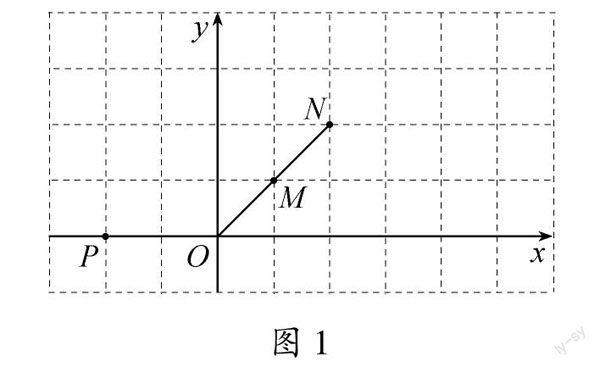
(1)如图1,点M(1,1),点N在线段OM的延长线上.若点P(-2,0),点Q为点P的“对应点”.
①在图中画出点Q;
②连接PQ,交线段ON于点T.求证:NT=12OM;
(2)⊙O的半径为1,M是⊙O上一点,点N在线段OM上,且ON=t(12 可以看出,这类新定义题属于代数与几何高度综合题,试题包括题干(新概念的定义部分)和问题(理解和运用部分).试题的命制均在平面直角坐标系中进行,问题部分一般包括起始问题、台阶问题和综合问题,具体结构如下表1所示. 2 来自学生的反馈 新定义题备受命题者的青睐,学生对新定义题的态度如何呢?6月18日,笔者对我校毕业班学生进行了“关于新定义题我是这么看”的问卷调查. 第1题:你对新定义题(第28题)的态度( ). A.非常喜欢 B.喜欢 C.谈不到喜欢也不讨厌D.不喜欢E.非常讨厌 调查数据(图2)表明,31%以上的学生表示不喜欢,甚至近10%的学生明确表示非常讨厌这类题型,有超过79%的学生对新定义题没有好感.第6道题的调查数据佐证了这个结果. 第6题:对于北京中考卷中的新定义题型,你认为( ). A.继续保留B.无所谓C.应该废弃 调查发现,近30%的学生认为应该废弃新定义题,如图3.进一步调查,支持“应该废弃”的前三条理由是:给我造成很大的心理压力;浪费时间,也得不了几分;不知道考啥知识.而这些理由的背后是学生们的一个共识——新定义题“一题一法,题无定法”. 因此,研究新定义题的一般解题策略有非常强的现实意义——想学生之所急,研学生之所需. 3 一般解题策略 美国数学家M·克莱因在《古今数学思想(第四册)》中论述:“数学的直观,就是对概念、证明的直接把握.”德国数学家希尔伯特在《直观几何》一书中认为:“图形可以帮助我们发现、描述所研究的问题,可以帮助我们寻求解决问题的思路,可以帮助我们理解、记忆得到的结构.” 以上强调几何直观的学术观点可以指导我们学习数学研究数学,也可以指导我们解答新定义问题:逻辑推理突出几何直观,动静结合卡准边界位置. 3.1 用笔读题三遍 解答新定义题的第一关是数学阅读,这也是一道心理关.在有限的时间内和紧张的氛围下要求考生阅读三四百字的试题,“不仅包括对数学文字语言、符号语言、图表语言的理解、记忆、认知等过程,还包括对材料的逻辑结构进行分析、综合、归纳、推理、猜想等一系列思维过程,(数学阅读)是区别于一般阅读的较为复杂的智力活动.”[2]其难度可见一斑. 常言道,书读百遍其义自见.因此,我们建议学生平时养成“用笔读题三遍”的习惯. 第一遍,通读题干,初步了解题目涉及的几何元素和大致的几何变换过程.比如,点M,N,点P平移得到P′,点P′关于点N对称得到点Q,等. 第二遍,研读新定义,用笔圈点关键信息,弄清几何元素如何变换,怎样建立什么关系,新概念的含义和记号等.比如,点P平移得P′,点P在哪儿,和日常所学的平移含义相同吗?平移的方向和大小受谁制约?点P′关于点N对称得到点Q,点N在哪儿?谁和谁是“对应点”?此题“对应点”有什么具体含义?等等.需要考生反复阅读,这个过程最好画画草图,如图4,建立几何直观,使新定义可视化. 第三遍,跳读题干,厘清几何变换关系,明确几何变换过程,整体上明晰新定义的几何模型.比如,给定点P,根据点M平移得点P′,点P′关于给定的点N对称得点Q,称点Q为点P的“对应点”.此时,可以提炼出新定义的关系图(如图5). 3.2 试做起始问题 起始问题是对新概念的具体辨析和直接应用,引导考生把抽象的新概念和变换关系具体操作一遍,促进对新定义的理解,建立几何直观模型. 问题(1)以如图和坐标的形式给出点M(1,1)和P(-2,0),至于点N的坐标是不是(2,2),所给图形虽然有网格衬托,但并没有说明点N在格点(当然,格点也需要定义)上,所以,考生可以认为N(2,2),這样更方便画出P′(-1,1),Q(5,3),完成起始问题(1)①,如图6. 事实上,起始问题的命制目的应该不是描点画图,而是有尺规作图的味道,当然,此题无需尺规作图.(近几年的北京中考卷都有一道尺规作图题(第20题),而今年换成了证明三角形内角和定理(第20题).命题人是不是想借此弥补尺规作图呢?) 根据题意,PP′∥OM,且PP′=OM,P′,N,Q三点共线,且P′N=NQ.题中蕴含平行四边形PP′MO和线段P′Q的中点N.这为解答台阶问题做好了准备. 3.3 解答台阶问题 台阶问题是对起始问题的横向拓展或纵向拓展,也是为探究最后的综合问题做好铺垫,起到登堂入室的台阶作用.因此,解答台阶问题不能为了解题而解答,而应该是在解答的过程中思考并提炼一些方法和结论,总结基本活动经验,进而在综合问题中迁移运用. 台阶问题(1)②在起始问题①的基础上继续构图和探讨,如图7,根据题意又构造出△PP′Q及其一条中位线NT. 如何证明PP′∥OM呢?可以根据平移的性质,几何直观得到PP′∥OM;更严谨的推理则过点P′,M作x轴的垂线,构造分别以PP′和OM为斜边、以1为直角边长度的等腰直角三角形,由两三角形全等得同位角∠P′PO=∠MOx,判定PP′∥OM,且PP′=OM,进而得PP′∥ON. 由对称变换知N是线段P′Q的中点,根据平行线分线段成比例的基本事实知T是线段PQ的中点,即线段NT是△PP′Q的一条中位线,所以NT=12PP′=12OM. 根据对台阶问题的解答,我们更加清楚了点P只要不在直线OM上,“对应点”模型中N,T分别是线段P′Q,PQ的中点,包括NT=12OM等都没有变化.还有,我们进一步明确了寻找“对应点”Q的过程,M是主动点,P′是从动点,而“对应点”Q又是受点N影响的从动点. 整个解答过程,分析的基本方法是按照题意有序构造几何关系,探究的基本依据是平移变换、对称变换和平行线分线段成比例.我们带着这些基本活动经验解答综合问题. 3.4 攻克综合问题 综合问题的命制通常是对台阶问题的一般化,让一些元素动起来(点M在⊙O上动,点N在线段OM上动,点P的位置也不确定了),增加了很多“不确定”因素. 此时,需要考生调整一下疲劳的身心,伸伸懒腰,做个深呼吸,静下心来再次集中精力对综合问题“用笔读题三遍”,明确哪些几何元素或关系变化了,哪些没有变化,能否和台阶问题关联上,等等.好在综合问题一般都是要求直接写出答案,需要严谨的数学推理,但不需要规范的步骤书写,此时,动静结合卡边界就至关重要. 第一步,明确“不确定”,分析特殊情况,试着画画图. 为方便画图,减少不必要的不确定因素的干扰,我们不妨把没有限制的元素取特殊但又不失一般性的位置,比如点P(-3,0),此时可以考虑点N的两个特殊位置. 因为ON=t(12 第二步,动静结合,卡准边界,确定最值位置. 我们已经通过有序的推理和构造把“对应点”模型以及相关关系直观化了.连接PQ交半径OM于点S,当点M在⊙O上运动时,从动点P′和Q分别在⊙P,⊙R上运动,在动态分析中卡准点Q与点P和点R共线时的边界状态,此时PQ取得最值(最值对应的位置往往都是唯一的),所以(PQ)max-(PQ)min=PR+RQ-(PR-RQ)=2RQ.或者也可以考虑△PRQ三边的关系和边界位置得到不等式PR-RQ≤PQ≤PR+RQ,即(PQ)max-(PQ)min=2RQ. 第三步,利用好台阶问题,借步作答,准确运算. 如何求⊙R(实线圆)的半径呢?如果考生掌握梯形中位线的知识,求解非常快捷:RQ+PP′=2ON,RQ=2t-1.不用梯形中位线,两次利用三角形中位线推导也不复杂:在△QPP′中,NS=12PP′=12,则OS=ON-NS=t-12.在△PRQ中,RQ=2OS=2t-1,所以(PQ)max-(PQ)min=2RQ=4t-2. 至此,针对于考试算是解答完毕.但对于该题还有很多问题可以继续思考,包括作为解答题如何严谨、规范的书写解题步骤,除了上述PP′∥OM的严格证明,还有点P′和点Q的轨迹为什么是圆?点P的位置一般化时对⊙R有何影響?又为什么对试题的结果没有影响?还有什么解答思路?该题蕴含的思想方法能否一般化,等等. 4 结束语 东北师大史宁中教授多次强调:在大多数情况下,数学的结果是通过观察最先猜出来的,而不是“证”出来的,数学学科中,对于结果的预测和对于原因的探究,起步阶段依赖的都是直观.新颁发的《义务教育数学课程标准(2022年版)》认为“几何直观有助于把握问题的本质,明晰思维的路径”,要养成“运用图表描述和分析问题的意识与习惯”.《高中数学课程标准(2017年版2020年修订)》则要求学生能够在各种情境(熟悉的、关联的、综合的)通过几何直观提出问题、分析问题、解决问题,并能直观表达,体会几何直观的作用和意义.可见,几何直观是学好数学的关键能力,当然也是解答数学问题(尤其是新定义问题)的首要意识. 最后,我们用流程图的形式直观表达解答新定义问题的一般策略,如图9. 解答新定义题的总策略是紧扣新概念,联系老知识,运用常规方法,在逻辑推理下突出几何直观(逻辑加直观),在可变几何元素的动态变化中寻找边界位置(动静卡边界). 具体操作:(1)用笔读题三遍,画出新定义(几何元素间的变化过程和建立的关系); (2)比葫芦画瓢,回答起始问题.回顾新定义,直观化理解新概念; (3)重视台阶问题,总结新定义背景下的思想方法和新结论,搭建脚手架; (4)现学现卖,动静结合,逐层拆解分析,运用新方法新结论攻克综合问题. 我们常说“无圆不几何”,对于北京市中考卷新定义题则有“无圆不新定义”的解题经验,最后的综合问题一般落脚点都是圆或圆弧.这也是上述调查中最后一题学生回答使用频率最高的词语. 参考文献 [1]顿继安.问题变式视角下数学新定义型综合题的设问路径——以2020年北京市中高考数学题为例[J].基础教育课程,2020(08):101-107. [2]任子朝,陈昂,赵轩.加强数学阅读能力考查,展现逻辑思维功底[J].数学通报,2018(06):8-13. [3]王亮亮.重现命制过程剖析思路变化——以2012年北京市压轴题为例[J].数学通报,2014(03):48-51. [4]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022. [5]中华人民共和国教育部.高中数学课程标准(2017年版2020年修订)[M].北京:人民教育出版社,2020. 作者简介 史嘉(1980—),男,安徽亳州人,中学高级教师;获第七届全国高中数学青年教师优秀课展示活动一等奖,主持并完成省级教育科学规划课题两项;发表文章多篇. 中学数学杂志(初中版)2022年4期
