挖掘内涵 变式创新

【摘 要】 文章首先分析了含60°角的菱形的图形结构及试题特征;再以含60°角的菱形为载体，通过多角度挖掘图形内涵，融入模型变式深化，打破思维定势拓展创新等途径，编制出一系列问题;最后针对不同层次的班级，选择问题构建一题一课专题教学，培养学生探究和解决数学问题的思维能力和创新意识.

【关键词】 挖掘内涵;变式创新;菱形;编制试题;一题一课;专题教学

1 提出问题

在人教版八年级下册“平行四边形”章节的教学中，常常会遇到与含60°角的菱形有关的问题.究其原因，是含60°角的菱形中包含着两个等边三角形，两个含120°角的等腰三角形，以及四个含30°角的直角三角形，具备多种特殊的边和角的关系，为试题的编制提供了良好素材.

当在此基本图形中添加含特殊角度60°的图形元素（特别的，如等边三角形）后，在线段的夹角、角度的和差、图形的全等中会形成更为多样的组合形式，也就产生了以此为背景的融入手拉手模型、夹半角模型、一线三等角模型而编制的问题.例如图1是菱形中典型的夹半角模型问题，其中∠ABC=60°，∠PAE=60°，题目蕴含丰富结论，解题的关键是利用图形中特殊的边角关系构造全等三角形.

本文尝试以含60°角的菱形为载体，从多个角度挖掘图形内涵，编制一系列变式题，问题由浅入深，体现考点交汇，隐藏显性要素，淡化模型记忆.进而针对不同层次的班级，选择相应问题构建一题一课专题教学.

2 试题编制2.1 挖掘内涵，体现技能

从最初的含60°角的菱形开始，在左侧嵌入等边三角形中的常见考题，形成如下问题.

问题1 如图2，在菱形ABCD中，∠ABC=60°，连接AC，点H，F分别在线段AC，BC上，CH=BF，AF与BH相交于点P，则线段AF与BH有何数量关系，∠APH为多少度.

分析 根据图形中的已有条件直接证明△ABF≌△BCH，应用全等的性质及角度的转换即可解决问题.事实上，只要保持CH=BF，就有∠APH的度数为60°，适当添加线段可构成一个与菱形共A点的等边△APE.

将全等图形从一个等边三角形移至两个等边三角形中，形成如下问题.

问题2 如图3，在菱形ABCD中，∠ABC=60°，连接AC，点E，F分别在线段BC，AC上，BE=AF，DF的延长线交AE于点P，求∠APD的度数.

分析 本题全等的证明与问题1类似，但所求结论更具隐蔽性，需要对角度进行合理的转换.由△DAF≌△ABE可得∠ADP=∠BAE，所以∠APD=180°-（∠PAD+∠ADP）=180°-∠BAD=60°.适当添加线段亦可构成一个与菱形共D点的等边△DPG.

在菱形右侧的等边三角形中融入旋转模型，隐藏AC，增加对线段数量关系的考查，得到如下问题.

问题3 如图4，在菱形ABCD中，∠ABC=60°，△DPG是等边三角形，C，P，G三点共线，连接AG，则∠AGP为多少度，线段GA，GC，GD之间有何数量关系.

分析 本题实质上是共D点的手拉手模型，但设计图形时未连接AC，旨在淡化固有的模型记忆.由∠ADC=∠GDP=60°，得∠ADG=∠CDP，所以△ADG≌△CDP，∠AGD=∠CPD=120°，所以∠AGP=120°-∠PGD=60°.因为GA=PC，GD=GP，所以GA+GD=PC+GP=GC.2.2 变式深化，凸显本质

将旋转模型移至菱形顶点A处，即以A为顶点构造等边△APE，同时隐藏AC，随着△APE旋转到不同位置，其与菱形可形成不同的组合方式.下面以点P在射线BD上运动的三种位置为例，依次设计出如下三个问题.

问题4 如图5，在菱形ABCD中，∠ABC=60°，点P是线段BD上的一动点，以AP为边向右侧作等边△APE，连接CE.当点E在菱形ABCD内部时，线段BP与CE有何数量关系，BP与CE的夹角为多少度.

分析 连接AC，△ABC和△APE构成手拉手模型，同问题3，有△ABP≌△ACE，所以BP=CE，∠ACE=∠ABP=30°.延长CE交BD于点H，因为AC⊥BD，所以BP与CE的夹角∠BHC为60°.事实上，还可证明出△ABP≌△DCE.

问题5 如图6，在菱形ABCD中，∠ABC=60°，点P是线段BD上的一动点，以AP为边向右侧作等边△APE，连接CE.当点E在菱形ABCD外部时，求证：PD+CE=3AD.

分析 类比问题4，连接AC交BD于点O，由∠BAC=∠PAE=60°，得∠BAP=∠CAE，所以△ABP≌△ACE，BP=CE，所以PD+CE=BD.所求结论中设置系数3，目的是引导学生联想到菱形中的含30°角的Rt△ADO，或含120°角的等腰△ABD，从而得出BD=3AD，所以PD+CE=3AD.

此外，由∠BAD=120°，∠ABD=30°可联想到过點D作AD的垂线交BA的延长线于点H，如图7，构造出含120°角的等腰△BDH和含30°角的Rt△ADH，也能得出BD=DH=3AD.

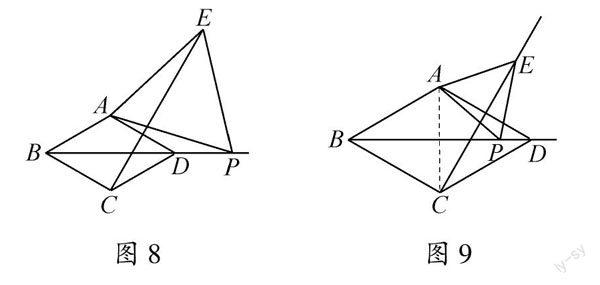
问题6 如图8，在菱形ABCD中，∠ABC=60°，点P是BD延长线上的一动点，以AP为边作等边△APE（A，P，E逆时针排列），连接CE.则线段AD，PD，CE之间有何数量关系.

分析 类比问题5，连接AC，证明△ABP≌△ACE，BP=CE，所以有CE-PD=3AD.

问题4，5，6逐层递进，隐蔽全等要素，打破模型化的几何图形设计方式，从两线段的相等关系到多线段的和差倍分关系，强调分析问题、解决问题的探究能力和思维品质.

在点P运动的过程中，两个三角形始终保持全等关系，故图形中的另一动点E的运动路径存在规律，可设计如下问题.

问题7 在菱形ABCD中，∠ABC=60°，点P是射线BD上的一动点，以AP为边作等边△APE（A，P，E逆时针排列），连接CE.当点P在射线BD上运动的过程中，点E的运动路径是什么？

分析 本题融入了对线型伴随轨迹问题的考查，延续了问题4，5，6的思路，达到无缝衔接.如图9，因为△ABP≌△ACE，∠ACE=∠ABD=30°，CE=BP，所以点E的运动路径为∠ACD的角平分线CE，运动路径长与点P相同.

将点P脱离BD，等边△APE旋转到菱形外侧时，可形成更具一般性的旋转问题.

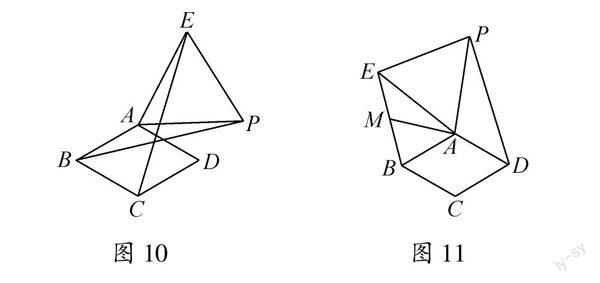
问题8 如图10，在菱形ABCD中，∠ABC=60°，点P是菱形外的一动点，以AP为边在菱形外侧作等边△APE（A，P，E逆时针排列），连接BP，CE交于点O.求BP与CE的夹角度数.

分析 类比问题6，连接AC，有△ABP≌△ACE，∠AEC=∠APB，所以∠EOP=∠EAP=60°，BP与CE的夹角度数为60°.

2.3 拓展提升，创新思维

为打破思维定势，变换图形位置，寻找新的图形构造方式设计问题.如图11，尝试改为连接BE，DP，得到两个全新的△BAE和△APD，其中∠EAB+∠PAD=180°，即“对应角”由前面的旋转角相等变为了互补关系.在此图形背景下可形成如下问题.

问题9 如图11，在菱形ABCD中，∠ABC=60°，点P是菱形外的一动点，以AP为边在菱形外侧作等边△APE（A，P，E逆时针排列），连接BE，DP，点M为BE的中点.求证：DP=2AM.

分析 本题不是简单套用前述方法连接AC证明全等.而是要根据所求结论联想到倍长AM，或将PD截半，或构造中位线等方式，如图12，图13，图14，图15，将其转换为证明两线段相等的问题，从而构造出一组新的全等三角形解题，凸显创新思维.

以图12为例，延长AM使得MN=AM，连接BN，可证明四边形ABNE为平行四边形，所以BN∥AE，∠ABN+∠EAB=180°.因为∠EAP+∠BAD=180°，∠EAB+∠PAD=180°，所以∠ABN=∠PAD，故有△ADP≌△BAN，所以DP=AN=2AM.

再次融入夹角问题，提升全等的应用价值，渗透分类讨论的数学思想，设计出如下问题.

问题10 如图11，在变式9的条件下，试探究DP与AM的夹角度数是否为定值.

分析 如图16，延长MA交PD（或PD的延长线，如图17）于点O，都有∠PAO+∠EAN=120°.因为BN∥AE，∠EAN=∠ANB=∠OPA，所以∠PAO+∠OPA=120°，∠POA=60°，所以DP与AM的夹角度数为定值60°.

3 专题构建

以含60°角的菱形为图形载体，以全等的应用与拓展为主线，以几何画板等教学软件动态呈现，构建一题一课专题教学.

例如，对于基础一般的班级，可将问题1，2安排为前置练习，了解学生对全等知识的掌握情况;通过问题4创设情境，熟练全等解题的一般方法;通过问题5，6变式拓展，引导学生深入探究，小组合作交流，提升应用技能.通过专题课的学习，学生能够从不同的问题情境中，根据已有条件分析、思考、联想，通过合理构造辅助线，应用图形全等解决与边角相关的综合性问题.

又如，对于基础较好的班级，可将问题1安排为前置练习，熟练全等的应用方法;通过问题4创设情境，问题5，6横向变式，深化技能;进而引导学生探究解决问题7，体会知识的本质，以及多考点的紧密联系;最后学生深度探究问题9，小组合作挖掘多种解法，交流展示;问题10安排为课后思考题.通过专题课的学习，让学生掌握将表面上与全等无关的问题转化为求线段或角相等的问题，进而应用全等解题的通性方法，提升数学应用意识和创新思维能力.

参考文献

[1]苏国东.例谈线型伴随轨迹问题[J].数理化解题研究，2022（02）：20-21.

[2]刘莎.弱化“模型”重视数学分析[J].数理化学习（初中版），2020（02）：20-23.

作者简介

苏国东（1986—），男，广东广州人，中学一级教师;广州市十佳数学教师、市特约教研员、市中心组成员、市名师工作室成员、荔湾区名教師等;主要研究信息技术与数学教学融合;发表论文多篇.