凸显转化思想，提高课堂实效

王芳

[摘  要] 转化思想是一种重要的数学思想方法，文章以“除数是小数的除法”的教学为例，提出凸显转化思想，提高课堂实效的路径，即创设情境，激发学生认知冲突;适时启发，培养转化意识;经历过程，体验转化思想。

[关键词] 转化意识;转化思想;课堂实效

转化思想是一种重要的数学思想方法，在教学中渗透转化思想，可以帮助学生厘清知识结构与脉络，有利于学生理解数学知识本质，对于实现学生高效学习具有重要意义[1]。笔者以“除数是小数的除法”为例，立足转化思想，尝试进行积极的教学实践，期望引发广大教育同仁的借鉴和思考。

一、创设情境，激发学生认知冲突

学生是课堂的主人，教学中，教师可利用小学生好奇心强的性格特点，创设情境，精心设疑，制造悬念，使学生处于一种“心求通而未达，口欲言而未能”的不平衡状态，进而使他们积极主动地参与到学习当中，提高课堂效率。

师：笑笑妈妈到水果店买了6千克苹果，一共花了7.2元，那么每千克苹果多少元钱？

（学生列式子计算，并汇报交流。）

生1：应该列式为7.2÷6。

师：除数是整数的小数除法是怎样计算的？

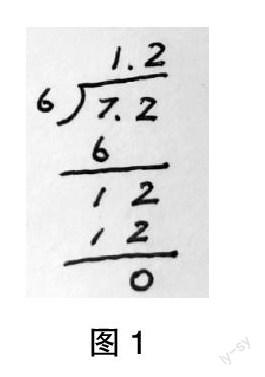
生1：在计算除数是整数的小数除法时，应该先按照整数除法的计算方法进行，把商的小数点和被除数的小数点对齐。（见图1）

师：对，这是我们上节课学习的内容。现在我们再来看这样一道题，鸡蛋的价格是每千克4.2元，笑笑妈妈买鸡蛋一共用了7.56元，那么笑笑妈妈一共买了多少千克鸡蛋？

生1：这题也应该用除法，根据总价÷单价=数量，应该列式为7.56÷4.2。

师：请同学们比较“7.2÷6”和“7.56÷4.2”这两个式子，看看它们有什么区别？

生1：第一个式子我们已经学过，除数是整数，而第二个式子除数是小数，这种式子的计算方法我们还没有学过。

生2：我刚才尝试着直接按照除数是整数的小数除法进行计算，发现根本行不通。

师：这就是我们这节课要解决的问题。

教学中，教师从学生已有的知识经验出发，通过创设情境使学生复习旧知识，从而为学生的新旧知识转化奠定知识基础。在此基础上，引导学生列出除数是小数的除法算式，使学生感受到除数是小数的除法与先前的内容有很大不同，用既有的知识难以解决新问题，从而引发学生的探究需要，激发学生的探究意愿。

二、适时启发，培养转化意识

当面对新问题时，小学生往往会由于缺乏思维经验在解题时左冲右突、不得章法。此时，教师在学生的思维“盲区”适时启发，能够起到“一语惊醒梦中人”的教学效果。

当学生在探索7.56÷4.2的算法时，教师为他们讲述了“曹冲称象”的故事。在讲完故事后，教师设计了这样的教学环节：

师：大象很重，当时没有足够大的秤，曹冲是怎么办的呢？

生3：曹冲建议把大象带到一艘大船上，船承重之后会下沉，这时在船的边上刻下记号，然后将大象换成石块，使船沉到记号处，这样称出的石块的重量就是大象的重量。

师：对，聪明的曹冲把大象的重量转化成了石块的重量，从而顺利地解决了问题。这对我们有什么启发呢？

生4：把未知的问题转化成已知的问题，把复杂的问题转化成简单的问题。

师：我们是不是也应该尝试用转化的办法解决7.56÷4.2的计算问题呢？

（学生恍然大悟。）

转化思想本身并不难理解，然而問题的关键是如何让学生主动想到运用转化的策略解决问题，这才是教学的根本任务。教学中，教师采取了讲故事的办法，既激发了学生的学习兴趣，又能够使学生从故事中得到某种启发，从而自主地想到转化策略。

三、经历过程，体验转化思想

数学思想具有一定的抽象性，要使学生深刻领悟数学思想，就必须让学生经历曲折的探索过程，让学生对数学思想方法的感悟沉淀、凝聚在这些数学结论上，只有这样，学生才能在掌握数学知识的同时，领悟数学思想方法[2]。

1. 实现转化

师：既然我们已经明确了可以用转化的思想解决问题，那么，应该如何实现这种转化呢？

生5：我可以把7.56元和4.2元都转化成以角为单位的数，7.56元=75.6角，4.2元=42角，把原来的算式“7.56÷4.2”转化成“75.6÷42”，这样就把新知识转化成我们已经学过的知识了。

师：这种转化依托于具体的情境，按照元角之间的关系进行转化。但是，如果算式脱离了这种具体情境，又应该怎么办呢？

生6：我们也可以利用商不变的规律进行转化。

师：对。我们可以通过一组式子来复习“商不变的规律”。（出示图2）

师：让我们一起回忆商不变规律的内容。

生（齐）：被除数与除数同时乘或除以同一个数（不为零），商不变。

生7：把被除数和除数同时扩大10倍，算式就变成了75.6÷42，这样就变成了我们已经学过的除数是整数的小数除法了。

师：对。通过商不变的规律，把除数是小数的小数除法转化成除数是整数的小数除法，正是转化思想妙用的生动体现。

生8：我是这样转化的。把被除数和除数同时扩大100倍，这样算式就变成了756÷420，这样得出的结果是一样的。

师：“75.6 ÷42”和“756÷420”这两种转化方式，究竟哪一种更好一些呢？

（学生讨论。）

生7：我认为把除数转化成整数就可以了，被除数是不是整数无关紧要。而且如果要把被除数也转化成整数，就会导致数据变大，算起来比较麻烦。

师：请同学们看下面的式子，0.756÷4.2，如果要把被除数和除数都转化成整数，就需要把被除数和除数同时扩大1000倍，这样就变成了756÷4200，数据变得很大，计算量也变大了。

生8：那只把被除数变成整数可以吗？

生7：不可以，之所以要进行转化，就是因为除数是小数。如果只把被除数变成整数，而除数依然是小数，这样的话我们还是不能计算呀！

师：通过上面的分析，我们认识到，要运用商不变的规律，先把除数变成整数，再进行计算。

教学中，教师引导学生实现了从未知到已知的转化。在这个过程中，教师围绕“如何转化”这个问题引导学生对两种转化方法展开对比、辨析，使学生意识到被除数是不是小数是无关紧要的，只要把除数转化成整数就可以了，从而使学生掌握正确的转化方法。

2. 探究算法

师：实现了由未知向已知的转化，现在同学们能试着解决问题了吗？请同学们尝试用竖式进行计算。

（学生探索算法，教师巡回指导。）

教师展示如下几种算法（如图3）。

师：这是刚才同学们在计算过程中出现的不同算法，请大家进行评判，究竟哪种算法是正确的？

生9：第①种算法不对。商的小数点应该与被除数对齐。

生10：商的小数点不是已经和被除数对齐了吗？

生9：这里说的被除数指的是转化后的被除数，也就是1.8中的小数点要和转化后的被除数75.6中的小数点对齐，而不是与7.56中的小数点对齐。

师：你能具体说一说其中的原因吗？

生9：因为在把除数转化成整数后，原来的算式变成了75.6÷42，而根据除数是整数的小数除法的算法，应该把商的小数点与被除数的小数点对齐，因此，这里的被除数指的是转化后的被除数。

师：明确了商的小数点如何确定，我们再来看第②种算法是否正确。

生10：第②种竖式算法也不对。因为竖式中间的小数点不需要写。

师：为什么？

生10：因为竖式中间的336指的是336个0.1。

师：第③种竖式算法有问题吗？

学生一致认为第③种竖式算法是正确的。

师：现在，同学们能总结一下除数是小数的小数除法的计算法则吗？

生（齐）：先运用商不变的规律，把除数是小数的小数除法转化成除数是整数的小数除法，然后按照除数是整数的小数除法进行运算，商的小数点要与转化后的被除数的小数点对齐。

教師先让学生自己尝试计算，主动积极地思考，从而使学生不同的思考过程得以展示出来，竖式计算呈现出多样化;然后引导学生围绕“商的小数点的位置应该怎样确定”“竖式中间的小数点用不用写”这两个问题展开辨析，从而使学生获得对除数是小数的除法笔算的准确理解。

3. 总结反思

师：让我们一起回顾问题解决的整个过程，你认为其中最关键的是什么？

生11：最关键的是转化的思想。

生12：转化的方法真奇妙，它让复杂的问题变得简单。

师：对。转化既是一种重要的数学思想方法，又是一种解决问题的基本策略。它能化难为易、化繁为简、化未知为已知。

美国心理学家波斯纳说：“没有反思的经验是狭隘的经验， 最多只能是肤浅的知识。”教师引导学生对问题解决过程进行回顾和反思，可以使学生深刻体验到转化思想在问题解决中的重要作用，从而增强学生对转化思想的把握和领悟。

在数学教学中，教师要重视转化思想的渗透，引导学生把未知化为已知，把复杂化为简单，让学生在运用转化思想解决问题的过程中，加深对知识和转化思想的理解，从而使数学教学更加高效。

参考文献：

[1]  石景飞，于正军，张秀花. “除数是小数的除法”教学实录与评析[J].小学数学教育，2021（11）：66-68.

[2]  张仁进. 例谈教学中的“圈养”和“散养”：以“除数是小数的除法”一课为例[J]. 基础教育参考，2020（04）：54-57.