以“画”促“化”

吴华平

摘要：画图是运用图形的重要方式之一，可以把抽象的语义表征转化为形象的图形表征，帮助学生对已学的概念进行分类、整理和内化，进而理解概念的本质。《趣HUA集合图》一课，利用图示（集合图）的方法来表达数学知识之间的本质联系，可以使隐性的知识外显化、可视化，便于学生思考、理解和表达。课堂教学中，学生通过动手“画图”，并有条理地“话图”，最终实现了认知的“数学化”。

关键词：画图；几何直观；集合图；数学化；小学数学

一、教学意图与目标

《义务教育数学课程标准（2011年版）》将“几何直观”作为十大核心词之一。《义务教育数学课程标准（2022年版）》依然将“几何直观”列为数学核心素养的主要表现之一，提倡运用图形描述和分析问题。画图是运用图形的重要方式之一，可以把抽象的语义表征转化为形象的图形表征，帮助学生对已学的概念进行分类、整理和内化，进而理解概念的本质。对此，我们开展了“趣HUA数学”的研究与实践，并自编了系列学材。《趣HUA集合图》就是其中的一课。

本节课的教学安排在五年级学生学习了方程、等式、质数、因数、倍数等诸多概念之后。数学概念之间的关系比较复杂，有的是交叉关系，有的是并列关系，还有的是包含关系，这些对于小学生而言显然比较抽象，难以理解与掌握。这也导致学生在判断“一个数不是质数就是合数”“一个算式不是方程就是等式”等问题时，错误率总是很高。而如果利用图示（集合图）的方法来表达数学知识之间的本质联系，则可以使隐性的知识显性化、可视化，便于学生思考、理解和表达。

本节课的教学目标如下：在具体情境中，亲历集合图的产生过程，会画图表示两个量之间的关系；能理解集合图每一部分的含义，用自己的语言描述两个量之间的关系，并能解决生活中稍复杂的实际问题；能在概念的整理应用中，不断沟通概念之间的联系，初步体会集合图的价值和模型思想。

二、教学过程与说明

（一）唤醒经验，体验一个量的表示方式

师五（1）班参加跑步的有6人，如何简洁地表示这个量？

生（展示画法，如图1所示）可以画一条线段图来表示。

生（展示画法，如图2所示）可以画一个圆圈来表示。

师两种表示方法都很直观、简洁。你是怎么想到用圆圈表示的呢？

生前面的学习中，我发现数学书上常常用一个圆把一些物体圈起来。

师的确，（出示图3）数学上我们通常用一个圈来表示一个整体。

［说明：五年级学生在过去的学习中，已经接触了一些有关集合的知识。比如，认识11—20各数时，把10根小棒捆成一捆，再圈一圈，这10根小棒就是一个整体，这样圈可以看得更清楚。再如，认识分数时，把一些物体圈起来表示一个整体并平均分。基于学生已有的学习经验，课始创设一个简单的情境，让学生用简洁的方法表示一个量，感受一个指定的对象集中在一起就是集合，使后续的学习有了生长点。］

（二）趣HUA集合图，促进学生思考

1.“画”集合图，让思维可视

师五（1）班的体育社团中，参加跑步的有6人，参加跳远的有5人。学校打算给他们每人准备一套运动服，一共要买几套？

生11套，6加5等于11。

师一定是11套吗？想一想，说一说。

生有可能比11套少。

师小于11套是什么情况呢？

生可能有同学两个项目都参加了。

师看似简单的“一共要买几套运动服”的数学问题，实则并不简单。能不能把你们的想法画出来，让大家一目了然呢？

（学生画图。）

师（展示学生画法，如图4所示）能说说这个图表示什么意思吗？

生2个圆分开摆放，表示跑步的同学中没有参加跳远的，跳远的同学中也没有参加跑步的，所以用算式表示为6+5=11（人）。

师真好！看着画好的图，我们一眼就能发现它们之间的关系，从而算出一共要买多少套运动服。（展示学生画法，如图5—图7所示）这里还有3位同学的作品，谁能看懂这些图的意思？

生前两幅图表示的都是有2人既参加了跑步又参加了跳远，只是一个用的是线段图，一个用的是长方形。

生我觉得长方形这个图看得清楚一些，重复的2个人只画了一次。

生第三幅图表示的是有1个人重复了，他把两个圆交叉起来，左边的圆表示跑步的共有6人，右边的圆表示跳远的共有5人，中间交叉部分就是那个既参加跑步又参加跳远的1人，所以有5+6-1=10（人）。

生為什么要减1呢？

生因为那1个人被重复加了，所以要减掉。

生第三幅图，看上去跑步的好像有7人，跳远的好像有6人，容易产生误解，我觉得不太好。

师（出示图8）老师也带来了一幅图，谁能看懂这幅图的意思？

生左边的“3”表示只参加跑步的人数，右边的“2”表示只参加跳远的人数，中间的“3”表示既参加跑步又参加跳远的人数。图让我们一下子看清了较复杂的数量之间的关系。

生我还能对着图说出两道算式的意思呢。3+3+2=8，是把三部分的人数合并起来；6+5-3=8，是先把两个圈里的人数加起来，再去掉重复的3个人。

师说得真好！大家想一想，重复的可能会有几人？

生1人、2人、3人、4人、5人。

生不可能出现中间重复的有5人。

生我认为重复的有可能是5人。大家看，（展示画法，如下页图9所示）我是这样画的。

生（展示画法，如图10所示）我也觉得有可能是5人。

生这两幅图，一个是用点表示人数，一个是用数表示人数，它们表达的意思是一样的。

生从这两幅图中，我看出跳远的那5个人同时都参加了跑步，最右边的空白部分其实一个人也没有。

师那我们能不能让这个图表示得更清楚一点呢？跟同桌商量商量。

（学生同桌讨论。）

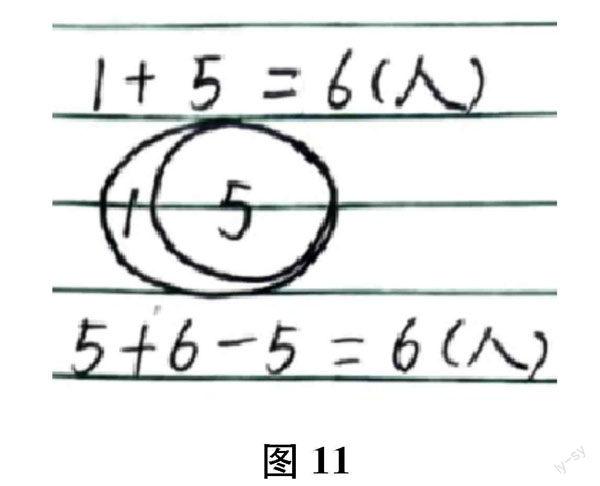
师（出示图11）这个图是不是比刚才更清楚了？你读懂了什么？

生当两个圈重合得越来越多时，跳远的小圈里的人就慢慢全跑到跑步的大圈里去了。这时表示跳远的5人都参加了跑步。

生外面的大圈表示参加跑步的有6人，里面的小圈表示两项都参加的有5人，也就有1人只参加了跑步。

［说明：对于小学生来说，上述有重叠关系的问题比较抽象。让学生画图表示两种量的不同情况，旨在帮助他们借助图形直观理解数量之间的关系，让思维可见，从而化难为易。随着两个圆的位置关系不断变化，两种量的关系由并列到交叉直至包含，学生的思维越来越全面。画图是解决问题的一种工具，学生在画的过程中也在观察、比较、分析，不断地体验、感悟、调整，进而能更准确地表示两个量之间的关系，让思维变得更严谨。］

2.“话”集合图，让表达有条理

师刚才我们通过画一画、说一说，解决了买运动服的问题。（出示图12）老师这儿还有一幅图，你能对着图讲一个生活中的数学问题吗？

生在六一节班级联欢会上，唱歌的有10人，跳舞的有8人，两项都参加的有3人。

师这不是问题。你能提出一个数学问题并解决吗？

生一共有多少人参加表演？10+8-3=15（人）。

生只参加唱歌的有几人？10-3=7（人）。只参加跳舞的有几人？8-3=5（人）。

生郊游时，带饮料的有10人，带水果的有8人，两样都带的有3人。

……

师看，同样的图，同样的数据，我们能讲出这么多不同的故事，但不同的故事反映的是同样的数量关系。（出示图13）这儿还有一幅图，你也能讲个故事吗？

生乐器社团中，会吹笛子的有18人，既会拉二胡又会吹笛子的有10人。

师你也能提出一个数学问题吗？

生只会吹笛子的有几人？

生只会吹笛子的有8人，18-10=8（人）。

生五（1）班喜欢看动画片的有18人，既喜欢看动画片又喜欢看科幻片的有10人。“18-10”就是只喜欢看动画片的人数。

……

［说明：语言是思维的外壳，想得清楚才能说得明白。让学生看集合图创编实际问题并自主分析解决，可以以画促思，以思促话。同样的图编出不同的故事，实现了由一到多，培养了学生有条理表达的能力和思维的灵活性。］

3.“化”集合图，让认知结构化

师（出示图14—图17）这些是部分教材中曾经出现的集合图，请说说这些图表示的意义。

（学生交流。）

师生活中我们常常用这样的集合图表示两个量之间的相互关系。（指图16）比如刚刚看的这一幅图，我们可以用它来表示等式和方程的关系。你还想到用这样的图来表示什么？

生我想用它来表示三角形和直角三角形的关系。

生我想用它来表示长方形和正方形的关系。

……

（学生继续说哪些概念之间的关系也可以用图14、图15、图17这样的图来表示。）

师看来集合图在我们的学习中随处可见，它能直观地表示出两个量甚至是多个量之间的关系。

［说明：前面的“画”“话”，最终是为了更高层次的“化”做铺垫。这里的“化”，主要指数学化。教学中，再现学生曾经见过的集合图，引导他们思考还有哪些概念之间的关系也能用同样的图来表示，沟通知识之间的联系，凸显知识的本质，完成纵向数学化，培养思维的深刻性。］

（三）应用集合图，促进深度理解

師用集合图表示下列题中数或式之间的关系，并和同桌说一说。

（1）①2的倍数：2、4、6……；②3的倍数：3、6、9……。

（2）2、3、4、7、9、11、12。

（3）①5+3=8；②x+3=28；③15-A=24；④27÷3=9；⑤16×4=64；⑥ △-9=122。

生第（1）题，我们可以画两个交叉的圈，因为2和3有公共的倍数。

生第（2）题，我把这几个数分成了奇数和偶数。

师那该画一个什么样的集合图表示它们的关系？

生画两个分开的圈，因为一个数是奇数就不可能是偶数。

生我把他们分成了质数和合数，画的图也是分开的两个圈，因为是质数就不可能是合数。

生第（3）题这些等式中的②③⑥都是方程，可以画一个大圈套一个小圈，因为所有的方程都是等式。

［说明：练习设计是在学生学过了方程、等式、倍数、奇数和偶数等多个概念以后，作为单元整体建构的延伸，试图让学生在应用中不断沟通概念之间的相互联系，再次体验集合思想，培养思维的创造性。其中，第（2）题具有一定的开放性。］

（四）回顾与反思

师同学们，今天我们是怎样解决问题的？

生我们通过画图、讨论、联想解决了一些实际问题。

师当我们解题有困难的时候，可以画一画；进行知识的归类整理时，也可以画一画……借助HUA图，我们能想得更清楚、说得更明白、理解得更深刻。

［说明：通过回顾与反思，帮助学生积累活动经验，引导学生进一步体会画图策略的意义与价值，做好学习方法的储备。］

本节课通过生活中常见的重复问题，制造认知冲突，引发学生画图的需要。让学生把抽象的关系通过图示表征出来，使学生的思维外显化、可视化；让学生用自己的语言去描述图意，力求让学生的表达更加条理化；借助集合图，将前面所学的概念加以辨析、分类与整理，让学生的认知结构化，理解更加深刻。此外，本节课通过同样的图让学生联想不同事物之间的相同关系，培养了学生的发散思维；再让学生把不同事物之间的相同关系用本质相同的图表示，培养了学生的模型意识。课堂中，学生有创意地“画”，有个性地“话”，有深度地“化”——通过动手“画图”，并有条理地“话图”，最终实现认知的“数学化”。