以数学思想引领公式探究

金雪强

摘要：数学教学不仅应该让学生“知其然”，还应该让学生“知其所以然”。圓的知识与学生以往学习的直线图形的知识有着较大的差异。对于学生而言，从直线图形的学习转向曲线图形的学习，不仅仅是学习内容的转变，更面临着思维方式的转变。教师可以数学思想引领学生开展公式探究，使其在旧知的基础上推理出新的知识——圆的面积计算。具体地，可以类比思想引出探究思路，用转化思想开展探究过程，借极限思想得出探究结论，展应用意识深化探究成果。

关键词：小学数学；《圆的面积》;类比；转化；极限

圆的面积有着固定的计算公式，学生只要记住公式就能轻松地完成计算，因而有些教师并不把“圆的面积”作为小学数学的重点内容展开教学。但是，数学教学不仅应该让学生“知其然”（知道圆的面积计算公式），还应该让学生“知其所以然”（探究圆的面积计算公式的推导过程）。圆的知识与学生以往学习的直线图形的知识有着较大的差异。对于学生而言，从直线图形的学习转向曲线图形的学习，不仅仅是学习内容的转变，更面临着思维方式的转变。教师可以数学思想引领学生开展公式探究，使其在旧知的基础上推理出新的知识——圆的面积计算。相关的教学过程与思考如下：

一、教学过程

（一）以类比思想引出探究思路

师某同学和妈妈一起购买一块圆形的玻璃来装修卧室。玻璃按面积定价，那圆形玻璃的面积应当如何计算呢？帮助这位同学解决这一问题，要用到我们今天要学习的内容——圆的面积计算。学习圆的面积计算之前，我们先来回顾一下：之前我们学过哪些平面图形？它们的面积计算公式是什么？这些公式又是怎样推导出来的？先来说说长方形的面积。

生长方形的面积计算公式是长乘宽。我们是通过数方格的方法知道的，比如先数一行有6个方格，再数有4行，一共就有6乘4等于24个方格，所以长方形的面积计算公式就是长乘宽。

师我们是通过数方格也就是数面积单位的方法得到长方形的面积计算公式的。（出示图1）把圆放到方格纸中，你能用数方格的方法算出它的面积吗？

生小扇形大约是12.5格，整个圆就是50格，即50平方厘米。

师真棒！但这好像得不到圆的面积计算公式。不急，我们继续回顾：我们是怎么研究平行四边形的面积的？

生我们是将平行四边形转化成长方形来研究的。

师也就是说，研究平行四边形的面积时，我们将平行四边形的面积转化成长方形的面积。那么，三角形和梯形的面积呢？

生都是转化成平行四边形的面积。

师是的，在平行四边形、三角形和梯形面积计算公式的推导中，都蕴含着一个重要的数学思想——转化，将“未知”转化为“已知”。而一般我们研究一个新的未知的图形时，也常常是将它转化成研究过的已知的图形。

［说明：课始，教师带领学生复习以往所学的几何知识，类比以往学过的长方形、平行四边形等图形面积计算方法的得出过程，发现圆的面积计算方法的研究思路——转化。］

（二）用转化思想开展探究过程

师那么，圆能转化成什么图形呢？

（学生小组讨论。教师选择典型思路展示交流。）

生我们组想把圆转化成平行四边形。（展示做法，如图2）我们将圆沿直径剪开，再对半剪开，分成四个扇形，然后拼在一起。但这只是一个近似的平行四边形。

师为什么说是近似的呢？

生它的上、下两条边是弯曲的，不直。

师有什么办法能够让这两条边变直呢？

生可以再多剪几刀，应该会更像平行四边形。

师（课件演示把圆平均分成16份，再进行拼接）确实更像平行四边形了，但好像还是不直，还是有缝隙。我们可以怎么办？

生继续分成更多份。

［说明：发现可用转化思想研究圆的面积计算方法之后，让学生充分发挥主观能动性，探究可以转化的图形。学生有的参考“割圆术”的思路，将圆转化为正方形、正六边形；有的类比将平行四边形剪拼成长方形的思路，将圆剪拼成平行四边形……对此，教师选取学生的典型思路展示交流，明确转化的方向。］

（三）借极限思想得出探究结论

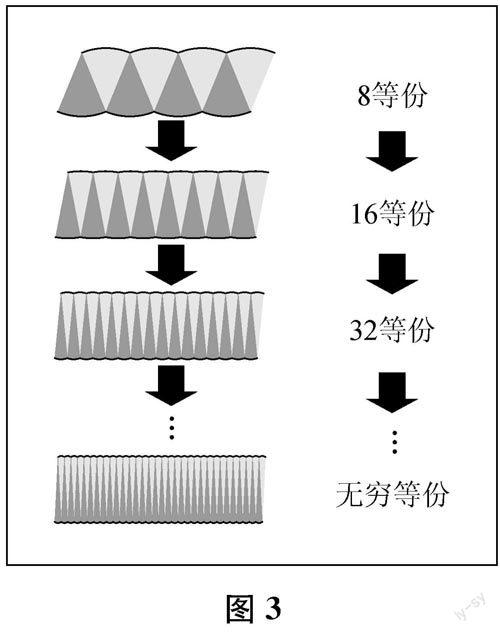
师（课件展示继续等分圆的过程，最终定格于下页图3）可以看到，分割的份数越多，拼接成的新图形上的缝隙就越小，该图形就越像平行四边形。现在我们考虑一种理想化的情况：假如我们分割圆时，分割的份数是无限的，那么它所拼接成的新的图形上的缝隙就是无限小的，即边是无限接近于直线的，新图形的面积就是无限接近于圆的。此时，拼成的是一个什么图形？

生长方形。

师（出示图4）让我们来看一看拼成的长方形的长与宽和原本的圆有什么联系。

（学生经过观察发现规律，纷纷回答：拼成的长方形的长是圆周长的一半，宽是圆的半径。）

师那么应该如何计算圆的面积呢？

生圆周长的一半可以用πr表示，所以，圆的面积=拼成的长方形的面积=长×宽=πr×r=πr2。

［说明：当学生意识到需要把圆平均分成更多的份数，才能让拼成的平行四边形的一组对边越来越直，所以利用极限思想把圆平均分成无数份，就可以拼成一个直的平行四边形（长方形）时，圆的面积计算公式的推导也就顺理成章了。］

（四）展应用意识深化探究成果

师现在让我们回到课始提出的问题：要帮助那位同学计算圆形玻璃的面积，我们需要知道哪些条件？用到哪些工具？

生要计算圆形玻璃的面积，需要知道它的半径。由于这个圆形玻璃的圆心很难准确地确定，因此很难通过直接测量得到它的半径。根据本节课我们探究的结果，可以用卷尺测量出这个圆形玻璃的周长，以公式反推出这个圆形玻璃的半径，然后用圆的面积计算公式来计算该圆形玻璃的面积。

［说明：课尾，让学生应用本节课的探究成果解决课始提出的问题，首尾呼应，形成完整的教学闭环。这不仅能够促进学生进一步深化本节课的学习内容，还能有效发展学生的应用意识。］

二、教学思考

《圆的面积》一课的教学重点绝不仅仅是让学生记住圆的面积计算公式以及会用公式解决现实问题，更应当帮助学生养成数学思维，学会运用数学思想。

圆的面积计算看似和以往学习的知识都毫不相干，但是，教师引导学生把圆这个陌生的图形转化成以往学过的熟悉的图形，通过用已有知识计算熟悉的图形的面积反推如何去计算圆这个相对陌生的图形的面积。这样，促进学生养成一种类比思维——面对陌生的数学问题时，把“陌生”和“熟悉”相联系，去已有的“武器库”中寻找解决问题的“武器”。

而本节课中，一种重要的“武器”就是转化思想。类比之前平面图形面积计算公式学习的经验，学生会想到将圆转化为平行四边形、长方形、三角形、梯形等。教师选取典型的平行四边形为探究的主线，引导学生开展深度探究。通过寻找剪拼成的平行四边形（长方形）与原来的圆的关系，总结圆的面积计算的一般性规律，学生自主推导出了圆的面积计算公式。这让学生既知其然——知道如何计算圆的面积，更知其所以然——知道为什么这样计算圆的面积。学生学会推理得到公式的方法，从某种意义上说，比学生会使用公式解决现实问题更为重要。

尽管历史上人类探索圆的面积计算公式的方法不同，但是不同中蕴藏着相同——都希望“化曲为直”，即把圆这个曲边图形转化为直边图形；而且在解决问题的具体过程中，都不可避免地涉及“无限接近”，即极限思想——这也是本节课所要渗透的一种重要的数学思想。对此，教师从学生的4等分作品出发，用儿童化的语言——消除缝隙、使直线变平，帮助学生感受化曲为直过程中的极限思想。

能运用所学的知识解决生活中的问题，是检验学生真正学会知识的重要标准，也是学以致用的具体表现。《义务教育数学课程标准（2022年版）》也继续强调了学生应用意识的培养。本节课尾，教师呼应课始的问题，引导学生应用本节课所学解决生活中的问题，帮助学生养成理论联系实际的习惯，发展实践能力。

参考文献：

［1］ 刘加霞，张殿军.数学表现性评价任务及其量规的设计与运用——以“圆的认识”为例［J］.小学教学（数学版），2021（2）.

［2］ 邵虹.找准学习起点，捕捉思维动态，渗透极限思想——“圆的面积”教学实践［J］.小学教学（数学版），2018（12）.

［3］ 裴樹栋.“烙饼问题”要教学“计算公式”吗——由“饼烙问题”教学引发的思考［J］.中小学数学（小学版），2015（1/2）.

［4］ 车前.在公式推导中渗透数学思想——《圆的面积》新授课教学回顾［J］.教育研究与评论（小学教育教学），2016（11）.5，21，24，31，33，48，57，58，60，75，79-83，86