结构静弹性问题的双互易边界元法

潘先云，周枫林，王瑾元，袁小涵，钦 宇

（湖南工业大学 机械工程学院，湖南 株洲 412007）

1 研究背景

结构静弹性问题研究结构在受到外力作用下而产生的应力、应变和位移的变化，以维持结构在合理变化范围之内，保证应用场景的安全性，为工程设计提供参考。如裴智毅等[1]运用弹性力学对钢桥面铺装层进行了应力分析，为钢桥面STC（super-through concrete）铺装的设计和箱梁横隔板截面尺寸的选取提供了参考；郭一竹等[2]研究了弹性伸杆的力学性能，并且对其刚度进行了分析。结构静弹性问题分析的数值方法以有限元法（finite element method，FEM）[3-5]为代表，其中心思想是将连续的弹性体离散为有限个单元，再根据弹性力学基本方程和变分原理建立单元节点间位移与力的关系，形成单元刚度矩阵，然后将所有单元刚度矩阵整理成总体刚度矩阵，最后通过引入边界条件，生成关于未知节点位移的线性方程组。ABAQUS、ANSYS等有限元法仿真软件的出现，使有限元法变得简单高效，并在机械结构分析、土木工程领域得到了广泛应用。但是，有限元法仍存在不足之处。首先，该方法需要将整个结构区域进行离散，处理的数据量较大，计算时间较长；其次，难以精确处理无限域和应力集中等问题，上述缺陷影响了有限元法的精度和实际应用范围。因此，研究者在有限元法的基础上发展了一种新的数值计算方法：边界元法[6-8]（boundary element method，BEM）。相比于有限元法，边界元法只需要对边界进行离散，不涉及域内，因而将问题的维数降低，拥有较高的计算效率和计算精度。边界元法在弹性力学中有许多研究成果和成功案例。如曾华等[9]利用双互易边界元法求解了弹性问题，证明其具有较高的精度；徐俊祥等[10]采用直接边界元法对弹性体整个域内的位移场和应力场进行了求解。边界元法在其它领域也有着广泛应用。

本文运用双互易边界元法（dual reciprocity boundary element method，DRBEM）分析结构静弹性中含有体力项的非齐次问题，以及在无解析解的实际工况下，通过双互易边界元法和有限元法分析结果进行对比，验证双互易边界元法在分析结构静弹性问题上的有效性和精确性，并为处理非齐次弹性力学问题提供一种新的方法。有学者曾对边界元法和有限元法进行了对比研究，比如豆中强[11]利用有限元分析软件——ANSYS软件和边界元法求解二维弹性静力学问题，并将求解得到的结果与精确解进行对比；周枫林等[12]分别用有限元法和边界元法分析了印刷机滚筒结构刚度，证明了边界元法是用于结构刚度分析的一种高效方法。与上述研究的不同之处在于，本研究采用指数型基函数作为双互易边界元法的插值函数，对结构进行静弹性力学分析，验证该方法的有效性，并将DRBEM和FEM对比，验证DRBEM在实际工况下结构静弹性分析中的精确性。

2 静弹性力学双互易边界元法

2.1 静弹性力学的理论基础

课题组采用双互易边界元法，分析正方体模型在受外力载荷条件下引起的弹性变形情况。

三维静弹性力学问题的基本方程如下：

平衡微分方程为

几何方程为

物理方程（本构方程）为

式（1）～（3）中：i,j,k=1, 2, 3；

σ为应力；

b为体力；

u为位移；

δ为Kronecker函数；

G为剪切模量；

λ为拉梅常数，且

其中，E为弹性模量，v为泊松比；

ε为应变，且

将式（2）代入式（3）中，得到如下应力分量用位移分量的表示：

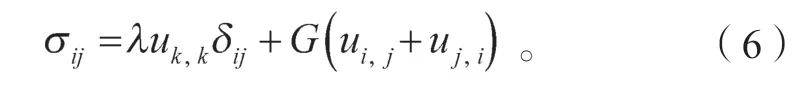
再将式（6）代入式（1）中，可得到如下用位移表示的平衡方程（Navier方程）：

2.2 静弹性力学双互易边界元法描述

上文得到用位移表示的平衡方程如下：

位移边界条件为

面力边界条件为

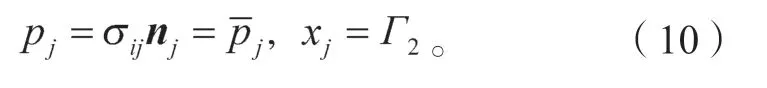
式中：n为边界外法向量；

Ω为弹性体所占区域；

Г1和Г2分别为位移边界和面力边界；

可用加权余量法、功的互等定理等建立边界积分方程，现利用加权余量法、散度定理将式（1）、（9）和（10）建立弹性力学边界积分方程，简化后如下：

其中，r为场点与源点之间的距离，l=1, 2, 3；

式中，θ为源点处的立体角，

式（11）是在bj=0情况下的边界积分方程，也就是计算域内没有外力作用，式（12）存在体力项。式（11）和（12）描述的是已知边界Г上位移uk和面力pk计算区域内所有点p在k方向上的位移。

对于边界积分方程式（12）中含域内体力积分非齐次项问题，利用双互易方法处理。用径向基函数对式（12）中的体力项进行插值拟合，插值表达式为

式中：φj为插值函数；

H和L分别为边界点和内部点的数量。

值得注意的是，若体力项函数未知，则径向基函数插值系数也将是未知的。找到径向基函数对应式（7）特定的位移u满足：

利用分部积分可以将式（12）转换为完全边界积分方程：

m=1, 2, 3。

边界积分方程式（11）和（18）只有边界积分，所以可以通过离散边界进行求解计算，将位移和面力离散为如下形式：

M为每一个单元的节点数量。

将计算边界Г离散为N个边界单元，再将式（19）和（20）代入式（11）和（18）中，得到离散形式的边界积分表达式如下：

式中：Γf为第f个单元的边界。

最终离散后式（21）和式（22）可形成如下线性代数方程组：

将所有未知量移到方程的左边并整理可得

通过式（25）所示代数方程组可以求出所有边界节点的未知量，包括面力和位移。

2.3 指数型插值函数及其特解

本文采用指数型插值函数作为双互易边界元法的径向基函数，对体力项进行插值拟合，指数型插值函数表达式如下：

式中：c为形状参数；

r为场点Q到源点P之间的距离，且

对应的指数型插值函数在弹性问题上的位移特解表达式为

式中：

其中：

上述位移特解并不是唯一的。该位移特解是通过Papkovich势函数法推导出来的满足平衡方程的一种形式，并且保证了g(r)与q(r)在全域内连续且有一阶导数。不同的RBF对应的特解也会改变，将位移特解导入胡克定律与平衡方程，同样可以求解出应变、应力和位移特解。

3 数值算例

为了验证双互易边界元法在静力学分析上的有效性和准确性，设计了两个算例。第一个算例是有解析解情况下，通过DRBEM方法得出数值解与解析解对比，验证双互易边界元法的有效性。第二个算例是在无解析解的实际工况下，将DRBEM结果与有限元分析软件结果进行对比，进一步验证双互易边界元法的有效性和准确性。

根据对指数型基函数作为双互易边界元法的径向基函数的分析研究，当指数型基函数的形状参数c=0.2时，数值计算精度最高，所以本文算例双互易边界元法中，指数型径向基函数形状参数c取0.2。

3.1 球体边界元静力学分析

本算例研究半径为2 mm的球体，笛卡尔坐标中心为球心。球体的材料参数设置如下：密度为1.14 t/mm3；泊松比为0.25；杨氏模量为1 000 MPa。通过双互易边界元法对球体进行弹性力学分析，其网格划分如图1所示，网格数量为2 250个。

图1 球体网格划分Fig.1 Sphere meshing

通过改变网格大小、增加网格数量，计算得到节点上面力以及域内应力的数值解，将其与精确解对比得到相对误差，精确解是通过控制方程式（8）得到的，其中相对误差定义为

式中：v为相关变量；

为精确解；

为数值解；

|v|max为精确解中的最大值；

N为节点数量。

在边界元法中，3个位移边界条件如下：

将式（29）代入式（6）中可以得到应力的解析解：

图2和图3所示结果是利用双互易边界元法对球体进行静弹性力学分析得到的，其中图2所示为单元数量对面力相对误差的影响，图3所示为单元数量对域内应力的影响。

图2 单元数量对面力相对误差的影响曲线Fig.2 Influence curves of element number on relative error of surface force

图3 单元数量对域内应力相对误差的影响曲线Fig.3 Influence curves of element number on relative error of stress in domain

从图2和图3中可以看到，随着单元数量增多，节点数量增加，节点上各面力相对误差值和域内应力的相对误差值均随之减小，数值解均收敛于解析解，从而得到稳定面力和应力结果。这一结果说明，采用双互易边界元法分析球体的静弹性力学问题的方法是有效的。

3.2 DRBEM与FEM对比分析

本算例在实际工况下，利用DRBEM和FEM方法，对立方体模型进行静弹性力学分析，以验证实际工况下DRBEM分析结构静弹性力学方面的准确性和可行性。所用模型为边长为20 mm的立方体，笛卡尔坐标中心为立方体的质心位置，其坐标如表1所示。

表1 立方体取样点坐标Table 1 Cube sampling point coordinates

取样点位置如图4所示。立方体材料参数设置如下：密度0.007 9 t/mm3；泊松比为0.28；杨氏模量为2 000 MPa。边界条件设置如下：左表面施加压强为100 MPa；给定Z方向体力为-20 t/(s2·mm2)；下表面固定约束。

图4 正方体取样点位置分布图Fig.4 Location distribution of cube sampling points

边界元网格数量为1 608，采用非连续三角形单元类型，网格模型见图5。有限元网格数量为24 389，采用线性六面体单元类型，网格模型如图6所示。利用有限元方法仿真软件对立方体进行静力学分析，得到的位移云图如图7所示。

图5 立方体边界元网格模型Fig.5 Cube boundary element mesh model

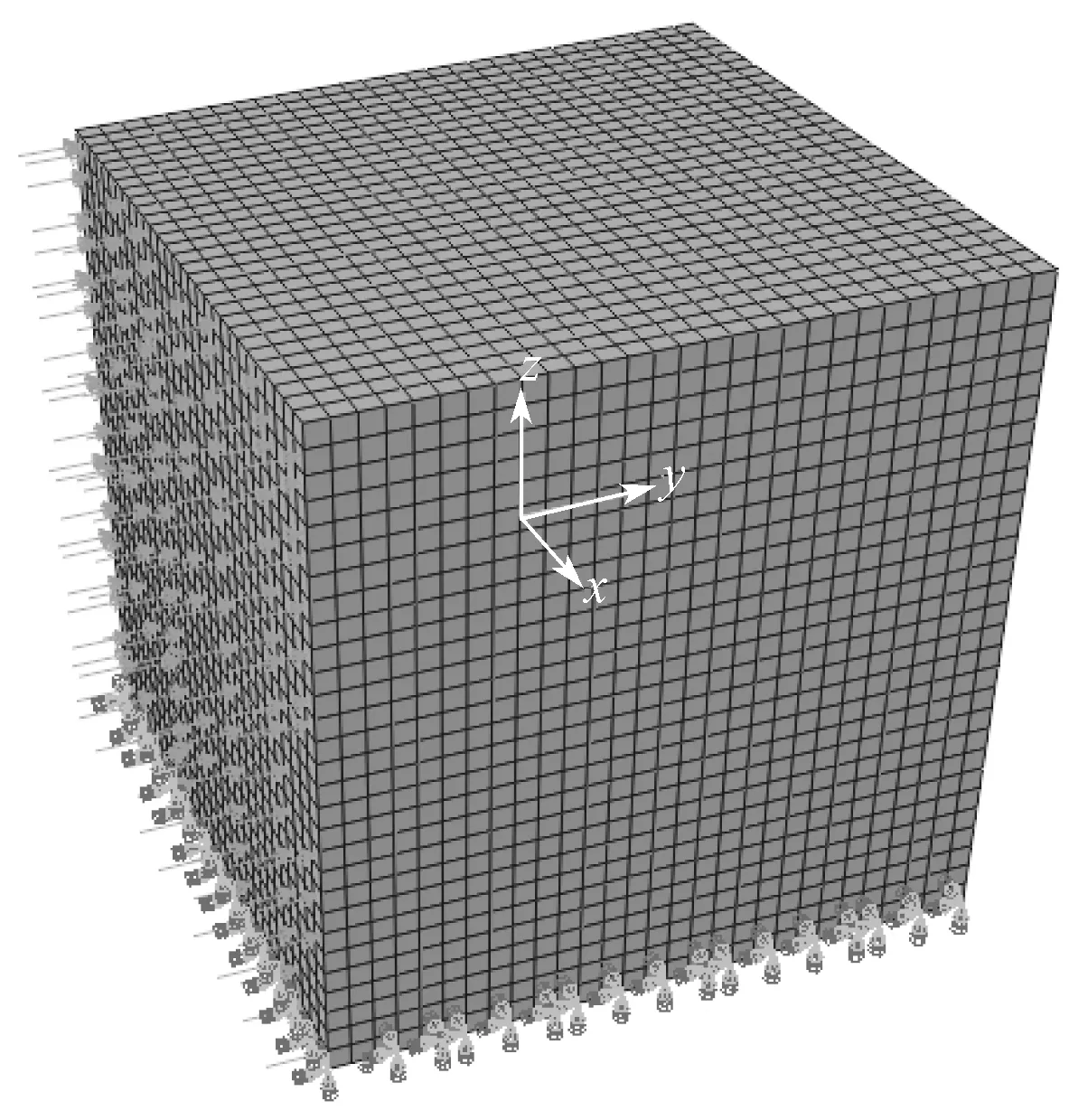
图6 立方体有限元网格模型Fig.6 Cube finite element mesh model

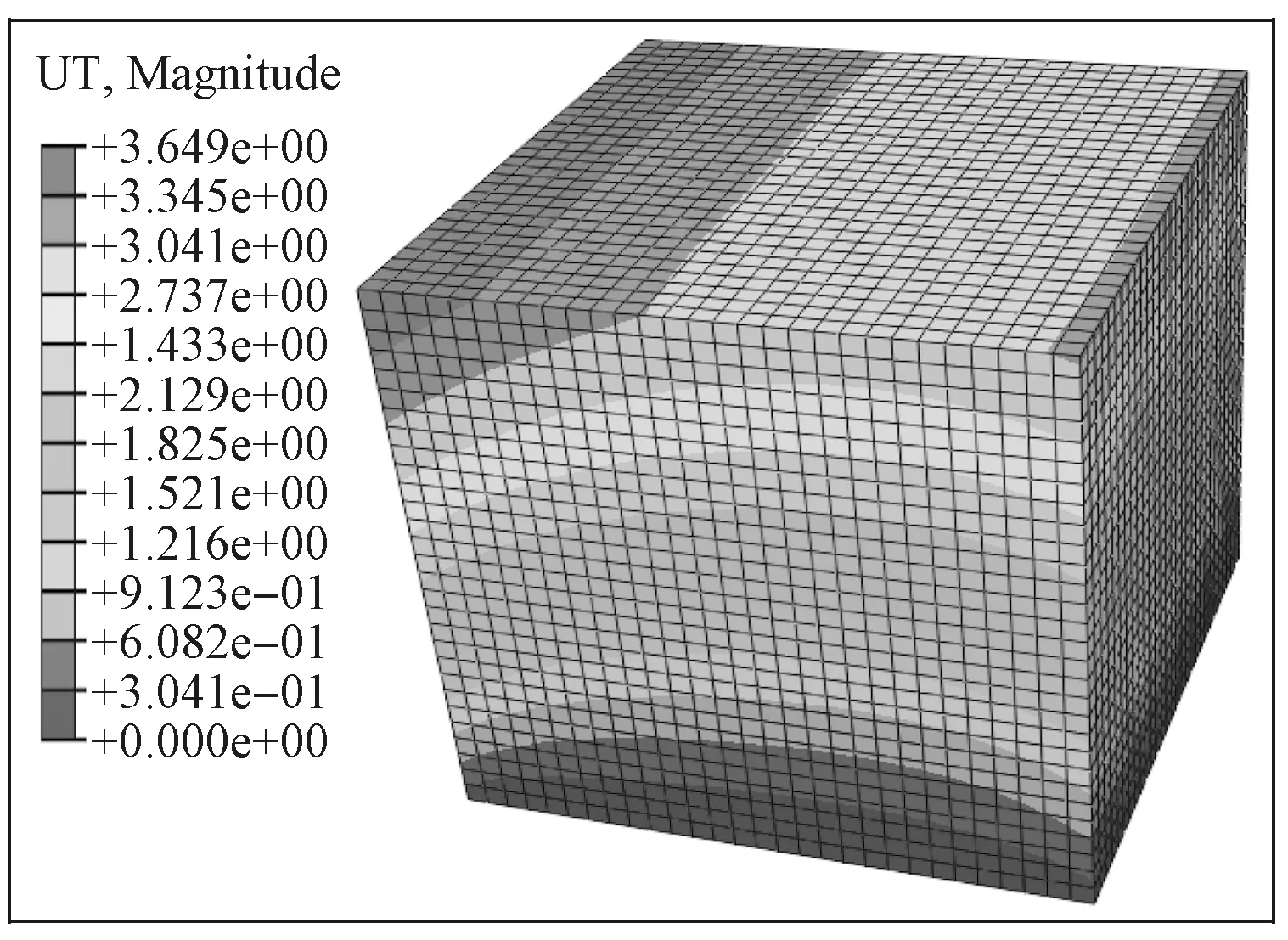
图7 有限元位移云图Fig.7 Finite element displacement nephogram of cube model

图8所示为以边界元法和有限元法的位移结果比较图，表2给出了求得的取样点的位移结果具体数据。

图8 DRBEM和FEM位移结果比较Fig.8 Comparison of displacement results between DRBEM and FEM

综合图8和表2中DRBEM和FEM的取样点位移数值情况看，两者计算位移数值结果高度拟合，该算例证明了在实际工况下双互易边界元法在分析结构静弹性力学方面的准确性和可行性。

表2 DRBEM和FEM的取样点位移结果Table 2 Displacement results of DRBEM and FEM sampling points mm

4 结语

本文介绍了双互易边界元法在静弹性力学问题中的应用，以及双互易边界元法与有限元法在静弹性力学分析中的对比。算例结果表明，双互易边界元法是分析结构静弹性力学问题的一种有效方法。在实际工况下，通过DRBEM与FEM在静弹性力学分析上的对比，进一步证明DRBEM方法在分析结构静弹性力学方面的准确性和可行性，并且具有精度高等特点。由此可见，DRBEM为分析结构静弹性力学问题提供了一种新的方法，并可以将双互易边界元法应用到解决其他领域含域积分项的非齐次问题。