正六边形蜂窝型空腹楼盖混凝土板的有效宽度计算

何嘉沛，杨晓华，何嘉杰，彭斯宁

（湖南工业大学 土木工程学院，湖南 株洲 412007）

1 研究背景

空间结构是一种较常见的结构形式，具有良好的力学性能，适用于不同跨度结构的使用要求。空腹夹层板[1]是由马克俭院士等提出并研制成功的一种新型空间结构，现已被广泛应用于大型工厂、商场、体育馆等场所。之后，混凝土空腹夹层板及U型钢板-混凝土组合空腹夹层板[2]、协同式组合空腹板等新型结构体系被广泛应用于实际工程中。但这种大跨度空腹夹层板楼盖平面网格类型比较单调[3]，只能组成正交正放[4]和正交斜放[5]等形式，适用于楼盖平面为矩形和方形的工程中。为适应大跨度建筑楼盖平面结构布置多样化，降低建造成本，有科研工作者提出了正六边形蜂窝型空腹夹层板楼盖体系[6]。近年来，国内学者针对六边形蜂窝型空间网格盒式结构楼盖进行了较多研究，并取得了一些成果。如李莉等[7]通过对蜂窝型钢筋混凝土空腹夹层板的研究，发现该结构的承载力较大，安全度较高，荷载传递、分配可靠，结构变形较小，同时验证了蜂窝型钢筋混凝土空腹夹层板楼盖结构在施工中的可行性。徐向东等[8]对六边形蜂窝型钢筋砼空腹夹层板楼盖的试验结果表明，在竖向荷载作用下，其破坏形式为弯曲破坏，且结构的塑性区域与破坏形式与实心板楼盖几乎一致。潘正斌[9]针对大跨度正六边形蜂窝型空间网格混凝土结构进行了试验研究，发现该结构具有整体性能较好、质量分布合理且竖向刚度大等特点。盛龙飞等[10]针对正六边形蜂窝型空间网格钢结构盒式结构空腹夹层板楼盖中，剪力键高度变化对楼盖整体结构刚度的影响进行了研究，发现剪力键高度的增加对提高空腹夹层板楼盖的承载能力有一定帮助，但是剪力键高度与楼盖跨度比之间存在一个限值，当超过这个限值后，楼盖整体刚度反而下降。杨彦辉等[11]利用有限元分析方法对正六边形蜂窝型空间网格大直径圆形空腹夹层板楼盖进行了静力分析，得知正六边形蜂窝状布置的空腹夹层板楼盖有三向受力特征，空间网格结构能够充分发挥钢与混凝土材料的特性，且表层钢筋混凝土板对传递楼盖竖向荷载、提高楼盖整体刚度的贡献明显。谢小华等[12]对空腹夹层板的内力计算结果与有限元模拟分析结果进行了对比研究，发现空腹钢梁材料强度对楼盖整体抗弯承载力的影响较大，而表面混凝土板的混凝土强度等级对整体抗弯承载力的影响作用较小。詹思炜等[13]通过对正六边形蜂窝型空腹夹层板进行研究后，对其各构件参数的取值给出了建议。

综上所述，正六边形蜂窝型空腹夹层板楼盖是目前空间结构研究的热点之一，但是该结构的设计计算较为复杂，有待进一步确定其简化计算模型参数。因此，本文拟利用等效刚度法，将正六边形蜂窝型空腹夹层板楼盖的表面现浇钢筋混凝土楼板，并将下部钢结构空腹梁简化为钢结构梁，然后利用有限元方法，分析正六边形蜂窝型空腹夹层板楼盖和刚度等效后的钢结构楼盖在竖向荷载作用下的静力特性，通过对比分析，研究不同混凝土楼板参与宽度的竖向挠度，计算出钢-混凝土组合结构混凝土楼板的有效宽度。并分析混凝土板有效宽度与混凝土板厚度以及钢结构空腹剪力键长细比的关系，以期为该结构的工程实际应用提供参考依据。

2 基本模型

2.1 工程概况

本研究中，正六边形蜂窝型空腹夹层板楼盖的平面尺寸如图1所示。

图1 楼盖平面尺寸Fig.1 Floor plan sizes

正六边形蜂窝型钢-混凝土空腹夹层板楼盖由上部的混凝土板与下部的钢结构梁组成[13-15]。下部钢结构梁包括T型上肋及下肋，并使用圆环形剪力键连接上肋和下肋，其剖面图见图2，正六边形蜂窝型空腹夹层板楼盖的构件参数及截面尺寸见表1。

表1 楼盖各构件参数及单元选用Table 1 Floor component parameters with their unit selection

图2 正六边形蜂窝型空腹夹层楼盖剖面图Fig.2 Sectional drawing of hexagonal honeycomb vierendeel sandwich plate floors

2.2 截面等效处理

由于正六边形蜂窝型空腹夹层板楼盖是由表面现浇钢筋混凝土板和下部钢结构空腹梁组合而成的结构，因此，忽略六边形网格连接点处钢结构剪力键的作用，根据组合结构刚度等效原则，将上表面有效宽度内的混凝土板和下部上下肋钢结构梁根据材料性能等效为均质各向同性的等高度钢截面矩形梁。上表面混凝土板有效宽度选取原则，是保证刚度等效前后整体楼盖的抗弯刚度相等。截面等效变换的目的，是为便于结构简化计算和实际工程应用，从而把研究对象等效为更利于分析的钢结构梁。

正六边形蜂窝型空腹夹层板楼盖的上肋截面尺寸为T120 mm×120 mm×8 mm×8 mm，下肋截面尺寸与上肋截面尺寸相同，截面布置与上肋反向布置，剪力键横截面为圆环，圆环外径为110 mm，厚度为8 mm，为研究剪力键高度对空腹夹层板整体抗弯刚度的影响，选取剪力键高度hj分别为280, 300,320, 340, 360 mm，等效前后的截面如图3所示。

图3 等效截面示意图Fig.3 Equivalent section diagram

上、下肋空腹钢梁截面的惯性矩I1为

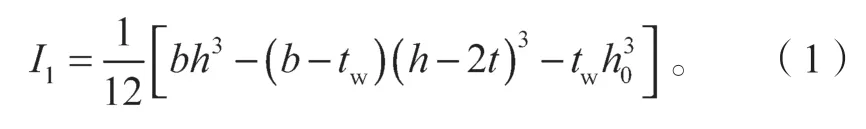
式中：b为楼盖宽度；tw为腹板厚度；t为翼缘宽度；h为截面总高度；h0为混凝土板厚度。

中性轴位置距离钢梁底面的距离yn为

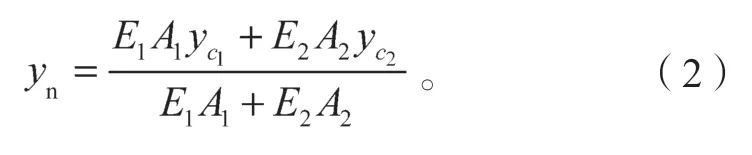
式中：E1、E2分别为混凝土与钢材的弹性模量；A1、A2分别为混凝土板有效截面面积与上下肋钢梁截面面积；、分别为混凝土板截面和上下肋钢梁截面的形心点距楼盖底面的高度。

根据等效前后刚度相等条件，可计算出等效后钢梁的截面惯性矩。

式中：I0为等效后钢梁的截面惯性矩；I2为等效前钢梁的惯性矩；h2为钢梁总高度。

3 有限元分析

3.1 模型的建立

使用ANSYS有限元结构分析软件建立有限元分析模型。钢结构空腹夹层梁T形截面上下肋和圆环截面剪力键采用BEAM188线性单元进行模拟，六边形网格每边划分为一个单元，六边形每个节点处连接上下肋的剪力键划分为一个单元。上肋共划分96个单元、下肋96个单元、剪力键28个单元，截面等效后有限元分析模型共划分220个单元。等效前有限元分析模型中，混凝土楼板采用平面壳单元SHELL181，楼盖中部均匀划分，每个网格楼板划分为36个单元，楼盖边界以及四角单元划分均适当加密，整个楼盖共划分为284个单元，等效前的有限元分析模型共划分为504个单元。计算分析时假定钢和混凝土材料均为理想各向同性弹性材料，不考虑其存在缺陷。

分析的正六边形蜂窝型大跨度空腹夹层板结构为四边简支楼盖，有限元分析时在模型楼盖周边剪力键与下肋相连处所有节点均施加X、Y、Z3个方向位移为0的边界条件，保证楼盖四周简支约束，有限元结构分析模型如图4所示。

图4 正六边形蜂窝型楼盖有限元模型Fig.4 Finite element model of hexagonal honeycomb floor

3.2 等效前的静力计算

结构分析过程中，对正六边形蜂窝型空腹夹层板结构模型施加竖向荷载，根据GB 50009—2012《建筑结构荷载规范》选择：活载为3.5 kN/m2，恒载为1.5 kN/m2，计算时施加7.5 kN/m2的竖向荷载，得到的四边简支正六边形蜂窝型空腹夹层板楼盖竖向位移云图如图5所示。

图5 四边简支正六边形蜂窝型空腹夹层板楼盖竖向位移云图Fig.5 Nephogram of vertical displacement of square simply supported hexagonal honeycomb vierendeel sandwich slab floor

由图5可以看出，四边简支正六边形蜂窝型空腹夹层板楼盖竖向位移与常规现浇混凝土梁板楼盖一样，整个楼盖的变形呈现为一个抛物面，楼盖中间的挠度最大，越靠近四周边界，挠度越小。计算得到跨中最大挠度值为20.1 mm，满足现行国家规范规定的钢混组合结构楼盖跨中最大挠度值与跨度比限值。

3.3 等效后的静力计算

结构等效原则，是将空腹夹层楼盖上表面混凝土板根据抗弯刚度不变的前提，与钢结构空腹夹层梁上翼缘一起简化为矩形钢截面。利用ANSYS有限元分析软件，建立一个没有混凝土楼板的等效空腹钢梁结构模型，等效前后楼盖厚度不变，等效后钢梁的截面如图3所示。楼面荷载根据钢梁的从属面积将其转化为等效线荷载，施加到每一根钢梁上，计算在相同荷载作用下等效结构模型的挠度。结构等效后的有限元模型如图6所示。

图6 空腹夹层板楼盖等效后的有限元模型Fig.6 Finite element model after equivalent of vierendeel sandwich plate floor

为确定空腹夹层板楼盖上表面混凝土楼板对结构抗弯刚度的影响，依据不同的楼板影响宽度，计算了多组等效后有限元结构分析模型，从而找出一个与等效前真实结构有限元模型计算得到的相同观测点挠度相近等效分析模型，这个等效模型楼盖的抗弯刚度与真实结构模型楼盖的抗弯刚度相近，其对应的楼板影响宽度即为正六边形蜂窝型空腹夹层板楼盖上表面钢筋混凝土楼板的有效宽度。等效后的竖向位移云图如图7所示。

图7 蜂窝型空腹夹层板楼盖等效后的竖向位移云图Fig.7 Nephogram of vertical displacement of honeycomb vierendeel sandwich slab floor after equivalence

3.4 长细比对有效宽度的影响

为分析剪力键刚度对表面钢筋混凝土板有效宽度的影响，在不改变剪力键直径和壁厚的情况下，通过改变剪力墙的高度来分析剪力键刚度的影响，选取剪力键高度分别为280, 300, 320, 340, 360 mm，对应剪力键长细比分别为3.75, 4.00, 4.25, 4.50, 4.80，同时分别按板厚100, 120 mm建立10组截面等效前后有限元对比分析模型，长细比的改变伴随空腹钢梁高度的改变，等同于正六边形蜂窝型空腹夹层板楼盖厚度的增加。每一组对比模型中，依据不同的楼板影响宽度，建立了多个等效后有限元结构分析模型，从而找出与等效前真实结构模型计算得到挠度值相近的等效有限元分析模型，这个等效后的有限元分析模型楼盖的抗弯刚度与真实结构模型楼盖的抗弯刚度相近，其对应的楼板宽度即为真实结构上表面钢筋混凝土楼板的有效宽度，等效前后有限元结构分析模型计算得到1点（位置如图1所示）挠度，及上表面楼板有效宽度（如表2所示）。板厚分别为100, 120 mm时，上表面钢筋混凝土楼板的有效宽度与剪力键长细比关系如图8所示。

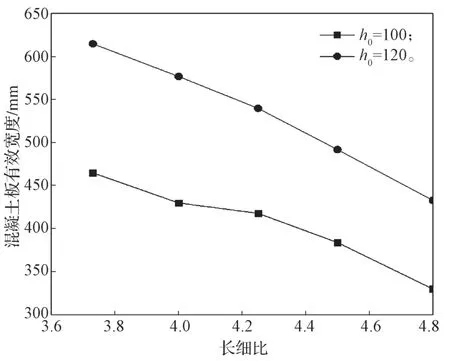
图8 长细比与有效宽度的关系曲线Fig.8 Relationship between slenderness ratio and effective width

表2 长细比与有效宽度对应值Table 2 Corresponding values of aspect ratio and effective width

从表2和图8可以得出，在不改变剪力键直径和壁厚的情况下，剪力键高度对表面钢筋混凝土楼板参与整个钢混组合楼盖的抗弯刚度范围有一定影响。在上表面楼板厚度一定的情况下，混凝土楼板参与整体结构抗弯刚度的有效宽度与剪力键高度成反比，随着剪力键高度的增加，混凝土板有效宽度逐步减小。随着剪力键高度的增加，整个楼盖厚度增加，相应楼盖整体抗弯刚度加大，竖向挠度减小。但随着剪力键高度的增加，其长细比和柔度会增加，相应剪力键自身刚度减小，使剪力键出现扭转变形且逐步增大，引起剪力键两端支承的上下肋钢梁局部变形，从而导致区格内混凝土板出现附加变形，使得参与整体结构抗弯刚度的对照混凝土板有效宽度逐步减小。

3.5 混凝土板厚度对有效宽度的影响

由表2可得出，混凝土板厚度变化直接影响楼盖整体刚度，为进一步研究混凝土板厚度变化时表面钢筋混凝土板自身厚度对其有效宽度的影响，按长细比为4.0和4.5，板厚分别为90, 100, 110, 120, 130 mm，建立10组等效前后有限元对比分析模型。表3分别给出剪力键为4.0和4.5工况下，上表面混凝土板参与空腹夹层板楼盖抗弯刚度的影响宽度。上表面混凝土板厚度对有效宽度的影响曲线如图9所示。

表3 不同长细比混凝土板厚度与有效宽度对应值Table 3 Corresponding values of concrete slab thickness and effective width with different slenderness ratios

图9 混凝土板厚度与有效宽度的关系曲线Fig.9 Relationship curves of concrete slab thickness and effective width

根据表3和图9可以得出，在剪力键高度不变的的情况下，上表面现浇混凝土采用空腹夹层板楼盖有效宽度随板厚的增加而增加，两者之间近似线性关系，这说明正六边形蜂窝型空腹夹层板楼盖抗弯刚度与上表层板厚度有关，会随混凝土板厚的增加而增大，同时挠度随板厚的增加逐渐减小。这可能是因空腹夹层板楼盖上表层混凝土板厚度增加，不但增加了整体结构的抗弯刚度，同时增加了六边形区格板的抗弯刚度，使得上表层混凝土板不易产生局部变形，故参与整体结构抗弯刚度的面积不断增加，所以增加楼板厚度会直接导致有效宽度增加。

3.6 混凝土有效宽度计算公式的拟合

为得到正六边形蜂窝型空腹夹层板楼盖上表层混凝土板有效宽度与剪力键高度，以及混凝土板厚度h0的关系曲线，将有限元结构模型分析得到的结构整合，建立3D曲面图，曲面图包含剪力键长细比和上表层混凝土厚度的影响，如图10所示。

通过图10所示曲面图的旋转观察，可以明显看到散点大致分布在一个平面上。考虑到前面的分析结果，上表层混凝土影响宽度与剪力键高度成反比，而与混凝土板厚度成正比，所以混凝土影响宽度拟合公式应是与变量板厚h0的一次线性函数，并且是与剪力键长细比的一次反比例函数，得到的拟合公式如式（4）所示。

图10 混凝土板有效宽度曲面图Fig.10 Curved surface of effective width of concrete slabs

式中：hy为上表层混凝土板采用整体结构抗弯刚度的有效宽度，其不大于正六边形网格边长的1/3；α、β为拟合系数。

图11和图12为拟合结果与有限元结构模型计算结果的对比关系图。

图11 剪力键长细比与有效宽度的关系图Fig.11 Relationship between shear bond slenderness ratio and effective width

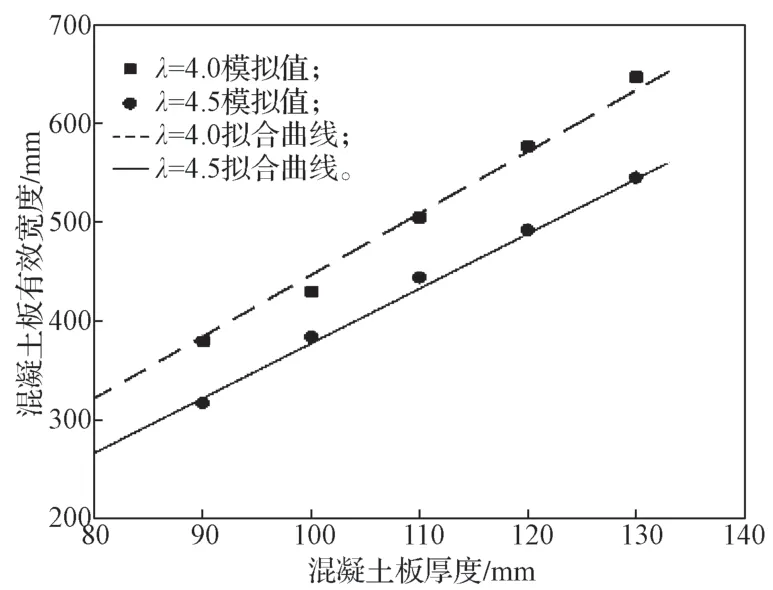
图12 混凝土板厚度与有效宽度的关系图Fig.12 Relationship between concrete slab thickness and effective width

由图11和图12可以看出，以拟合公式计算得到的结果与有限元结构模型分析结果非常相近，精确度较高，如仅考虑上表面钢筋混凝土楼板有效宽度与剪力键长细比之间关系的最大误差为5.6%，与混凝土板厚h0之间的最大误差在4.3%之内。

正六边形蜂窝型钢混组合空腹夹层板楼盖在竖向荷载作用下不但会产生整体弯曲，还因空腹梁的存在而存在区格板局部弯曲。剪力键高度和上表层混凝土板厚度都会影响其参与整体结构抗弯刚度的面积大小。相比空腹夹层梁，上表层混凝土楼板跨度较小，通常情况下板厚取100 mm左右，最小取80 mm，最大取150 mm，经计算得到上表层混凝土楼板最大有效宽度约790 mm，形成的板带边正好在六边形网格边梁与六边形形心组成的三角形形心位置附近。

4 结论

本文利用等效刚度法将正六边形蜂窝型钢混组合空腹夹层板楼盖的上表面现浇钢筋混凝土楼板和下部钢结构空腹梁简化为钢结构空腹梁，对比分析现浇混凝土楼板厚度和剪力键高度对上表层混凝土楼板参与整体结构抗弯刚度的影响宽度，建立钢-混凝土组合结构混凝土楼板有效宽度与楼板厚度以及剪力键高度的影响关系曲线，得出如下结论：

1）四边简支正六边形蜂窝型空腹夹层板楼盖竖向变形与常规现浇混凝土梁板楼盖一样，但刚度大于同等条件下的现浇混凝土梁板楼盖，楼盖的变形呈现为一个抛物面。

2）剪力键高度对上表层板参与整体结构抗弯刚度的影响较大，两者之间呈反比关系，在不改变剪力键直径和壁厚的情况下，剪力键高度的增加，现浇混凝土板有效影响宽度减小，故剪力键高度不宜过大。

3）正六边形蜂窝型钢混组合空腹夹层板楼盖，在竖向荷载作用下不但会产生整体弯曲，还存在区格板的局部弯曲。加大上表层混凝土板厚度会提高楼板抵抗区格内局部弯曲能力，上表面混凝土板参与整体结构抗弯刚度的面积随之加大，所以随着混凝土板厚度增加，其有效宽度逐渐增加，近似为线性变化。