一类分数阶食饵-捕食者系统的动力学分析
张学友,赵 薇,赵育林
(湖南工业大学 理学院,湖南 株洲 412007)
0 引言
食饵-捕食者关系是自然界中普遍存在的一种物种间相互作用的基本关系,相关学者建立了大量的生物种群模型来揭示具有不同功能反应的食饵-捕食者相互作用关系。因此,探讨生物种群系统的运行规律以及人类对生态系统的开发利用策略,具有十分重要的意义和实践价值[1-3]。同时,随着种群生态动力学以及分数阶微分方程理论的发展,分数阶生物微分系统的研究已成为当前生物数学研究领域中的热点之一,许多学者对此做了大量的研究工作[4-10]。本文在已讨论的两种群整数阶生物模型的基础上,研究如下一类食饵具有密度制约和避难所的Holling-II型分数阶食饵-捕食者系统:

式中:x为食饵的种群密度;
y为捕食者的种群密度;
a为食饵的内禀增长率;
b为食饵的密度制约系数;
c为捕食种群的捕食强度;
d为捕食者的死亡率;
e为营养转化率;
p为捕食者的处理时间;
r为食饵的增长率;
t为时间;
θ为捕食者的捕获率;
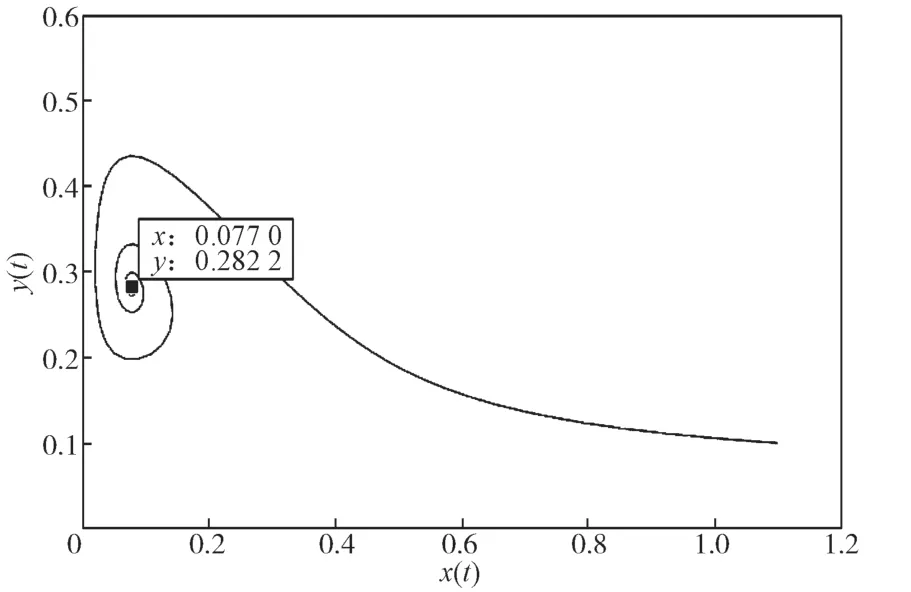
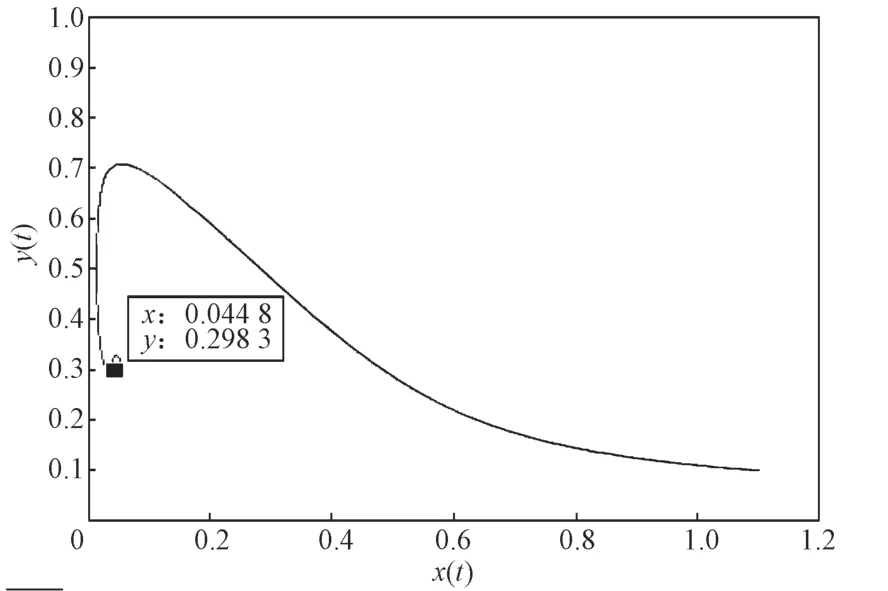
m为在避难所中的食饵种群的比例,0 mx为避难所保护的食饵数量; (1-m)x为捕食者能捕获的食饵数量; 本文在各参数满足一定条件下,讨论系统(1)解的存在唯一性、非负性、有界性以及平衡点的稳定性等问题,同时利用Matlab软件进行数值仿真检验。 定义1[9]设β>0,函数f(t)定义在区间[a, +∞)上n阶可导,则函数f(t)的β阶Caputo分数阶导数定义为 其中n=[β]+1,n-1<β≤n,[β]表示β的整数部分;Γ(·)为Gamma函数。 引理1[7,10]设系统 其中Eβ是Mittag-Leffler函数,即 其中 因此 定理2系统(1)的所有解都是非负的,对于任意的初值条件都成立,其中 证明要证系统(1)的解的非负性,即证对任意t≥0都有x(t)≥0。 显然t=0时,x(0)>0。 下证当t>0时,有x(t)≥0。 假设存在t1>0使得x(t1)<0,由x(t)的连续性和x(0)>0,则,使得x(t2)=0。记t3=min{t2>0:x(t2)=0},则当t=t3时,有 此外,由t3的定义以及x(0)>0可得,当时,有x(t)≥0。 令z(t)=-x(t),,则z(t3)=0且z(t)<0,。 类似地,可以证明,对任意t≥0都有y(t)≥0。定理2得证。 定理3集合 是系统(1)的一个正不变集。 证明构造函数W(t)=ex(t)+y(t),于是有 则有 由W(0)=ex(0)+y(0)>0,根据引理2可得 由引理4可得,系统(1)从A中的一个点出发的解,永远保留在A中,所以集合A是系统(1)的一个正不变集。定理3得证。 定理4集合 证明由定理3可知,对于任意给定的初始条件,若是满足,则系统(1)的解总包含在集合A中。 由引理4可得,系统(1)的全部解都收敛于集合A。进一步可以得出集合A是一个全局吸引集。显然,A同时也是一个有界集,因此系统(1)的全部解是有界的。定理4得证。 通过计算,可求得系统(1)对应的Jacobi矩阵 证明在平衡点处,系统(1)的Jacobi矩阵为 其特征方程为 解得其特征根为 其特征方程为 其中 所以系统的特征根可表示为 从而得到以下结论。 定理7如果系统(1)满足下列条件之一: 那么系统(1)的正平衡点P2是局部渐进稳定的。 证明当条件1)满足时,显然λ1<0,λ2<0,从而有 由引理5可得,正平衡点P2是局部渐进稳定的。 当条件2)满足时,λ1与λ2是一对共轭复根,且Re(λ1)=Re(λ2)<0,Im(λ1)=-Im(λ2)>0。可求得 由引理5可得,正平衡点P2是局部渐进稳定的。 当条件3)满足时,λ1与λ2是一对共轭复根,且Re(λ1)=Re(λ2)>0,Im(λ1)=-Im(λ2)>0。可求得 由引理5可得,正平衡点P2是局部渐进稳定的。 由引理6可得,正平衡点是局部渐进稳定的。 定理8如果系统(1)满足下列条件之一: 那么系统(1)的正平衡点P2是鞍点。 证明当条件1)满足时,有λ1>0、λ2<0,则有 由引理6可得,平衡点P2是鞍点。 当条件2)满足时,显然λ1>0、λ2<0 ,则有 由引理6可得,正平衡点P2是鞍点。 当条件3)满足时,显然λ1>0、λ2<0,则有 由引理6可得,正平衡点P2是鞍点。 定理9当时,如果系统(1)满足下列条件之一: 那么系统(1)的正平衡点P2是不稳定的。 证明当条件1)满足时,显然λ1>0、λ2>0,则因此系统(1)的正平衡点P2是不稳定的。 当条件2)满足时,λ1与λ是一对共轭复根,且Re(λ1)=Re(λ2)>0,Im(λ1)=-Im(λ2)>0,可求得 因此系统(1)的正平衡点P2是不稳定的。 用Matlab进行数值仿真,以验证本研究所得结论的正确性。 对系统(1)的参数赋值如下:r=2.5,a=0.5,b=1,c=0.2,d=0.15,e=0.6,θ=3.5,p=1。 系统(1)在点P2=(0.077 0, 0.282 2)处的仿真结果如图1所示。由图可知,正平衡点P2=(0.077 0, 0.282 2)是局部渐进稳定的,与理论结果一致。 图1 系统(1)在点P2=(0.077 0, 0.282 2)处的仿真结果Fig.1 Simulation results of system (1) with point P2=(0.077 0, 0.282 2) 2)当β=0.95,食饵无避难所(m=0)的分数阶种群模型。通过计算可得正平衡点P2=(0.044 8,0.298 3),同时可得,,。由定理7得,正平衡点P2=(0.044 8, 0.298 3)是局部渐进稳定的。 系统(1)在点P2=(0.044 8, 0.298 3)处的仿真结果如图2所示。由图可知,正平衡点P2=(0.044 8, 0.298 3)是局部渐进稳定的,与理论结果一致。 图2 系统(1)在点P2=(0.044 8, 0.298 3)处的仿真结果Fig.2 Simulation results of system (1) with point P2=(0.044 8, 0.298 3) 3)当β=0.95,m=0.6的分数阶有避难所食饵具有密度制约的Holling-II型功能反应函数模型。通过计算可得正平衡点P2=(0.085 6, 0.304 0),,而且,,。由定理7得,正平衡点P2=(0.085 6, 0.304 0)是局部渐进稳定的。 系统(1)在点P2=(0.085 6, 0.304 0)处的仿真结果如图3所示。由图可知,正平衡点P2=(0.085 6, 0.304 0)是局部渐进稳定的,与理论结果一致。 图3 系统(1)在点P2=(0.085 6, 0.304 0)处的仿真结果Fig.3 Simulation results of system (1) with point P2=(0.085 6, 0.304 0) 4)当β=0.95,m=0.6时,由定理5可知,系统(1)的平衡点P0=(0, 0)是鞍点。系统(1)在点P0=(0, 0)处的仿真结果如图4所示。由图可知,平衡点P0=(0, 0)是鞍点,与理论结果一致。 图4 系统(1)在点P0=(0, 0)处的仿真结果Fig.4 Simulation results of point P0=(0, 0) for system (1) 本文研究了一类食饵具有密度制约和避难所的Holling-II型分数阶食饵-捕食者系统的动力学性质,讨论了系统解的存在唯一性、非负性和有界性,分析了平衡点存在的条件以及各类平衡点的局部渐进稳定性,并通过数值仿真验证了有关结论的正确性。 数值仿真结果表明:分数阶种群模型比整数阶种群模型能更快达到稳定,有避难所种群模型比无避难所种群模型能更快达到稳定。食饵具有避难所的分数阶种群模型,比单独具有其中之一的种群模型能够更迅速地达到稳定。1 预备知识
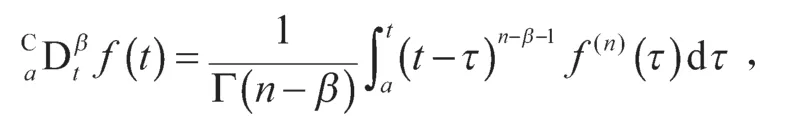
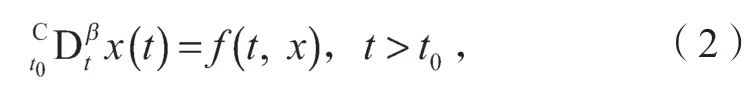

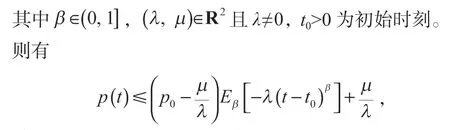

2 系统动力学分析
2.1 解的存在唯一性、非负性和有界性

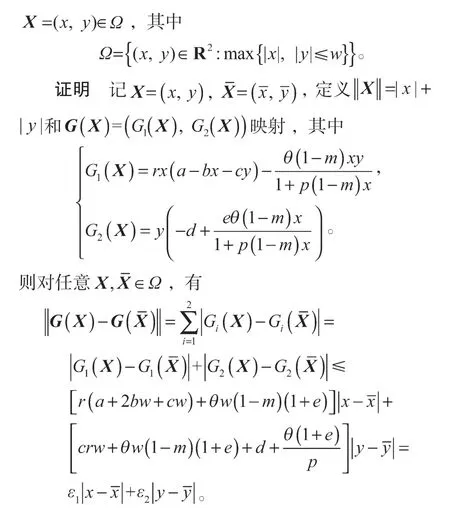


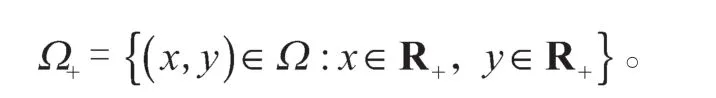

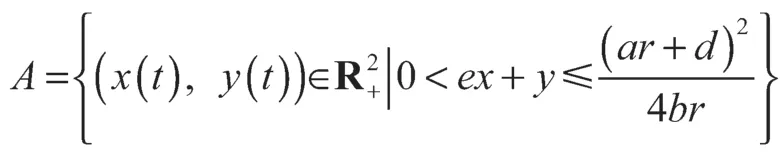





2.2 平衡点的局部稳定性












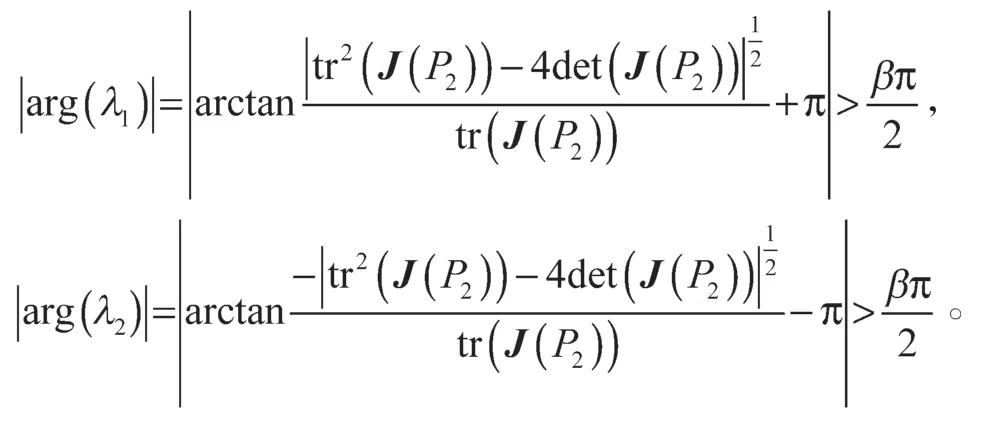




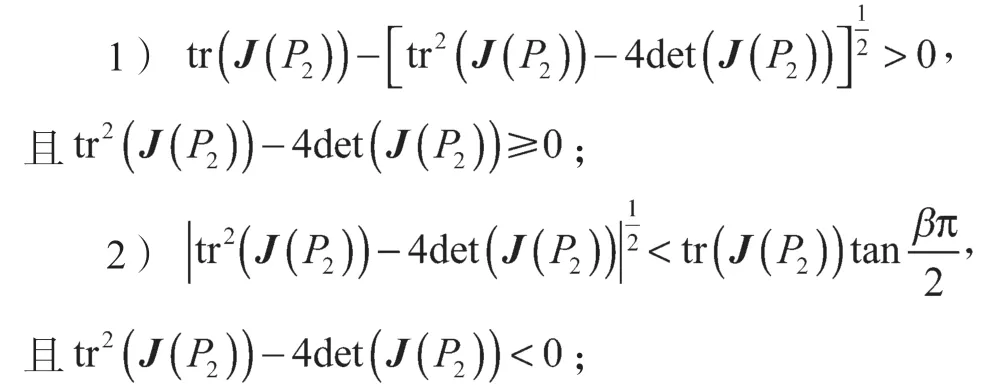

3 数值仿真



4 结语

