聚焦计算本质，提高学生的运算能力

蒋杏芬

【摘要】計算是小学数学教学的基本要素和重要内容。学生良好的运算能力，是今后学生生活学习和社会活动所必备的基本素养之一。所以，培养学生的运算能力是小学数学课堂教学的一项重要任务。《义务教育数学课程标准（2011年版）》中指出：人人都要获得必要的数学素养以及必要的运算能力。然而，当前部分老师在计算课堂教学中对计算教学的核心内容和知识本质把握不到位，存在重算法轻算理，重结果轻过程，重技能轻思维的教学现象，学生运算能力得不到真正的提高，数学思维能力也得不到更好的发展。在此，笔者对如何通过聚焦计算的本质和内涵提高学生的运算能力，谈谈个人的一些浅见。

【关键词】小学数学;计算;本质;运算能力

引言

计算的本质在于对算理的推理过程中形成算法。算理是计算的思维本质，也是计算的理论依据，其内涵包括数和运算的意义、运算规律和性质，主要解决“为什么这样算”的问题。“算法”是”算理”的外在表达形式，是避开了复杂思维过程的程式化的操作步骤。 计算教学中，学生运算能力的培养需要经历数学抽象、数学推理、数学建模的有效探究和学习过程。所以，要使学生在学习活动中真正理解算理，准确掌握算法，主动构建知识模型，提高运算的数学思维能力，需要老师挖掘计算的本源，把握知识的本质，精心组织教学活动，让学生真正经历计算推理到算法形成的思维过程。

一、 源头中温故知新 ，感知知识本源

任何新知识的学习都是建立在原有知识和生活经验的基础上进行的，数学学习也不例外。所以，找准新旧知识的切入点就是找到了走进新知的钥匙，找到计算教学新知所含算理的源头活水，就能敲开了学生学习新知的思维大门。例如人教版五年级上册“除数是小数的小数除法”一课，是在学生已经掌握“商不变的性质”和“除数是整数的小数除法”的基础上进行教学的。学生对除数是整数的除法的算理及商的小数点的定位方法刚在前两课时学过，尚记忆犹新，而“商不变的性质”学习时间相隔有一年，对具体的变化规律似乎早已淡忘，所以这一课利用“商不变的性质”将除数是小数的除法转化为除数是整数进行计算对学生来说是一个重点，也是一个难点。所以要突破本节课“如何转化？”的重难点问题，在复习导入时就非常有必要设计了一道“商不变的规律”练习题进行旧知导入，如采用表格的形式设置了三组数据：

让学生计算出每组数据的商都是0.3，再观察每两组数之间的变化规律，从而有效的引起了学生对“商不变的性质”的回忆，温故而知新，激发学生的求知欲，为接下来除数是小数的小数除法的学习做了很好的铺垫，给学生的思维搭上一座连接新知的桥梁，让学生找到算理的源头活水，感悟“商不变的性质”是“除数是小数的小数除法”的计算本源。

二、操作中明理得法，聚焦计算本质

我们知道计算是枯燥的，如果没有一定的运算原理做支撑，法则的框架最终会支离破碎。算理难懂，不知道如何去引导学生理解算法背后的算理？是我们大部分教师目前比较困惑的问题。心理学家皮亚杰认为：“儿童的思维是从动作开始的，切断了动作和思维之间的联系，思维就得不到发展。”苏霍姆林斯基曾说过：“智慧在手指上”。学生在操作中能感知大量直观形象的事物，获得感性知识，形成知识的表象，从事物的表象中概括出事物的本质特征，从而形成科学的概念或法则。因以，引导学生进行具体、直观的操作推理，可以让学生真正地理解算法背后的道理。如实物、摆小棒、圈点子图、借助学具等操作，可以很好地帮助学生在不同表征的转化推理过程中理解算理，形成抽象的算法。例如人教版三年级上册“多位数乘一位数（一次进位）的笔算乘法”，在出示王老师在书店购买连环画的主题图后引导学生通过“摆小棒”的直观操作，让学生经历算理直观到算法抽象的推理过程，明白“16×3=48”算法背后的算理所在，使学生知其然并知其所以然。

（一）动手操作，理解算理

操作一：

问1：仔细观察这幅图（主题图），你知道了哪些数学信息？

问2：“每套16本”怎么摆？

这里先引导学生弄明白“16里面有几个十和几个一？”

再由学生演示摆小棒。

追问3：第二套又怎么摆？

第三套呢？

问4：你会摆吗？台下同桌一起摆摆看。（每个学生都动手摆起来）

通过第一阶段的操作，形成直观的、结构性的小棒图，为接下来的算理理解提供直观形象的思维模型。

操作二：

提出问题列出算式后：

问1：16×3的结果是多少呢？可以通过摆好的小棒图计算出来吗？同时记录：

6×3=18

10×3=30

18+30=48

追问2：小棒图的左边明明只有“3个十”，结果（48）这里为什么却有“4个十”呢？

学生看图回答并操作“捆小棒”：小棒图的右边一共有18根小棒，也就是“1个十”和“8个一”根，这里的“1个十”又可以捆成一捆，还剩“8个一”，所以结果是“4个十”和“8个一”，也就是48根。

第二阶段的“捆小棒”操作，为学生在“多位数乘一位数（一次进位）的笔算乘法”中的“满十进一”算理难理解的问题上，提供了直观的理论依据，让学生在一步步的操作推理中明理，为算理到算法的过渡，搭建好了桥梁。“纸上得来终觉浅，绝知此事须躬行”。为此，我们必须倡导数学学习的实践性，在体验中学习，在探究推理中寻得计算的本质，通过动手操作使之再学习、再创造，这不失之为提高学生运算能力，培养学生数学思维的好方法。

（二）数形结合 ，形成算法

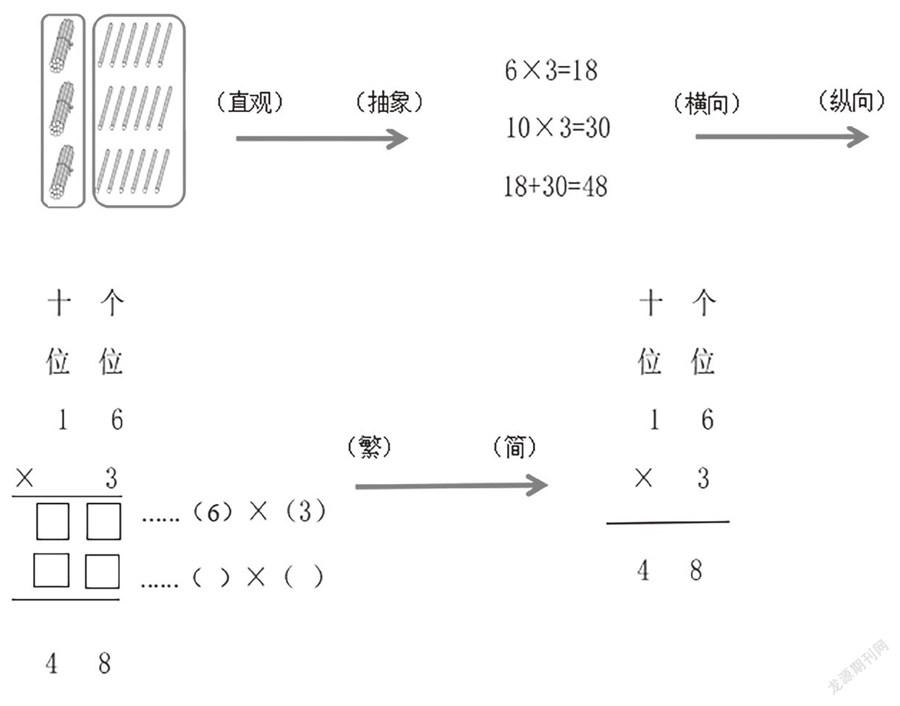
直观的算理是支撑算法形成的依据。算法的形成需要以操作中形成的直观性、结构性或逻辑性的模型为依托，进行多元表征之间的完美转化，最后进行类比、归纳、总结，从而形成具体、明晰、简洁的计算法则。 这里还是以“多位数乘一位数（一次进位）的笔算乘法”为例， 通过以下的推理和转换过程来实现“明理得法”。

学生在以上探究学习过程中，经历了直观图形到数学符号的转化、横向算式到纵向算式的转化，再是数学符号由繁到简的转化，学生从形象思维到抽象思维的形成，从感性认识到理性认识的升华，整个教学活动紧紧围绕计算的本质——计算原理的推理过程，使学生在不断的推理、转化中掌握笔算的程序和步骤，同时理解程序和步骤背后的道理所在。

三、类比中构建模型，突显计算内涵

数学建模是对实际问题进行的数学抽象。计算教学中运算法则的构建常常可以通过新旧知识之间的类比迁移来实现。采取类比推理的方法促使学生回顾旧知，在已有知识的基础上去发现新结论、构建新知识，可以有效地实现旧知识在新内容中的正迁移，帮助学生突破教学难点，建立新的计算法则。例如：构建“多位数乘一位数（一次进位）的笔算乘法”的算法时，可以通过已有知识“43×2”不进位的算法与“16×3”一次进位的算法进行比较，找出它们算法上的共同点和不同点，再通过“16×3”与“152×4”进位上不相同的比较，推理出“满几十就向前进几”的知识内涵，引导学生构建出“多位数乘一位数（一次进位）的笔算乘法”新的数学计算模型，促进学生数学思维能力的发展。

四、应用中知能内化，提升运算能力

学以致用，是检验学生学习效果的关键一环。学生运算能力的进一步提高，取决于知能应用练习题组的设计是否做到夯实基础，发展思维。所以，在巩固应用环节中，运算不能只停留在技能的巩固，更要重视能力的培养。一是找准重点，夯实基础。根据基本的计算方法，把基本习题变换提问的角度，或者是提问的形式，如计算、选择、填空等，以各种“变式题”促使学生从更多的角度去观察、理解、巩固所学的知识。二是抓住难点，强化思维 。例如学完除数是小数的除法后，可以抓住学生思维认识中仍存在的“瓶颈”“障碍”，呈现学生在计算中出现的易错题，让学生当“啄木鸟医生”：指出这些计算错在哪里？为什么会出这样的错误？应该注意什么问题等。让学生做一回当医生找毛病的瘾，“治愈”学生知识中存在的问题，夯实计算技能的同时提升运算的灵活性。学完小数除法后，还可以安排学生计算“被除数比除数小数位多”的类型“0.544÷0.16 ”这是例题中没有出现的类型，增加这类题的计算训练，既弥补薄弱，又能突破难点。三是内化算法，提升能力。教材中有不少练习，如果仅仅以“算得又对又快”为目的，则其运算意识与能力培养将大打折扣。所以，一方面要善于挖掘习题内涵，捕捉巩固训练中能力培养的契机，另一方面则需要精心设计，选择发散性思维的问题进行训练。让学生知道该怎样算，思考并解决为什么这样算，还可以怎样算， 等一系列的问题。通过从不同侧面的练习训练来揭示知识的本质，加深学生对知识的理解和運用的水平，进一步提升学生的运算能力。

结语

核心素养下小学生运算能力的提高，离不开对计算本质和内涵的探究和学习， 学生“明理得法”的学习过程，则要求教师对计算教学知识本质的准确把握和理解，并转化成有效的教学行为。因此，作为教师既要了解学生的学习起点，挖掘教材中的知识本质和核心内容，也要关注学生学习过程中思维能力的培养，把计算教学聚焦在：引导学生充分经历“明理得法”计算推理的过程，使计算与推理同步，推理与思维统一 ，逐步提高学生运算的思维水平和能力。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

[2] 张洪霞.小学数学计算教学策略研究[D].东北师范大学，2012.

[3]戴曙光.简单教数学[M].上海：华东师范大学出版社， 2012，8.

[4]吴正宪，周卫红，陈凤伟.吴正宪课堂教学策略[M]. 上海：华东师范大学出版社，2012，8.

（责任编辑：伍静仪）