一种新的监测往复压缩机活塞杆下沉量的模型算法

刘 江，张恩贵，杨清华

(中国石油四川石化设备检修部，四川 彭州 611930)

1 引言

往复压缩机结构复杂、易损件多，故障率一直居高不下，尤其支撑环活塞环磨损、活塞拉缸、十字头抱死等故障也并未得到有效遏制。因此，获取关键信息数据，建立科学有效的计算模型，精准预测失效位置及严重程度，对机组长周期安全运行至关重要。

笔者在前人研究成果的基础上，结合多年实践研究，对目前行业普遍采用的活塞杆沉降计算模型进行优化，并在工程实践中得到验证。

2 目前行业计算模型

至今国内外大多数大型往复压缩机活塞杆上部或下部加装了电涡流传感器，来监测数据变化，已有很多专家学者对机组故障特征提取做了大量的研究工作，并在实践中得到广泛应用。

美国石油协会在2007年颁发的API618[1]标准6.3.1和C.3.3中明确提到“卧室往复压缩机活塞杆水平和垂直冷态径向跳动偏差范围在行程的±0.015%之内”“盘车试验刻度盘指示器活塞杆水平(侧向)径向跳动不应超过0.064 mm，不考虑行程长度”“考虑到可能造成轻微平行偏移或角偏差的所有零件的几何和配合公差，加上或减去行程许用限值的±0.015%”。同时，该标准中图C-4对活塞杆重力产生的挠度在千分表处的几何变形进行了专利计算；标准中C.4.5还提到“在正确对中条件下并无活塞杆下沉，垂直活塞杆径向跳动非常接近一个成比例的直角三角形关系”，其公式如下。

该模型公式未考虑十字头滑履磨损，因此与实际情况存在一定偏差。

同时，文献[2]还介绍了第二种计算活塞支撑环磨损的物理模型及方法(图1)，也在行业中广泛应用。

但实践研究表明，由于该方法考虑的要素较少，模型未考虑十字头滑履磨损，未考虑拉缸时支撑环临界磨损余量，在确定L1、L2时也未明确活塞的具体位置，因此测算A值与实际检修偏差较大，只能简易计算支撑环磨损的大致情况。

计算模型如下：首先测量十字头和支撑环到传感器的长度L1、L2，通过电涡流传感器测量活塞杆下沉数值B，通过相似三角形原理，计算公式如下

(1)

计算得到支撑环实际磨损量

(2)

3 计算模型改进

基于上述模型，在不考虑活塞杆重力产生的挠曲变形和十字头垂直方向的交变载荷对活塞杆的影响，假设活塞杆绝对水平，以传感器与活塞杆的相对运动，确定远死点和近死点的具体位置，考虑拉缸时支撑环临界磨损余量，将L3延长至活塞端面，重新确定了L1、L2、L3的长度，建立图2所示的计算模型。通过状态监测系统的电涡流传感器采集活塞杆全行程的运动间隙，形成360°活塞杆沉降波形，根据监测数据提取特征值。

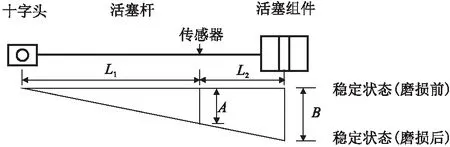
图1 目前往复压缩机支撑环磨损计算模型

特征值1：下沉量，取其运动间隙波形的平均值，即信号直流量y。

(3)

特征值2：波动量，取其运动间隙波形的峰峰值，即信号交流量p。

p=-Xa+Xb

(4)

4 计算方法及步骤

鉴于初始状态非理想水平状态，一般存在倾斜，因此将磨损前的稳定状态1定义为磨损前初始状态，将磨损后的稳定状态2定义为磨损后稳定状态，考虑十字头滑履磨损对特征值的影响，建立图3所示计算模型。

4.1 计算ΔXa和ΔXb

针对活塞杆磨损前后的稳定状态，列出其特征值，推导求解电涡流传感器在远死点、近死点的变化量ΔXa和ΔXb。

图2 改进后的往复压缩机支撑环磨损计算模型(理想状态下)

图3 改进后的往复压缩机支撑环磨损计算模型(实际状态下)

稳定状态1的特征值

(5)

p1=-Xa+Xb

(6)

稳定状态2的特征值

(7)

p2=-Xa-ΔXa+Xb+ΔXb

(8)

联合公式(5)～(8)推导出

(9)

p2-p1=-ΔXa+ΔXb

(10)

联合公式(9)、(10)求解出

(11)

(12)

4.2 计算ΔXi和ΔXj

参照相似三角形原理，列出比例恒等式，推导求解出十字头滑履、活塞支撑环的变化量ΔXi和ΔXj。

(13)

(14)

联合公式(11)～(14)求解出

(15)

(16)

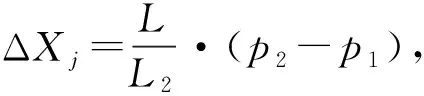
5 结语

笔者采用该计算模型对22台往复压缩机运行情况进行实时监测，已先后发现了十字头滑履磨损、十字头销报死、支撑环和活塞环磨损等30余起故障，不仅提高了支撑环磨损的计算精度，而且还能及时发现了十字头存在的问题，在工程实践中得到充分验证，期望该技术能在行业中得到推广应用。