考虑相界面对压力波传播影响的汽车空调管路气流脉动研究

吴伟烽，李程翊，张 寅，李晓然

(西安交通大学能源与动力工程学院，陕西 西安 710049)

1 引言

近年来，随着家用轿车的逐渐普及和电动汽车技术的快速发展，人们对轿车的舒适性有了更高的要求。与传统内燃机相比，新能源汽车电动机的振动及噪声较小，空调系统的振动及噪声成为了影响汽车NVH(Noise，Vibration，Harshness)性能的主要因素[1，2]。目前市场上汽车空调压缩机以斜盘式为主流机型。斜盘式压缩机间歇性地吸排气的工作特点引起了空调系统内制冷剂流量与压力的周期性脉动，成为空调系统管路振动及噪声的主要激励源。因此汽车空调压缩机排气压力脉动规律的研究，成为了改善其NVH性能的关键一步。

本文采用平面波动理论常用于空气压缩机系统气流脉动的计算。近年来，利用计算流体力学的方法研究气流脉动逐渐兴起，并被指出更具准确性[3-5]。张振乾利用平面波动理论，推导出复杂压缩机管网系统的传递矩阵，使用ANSYS声学模态分析的方法验证了传递矩阵的精确性[6]。徐斌采用有限振幅法模拟计算了空气压缩机管道的大振幅气流脉动，并实验验证了该方法的准确性[7]。Zhan Liu等人基于线性声波理论和传递矩阵法，计算了装有横流穿孔管的压缩机管道系统气流脉动，与实验结果的偏差不超过6.8%[8]。在空调系统气流脉动研究方面，Jeong Il Park及Douglas E.Adams结合压缩机热力模型、气阀模型及活塞动力学模型改进了传递矩阵方法，并搭建空调系统实验台验证了该方法的精确性[9]。徐傲使用LMS.Virtual.1ab和FLUENT软件，采用有限元方法计算了不同结构下管路进出口压力损失，分析了管路连接方式对管路整体声学性能的影响[10]。

对于汽车空调系统压力脉动及振动噪声的研究，使用最为广泛的方法仍是传递矩阵法以及有限元法。侯艳芳[11]测量了空调系统的噪声，发现频率为500～750 Hz的吸气脉动和排气脉动噪声是主要噪声来源。Seong-Hyeon Lee[12]通过实验与数值模拟对机械力与脉动压力进行了分析，测量了管道系统中多个点的振动，验证了模拟结果。刘华，陈文卿等对变频双螺杆制冷压缩机气流脉动衰减器进行了试验研究，加装了一种宽频带孔板的气流脉动衰减器，并分析了压缩机运行转速对其衰减性能的影响，有效地解决变频双螺杆压缩机气流脉动诱发的排气噪声问题[13]。王翔做了改善汽车空调中斜盘式变排量压缩机吸排气脉动情况的研究，结果表明在吸排气气路增加单向阀和使阀板密封带变窄可组合使用以提升噪声抑制效果[14]。Xiaokun Wu，Ziwen Xing等人基于Helmholtz谐振器理论，提出了一种应用于双螺杆制冷压缩机排气腔的脉动阻尼器(PPD)，建立了制冷剂-油混合物模型与压力脉动仿真模型相结合的数学模型，实验和模拟对比结果表明，在250 Hz的设计频率下，安装了PPD的系统振动加速度降低了36.2%至41.1%[15]。

目前行业对汽车空调气流脉动规律的研究，大多仍采用传统的转移矩阵法，但该方法对于相变系统的适用性和求解精度差。为此，本文针对汽车空调系统存在相变的特点，利用平面波动理论并考虑气液相界面对压力波传播的影响，建立了压力波动方程，求解结果给空调系统的管路设计提供了参考依据。

2 平面波动理论

汽车空调系统产生的振动及噪声主要有两大来源：一是气流脉动引起的气柱系统振动；二是机械振动。机械振动源头易发现、振动幅度易衰减，而气流脉动引起的振动却难以消除，是现阶段制冷系统振动及噪声研究最受关注的部分。汽车空调斜盘式压缩机的气缸组件的基本结构，如图1所示，它主要由控制气体流动的吸气阀、排气阀、气缸、活塞、驱动活塞的斜盘主轴及其它辅助元件组成。汽车动力系统通过皮带控制斜盘主轴转动，从而带动嵌套在斜盘的活塞作往复运动，在工作腔内形成了进气、压缩、排气和膨胀的循环过程，即实现了压缩机的一个工作循环。

图1 斜盘式压缩机气缸组件[16]

由于容积式压缩机间歇性吸、排气的工作特点，导致制冷系统内的制冷剂流动呈现为周期性非定常流动。在压缩机的一个工作周期内，排气阀多数时间处于关闭状态，当腔室内的压力达到规定值时，排气阀突然打开，气体冲出气缸及排气腔。具有可压缩性的制冷剂气体可看作一个具有连续质量的弹性振动系统，会因扰动产生相应的振动。从气缸排出的气流撞击管道中原本存在的气体，成为使整个系统产生脉动的扰动源。扰动在系统管路内以声波的形式传播，其传播、反射、透射等使得管内各处制冷剂的状态不断变化，这就是汽车空调系统内的气流脉动。

声波是纵波，能改变管路轴向控制体积中制冷剂分子的分布，使其呈现疏密相间的状态，分子团密集的地方压力高，分子团稀疏的地方压力低[17]。实际上，声波的传播就是制冷系统内中制冷剂分子空间分布疏密变化的交替过程。系统内声波的传播造成了制冷剂的压力脉动，因此建立声波的波动方程是解决气流脉动问题的第一步。此外，由于制冷系统内存在相变，在换热器前后的管路内存在气液相界面。本文基于平面波动理论，在考虑换热器相变界面对压力波的影响，研究制冷系统管道内的压力波动。采用平面波动理论计算气流脉动时，需要满足以下假设：

(1)汽车空调系统制冷剂管路的内径远小于其长度，声波仅沿管道轴向传播。

(2)制冷剂粘度对流动的阻尼作用较小，且压力波在制冷剂气体中的传播没有能量耗散。

(3)相较于汽车空调系统中高压气体的压力时均值，气体压力脉动值处于一个较小的范围，即各项声压脉动量远小于流体流动过程中的平均值。特别地，由于声波扰动造成的密度的改变忽略不计。

(1)

式中p0——工质压力的脉动值，Pa

u0——工质速度的脉动值，m/s

ρ0——工质密度的脉动值，kg/m3

p*，u*，ρ*——相应的时均值

a——声速，即扰动传播的速度，m/s

(4)流动过程是绝热的，即气体不与管道外部进行热交换，且纵波引起的局部分子簇稀疏或致密变化的过程无热量交换。

前2条假设说明，气体分子簇的振动在管路径向上具有一致的振幅和相位，波阵面是平面，所以这种方法也称为平面波动理论。一般而言，传统的汽车空调系统均满足上述假设，采用平面波动理论对气流脉动进行研究具有可行性。

制冷剂流动过程中，包括脉动量在内的各项物理量满足连续性方程(2)和运动方程(3)，假设制冷剂在流动过程中满足绝热可逆条件，还应满足绝热状态方程(4)。

(2)

(3)

(4)

式中u——制冷剂流速，m /s

t——时间，s

x——沿管路轴向的距离，m

ρ——制冷剂密度，kg/m3

p——制冷剂压力，Pa

k——制冷剂R134a的绝热指数，k=1.11

为了联立连续性方程与运动方程，需要利用体积弹性模量将其转化为微分方程的形式，如下

(5)

式中a——声速，即扰动传播的速度，m /s

p——制冷剂压力，Pa

ρ——制冷剂密度，kg/m3

Ev——体积弹性模量，Pa

基于假设三，制冷系统管道中的制冷剂的流动，可以看作是稳定流动和沿管道方向的小扰动的叠加，并在求解过程中，将偏微分方程中系数项中的密度视为常量。将式(5)代入式(2)和(3)中，得到

(6)

式中u*——速度脉动的时均值，m /s

t——时间，s

a——声速，即扰动传播的速度，m /s

x——沿管路轴向的距离，m

3 压力脉动模型的建立

3.1 气-液-气压力脉动模型

由于空调系统是一个封闭的循环性系统，来自压缩机排气阀的流量及压力扰动引起的声波在传播过程中，依次经过第一气相段、液相段、第二气相段后，最终又回到压缩机，被压缩气腔吸收。其中第一气相段是压缩机与冷凝器之间的高压气相管路，液相段是冷凝器与蒸发器之间的液相管路，第二气相段是蒸发器与压缩机之间的低压气相管路。从宏观上看，当汽车空调系统处于稳定工作时，制冷剂在冷凝器与蒸发器这段区间内发生相变，系统管路内液体的位置及相界面保也稳定不变，并分别与前后气相构成相界面A和B，制冷系统的扰动由压缩机产生，传播衰减之后又被压缩机吸收，重新生成一个和原来一致的扰动，如此循环往复。因此，本文提出了制冷系统气-液-气脉动模型，如图2所示。

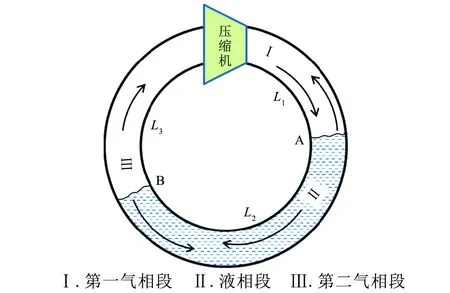
图2 空调系统气-液-气脉动模型

第一气相段存在压缩机排气阀扰动引起的正向传播的入射波以及相界面处产生的逆向传播的反射波；液相段存在来字第一气相段的正向传播的透射波和相界面处产生的逆向传播的反射波；第二气相段的气相低压管路中，扰动最终被压缩机吸收，即第二气相段只存在来自液相段的正向传播的透射波。

3.2 波动方程求解

上文提到，空调系统换热器内存在的相变界面会对气流脉动产生影响，实际上，这也正是空调系统内的气流脉动与一般空气压缩机的区别之一。汽车空调系统大多采用百叶窗平行流式换热器，制冷剂在扁管里放热相变，由于扁管较薄，尺寸大多在毫米量级，因此相界面可看作是垂直于扁管轴线。因此取第一气相段和液相分界面A为坐标轴x轴零点，考虑包含相界面前后气体和液体的微元控制体，分析第一气相段及液相段的脉动，如图3所示。

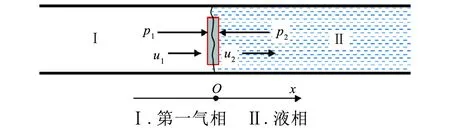
图3 气液相界面及微元控制示意图

式(6)是典型的双曲型波动方程，可用分离变量法进行求解。一般而言，波动是周期性的，因此第一气相段的脉动通解必须具有周期性。即空调系统压缩机排气管气流速度脉动可表示为

(7)

式中u1——第一气相段制冷剂速度，m/s

t——时间，s

x——沿管路轴向的距离，以第一气相段与液相段相界面处为零点，m

I1——压缩机排气口处气流速度，m/s

而当时处理这件案件的负责人正是秦明月，他严令案子没有完结之前不许其再营业。“江城故事”停业已经三个月了，店老板不知怎么就知道了秦明月是罗伽的丈夫，于是找到罗伽。尽管罗伽知道给秦明月打电话是白打，但还是忍不住打一个试试。她想，自己与秦明月冷战长达半年了，难道自己就在他面前一点影响力也没有吗？

ω——脉动角频率，rad/s

R1——由界面处反射波导致的气流速度，m/s

α1——第一气相段声速，m/s

式(7)中等号右端的两项即是式(6)的通解，第一项表示的是扰动自压缩机排气口沿管道方向传播的波，第二项表示的是入射波在冷凝器处制冷剂相变界面处产生的反射波。因此，空调系统中压缩机排气管路的气流脉动入射波与反射波共同叠加作用的结果。将式(7)带入式(2)，即可得到压缩机排气管压力脉动解

(8)

式中p1——第一气相段制冷剂压力，Pa

ρ1——第一气相段制冷剂密度，kg/m3

a1——第一气相段声速，m/s

其余参数与式(7)相同

相似地，由空调系统气-液-气脉动模型，可以给出形如式(7)和式(8)的液相段脉动方程

(9)

式中u2——液相段制冷剂速度，m/s

p2——液相段制冷剂压力，Pa

ρ2——液相段制冷剂密度，kg/m3

a2——液相段声速，m/s

T2——由第一气相段和液相段界面处折射波产生的制冷剂速度，m/s

R2——液相段和第二气相段界面处反射波导致的制冷剂速度，m/s

其余参数与式(8)相同

分析图3所示的相界面及微元体，相界面前后声压的大小必然相同，否则微元控制体的厚度趋近于零时，在控制体会产生无限大的加速度。此外，尽管制冷系统与外界的换热情况会发生改变，气液相界面的位置可能会不断地移动改变，但相界面前后气相与液相的制冷剂总会时刻保持接触，因此在相界面处气相与液相制冷剂的速度总是一致的[18]。因此，在x=0处则有以下关系式

(10)

式中u1|x=0——第一气相段与液相段界面处气相制冷剂的速度，m/s

u2|x=0——第一气相段与液相段界面处液相制冷剂的速度，m/s

p1|x=0——第一气相段与液相段界面处气相制冷剂的压力，Pa

p2|x=0——第一气相段与液相段界面处液相制冷剂的压力，Pa

任意时刻，气液界面都满足方程组(13)，因此则有以下关系式

(11)

式中I1——压缩机排气口处气流速度，m/s

R1——由界面处反射波导致的气流速度，m/s

T2——由第一气相段和液相段界面处折射波产生的制冷剂速度，m/s

R2——液相段和第二气相段界面处反射波导致的制冷剂速度，m/s

ρ1——第一气相段制冷剂密度，kg/m3

α1——第一气相段声速，m/s

ρ2——液相段制冷剂密度，kg/m3

α2——液相段声速，m/s

上式给出了相界面A前后，不同相态制冷剂的速度脉动与压力脉动的关系式，接下来分析相界面B及第二气相段的脉动关系，类比图3，以B处为坐标原点(x2=0)，则液相段与气相段的脉动方程式分别为式(12)和式(13)

(12)

(13)

式中u2——液相段制冷剂速度，m/s

t——时间，s

x2——沿管路轴向距离，以第二气相段和液相段相界面处为零点，m

ω——脉动角频率，rad/s

p2——液相段制冷剂压力，Pa

ρ2——液相段制冷剂密度，kg/m3

α2——液相段声速，m/s

T2——由第一气相段和液相段界面处折射产生的制冷剂速度，m/s

R2——液相段和第二气相段界面处反射波产生的制冷剂速度，m/s

u3——第二气相段制冷剂速度，m/s

p3——第二气相段制冷剂压力，Pa

ρ3——第二气相段制冷剂密度，kg/m3

α3——第二气相段声速，m/s

T3——液相段和第二气相段界面处折射产生的气流速度，m/s

同样，在相界面B(x2=0)处有以下类似式(10)和(11)的关系式，如下

(14)

(15)

式中u2|x2=0——第二气相段与液相段界面处液相制冷剂的速度，m/s

u3|x2=0——第二气相段与液相段界面处气相制冷剂的速度，m/s

p2|x2=0——第二气相段与液相段界面处液相制冷剂的压力，Pa

p3|x2=0——第二气相段与液相段界面处气相制冷剂的压力，Pa

其余参数与式(10)和式(11)相同

进一步由式(14)及式(15)，得到即速度反射比，

(16)

式中rv——速度反射比，即在第一气相段和液相段相界面处由反射波产生的气流速度与压缩机出口气流速度之比

tv——经相界面2次折射的速度折射比，即在第二气相段和液相段相界面处由折射产生的气流速度与压缩机出口气流速度之比

因此，式(8)可以表示为如下形式，即汽车空调系统压缩机排气管段压力脉动的近似解。

(17)

式中p1——第一气相段制冷剂压力，Pa

t——时间，s

x——沿管路轴向的距离，以第一气相段与液相段相界面处为零点，m

ρ1——第一气相段制冷剂密度，kg/m3

I1——压缩机排气口处气流速度，m/s

ω——脉动角频率，rad/s

α1——第一气相段声速，m/s

rv——速度反射比

4 结果分析

4.1 压缩机排气速度脉动求解

以上部分讨论了汽车空调内产生压力脉动的机理，这是由制冷压缩机工作特性决定的，并进一步分析了压力波在空调系统内部传播规律，表明压缩机排气口处的速度不均匀性是影响脉动量幅值大小的决定性因素。此外，式(17)表明，求解空调系统内压缩机排气管段压力脉动方程的关键，是求解未知量I1，即压缩机排气口的速度脉动。

本文研究的制冷压缩机为6气缸斜盘式压缩机，压缩机正常工作时，6个气缸依次进行吸气、压缩、排气，具有相同的工作过程，相位角依次相差60°，图1所示的气缸组件中活塞的运动规律如下

V=Rωtanβsin(ωt+φ)

(18)

式中V——活塞速度，m/s

R——斜盘半径，m

β——斜盘与转轴夹角，°

ω——斜盘旋转角速度，rad/s

φ——初始相角，rad

为了获得排气口处的速度曲线，综合活塞动力学和气缸工作过程热力学，并将气缸内气体速度近似等同于活塞速度以模拟计算排气口排气速度。图4所示为用于排气速度计算的物理模型，模型上方为6个直径32 mm，长5 mm的速度入口，模型中间为直径110 mm，长15 mm的缓冲区域，其下方为直径11 mm，长20 mm的排气口。进行网格无关性验证后，最终以201574的网格数进行求解。在FLUENT中进行求解时，采用Density Based 隐式(Implicit)求解，选择标准k-ε湍流方程模型，采用二阶迎风格式，并选取时间步长为0.0001 s对压缩工质R134a的排气过程进行瞬态求解。

在设置入口边界条件时，由于每个气缸内活塞运动规律一致，仅相角存在差异，各气缸排气时根据是否达到排气压力开启排气阀，6个速度入口只在特定时间范围内有气体进入，其他时间段的速度为0。因此本文使用UDF构造入口速度函数对6个入口速度进行定义。出口边界设为压力出口即可。

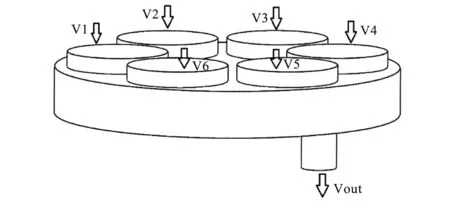
图4 6气缸斜盘式压缩机排气口模型

图5展示了1000 r/min、1500 r/min以及2000 r/min转速下，压缩机3个工作周期内的排气速度脉动情况，呈现出明显的周期性。图5表明在保持汽车空调系统的蒸发压力和冷凝压力不变的条件下，随着压缩机转速的升高，压缩机排气速度逐渐升高；同时，排气速度的脉动范围，即排气速度脉动峰峰值也逐渐增大。

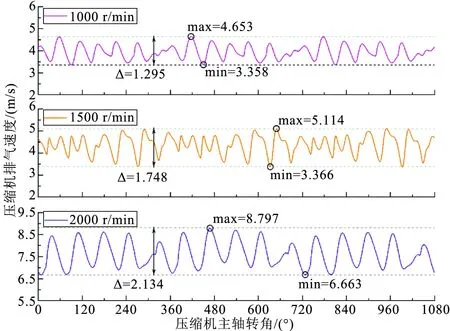
图5 不同转速下压缩机排气速度脉动

4.2 压缩机排气管两端压力脉动结果

由于汽车空调系统的压力脉动主要由压缩机排气的不连续性引起，本文着重研究压缩机排气管两端，即压缩机出口和冷凝器进口的压力脉动情况。将图5所示的压缩机排气速度脉动结果代入压缩机排气管段压力脉动方程进行求解，最终得到不同转速下压缩机3个工作周期内压缩机排气管两端的压力脉动情况如图6所示。

由图6可知，排气管内压力脉动情况与排气速度脉动情况类似，呈现出明显的周期性，且随着转速升高，压力脉动幅值增大。在每个周期内，压力脉动幅度都出现了6个峰值，这是因为本研究采用的斜盘式压缩机具有6个气缸，6个气缸以此进入排气过程，排气过程的不连续性导致排气压力脉动相应地出现6个峰值。同时在这3个转速下，压缩机排气口的气流脉动峰峰值均比冷凝器进口的气流脉动峰峰值大，脉动更剧烈，且脉动不均匀性更强，这说明压力波在空调换热器气液相界面处的反射与折射后，压力脉动趋于平缓。

同时，空调系统内压力脉动的频率也是研究关注的内容。将图6中压缩机出口处压力脉动结果进行快速傅里叶变换转换至频域，得到如图7所示的压缩机出口压力脉动幅频特性。

图7表明，压缩机排气压力脉动能量主要集中于低频段，频率在800 Hz以下。同时，在任一转速下，排气速度脉动能量都集中于1个主频率区间 (中频带) 和2个次频率区间 (低、高频带) 内，主频率区间的振幅明显高于次频率区间的振幅，包含的脉动能量更集中，如表1所示。

表1说明，低频带由压缩机运行基频产生，低频带的中心频率基本在运行基频附近。中频带的出现则是由压缩机6个气缸相继进入排气过程导致的，中频带的中心频率正是压缩机基频的6倍，而中频带也是3个频带中幅值最大的。高频带是压缩机运行基频的高阶谐量，与中频带相比较，其脉动能量发生极大的衰减，并且随着频率的增大，衰减亦更明显剧烈。Pierre Poysat和Olivier Liegeois[19]对暖通空调压缩机排气管路中气体脉动进行了实验测量和模型计算，发现实验测量的脉动时域信号与模型计算结果相比差异较大，但对频域信号进行成分分析结果证明了模型计算结果的合理性。由此，压力脉动结果在频域上与空调系统工作特点吻合，从侧面验证了气-液-气脉动模型的合理性。

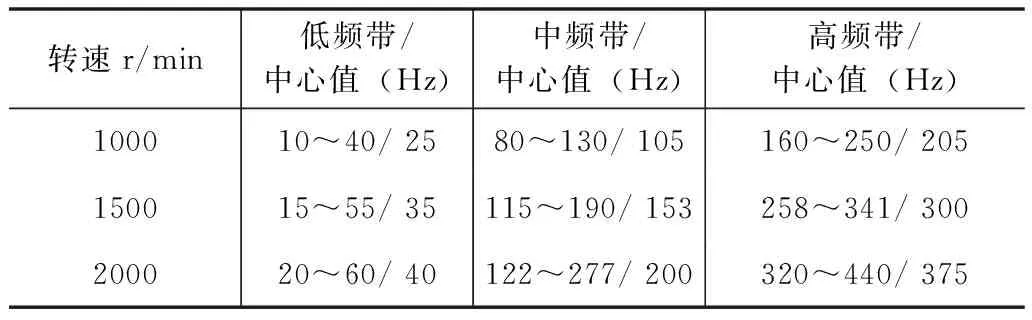
表1 压缩机出口压力脉动能量频带分布

上文提到，排管两端的压差的存在，是空调系统管路振动的主要原因。图8显示了在压缩机1个工作周期内压缩机排气管两端的压力差曲线，压差峰峰值随着转速的升高而增大，1000 r/min时排管两端压差峰峰值最小，仅为6 kPa；1500 r/min和2000 r/min的转速下，排气管两端压差峰峰值，分别为17 kPa和18 kPa。与排气管压力脉动曲线类似，在1个周期内，压差曲线同样存在6个峰值，但每个峰值之间还存在一定的波动变化，这是由压力波在相界面处的反射和折射导致的相位变化造成的。

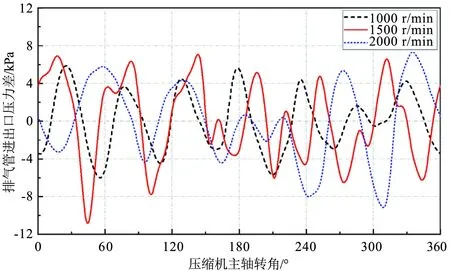
图8 汽车空调排气管两端压差

4.3 压缩机排气管路不同位置压力脉动结果

此外，本文研究了汽车空调压缩机排气管路不同位置的压力脉动峰峰值，如图9所示，排气管不同位置处的压力脉动峰峰值随压缩机排气口的距离的变化呈现出波动变化的特点；并且随着转速的提高，波动频率提高，波动更加剧烈。同时图9表明，转速越高，压缩机出口压力和冷凝器进口压力的脉动峰峰值都会增大，但冷凝器进口压力脉动峰峰值对转速的变化不敏感，始终维持在较低水平，这再次说明压力波在空调换热器气液相界面处的反射与折射后，压力脉动趋于平缓。

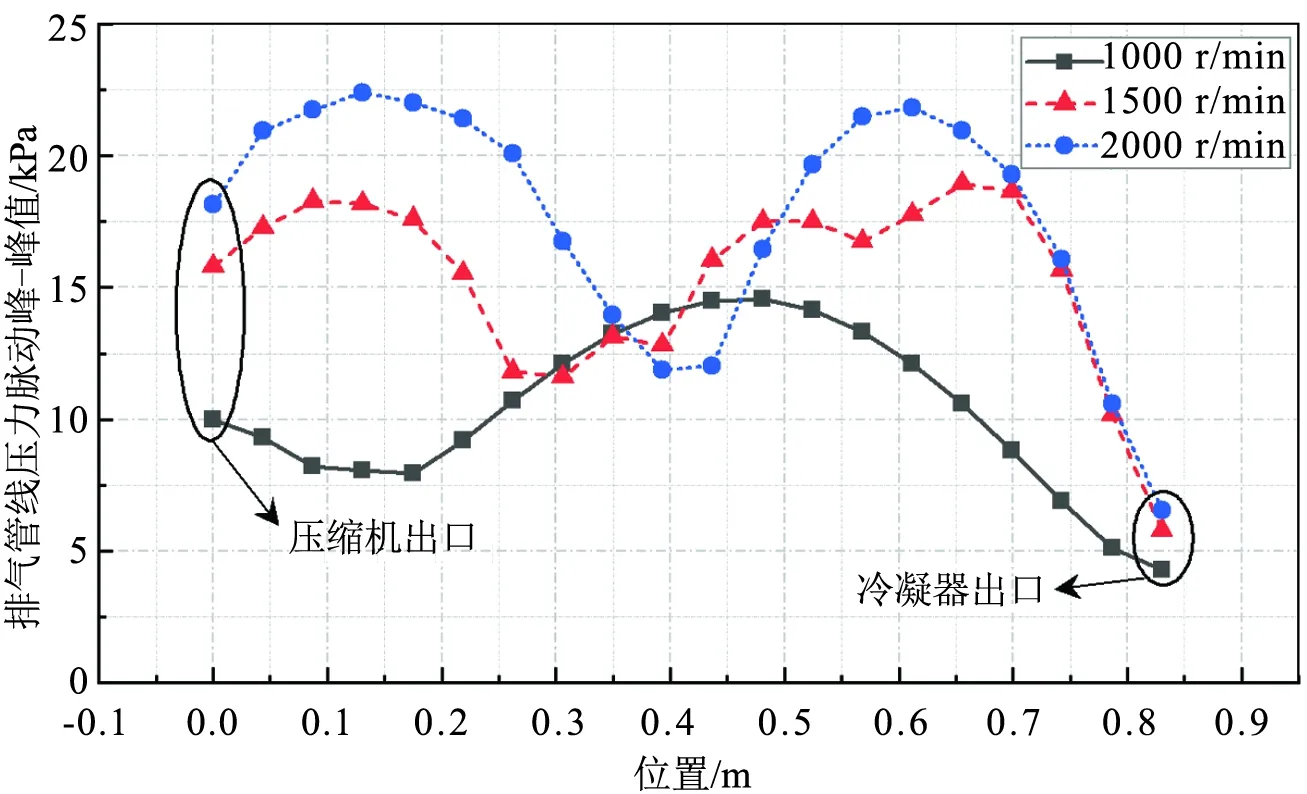
图9 压缩机排气管路各位置压力脉动峰峰值

根据气-液-气压力脉动分析模型的计算结果，得到对于汽车空调系统管路的设计具有参考作用的相关建议：

(1)选择合适的转速，尽量降低系统内压力脉动峰峰值。

(2)尽量使排气管道两端的压力脉动峰峰值及相位保持相同水平，降低两端的压差。

(3)管路存在多个弯头时，尽量保证弯头位置同时在压力脉动峰峰值曲线的波峰或波谷处，使弯头之间的压差保持在合理范围内，减小管路振动。

5 结论

本文分析了汽车空调系统压力脉动产生的原因，依据空调系统内部存在气液相界面的特点，利用平面波动理论建立了波动方程，给出了压缩机排气管压力脉动的计算方法。并对某一车型的高压排气管段的压力脉动进行了求解。结果发现：

(1)空调系统压缩机排气管段的压力具有周期性脉动的特点，这是由压缩机排气速度脉动的周期性决定的，且脉动频率在800Hz以下，属于低频脉动。

(2)压力脉动能量主要集中在低、中、高3个频率带，中频带由斜盘式压缩机的6个气缸相继进入工作过程导致，中心频率在压缩机6倍基频附近，脉动幅度最大。

(3)压缩机排气管不同位置的压力脉动存在相位差，且脉动峰峰值与其到压缩机排气口的距离有关，呈现出波动性变化；随着转速的增大，压力脉动峰峰值随位置变化的波动越剧烈，峰值越高。

(4)压缩机出口的压力脉动峰峰值始终大于冷凝器进口的压力脉动峰峰值，且随着转速增加，压缩机出口压力脉动峰峰值增加明显，冷凝器进口压力脉动峰峰值基本保持稳定。

本文提出了新的压力脉动求解模型，考虑了相界面对于压力波传播的影响，为空调系统内气流脉动的求解提供了新思路，给空调系统的管路设计提供了一定参考。