基于啮合位置相关性的双螺杆压缩机转子型线设计

王健帆，谷丽瑶，冉小平

(西南交通大学 机械工程学院，四川 成都 610036)

1 引言

双螺杆压缩机凭借着工作效率和供风质量高等优点，跻身于压缩机市场中的主导地位[1]，被广泛应用于制动、制冷等工业范畴。转子型线的设计是压缩机性能改良的关键，已经历了三次革新[2]。其中，联邦德国GHH公司开发的GHH新型不对称型线呈流线型，使螺杆压缩机的压缩效率和绝热效率有了显著提高[3]。新的不对称转子型线具有密封性好、型线类型复杂和设计难度大等特点，尽管很多学者效仿GHH型线特点设计新型线，但至今都尚未有学者对此型线的设计机理进行公开详细地解析。

为提高螺杆压缩机的性能，学者们在型线设计等方面进行了深入研究，运用最为广泛的是解析包络法[4]。在此基础上，邢子文利用常规传统的解析包络法对典型的不对称型线以及进行设计推导，演示了转子型线正向设计的一般过程，为型线的设计推导提供参考[2]。徐健将齿轮设计方法中的齿形法线法运用到螺杆转子型线的推导中去。并利用此法对复盛型线进行了详细推导，检验了齿形法线法[5]在螺杆型线推导中的方便有效性[6]。鉴于新的不对称型线组成齿曲线及方程推导的复杂性，本文在对已有典型转子型线研究的基础上，通过对阴、阳转子上组成齿曲线的旋转变换，推导变换前后的齿曲线所对应包络条件的显示变化关系，并得到变化关系式。将这个变化关系式称为啮合位置相关性，并基于此性质改进型线设计的一般过程。最后利用改进的型线设计方法对GHH型线的构型进行准确的解析与推导，并结合具体实例验证设计方法的有效快捷性。

2 啮合位置相关性

在型线推导的过程中，为了简化包络条件显示关系的推导难度，建立如图1所示齿曲线变换，设椭圆弧A2B2为阴转子上的某段组成齿曲线，其参数方程为

(1)

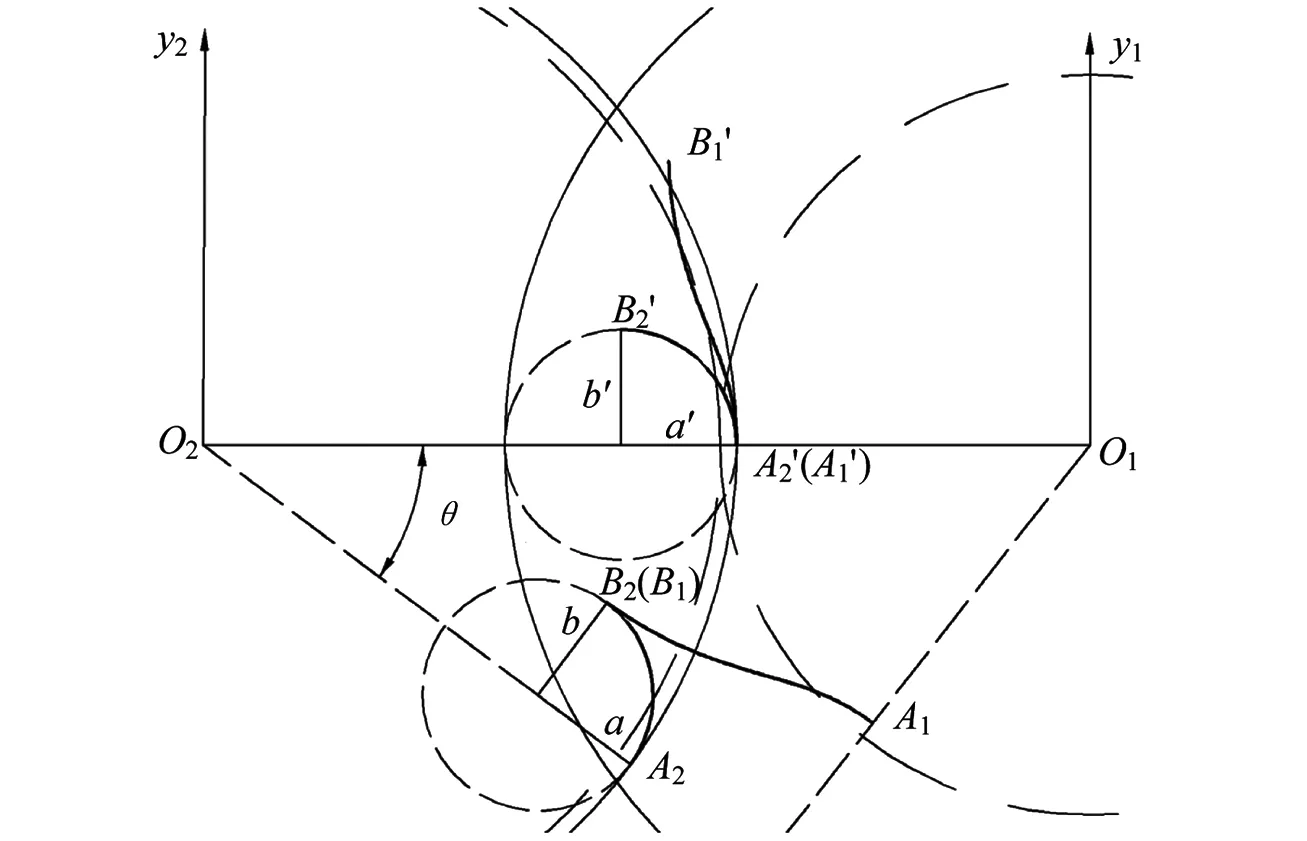
图1 椭圆弧A2B2的旋转变换

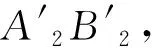
(2)

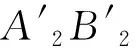
(3)

将椭圆弧A2B2带入解析包络法求解共轭曲线A1B1，其中动坐标系O2x2y2变换到动坐标系O1x1y1的变换矩阵M12及动坐标系O1x1y1变换到动坐标系O2x2y2的变换矩阵M21分别为

(4)

(5)

得到包络条件的显示关系[7]

(6)

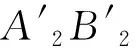
(7)

(8)

将椭圆弧A2B2带入齿形法线法求解共轭曲线A1B1，得到椭圆弧A2B2的曲线参数t与椭圆弧A2B2所在阴转子转角参数φ2的关系

(9)

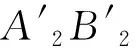
(10)

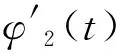
(11)

式(8)与式(11)满足φ2/φ1=i，表明2种正向设计的方法都满足啮合位置相关性的推导，也验证了啮合位置相关性的正确性。

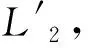
图2 改进后的型线设计流程图

3 GHH型线曲线方程

3.1 GHH型线构成

利用改进后的型线设计流程对GHH型线进行推导，典型GHH型线一对齿结构如图3所示，其型线各段组成如表1所示。

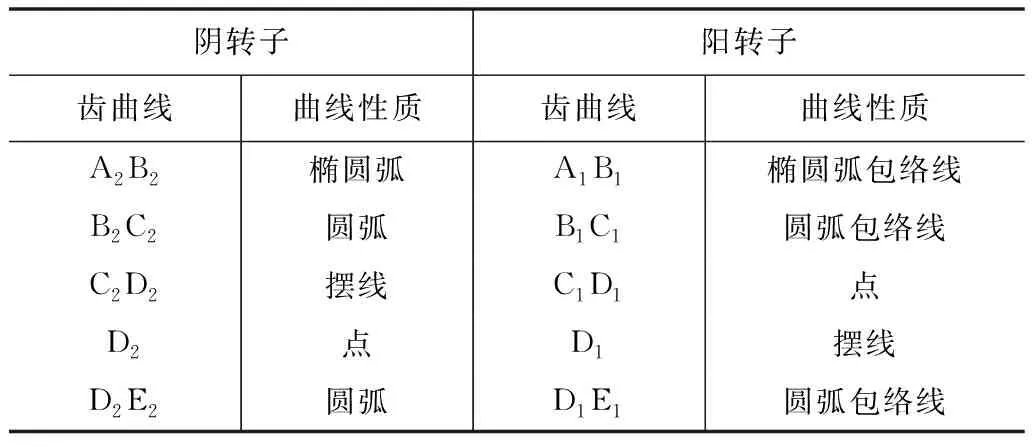
表1 GHH型线的组成曲线

根据GHH型线的构成曲线段，图3中的虚线为阴阳转子的节圆(rj)，最外围细实线为阴阳转子齿顶圆(rt)，β1、β2、α1、α2分别表示阴、阳转子齿前侧、齿后侧所夹的圆心角，并满足

(12)

图3 GHH型线构成示意图

3.2 AB和BC的曲线方程

对GHH阴转子型线结构进行分析，如图4所示。圆心M为O1O2连线与阴转子节圆线的交点，线段LMN垂直于A2O2于N，以M为圆心MC2为半径的圆(OM)交MN于B2，以N为圆心a(A2N)为长轴、b(B2N)为短轴的椭圆(ON)与圆(OM)相切与B2，且圆(OM)与阳转子齿顶圆(rt1)相切于C2点，椭圆(ON)与阴转子齿顶圆(rt2)相切与A2点。

经此几何作图后，得到A2B2型线所在椭圆方程与B2C2型线所在圆方程的相关参数为

(13)

故A2B2椭圆弧的参数方程为

(14)

以及B2C2圆弧的参数方程为

(15)

采用齿形法线法求解A1B1椭圆弧包络线时，由于A2B2曲线段为倾斜的椭圆弧，考虑对其进行旋转变换，结合图1所示，旋转矩阵的角度θ=β1。利用啮合位置相关性并联立式(2)、(7)和(8)求得

(16)

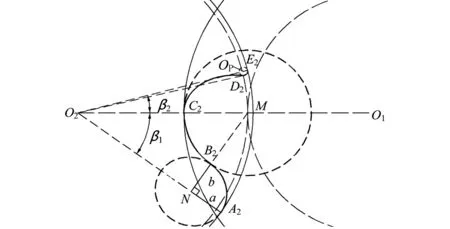
图4 GHH阴转子型线结构分析

将A2B2段型线矩阵方程左乘式(4)并联立式(16)，求得椭圆弧A2B2对应的椭圆弧包络线A1B1的方程为

(17)

圆弧B2C2为销齿圆弧型线，其共轭曲线仍为圆弧并沿着整个圆弧段同时啮合。阳转子上的曲线B1C1为阴转子上销齿圆弧B2C2的共轭曲线。故B1C1圆弧包络线的参数方程为

(18)

3.3 CD和DE的曲线方程

阳转子上的C1点是坐标系O1x1y1上的固定点，其在O1x1y1上的坐标为(-|rt1|，0)，阴转子上的摆线C2D2是阳转子上C1点相啮合的共轭曲线。由于无法满足齿形法线法求解的条件，故点摆线的求解只能运用解析包络法。将C1点矩阵方程左乘式(2)，可得C2D2摆线参数方程为

(19)

圆弧D2E2的圆心P在上齿边界线O2E2上，D2和E2分别为圆OP、摆线C2D2与阴转子的齿顶圆的G1连续点，且在连续点上一阶导数值相等，于是建立方程组

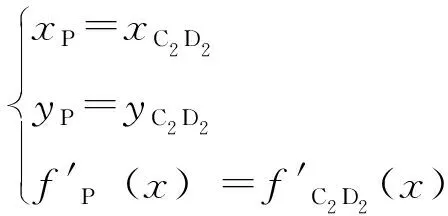
(20)

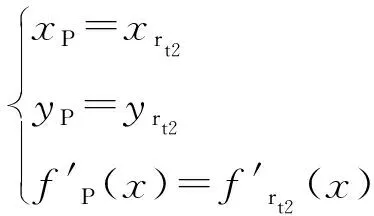
(21)

解上述非线性方程组，可直接求得摆线C2D2方程与圆弧D2E2所在圆方程的相关参数

将求得的D2(xD2,yD2)点矩阵方程左乘式(5)可求得其对应的共轭曲线C1D1的参数方程为

(23)

由式(22)可得D2E2圆弧的参数方程为

(24)

将圆弧D2E2进行旋转变换，旋转矩阵的角度θ=-β2。参考A1B1段椭圆弧包络线求法，求得D1E1圆弧包络线的方程为

(25)

3.4 GHH型线具体算例

取阳转子齿数Z1=5，阴转子齿数Z2=7，中心距A=206 mm，阳、阴转子齿顶圆半径rt1=131 mm、rt2=124 mm，可计算出以下参数见表2：

其中阴转子型线设计的唯一逻辑为：先确定摆线C2D2以获得D2点，再确定圆弧D2E2方程以获得齿后角β2，进而得到齿前角β1，以及椭圆弧A2B2、圆弧B2C2的几何参数，最终得到整个阴转子型线的构型。利用UG软件曲线分析中的连续性和曲率梳对本文设计的阴转子型线进行连续性分析如图5所示，可得到阴转子型线的连续性为G1连续，满足螺杆转子型线设计的要求，表明阴转子设计的正确性。

表2 GHH型线算例相关参数

结合阴、阳转子型线的构成及型线结构分析的结果，建立阴、阳转子啮合时的三维模型如图6(a)所示，并获得其空间啮合线如图6(b)所示。阳转子对阴转子的包络过程如图7所示，显示啮合过程无干涉现象，表明阳转子型线推导的正确性[8]。

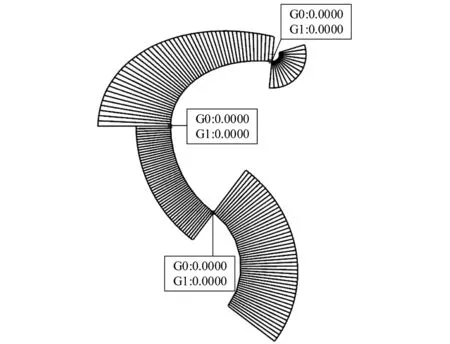
图5 阴转子型线的连续性

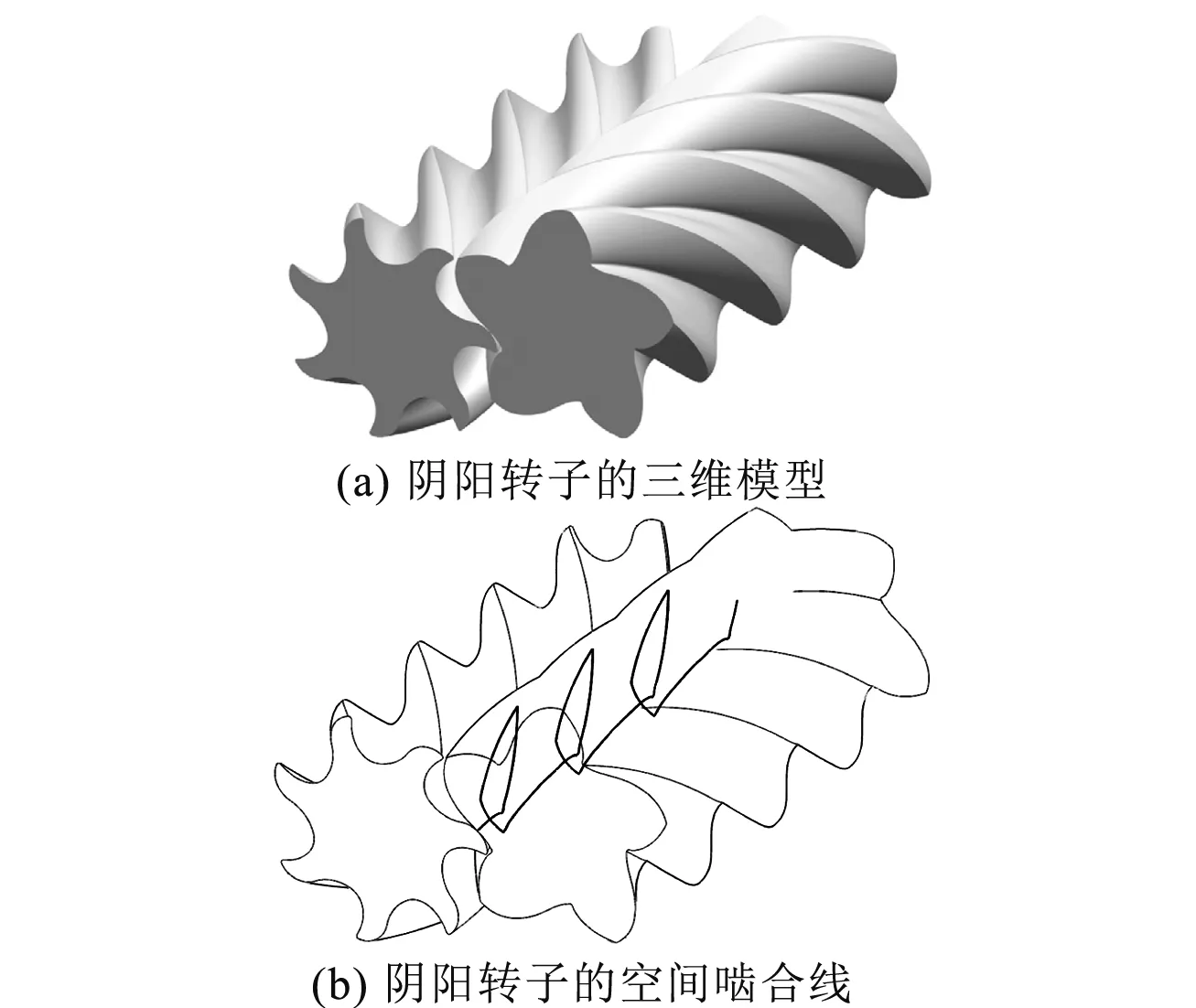
图6 阴阳转子的三维特征

4 结论

(1)利用齿曲线的旋转变换，得到变换前后曲线参数和与其对应的转子转角参数的变化关系，即啮合位置相关性，并利用解析包络法和齿形法线法验证了啮合位置相关性的正确性。

(2)利用啮合位置相关性对双螺杆压缩机转子型线设计过程进行改进，减小了新型不对称型线中复杂组成齿曲线推导的困难，缩短了型线设计的时间成本。

(3)利用改进的型线设计过程以及方法推导出了GHH型线，精确揭示了GHH型线的构造特点，为现代转子型线的设计提供参考。