MD2.5隔膜压缩机膜片的有限元分析

郝 莉，巴 鹏

(沈阳理工大学机械工程学院，辽宁 沈阳 110000)

1 引言

隔膜压缩机是重要氢能输送设备。该种压缩方法无二次污染，对于压缩气体有十分好的保护作用，它的特点是密封性好、压缩比大、润滑油以及固体杂质不能污染压缩气体。适合应用压缩具有很高的纯度、十分稀有的和贵重的、容易燃烧爆炸的、有毒有害的、有腐蚀性的，压力很高的气体。

隔膜压缩机是一种结构特殊的容积式压缩机[1]，油通过配油板推动膜腔内膜片的往复运动，改变气缸和气腔的容积，在吸气阀和排气阀共同工作下，实现气体的压缩和输送。故膜片是隔膜压缩机运行过程中最关键也是最容易发生破坏的元件，膜片的情况关系到隔膜压缩机的正常运行与否，严重的会带来巨大的经济损失。对于广泛使用的金属膜片，扭转弯曲、坍塌、裂纹和机械疲劳是膜片损坏的主要表现[2]。

国内和国外的学者们通过各种研究分析膜片的性能。王迪生等[3]利用多种功能，在间隔内通过平滑连接改变膜腔表面。新表面上膜的应力相对均匀，外缘的应力幅度较小，气腔的表面积也增大。Mathew，B.等[4]特别指出，在实现隔膜压缩机小型化设计的过程中，材料的选择、几何参数的设计和运行条件对机器的工作性能有一定的影响。安代明等[5]试图提高轴类零件的耐磨性，这对活塞杆激光淬火工艺机理和表面预处理方法非常有利。李霁阳等[6]在优化膜腔轮廓时，基于膜的偏转理论。

综合上述研究，由于受力，隔膜压缩机的周边固定的膜片会产生形变，严重的会发生破裂，相同材料，相同尺寸，膜片上下表面的压力差越大，膜片的变形越严重，相同尺寸，相同材料，相同压差下的膜片变形越大，由于膜片的变形不是线性的，故受力分析是十分复杂的，因此，我们要对膜片的受力的情况进行分析，从中找到膜片在什么位置出现最大的变形。

2 膜片的受力分析

隔膜压缩机的膜片基本都是是由金属材料制作的，膜片周围由盖板及底座固定，在工作过程中由于受到气腔和油腔的压力差形成的力而鼓起变形，如图1所示，一般情况下对于同类型的膜片，所受的力越大，则该膜片的形变量越大。膜片的薄厚对形变也有很大的影响，由于为非线性关系，所以膜片受力形变的情况较为复杂，下面就是借助板壳力学对膜片受力的情况进行理论研究[7]。

图1 隔膜压缩机膜片在压力差作用下的鼓起变形

2.1 膜片的剪力和弯矩分析

剪力和弯矩都作用在膜片上。绘制时，横坐标为垂直于横隔板轴线方向上的剪力或弯矩，制出剪力图FQ(x)和弯矩图M。

膜片受到均布载荷时的剪力图和弯矩图如图2所示。

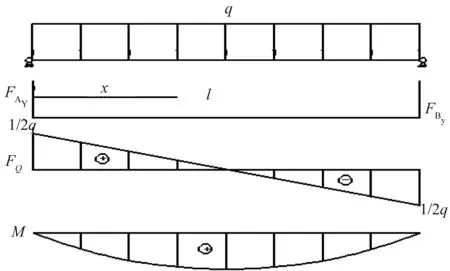
图2 均布载荷作用的剪力图和弯矩图

(1)求约束反力，得

(1)

(2)列剪力方程和弯矩方程

(2)

(3)

(4)

2.2 薄膜挠度方程与作用力的关系

对于隔膜压缩机，当膜片厚度为0.3～0.5 mm时，中心挠度可达5～10 mm，因此，研究膜片形变不能运用小挠度的理论[7]。故可以求得薄膜从水平位置向上运动过程中的各位置的挠度方程，即

W=Wmax(1-X2)2

(5)

膜片挠度与压力的关系式

(6)

2.3 膜片的应力分析

一个微小单元体在膜片上切出，周向的正应力、径向的正应力和剪应力都是这个微小单元体所承受的，不存在周向剪切应力，如图3膜片应力分析图。径向法向应力和周向法向应力也可视为弯曲和拉伸引起的法向应力之和[8]。由虎克定律，弯曲应力被分解为

(7)

(8)

由板壳力学求出膜片拉伸应力的微分方程

(9)

式中φ=G(r)，是应力函数。

图3 膜片应力分析图

故可以解得

径向总应力

(10)

其中

(11)

同理，周向总应力

(12)

其中

(13)

故可以根据膜片任意处的应力求出该点处薄膜的应变值。

3 MD2.5隔膜压缩机的三层膜片力学分析

对MD2.5隔膜压缩机的隔膜状态进行了应力分析。具体参数如表1所示。

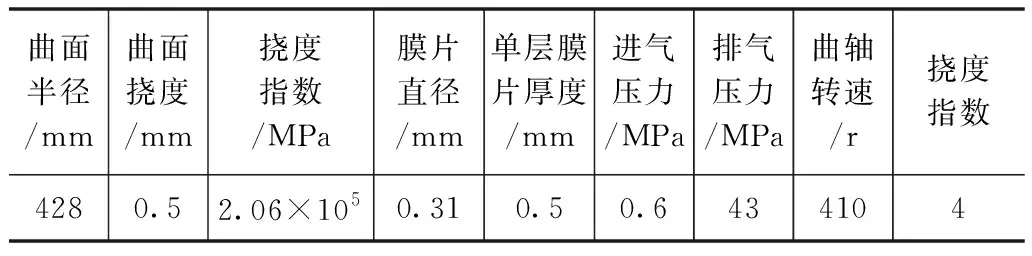
表1 MD2.5隔膜压缩机的各项参数

3.1 膜片运动行程中的挠度曲线

薄膜片向上运动行程中的挠度变化曲线方程

W=Wmax(1-X2)2

(14)

(15)

任意选取膜片运动行程中挠度为1 mm、2 mm、3 mm的膜片挠度方程进行分析，即

(16)

(17)

(18)

根据压缩机设计手册中的挠度方程设计得到气腔曲线

(19)

将最大挠度Wmax=5.9 mm和挠度指数z=4代入上式，挠度方程曲线与气腔曲面一致，即

(20)

3.2 不同挠度下的膜片应力应变分布情况

三层隔膜中每个隔膜的应力和挠度曲线相同，因此只需计算任何隔膜的应力应变值即可。将板壳力学中最大挠度为5.9 mm时的挠度曲线代入拉应力微分方程[9]。

当隔膜组向上移动时，隔膜上表面的应力最大，而隔膜下表面的应力最小，即

径向应力

(21)

(22)

周向应力

(23)

(24)

将弹性模量E=193000 MPa，曲面半径R=204 mm代入(21)和(22)，画出膜片上表面和下表面的径向应力的分布图，如图4。

由图4可得，最小径向应力和最大径向应力分别在膜片的边缘和中心出现。

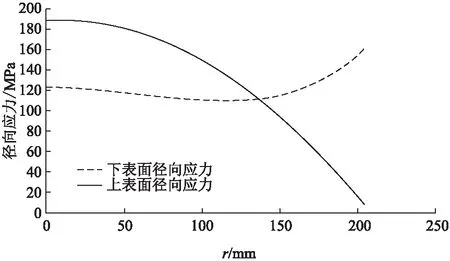
图4 挠度为5.9 mm时径向应力分布

交点处为膜片形变的拐点，这一点处的径向应力的值相等，弯曲应力为0，即

(25)

按上述情况绘制出膜片上下表面的周向应力分布图，如图5。

由图5可知，隔膜中心的周向应力最大，隔膜边缘附近的值最小。径向和周向应变值根据膜片上的径向和周向应力值以及广义胡克定律计算，即

(26)

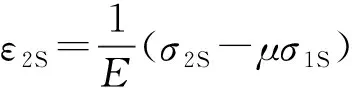
(27)

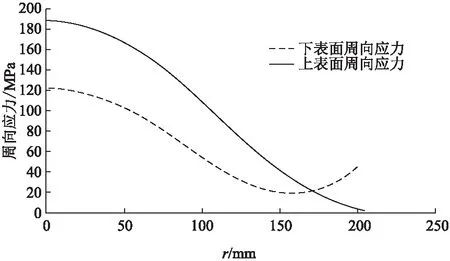
图5 挠度为5.9 mm时周向应力分布

如图6，根据上述公式可得上下表面应变分布曲线，挠度为5.9 mm。

如图，膜片应变与应力值变化类似。

图6 挠度为5.9 mm时上下表面应变分布

4 膜片的有限元分析

4.1 有限元分析模型的建立

有限元分析模型采用的研究对象是MD2.5隔膜压缩机的膜片，参数如上表1。

为了对膜片使用ANSYS软件进行静力学有限元分析，对膜片的形变和受力作出如下假设：

(1)将圆形膜片上的其它材料忽略；

(2)忽略圆形膜片上的牵引力[10]。

分别在膜片的中心和膜片的边缘施加力，并对其进行静力学的分析。

4.2 结果分析

4.2.1 膜片的等效应力分析

膜片在交变载荷的作用下偏转。根据拉弯作用，膜片在边缘处承受最大的应力。根据图8和图9，隔膜中部变形，周边固定，隔膜边缘附近形成拐点，更容易破裂[11]。从图中可以看出，最大的挠度时2种不同力作用的膜片，应力分布是不均匀的，这2种情况时最大应力都位于膜片边缘处，即膜片最可能在此处发生最大破坏。

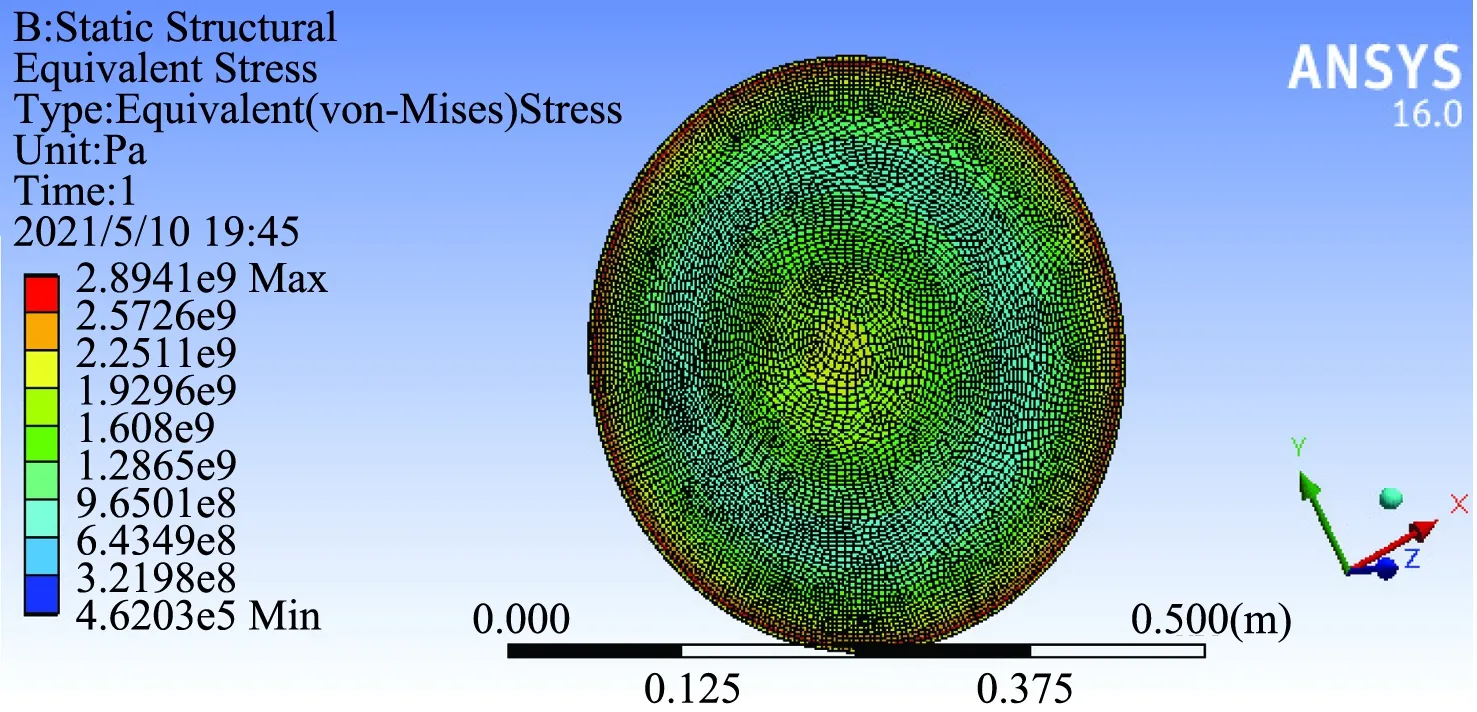
图8 在膜片中心上施加力的等效应力图

图9 在膜片边缘上施加力的等效应力图

4.2.2 膜片等效弹性变形分析

通过有限元计算得到膜片的等效弹性变形状态，如图10、11所示。应力集中现象出现在膜片边缘，膜片最大应力的位置与其相同，膜片在这个位置破坏最有可能。本文分别在膜片的中心和边缘施加力，但是其他条件时不变的。

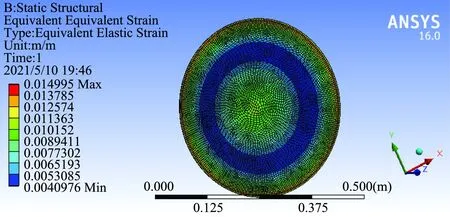
图10 在膜片中间施加力的等效弹性变形

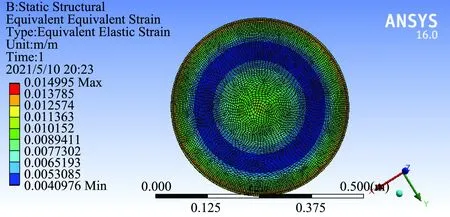
图11 在膜片边缘施加力的等效弹性变形

5 结论

(1)在实际工作中，应力集中出现在膜片上的边缘处，工作一定时间后，不断积累损伤会导致膜片的疲劳破坏。

(2)对膜片进行理论分析，然后通过ANSYS对膜片进行有限元计算，得出膜片应力最集中的位置。

(3)在零件的实际设计和生产中，当根据载荷满足材料的静强度要求时，应优先考虑其疲劳寿命。