演绎数学思维 提升数学能力
——以一道平面向量的数量积问题为例
福建 卢秀敏 包 喜
数学二轮复习主要是以专题为主、微专题为辅,以突破核心考点、提升关键能力为宗旨,以丰富的数学文化为底蕴,以不同视角的解题思想和方法为平台,演绎数学思维的多彩多姿.本文选取一道平面向量的数量积求最值问题,深挖例题的示范作用和延伸价值,整合二轮复习时的例题知识容量,综合提升数学关键能力.
向量是数学领域中一个重要工具,它既从“大小”这个代数角度,又从“方向”这个几何角度,赋予研究对象丰富的研究视角,让数学研究对象鲜活灵动起来.对平面向量的考查中,又是以其数量积的运算为主.向量的数量积有代数运算:a·b=|a|·|b|·cos
一、问题呈现

( )



此题响应新高考命题要求,源于生活,用于生活.以体育运动中的自行车为模型,以等边三角形与圆这两个平面几何图形为问题背景,通过圆上动点与圆外定点的位置关系进行合理渗透,通过圆上动点绕圆心运动的变化过程,以平面向量数量积的运算为平台,考查其变化结果的最大值问题.
破解该题时,可以依据平面向量数量积的“代数”关系进行切入,借助函数思维,利用三角函数、柯西不等式,通过数量积的坐标运算,结合三角函数的值域、不等关系来分析与求解;可以利用平面几何图形的“几何”特征,借助数量积的几何意义、线性规划的技巧,运用极限思想寻找最值情况.
二、问题破解
1.思维视角一:紧抓“代数”关系——函数思维
解法1:坐标法

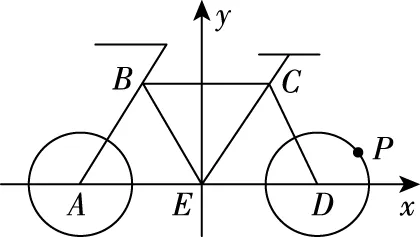
点评:本解法通过建系设点,将所要研究的向量数量积、动点所在的圆坐标化,依据双变量求最值的问题导向,采用三角换元,换双变量x0,y0为单变量θ,再根据辅助角公式转化目标函数,由余弦函数的最值得目标函数的最值.此解法思路简单、方法老套,但“少思则多算”,解题过程冗长烦琐,需要具备较好的运算求解能力.
解法2:向量法

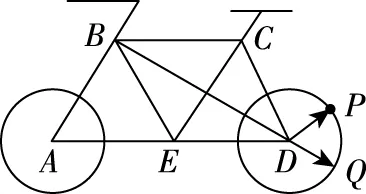
点评:本解法通过分析三角形之间的边角关系,将未知模长与方向的向量化为已知模长与夹角的向量,转换研究对象,化繁为简,化动为静,以三角函数呈现研究结果,结合余弦函数的最值求得目标函数的最值.此解法灵巧方便,但“少算”则需“多思”,解题之前需细细思量研究对象在平面图形中的位置关系,以静制动,需要良好的推理论证、抽象概括能力.
解法3:不等式法



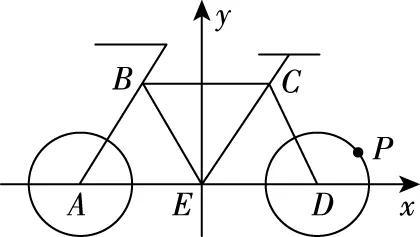
点评:本解法在建系设点之后,将研究对象平面向量的数量积通过坐标实现了代数化,联系目标函数与动点轨迹方程之间的代数关联性,构造柯西不等式的结构模型,借助柯西不等式求得目标函数的最值.此解法巧妙建立数学模型,巧借数学公式,轻松化解目标求解过程,对数学建模核心素养提出了较高的要求.
2.思维视角二:细看“几何”特征——几何思维
解法4:线性规划法


点评:本解法在建系设点之后,按部就班地将平面向量的数量积转化为坐标运算,再依据线性规划的原理,将线性目标的最值转化为直线与圆的位置关系,最后通过圆心到直线的距离等于半径的关系,解得目标函数的最大值.此解法重在分析研究目标的“线性”几何特征,动点的“圆形”几何特征,故对数学抽象、直观想象的数学核心素养提出了较高的要求.
解法5:几何投影法
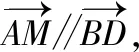

点评:本解法从向量的数量积的几何意义,通过投影的变化过程,直观感知投影变化的最值情况,代入公式可得结论.此解法形象易懂,依据简单,主要考查对数学运算对象的法则理解,对数学研究对象的基本了解,体现了数学概念的重要性,对空间想象与抽象概括能力有基本性的要求.
三、变式拓展

变式2:将题设条件中的圆D轨迹改为抛物线y2=2px(p>0),则目标函数应相应改为以y0为自变量的二次函数,利用二次函数的模型求得最值.

变式目的:将解析几何的基本图形嫁接到本题的题干中,促进学生学习能力上的知识迁移能力,在不变的思维方式上,体验不断变化的问题环境,体会数学思维与能力的无限空间.
四、教学启示
1.向学科知识要精度
数学是高度抽象、强调逻辑,有一套自己的语言系统的学科.每一个数学概念都是数学家们经过无数次的验证、完善形成的,其精确度是经历几百年的历史论证的.在数学解题之前,必须明确每一个数学概念的内涵与外延,二轮复习的教学中也要优先引导学生进行“四个追问”:追问核心考点的准确表述;追问核心考点的理解程度;追问核心考点的应用价值;追问核心考点的使用方法.李士锜教授在其《熟能生巧吗?》的文章中,提出“数学只有被深刻理解了,才具有迁移与应用的活性.”对数学概念的精细化理解有助于解题方向的明确,有助于解题方法的简化.
2.向学科能力要广度
数学的研究方法是丰富多彩的,“多思少算”“少思多算”是区分学科能力形成的一个标准.数学学科中抽象概括能力考查学生的数学阅读能力,将文字与符号转化为数学思维;空间想象能力考查几何问题的知识迁移到代数运算;运算求解能力引导数据处理能力与推理论证能力的综合应用,实现用数据说话的数学学科作用;应用与创新能力促进数学学科在不同领域的扩展与延伸.不同角度地观察同一个研究对象,可有不同的视角下的不同理解,有助于不同学科能力的同步提升.
3.向优等生培养要深度
习主席说:“当今世界的竞争说到底就是人才竞争、教育竞争.”数学作为基础学科,在国家强基计划中占据首位,它对人才的培养起着至关重要的作用.对于二轮复习的课堂例题,在讲解分析的过程中,随时对条件的观察,联想与之有关的结论,这应该是优秀学生必须具备的一种思维习惯.苏霍姆林斯基说思维培养的最好方式是“一边思考、一边观察,在观察中思考,在思考中观察.”二轮教学要根据学情,以培养数学优等生为目标,不断拓展思维深度,塑造优秀的数学人才.
4.向学科素养要高度
学科核心素养是学生在接受学科教育的过程中,逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力.站在学科素养的高度,审视高三二轮复习的例题讲解,可有效综合不同知识点之间的融合,如本题的平面向量、三角函数、不等式、线性规划、解析几何,奇妙地展示了数学思维的灵活转换,吸引了学生对数学探究的兴趣,提升其数学研究的能力,培养多方面的学科核心素养.
五、结束语


