引学生追溯知识之源 助学生化解学习之困

周新改

在小学数学教学中有许多公认的学习难点，可以称作是“经典”难点。从大量的公开课或常规课来看，执教者要么淡化处理，要么“告知”学生。这样做不仅窄化了教学空间、堵塞了学生思考的通道，而且会挫伤学生学习数学的积极性，不利于学生思维的发展，让学生潜意识地认为数学是无根无源的、数学学习是不讲道理的、数学学习是死记硬背的。本文就结合笔者个人的教学实践浅谈自己引导学生追溯知识的本源，帮助学生化解学习难点的一些做法及体会。

一、对接生活，追根溯源

我们知道，二年级学生在《初步认识角》一课的学习中很难理解“角的大小与边的长短无关”的道理。不少老师借助这样的演示帮助学生理解：把老师的三角尺教具和学生的三角尺学具中的大小相同的角重合，力图让学生看到“老师三角尺中的一个角和学生三角尺中的一个角完全重合，而老师三角尺中的这个角两边比学生三角尺中的那个角两边要长，不就说明角的大小与边的长短无关吗？从课堂反馈来看，学生仍是满脸茫然。殊不知，这样的演示让学生看到的是“面”的比较，更没有看到“完全重合”，反而造成了学生对“角”与“面”的认知混淆。

也有很多老师只引导学生利用“活动角”直观感受角的大小是与边的张合有关，却不引导学生体会角的大小与边的长短无关。

学生面对画在纸面上的“静态角”，难以摆脱其边的长短以及表面上的大小所带来的非本质属性的干扰，排除这个负面干扰，仍要回到“角”是怎样抽象出来的源头去。

请看我教学这部分的片段。

师（指三角板中的一个角）：谁能把这个角画在黑板上？

学生到黑板上利用三角板画出老师指的角。

师：我也把这个角画出来。

师仿照学生的画法也画出了这个角（但和学生所画的角的边长度不同）。

问学生：这两个角，哪个大，哪个小？

因为老师和学生画的是三角板的同一个角，有了“画同一个角”做载体，课堂上这样的声音多了：画的是同一个角，所以这两个角同样大。不仅有结论，而且有道理。

我不急于说出学生心目中想要的答案。

转身在黑板上先写了一个小一些的“3”，在它的旁边又写了一个大大的“3”。

问学生：这两个写得大小不同的“3”，哪个“3”大一些？

生齐答：一样大。

追问：咦？明明一个“3”写得那么大，另一个“3”写得这么小，怎么能相等呢？

生：虽然写得大小不同，但都表示3个一，所以相等。

顺着学生的回答，我在两个“3”之间写上“=”。

至此，学生感受到“大”和“小”又有了不寻常的意义。

师：数的大小是指这个数所包含的个数的大小，与写得大小无关，那角的大小又是指角哪里的大小？与角的哪儿无关？

学生纷纷发表自己的见解，还迫不及待地边打手势边说：角的大小是指角的两边张开的大小，与边的长短无关。

看来，学生对于“大”和“小”的认识正在变得全面而深刻。

杜威说：“教育就是经验的改造和重组。”儿童的生活经验和认知缺陷经常会干扰对数学知识本质属性的理解。立足儿童的心理特点，基于数学的学科特征，设计相应的活动，不仅对知识进行抽象，还要对知识进行还原，让学生回到知识产生的源头，经历知识产生的过程，由直观感知逐步走向数学抽象，不断修正错误的认知，感悟数学概念的本质。

二、联系对比，追根溯源

苏教版五年级下册第30页《因数与倍数》这一单元开始有一处注释：

*研究因数与倍数时，所说的数一般指不是0的自然数。

教师们都知道这是一个数学“规定”，却不研究规定背后的道理，教学中只是补充告诉学生，而且“以书为证”。那么学生对于这样“规定”的科学性与合理性就无从认识和理解，让学生潜意识里以为数学是不讲理的，这不是数学应有的面貌。

下面，我提供一个版本，大家可以讨论，是否可以帮助学生理解这个规定？

学生在学习了“因数和倍数”的概念后。

师：同学们，你们自己能独立写出一道算式并说出算式中的数具有怎样的因数与倍数关系吗？

生交流，说的也都是各部分是整数的乘法或除法算式。学生对于概念意义的表面模仿还是很强的。

师：看来，因数和倍数这两个概念是建立在我们学习过的什么运算的基础上？

生：乘法或除法。

师：你能用一句话概括乘法算式中三个数之间具有怎样的因数和倍数关系吗？

生：在乘法算式中，两个乘数都是积的因数，积是这两个乘数的倍数。

师：除法算式中呢？

生：在除法算式中，除数和商都是被除数的因数，被除数是商和除数的倍数。

师：我写两个算式，请你们来说说这两个算式中的各个数具有怎样的因数和倍数关系。

板书：2×5=10，10×0.2=2

对于第一个算式，学生都特别容易回答了;对于第二个算式，有受思维定势干扰的学生立刻按照形式说：10和0.2是2的因数，2是10和0.2的倍数。（说完，自己也吐了吐舌头）

马上有学生反对：怎么一会儿10是2的倍数，一会儿2是10的倍数？

师故作惊讶：是呀！怎么会有这样的数学呢？不是矛盾嗎？

学生们议论开来，有的说不可能，有的自言自语：怎么回事呢？也有看过书中注释的同学恍然大悟：怪不得呢！

我请同学们发表自己的想法、看法。

生1：这样不是乱套了吗？

生2（举着课本兴奋地）：书中已经规定了“研究因数和倍数时，所说的数一般是指不是0的自然数。”

生3：就好像“0不能作为除数”一样，是为了不产生矛盾。

生4：我来补充，只能说2是10的0.2倍，但不能说2是10的倍数，因为它还没到10的1倍。

师：是呀！为了不产生矛盾，便于研究，所以才有了“研究因数和倍数时，所说的数一般指不是0的自然数”的规定。

学生找到了这个“规定”的“源头”，对概念的理解就会更加深刻。

其实，任何数学规定产生的背后都有一定的原因和道理、一定的合理性与必要性，作为教师，应努力引导学生去探索、理解、体会“规定”产生的过程，让学生感受到数学知识内在的严谨性，感受到相关“规定”背后的数学道理，从而形成更加合理的认知结构，获得更多有价值的感悟。

三、经验倒转，追根溯源

有经验的教师都知道，教学《分数的意义》最难突破的是学生对单位“1”意义的构建。许多教师是在学生认识分数的基础上，总结性地、讲述式地告诉学生：像图中的一个物体、一个图形、一个计量单位或由许多物体组成的一个整体，都可以用自然数1来表示，通常叫作单位“1”。继而再让学生举例说说单位“1”还可以是什么。学生抽象单位“1”的思维过程被教师的一句话代替了，学生处于被动接受知识的位置，单位“1”好像是从天而降的“怪物”！试想：这样缺乏学生主动思考的学习，还怎么会有经历？怎么会有体验？怎么形成经验？

接下来就说说我是怎样引导学生抽象出单位“1”的。

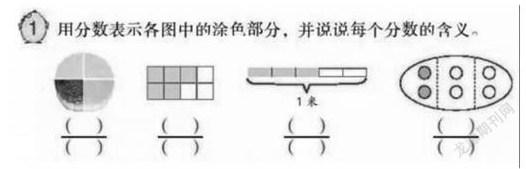
如下图，要求学生自主完成例1中的填空，集体交流说出每个分数的意义。

我利用学生已有的分数认知经验，引导学生再回来逐一深入研究每一幅图。

师：把一块饼平均分成4份，其中一份用表示，其中的2份、3份、4份各怎样表示？为什么？

生1：1份是，2份是，3份是，4份是，有几份就是几个。

生2：我觉得4份是，也就是1。

师：大家觉得呢？

学生进行充分地交流讨论得出：4份合起来不就是原来的一块饼吗？就可以用“1”来表示。

第一幅图突破了，第二、三幅图同理。并明确：1块饼、1个长方形、1个长度单位都可以用“1”来表示。

最后一幅图稍遇障碍。

师：这6个圆片该用哪个数来表示呢？

生1：用6来表示。

生2：（疑惑地）我感觉还应该用1来表示吧？

真好！出现了不同的观点。

师：还是大家一起讨论，但要说出用这个数来表示的道理。

不一会儿，意见就统一了，原来认为用6来表示的同学说：我忘记了这里的2个圆片是用来表示的了，3个合起来是   ，也就是1。

师：看来1的意义真广呀！不仅可以表示1个物体、1个长方形、1个长度单位，还可以表示——

生（齐答）：6个物体组成的一个整体。

师：联想一年级时学习的1，这几幅图里的“1”又有什么不同？

生：一年级学习的1就代表一个物体，而这里的1还可以表示很多物体。

师：用1来表示很多物体时，是把很多个物体组成一个——

生（齐答）：一个整体。

师：你还能举例说说用1来表示许多物体组成的一个整体的事情吗？

学生纷纷举例，有一堆苹果、一堆沙、一条路、一个班的学生、一个学校的学生、一个城市的人口——都可以看作1。

单位“1”的意义呼之欲出。

师：此时的“1”非彼时的“1”，意义更广泛，数学上叫单位“1”。

单位“1”的意义已经在学生的思维里生长出来，分数意义的形成还有困难吗？唤醒学生已有的认知分数经验，引导学生的思维倒转到知识发生的“源头”，深深体会到平均分是单位“1”，平均分后得到的分数都是单位“1”的一部分。“1”不断累加得到整数，“1”平均分后得到分數，“1”是整数的根基，也是分数产生的根基。有了这样的理解和认识，就能很好地为学生后续的学习赋能。

学生学习任何知识都应该是自然的、自觉的，面对学生学习中的难点，要联系所学知识的“前世今生”，结合学生的认知规律，思考我们的教学路径，把数学学习从哪里来、到哪里去，梳理清晰明白。从学生的已知出发，引导学生到未知的领域探索。