设计多样化活动，促进学生深入认识轴对称图形

张静

[摘  要] 设计多样化的数学活动是使小学数学教学的有效性得以提高的基本手段。因此，在教学中教师需要重视观察、实践、创作等一系列的学习探究活动，让小学生在活动中获得不同的体验和更为丰富的学习感知，为他们感悟新知、提炼和归纳数学概念提供最为强劲的助力，从而让学生的数学学习不断深入，也使得他们的数学思维和数学素养得以不断发展。

[关键词] 数学活动;轴对称图形;认识

在苏教版六年级数学教材中有一个“图形的运动”章节，其设计目的是让学生通过对图形的运动识别和理解来较好地认识丰富多彩的现实世界，体味自然之美、图形之美和运动之美，并以此为契机，引导学生更好地探究图形运动的过程，感悟图形运动的空间属性，从而帮助他们形成初步的空间观念，有序发展他们的空间意识。在此，笔者结合“轴对称图形的认识”的教学，简略地梳理几何图形运动对学生感悟对称美的促进作用，以及这样的几何图形运动对学生空间观念的初步形成所产生的积极且深远的意义。

[⇩] 一、在观察中感知轴对称

平移和旋转是平面图形最为常见的运动，其间图形的形状、大小没有丝毫的变化，发生变化的仅是图形的位置。通过观察图形的运动过程，无疑能够较好地帮助学生体会空间的存在，感受图形与空间的关系。轴对称看似与平移和旋转不尽相同，但是只要我们深度研读概念，不难发现轴对称的本质也是一种图形的变化运动，它是以某一条直线为对称轴，并围绕此轴将图形在三维空间进行翻转，由此实现对应点连线与对称轴垂直、对应点到对称轴之间的距离相等。从中我们不难发现，轴对称这一运动远比平移和旋转来得更抽象一些，所以在教学中教师要重视对学生观察比较的指导与引领，以帮助学生更好地感知轴对称图形，初步形成空间观念。

师：观察屏幕上的图形（如图1），说说自己的感受。

生1：第一个图形是一只漂亮的蝴蝶。

生2：中间那个好像是北京的天坛。

生3：最后一个我知道，那是一架超级棒的战斗机。

师：那这三个图形之间有没有什么共同之处呢？小组交流一下，看看会有什么发现。

生4：蝴蝶两边的图案是一样的，所以很漂亮。

生5：天坛也是可以分成左右两部分，左右两边也是一模一样的。

生6：飞机也是可以分成上下两部分，这两部分也是一模一样的。

……

师：观察得真仔细！那么联系一下自己的生活，在你的身边你见过类似的东西吗？

生7：我穿的这件衣服就是和蝴蝶形状差不多的，它左右两边的样式和图案都是一样的。

生8：这样的东西很多，比如五角星也是可以分成两部分的，而且这两部分是一模一样的;英文字母M、O、T等也是可以分成两部分的，而且这两部分也是一模一样的。

生9：是的，像银杏叶子、枫叶等也具有这样特点。

……

轴对称图形的知识看似简单易懂，但是学生要真正理解其本质内涵却是很困难的。学生观察轴对称图形所得到的仅仅是一种感性认识，是一种朦胧的表象，是浮于表面的。因此在教学的第一阶段，笔者没有急功近利地给出轴对称图形的概念，而是引导学生联系生活，让他们去找寻生活中的同类物，以更好地积累关于轴对称图形的感性素材。这样的过程，可以为学生提炼规律、凝练概念，形成轴对称图形的数学模型打下坚实的基础。

[⇩] 二、在操作中感悟轴对称

实践是学生数学学习的重要手段，也是他们获得灵感、形成感悟的重要途径。为此，在学生初步感知轴对称图形的基础上，教师还需要引导学生进行必要的操作实践，让他们在操作中获得更深刻的体验，得到更深层次的感悟，进而更科学地理解轴对称图形的基本要义，建构良好的轴对称图形的几何直观表象。

师：你们观察得都很仔细，分析也很透彻。在数学上我们把这样的图形称为轴对称图形。结合刚才的观察、分析、交流等，你对轴对称图形有什么样的认识？

生1：我认为轴对称图形是一个可以重合的图形。

生2：你的说法我理解不了，什么是可以重合的图形啊！应该说是两部分是一模一样的图形。

生3：我认为应该是一条直线把图形分成两部分，这两部分是一模一样的。

……

师：噢！看来意见很难统一。有没有办法来验证一番呢？

生4：可以用实验的方法。

师：对！那就按照屏幕上的提示要求去做个实验吧！看看能不能从中获得更好的感悟。

（投影显示：将印有蝴蝶、天坛、飞机的纸片对折，看看有什么发现。）

生1：我把蝴蝶对折后，发现对折后两边的形状是完全一样的。

生2：是的！天坛、飞机的纸片被对折后也能重叠，说明两部分是完全一样的。

生3：我们讨论后认为，像这样对折，图形能够变成两部分，并且是重叠的，那么它就是轴对称图形。

……

师：不错！看来大家都很喜欢操作实践，那就继续用材料袋中的材料去实验一番。

（学生用准备好的材料进行实验。）

生1：我们对折长方形，发现它两部分是能够重叠的，所以长方形是轴对称图形。

生2：正方形对折后也是能够重叠的，所以它也是轴对称图形。

生3：我们对折了两个三角形，发现有一个三角形是可以重叠的，那它就是轴对称图形。另一个三角形不能重叠，它不是轴对称图形。

……

操作实践与交流反思是学生学习和掌握轴对称图形概念的基本手段，也是他们初步学习用数学的眼光看生活、看世界的机会。为此，笔者利用问题引导学生分两步去探究轴对称图形概念的本质，一是利用教材中的主题图，以纸片对折后所产生的折痕以及折痕两边完全相同的图案为素材，为学生进一步提炼概念积累直观认知;二是利用其他实践材料，让学生再度去实践、去观察、去思考，进一步把握重合、折痕等对称概念。我们有理由相信，当学生经历了一系列的操作实践与交流反思后，一定能感悟出轴对称图形的基本要素，也能够初步理解轴对称图形的实质。

[⇩] 三、在创作中深化轴对称

要使学生能够更好地认识轴对称图形，教师还需要设计相关的探究学习活动，以帮助他们更好地理解重合、对称轴等概念以及轴对称的本质。具体来说，教师可以设计诸如折纸剪出轴对称图形、在方格纸上画出轴对称图形的对称轴以及补全轴对称图形的另一半等学习创作活动，最终实现对轴对称图形学习的升华和对轴对称图形知识的有效建构。

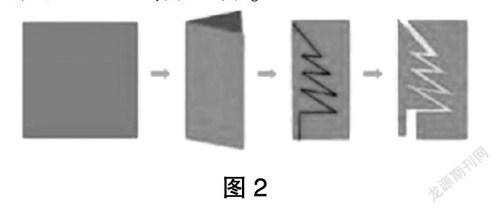
师（屏幕展示剪纸过程）：下面我们一起来做一做，看谁剪出的图案最棒。

（学生按照屏幕上的步骤进行剪纸活动。）

生1：我得出的是一个漂亮的松树。

……

师：不错，你们还能自己创作出一个属于自己的剪纸图案吗？

（学生运用课前准备好的彩纸进行剪纸活动。）

生2：我剪出了一个同心圆，它将4个圆组合在一起。

生3：我剪的是一个双喜图，很喜庆。

生4：我剪的是一个五角星图案。

生5：我剪出了一个美丽的雪花图形。

……

师：通过这些剪纸活动，你有哪些感悟？

生1：需要先将纸对折，再沿着对折的边缘画出图形的一半，剪下后就是一个完整的图形了。

生2：折纸很重要，这个折痕就是轴对称图形的对称轴。

……

对轴对称图形的认识以及对对称轴的理解，是学生学习的重点，也是难点。为此，笔者通过引导学生进行创作剪纸等相关活动，让学生在具体的操作实践中更好地感悟轴对称图形的重合性，理解对称轴的意义与价值。这样的活动，不仅提高了学生的动手能力和审美意识，还能引导学生自觉地联系中国的建筑、绘画、诗歌、书法等文化传承，从中体味对称美的独特韵味。

综上所述，在轴对称图形的相关教学活动中，把抽象的轴对称图形的学习与学生的生活相连接，能让学生在熟悉的情境中去思考，能让探究学习活动充满乐趣和挑战，也能让数学课堂变得更加生動。因此，教师还应该注重引导学生去观察生活中的种种现象，让他们在生活中发现数学知识，让他们的数学素养得到有效发展。