数学建模在中学数学教学中的实例研究

陆羿辰 金龚逸 徐张洋 胡江胜 张小华

摘 要：本文以2021年全国大学生数学建模竞赛A题为背景，对赛题进行适当改造，得到面向中学生的有限元点阵生成问题，并运用中学向量知识建立有限元点阵模型，通过二元线性不等式组的知识设计算法对模型求解，解决了一类在任意凸多边形中生成有限元点阵的问题。这一从本科生数学建模竞赛中提取素材、适当改编并使用中学数学知识求解问题的方法，为数学建模思想在中学数学教学中的渗透提供一种具有实践意义的教学思路。

关键词：数学建模;教学案例;向量;不等式组;有限元算法

自《普通高中数学课程标准（2017年版）》[1]颁布以来，数学建模作为一种重要的数学核心素养得到了广泛的研究。其中，如何将这一核心素养的培养融入中学教学成为一个重要的教学课题[2]。在之前的工作中，研究者已对数学建模的内涵与课堂实践进行了深入探讨。譬如，刘丹[3]从“北京市机动车保有量情况”这一现实问题出发，结合中学“函数的应用”知识在中学课堂中进行数学建模的教学，这也是大部分中学教师采用的教学方式。特别是，王志俊等[4]提出数学建模素材可以从大学生数学建模竞赛中提取的观点，这开辟了建模素材研究的新途径。但值得注意的是，大学生数学建模竞赛赛题的知识背景远超过中学生的认知水平。譬如，中学生虽然已经学习过函数与导数的相关知识，但是未接触过微分方程的相关知识。类似地，中学生学习过简单的线性规划，但是对于整数规划等较为复杂的规划问题却未曾接触。可见，照搬竞赛赛题无益于提高中学生数学建模能力，但是笔者认为如果对赛题加以改造，这将对中学生建模能力的培养大有裨益。在本文中笔者以2021年的全国大学生数学建模竞赛A题的部分题目为例，通过适当改造赛题，得到一类在中学知识背景下切实可行的建立与求解数学模型的方法，旨在为数学建模思想在中学数学教学中的渗透提供一种思路。

1 问题的背景与提出

2021年全国大学生数学建模竞赛A题为“FAST”主动反射面的形状调节，图1为“FAST”索网的反射面板及其连接示意图，其中主索网由柔性主索按照短程三角网格方式构成，每个三角网格上安装一块反射面板，与索网形状一致为三角形。

在赛题的问题3中，提出馈源舱有效接受比的概念，即馈源舱有效区域接收到的反射信号与300米口径内反射面的反射信号之比。由于反射面板、馈源舱接收平面、信号之间不存在共面、共线的几何关系，因此直接将空间几何图形视为主体来计算信号传输与反射情况较为复杂。相对简单的方案是，以有限元算法的视角，将光线在整个面板上的反射抽象为在光线在面板上有限个点的反射，并以馈源舱接收到反射信号的反射点个数与300米口径内反射点个数的比代替原先定义的有效接受比。根据有限元理论，点间的距离越短，点的划分越细密，以有限元估计的有效接受比与实际的接受比将越接近。

根据上述背景，提出以下问题：（1）假设已知空间中一块三角形反射面板各顶点的坐标，建立数学模型描述三角形面板上不同区域的坐标;（2）提供一种算法，要求算法能够由三角形的顶点坐标为已知量，生成三角形面板上一部分点的坐标，并且生成的点在三角形平面上是均匀的。

2.3 模型的求解

观察式（7）我们可以发现该限制条件为一组二元一次不等式组。在人教版高中数学必修五中，介绍了简单二元一次不等式组与简单线性规划问题，这里可以将高中数学教学内容中线性代数的内容和数学建模思想结合起来，设计一种求解算法。

根据以上算法，可生成给定精度下，三角形中所有有限元点的坐标。

3 总结与推广

上文介绍了基于向量与不等式组建立的有限元点阵模型的建立与求解过程。其中，有限元算法是一种在求解时将整个问题区域进行分解，求解每个子区域的部分问题最终加总求得整个问题区域近似解的数值技术。对于有限元算法，由于还未在高中教材中完整体现，本文希望对中学生起到兴趣培养与启蒙作用。在解题过程方面，通过初等数学知识来建立并求解数学模型来解决复杂现实问题的思想方法，对教师的教学以及学生的学习思维方式都起到重要作用，关键在于其背后数学建模思想的渗透。例如，通过结合中学生数学基础知识，对本科生数学建模竞赛赛题做适当修改，能够帮助教师更好地在中学数学教学中渗透数学建模思想，同时，中学生在思考并解决这类新型数学建模问题时，能够积累起数学知识在现实生活中应用的先验知识，提高学习数学的兴趣。

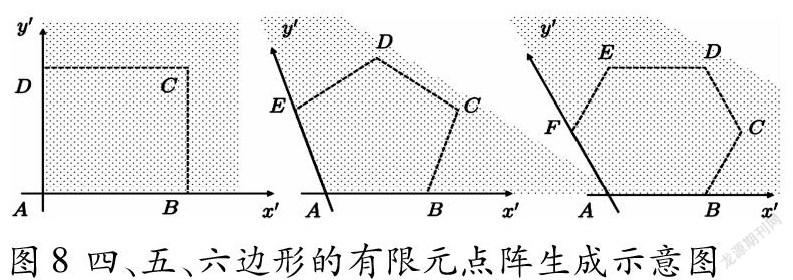
此外，文章中选取的多边形为三角形，如果跳出题设给定的框架，以求解任意凸多边形的有限元点阵为目标，模型是否仍然適用？答案是肯定的，如图8所示，我们仍然能以多边形的一对邻边上尾部相接的一对向量作为基向量，将其余边所在直线方程转化为不等式方程作为限制条件，求解多边形内的有限元点阵。由此也说明，模型具有较好的普适性，充分体现数学建模中“以某一数学模型解决一类实际问题”的思想。

综上所述，本文以2021年全国大学生数学建模竞赛A题中的一个问题为出发点，运用中学向量知识建立有限元点阵模型，并通过二元不等式组知识设计一种算法用于求解，解决了一类在任意凸多边形中生成有限元点阵的问题，提供了将复杂的几何关系化为若干简单问题逐一求解的解题思路，并体现了实际问题抽象化、一个模型解决一类问题的数学建模思想。此外，过程中运用了高等数学中有限元、线性代数的思想，对中学生起到了兴趣培养和启蒙作用，为数学建模思想在中学数学教育中的渗透提供一种具有实践意义的教学思路。

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版）[M].北京：人民教育出版社，2020.

[2]郑叶群.如何把高中数学建模核心素养渗透于课堂教学[J].教育现代化，2019，6（23）：253-254.

[3]刘丹.数学建模在高中数学课堂教学中的实践——以《函数的应用》为例[J].数学通报，2018，57（04）：36-39.

[4]王志俊，韩苗，邵虎，周圣武.高中数学建模能力训练——案例教学中提升数学素养[J].数学通报，2019，58（09）：38-42.

[5]章建跃.利用几何图形建立直观通过代数运算刻画规律——“平面向量及其应用”内容分析与教学思考[J].数学通报，2020，59（12）：4-13+29.

[6]章建跃，李增沪.普通高中教科书 数学 选择性必修 第二册 A版[M].北京：人民教育出版社，2019.

基金项目：国家自然科学基金（编号：12171206）;江苏省大学生创新创业训练计划项目（编号：202111463075Y）;江苏理工学院校级教改课题（编号：11611212050）;江苏省高等教育教改课题（编号：2021JSJG623）

作者简介：陆羿辰，男，江苏苏州人，江苏理工学院数理学院19级本科生，主要从事量化分析研究工作。

*通讯作者：胡江胜。